数学建模实验答案_概率模型
- 格式:doc
- 大小:2.07 MB
- 文档页数:27




P594•学校共1002名学生,237人住在A 宿舍,333人住在B 宿舍,432 人住在C 宿舍。
学生要组织一个10人的委员会,使用Q 值法分配各 宿舍的委员数。
解:设P 表示人数,N 表示要分配的总席位数。
i 表示各个宿舍(分别取 A,B,C ), p i 表 示i 宿舍现有住宿人数, n i 表示i 宿舍分配到的委员席位。
首先,我们先按比例分配委员席位。
23710 A 宿舍为:n A ==2.365 1002 333"0 B 宿舍为:n B =3.323 1002 432X0 C 宿舍为:n C =4.3111002现已分完9人,剩1人用Q 值法分配。
经比较可得,最后一席位应分给 A 宿舍。
所以,总的席位分配应为: A 宿舍3个席位,B 宿舍3个席位,C 宿舍4个席位。
QA23722 3= 9361.5 Q B33323 4 = 9240.7 Q C4322 4 5=9331.2商人们怎样安全过河傻麴删舫紬削< I 11山名畝臥蹄峨颂禮训鋤嫌邂 韻靖甘讹岸讎鞍輯毗匍趾曲展 縣確牡GH 錚俩軸飙奸比臥鋪謎 smm 彌鯉械即第紘麵觎岸締熾 x^M 曲颁M 删牘HX …佛讪卜过樹蘇 卜允棘髒合 岡仇卅毘冋如;冋冋1卯;砰=口 於广歎煙船上觸人敦% V O J U;xMmm朗“…他1曲策D 咿川| thPl,2卜允隸策集合 刼為和啊母紳轉 多步贱 就匚叫=1入“山使曲并按 腿翻律由汩3』和騒側),模型求解 -穷举法〜编程上机 ■图解法S={(x ?jOI x=o, j-0,1,2,3;X =3? J =0,1,2,3; X =»*=1,2}J规格化方法,易于推广考虑4名商人各带一随从的情况状态$=(xy¥)~ 16个格点 允许状态〜U )个。
点 , 允许决策〜移动1或2格; k 奇)左下移;&偶,右上移. 右,…,必I 给出安全渡河方案评注和思考[廿rfn片,rfl12 3xmm賤縣臓由上题可求:4个商人,4个随从安全过河的方案。
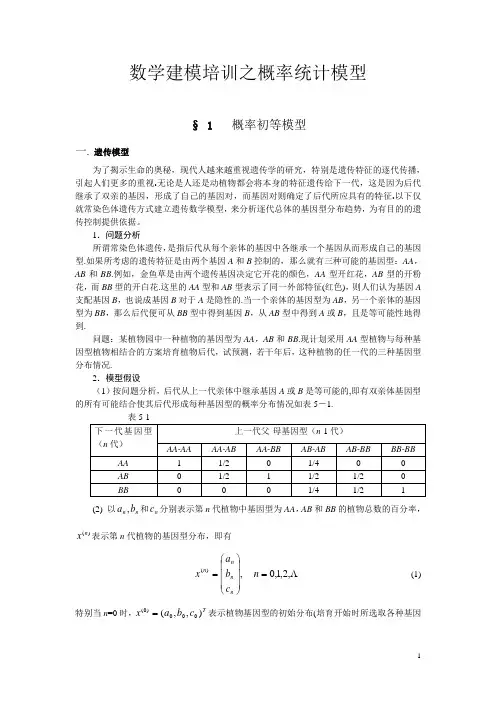
数学建模培训之概率统计模型§ 1 概率初等模型一. 遗传模型为了揭示生命的奥秘,现代人越来越重视遗传学的研究,特别是遗传特征的逐代传播,引起人们更多的重视.无论是人还是动植物都会将本身的特征遗传给下一代,这是因为后代继承了双亲的基因,形成了自己的基因对,而基因对则确定了后代所应具有的特征.以下仅就常染色体遗传方式建立遗传数学模型,来分析逐代总体的基因型分布趋势,为有目的的遗传控制提供依据。
1.问题分析所谓常染色体遗传,是指后代从每个亲体的基因中各继承一个基因从而形成自己的基因型.如果所考虑的遗传特征是由两个基因A 和B 控制的,那么就有三种可能的基因型:AA ,AB 和BB .例如,金鱼草是由两个遗传基因决定它开花的颜色,AA 型开红花,AB 型的开粉花,而BB 型的开白花.这里的AA 型和AB 型表示了同一外部特征(红色),则人们认为基因A 支配基因B ,也说成基因B 对于A 是隐性的.当一个亲体的基因型为AB ,另一个亲体的基因型为BB ,那么后代便可从BB 型中得到基因B ,从AB 型中得到A 或B ,且是等可能性地得到.问题:某植物园中一种植物的基因型为AA ,AB 和BB .现计划采用AA 型植物与每种基因型植物相结合的方案培育植物后代,试预测,若干年后,这种植物的任一代的三种基因型分布情况.2.模型假设 (1)按问题分析,后代从上一代亲体中继承基因A 或B 是等可能的,即有双亲体基因型的所有可能结合使其后代形成每种基因型的概率分布情况如表5-1.表5-1(2) 以n n b a ,和n c 分别表示第n 代植物中基因型为AA ,AB 和BB 的植物总数的百分率,)(n x 表示第n 代植物的基因型分布,即有,)(⎪⎪⎪⎭⎫⎝⎛=n n n n c b a x ,2,1,0=n (1) 特别当n =0时,T c b a x ),,(000)0(=表示植物基因型的初始分布(培育开始时所选取各种基因型分布),显然有.1000=++c b a3.模型建立注意到原问题是采用AA 型与每种基因型相结合,因此这里只考虑遗传分布表的前三列. 首先考虑第n 代中的AA 型,按上表所给数据,第n 代AA 型所占百分率为1110211---⋅+⋅+⋅=n n n n c b a a 即第n-1代的AA 与AA 型结合全部进入第n 代的AA 型,第n -1代的AB 型与AA 型结合只有一半进入第n 代AA 型,第n -1代的BB 型与AA 型结合没有一个成为AA 型而进入第n 代AA 型,故有1121--+=n n n b a a (2)同理,第n 代的AB 型和BB 型所占有比率分别为1121--+=n n n c b b (3)0=n c (4)将(2)、(3)、(4) 式联立,并用矩阵形式表示,得到,)1()(-=n n Mx x),2,1( =n (5)其中⎪⎪⎪⎭⎫ ⎝⎛=00012/1002/11M利用(5)进行递推,便可获得第n 代基因型分布的数学模型)0()2(2)1()(x M x M Mx x n n n n ====-- (6)(6)式明确表示了历代基因型分布均可由初始分布)0(x与矩阵M 确定.4.模型求解这里的关键是计算nM .为计算简便,将M 对角化,即求出可逆阵P ,使Λ=-MP P 1,即有1-Λ=P P M从而可计算 1-Λ=P P M nn),2,1( =n其中Λ为对角阵,其对角元素为M 的特征值,P 为M 的特征值所对应的特征向量.分别为,11=λ 212=λ,03=λ⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎭⎫ ⎝⎛=121,011,001321p p p故有1100210111,0211-=⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎪⎭⎫ ⎝⎛=ΛP P即得⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--=1002101110211100210111nnM ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=--00021210211211111n n n n 于是 ⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛=--00011)(000212102112111c b a c b a x n nn nn n n n或写为⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=--=--0)21()21()21()21(1010010n n n n n n nc c b b c b a 由上式可见,当∞→n 时,有0,0,1→→→n n n c b a即当繁殖代数很大时,所培育出的植物基本上呈现的是AA 型,AB 型的极少,BB 型不存在.5.模型分析(1)完全类似地,可以选用AB 型和BB 型植物与每一个其它基因型植物相结合从而给出类似的结果.特别是将具有相同基因植物相结合,并利用前表的第1、4、6列数据使用类似模型及解法而得到以下结果:000021,0,,21b c c b b a a n n n +→→+→这就是说,如果用基因型相同的植物培育后代,在极限情形下,后代仅具有基因AA 与BB ,而AB 消失了.(2)本例巧妙地利用了矩阵来表示概率分布,从而充分利用特征值与特征向量,通过对角化方法解决了矩阵n 次幂的计算问题,可算得上高等代数方法应用于解决实际的一个范例.二. 传送系统的效率模型1.问题的提出在机械化生产车间里你可以看到这样的情景:排列整齐的工作台旁工人们紧张地生产同一种产品,工作台上方一条传送带在运转,带上设置着若干钩子,工人们将产品挂在经过他上方的钩子上带走,如图1.当生产进入稳定状态后,每个工人生产出一件产品所需时间是不变的,而他要挂产品的时刻却是随机的.衡量这种传送系统的效率可以看它能否及时地把工人们生产的产品带走,显然在工人数目不变的情况下传送带速度越快,带上钩子越多,效率会越高.我们要构造一个衡量传送系统效率的指标,并且在一些简化假设下建立一个模型来描述这个指标与工人数目、钩子数量等参数的关系.2.问题的分析进入稳态后为保证生产系统的周期性运转,应假定工人们的生产周期相同,即每人作完一件产品后,要么恰有空钩经过他的工作台,使他可将产品挂上运走,要么没有空钩经过,迫使他放下这件产品并立即投入下件产品的生产。



(0349)《数学建模》网上作业题及答案1:第一批次2:第二批次3:第三批次4:第四批次5:第五批次6:第六批次1:[填空题]名词解释13.符号模型14.直观模型15.物理模型16.计算机模拟17.蛛网模型18.群体决策参考答案:13.符号模型:是在一定约束条件或假设下借助于专门的符号、线条等,按一定形式组合起来描述原型。
14.直观模型:指那些供展览用的实物模型以及玩具、照片等,通常是把原型的尺寸按比例缩小或放大,主要追求外观上的逼真。
15.物理模型:主要指科技工作者为一定的目的根据相似原理构造的模型,它不仅可以显示原型的外形或某些特征,而且可以用来进行模拟实验,间接地研究原型的某些规律。
16.计算机模拟:根据实际系统或过程的特性,按照一定的数学规律用计算机程序语言模拟实际运行情况,并依据大量模拟结构对系统或过程进行定量分析。
17.蛛网模型:用需求曲线和供应曲线分析市场经济稳定性的图示法在经济学中称为蛛网模型。
18.群体决策:根据若干人对某些对象的决策结果,综合出这个群体的决策结果的过程称为群体决策。
2:[填空题]名词解释7.直觉8.灵感9.想象力10.洞察力11.类比法12.思维模型参考答案:13.符号模型:是在一定约束条件或假设下借助于专门的符号、线条等,按一定形式组合起来描述原型。
14.直观模型:指那些供展览用的实物模型以及玩具、照片等,通常是把原型的尺寸按比例缩小或放大,主要追求外观上的逼真。
15.物理模型:主要指科技工作者为一定的目的根据相似原理构造的模型,它不仅可以显示原型的外形或某些特征,而且可以用来进行模拟实验,间接地研究原型的某些规律。
16.计算机模拟:根据实际系统或过程的特性,按照一定的数学规律用计算机程序语言模拟实际运行情况,并依据大量模拟结构对系统或过程进行定量分析。
17.蛛网模型:用需求曲线和供应曲线分析市场经济稳定性的图示法在经济学中称为蛛网模型。
18.群体决策:根据若干人对某些对象的决策结果,综合出这个群体的决策结果的过程称为群体决策。



第一部分课后习题1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。
学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:(1)按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者。
(2)节中的Q值方法。
(3)d’Hondt方法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,其商数如下表:将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A,B,C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位。
你能解释这种方法的道理吗。
如果委员会从10人增至15人,用以上3种方法再分配名额。
将3种方法两次分配的结果列表比较。
(4)你能提出其他的方法吗。
用你的方法分配上面的名额。
2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。
比如洁银牙膏50g装的每支元,120g装的元,二者单位重量的价格比是:1。
试用比例方法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。
价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。
(2)给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w的增加c减少的程度变小。
解释实际意义是什么。
3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数4.用宽w的布条缠绕直径d的圆形管道,要求布条不重叠,问布条与管道轴线的夹角 应多大(如图)。
若知道管道长度,需用多长布条(可考虑两端的影响)。
如果管道是其他形状呢。
5.用已知尺寸的矩形板材加工半径一定的圆盘,给出几种简便、有效的排列方法,使加工出尽可能多的圆盘。
实验10 概率模型(2学时)(第9章 概率模型)1.(验证)报童的诀窍p302~304, 323(习题2)关于每天报纸购进量的优化模型:已知b 为每份报纸的购进价,a 为零售价,c 为退回价(a > b > c ),每天报纸的需求量为r 份的概率是f (r )(r =0,1,2,…)。
求每天购进量n 份,使日平均收入,即1()[()()()]()()()nr r n G n a b r b c n r f r a b nf r ∞==+=----+-∑∑达到最大。
视r 为连续变量,f (r )转化为概率密度函数p (r ),则所求n *满足*()n a bp r dr a c-=-⎰已知b =0.75, a =1, c =0.6,r 服从均值μ=500(份),均方差σ=50(份)的正态分布。
报童每天应购进多少份报纸才能使平均收入最高,这个最高收入是多少?[提示:normpdf, normcdf]要求:(1) 在同一图形窗口内绘制10()()ny n p r dr =⎰和2()a by n a c-=-的图形,观察其交点。
[提示] 22()2()r p r μσ--=,0()()()n np r dr p r dr p r dr -∞-∞=-⎰⎰⎰☆(1) 运行程序并给出结果:(2) 求方程0()na bp r dr a c-=-⎰的根n *(四舍五入取整),并求G (n *)。
mu=500;sigma=50;a=1; b=0.75; c=0.6;r=n+1;while (a-b)*n*normpdf(r,mu,sigma)>1e-6r=r+1;endr=n+1:r;G=sum((a-b)*n*normpdf(r,mu,sigma));r=0:n;G=G+sum(((a-b)*r-(b-c)*(n-r)).*normpdf(r,mu,sigma))☆(2) 运行程序并给出结果:2.(编程)轧钢中的浪费p307~310设要轧制长l =2.0m的成品钢材,由粗轧设备等因素决定的粗轧冷却后钢材长度的均方差σ=0.2m,问这时钢材长度的均值m应调整到多少使浪费最少。
平均每得到一根成品材所需钢材的长度为()()mJ mP m=其中,22()2()(), ()2x mlP m p x dx p xσπσ--∞==⎰求m使J(m)达到最小。
等价于求方程()()zzzλϕΦ=-的根z*。
其中:()z Φ是标准正态变量的分布函数,即 ()()zz y dy ϕ∞Φ=⎰()z ϕ是标准正态变量的概率密度函数,即22()z z ϕ-=*,,*z l m mlz σσμσλμλ-=⇒==-=(1) 绘制J (m )的图形(l =2, σ=0.2),观察其最小值的位置。
★(1) 给出程序和运行结果:(2) 求使J (m )达到最小值的m *。
由(1)可观察到J(m)达到最小值的区间。
分别用求无约束最小值的MATLAB 函数fminbnd, fminsearch, fminunc 求解,并比较结果。
★(2) 给出程序及运行结果(比较[310]):(3) 在同一图形窗口内绘制1()()()z y z z ϕΦ=和2()y z z λ=-的图形,观察它们的交点。
(参考题1的(1))★(3) 给出程序及运行结果(比较[309]图2):z=-2:0.1:2;y1=(1-normcdf(z,0,1))./normpdf(z,0,1); l=2; sigma=0.2;(4)求方程()()zzzλϕΦ=-的根z*,并求m=l-σz*。
(参考题1的(2))提示:由(3)得到的图形可观察到z*的大概位置。
★(4) 给出程序及运行结果(比较[310]):3.(验证)航空公司的预订票策略p313~316模型如下:给定λ, n , p , b /g ,求m 使单位费用获得的平均利润J (m ) 最大。
∑--=---+-=11])()/1([1)(n m k k p n k m g b qm n m J λ约束条件为 1()(01)m n j j k k P m p αα---==≤<<∑其中:m 预订票数量的限额。
λ( < 1 ) 利润调节因子。
n 飞机容量。
p 每位乘客不按时前来登机的概率,q = 1 – p 。
b 每位被挤掉者获得的赔偿金。
g 机票价格。
b /g 赔偿金占机票价格的比例。
不按时前来登机的乘客数K 服从二项分布,其概率为p q p q p C k K P p k m k km k -=≤≤===-1,10,)(被挤掉的乘客数超过j 人的概率为∑---==1)(j n m k kj pm P(等价于m 位预订票的乘客中不按时前来登机的不超过m – n – j – 1人)该模型无法解析地求解,我们设定几组数据,用程序作数值计算。
[提示:binopdf, binocdf]要求:(1)已知n=300,λ=0.6,p=0.05,b/g=0.2和0.4,取一组值m=300:2:330,求出对应的J(m)、P5(m)和P10(m),程序如下。
(与教材p315表1 n=300时的计q=1-p; k=0:m-n-1;y=1/(lambda*n) *(q*m-(1+b_g)*sum((m-k-n).*binopdf(k,m,p)))-1;☆(1) 运行程序并给出结果(比较[315]表1(n=300)):(2)对(1)中改变p=0.1和m=300:2:344,求对应的结果。
☆(2) 运行程序并给出结果(比较[315]表1(n=300)):(3)对(1)中改变n=150和m=150:2:170,求对应结果。
(与教材时的计算结果比较。
)(4)对(1)中改变n=150、m=150:2:176和p=0.1,求对应结果。
注意!结果与教材相差较大,原因待查。
4.(编程)航空公司的预订票策略(改进)p316~317 已知:第2类乘客(t 人)都按时前来登机。
第1类乘客(m – t 人)不按时前来登机的乘客数K 服从二项分布,其概率为p q p q p C k K P p k t m k k t m k -=≤≤===---1,10,)(被挤掉的第1类乘客数超过j 人的概率为∑---==10)(j n m k k j pm P (等价于预订的第1类乘客中不按时前来登机的不超过( m– t ) – ( n – t ) – j – 1人)单位费用获得的平均利润为∑--=---+------=101])()/1()1([])1([1)(n m k k p n k m g b t p qm t n m J ββλ要求:已知n=300, λ=0.6, p=0.05, b/g=0.2, β=0.75,t=100,取一组值m=300:2:330,求出对应的J(m)、P5(m)和P10(m)。
参考实验10.3的程序,编写解决本问题的程序。
★给出编写的程序和运行结果:%9.6 航空公司的预订票策略(改进)function main()clear; clc; format short g;n=300; m=(300:2:330)'; p=0.05; %修改的参数lambda=0.6; % λ值b_g=0.2;t=100; beta=0.75;J1=zeros(size(m));for i=1:length(m)J1(i)=J(m(i),n,lambda,p,b_g,t,beta);endP5=binocdf(m-n-5-1,m-t,p); %二项分布P10=binocdf(m-n-10-1,m-t,p);round(10000*[m,J1,P5,P10])/10000 %显示结果function y=J(m,n,lambda,p,b_g,t,beta) %均是标量q=1-p; k=0:m-n-1;y=1/(lambda*(n-(1-beta)*t))...*(q*m-(1-beta-p)*t-(1+b_g)*sum((m-k-n).*binopdf(k,m-t,p)))-1;附1:实验提示附2:第9章概率模型[302]9.2 报童的诀窍[304]****本节完****[307]9.4 轧钢中的浪费[309] 题2(3)答案[310] 题2(2)(4)答案****本节完****[313]9.6 航空公司的预订票策略[317]****本节完****。