模拟信号相位补偿设计

模拟信号的特点及计算公式引言。

在电子领域中，信号是指传递信息的载体，可以分为模拟信号和数字信号两种类型。

模拟信号是一种连续变化的信号，它可以用连续的数学函数来描述。

本文将重点讨论模拟信号的特点及其计算公式。

一、模拟信号的特点。

1. 连续性。

模拟信号是连续变化的，它可以在任意时刻取到任意的值。

这意味着模拟信号可以在一个范围内无限细分，因此可以提供更加精细的信息。

2. 无限精度。

由于模拟信号是连续的，因此它的精度是无限的。

这意味着模拟信号可以表达任意精确的数值，而不受到数字信号离散化的限制。

3. 实时性。

模拟信号是实时变化的，它能够准确地反映出被测量对象的实时状态。

这使得模拟信号在一些需要及时响应的应用中具有优势，比如音频、视频等领域。

4. 受干扰影响大。

模拟信号在传输过程中容易受到外部干扰的影响，比如电磁干扰、噪声等。

这就需要在传输和处理过程中进行一定的干扰抑制和补偿。

二、模拟信号的计算公式。

在电子电路中，模拟信号可以用数学函数来描述。

下面将介绍一些常见的模拟信号计算公式。

1. 正弦信号。

正弦信号是一种最基本的模拟信号，它可以用以下数学函数来描述：\[x(t) = A \cdot sin(2\pi f t + \phi)\]其中，\(A\)代表振幅，\(f\)代表频率，\(\phi\)代表相位，\(t\)代表时间。

2. 方波信号。

方波信号是一种周期性的信号，它可以用以下数学函数来描述：\[x(t) = \frac{4A}{\pi} \sum_{n=1,3,5...}^{\infty} \frac{1}{n} sin(2\pi n f t)\]其中，\(A\)代表幅度，\(f\)代表频率，\(t\)代表时间。

3. 三角波信号。

三角波信号是一种周期性的信号，它可以用以下数学函数来描述：\[x(t) = \frac{8A}{\pi^2} \sum_{n=1,3,5...}^{\infty} \frac{(-1)^{\frac{n-1}{2}}}{n^2} sin(2\pi n f t)\]其中，\(A\)代表幅度，\(f\)代表频率，\(t\)代表时间。

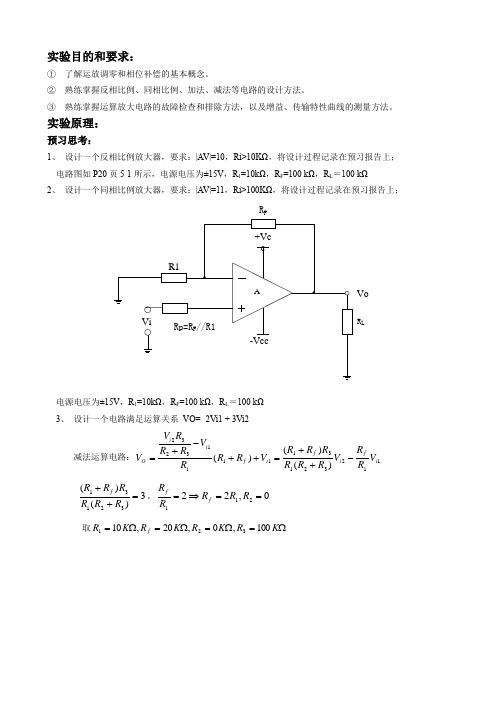
实验目的和要求：① 了解运放调零和相位补偿的基本概念。

② 熟练掌握反相比例、同相比例、加法、减法等电路的设计方法。

③ 熟练掌握运算放大电路的故障检查和排除方法，以及增益、传输特性曲线的测量方法。

实验原理：预习思考：1、 设计一个反相比例放大器，要求：|A V|=10，Ri>10KΩ，将设计过程记录在预习报告上； 电路图如P20页5-1所示，电源电压为±15V ，R 1=10kΩ，R F =100 kΩ，R L ＝100 kΩ2、 设计一个同相比例放大器，要求：|A V|=11，Ri>100KΩ，将设计过程记录在预习报告上；R F R LVo电源电压为±15V ，R 1=10kΩ，R F =100 kΩ，R L ＝100 kΩ 3、 设计一个电路满足运算关系 VO= -2Vi1 + 3Vi2减法运算电路：1123213111113232)()()(i f i f i f i i O V R R V R R R R R R V R R R V R R R V V -++=++-+=3)()(32131=++R R R R R R f ，0,22211==⇒=R R R R R f f取Ω=Ω=Ω=Ω=K R K R K R K R f 100,0,20,10321实验电路如实验内容：1、反相输入比例运算电路（I ） 按图连接电路，其中电源电压为±15V ，R 1=10 kΩ, R F =100 kΩ, R L =100 kΩ, R P =10 kΩ//100 kΩAR1R F Rp=R F //R1R LVoVi+Vcc-Vcc输入端接地，用万用表测量并记录输出端电压值，此时测出失调电压0.016 V 分析：失调电压是直流电压，将会直接影响直流放大器的放大精度。

直流信号测量：Vi/V V O /V Avf测量值 理论值 -2 14.25 -7.125 -10 -0.5 4.98 -9.96 -10 0.5 -5.02 -10.04 -10 2-12.87-6.435-10实验结果分析：运算放大器的输出电压摆幅受器件特性的限制，当输入直流信号较大时，经过运放放大后的输出电压如果超过V OM ，则只能输出V OM 的值。

《模拟集成电路设计》课程教学大纲一、课程基本信息1、课程编码：2、课程名称（中/英文）：模拟集成电路设计/ Design of Analog integrated Circuits3、学时/学分：56学时/3.5学分4、先修课程：电路基础、信号与系统、半导体物理与器件、微电子制造工艺5、开课单位：微电子学院6、开课学期（春/秋/春、秋）：秋7、课程类别：专业核心课程8、课程简介（中/英文）：本课程为微电子专业的必修课，专业核心课程，是集成电路设计方向最核心的专业课程之一。

本课程主要介绍典型模拟CMOS集成电路的工作原理、设计方法和设计流程、仿真分析方法，以及模拟CMOS集成电路的最新研发动态。

通过该课程的学习，将为学生今后从事集成电路设计奠定坚实的理论基础。

9、教材及教学参考书：教材：《模拟集成电路设计》，魏廷存，等编著教学参考书：1）《模拟CMOS集成电路设计》（第2版）.2）《CMOS模拟集成电路设计》二、课程教学目标本课程为微电子专业的必修课，专业核心课程，是集成电路设计方向最核心的专业课程之一。

通过该课程的学习，将为学生今后从事集成电路设计奠定坚实的理论基础。

本课程主要介绍典型模拟CMOS集成电路的工作原理、设计方法和设计流程、仿真分析方法，以及模拟CMOS模拟集成电路的最新研发动态。

主要内容有：1）模拟CMOS集成电路的发展历史及趋势、功能及应用领域、设计流程以及仿真分析方法；2）CMOS元器件的工作原理及其各种等效数学模型（低频、高频、噪声等）；3）针对典型模拟电路模块，包括电流镜、各种单级放大器、运算放大器、比较器、基准电压与电流产生电路、时钟信号产生电路、ADC与DAC电路等，重点介绍其工作原理、性能分析（直流/交流/瞬态/噪声/鲁棒性等特性分析）和仿真方法以及电路设计方法；4）介绍模拟CMOS集成电路设计领域的最新研究成果，包括低功耗、低噪声、低电压模拟CMOS集成电路设计技术。

二维FFT变换中的相位补偿作者：陈琛来源：《电子世界》2013年第17期【摘要】Fourier变换自Cooley和Tukey1965年提出了计算离散傅里叶变换的快速算法后，广泛应用于物理学、数论、信号处理，天线测量等领域。

目前有很多工具软件都可以快速实现FFT（Fast Fourier Transform），如FFTW，matlab等。

但目前通用的分析工具都是FFT 实现内核，没有明确模拟信号采集时位置初值对FFT变换结果相位补偿的影响。

当应用场景对相位信息敏感时，就必须考虑相位的影响。

本文以二维Fourier变换为例，从模拟信号采样出发，推导DFT、FFT过程中的相位补偿因子，并用仿真实例进行验证。

本文为弥补商业软件分析的不足及完整的Fourier分析提供一定的借鉴。

【关键词】FFT；傅里叶变换；相位补偿1.引言自Cooley和Tukey提出DFT快速实现算法以来，FFT广泛引用于信号处理、光学、通信和天线测量领域。

目前通用科学计算软件均支持FFT分析功能。

但在使用过程中发现这些分析软件只是针对数值序列的FFT分析，没有考虑实际模拟信号采集时的相位补偿作用。

在光学和天线测量领域，采样信号位置初值对FFT后信号相位影响巨大，不考虑相位补偿的影响则可能得出错误的结论。

本文将以二维Fourier变换为例从模拟信号出发，推导相位在FFT变换形式中的补偿因子，为后续完整FFT幅相分析提供一定的借鉴。

2.相位补偿因子的推导2.1 二维Fourier变换与逆变换4.结论本文推导了二维Fourier变换中采样初值对FFT的相位补偿作用。

给出了采样序列在经FFT变换后的相位补偿因子。

详细说明了FFT变换后自变量取值方式及fftshift的作用。

利用数值试验对推导结论进行了验证。

为克服目前商业分析工具的局限性及完整的FFT幅相分析提供一定的借鉴。

参考文献[1]Kamisetty Ramamohan Rao.快速傅里叶变换：算法与应用[M].机械工业出版社，2013（3）.[2]丁玉美.数字信号处理（第二版）[M].西安电子科技大学出版社，1994（6）.[3]程佩青.数字信号处理教程[M].清华大学出版社，2008（5）.[4]周建兴.MATLAB从入门到精通[M].人民邮电出版社，2008（11）.[5]王彬.MATLAB数字信号处理[M].机械工业出版社，2010（6）.。

相位补偿董晓勇一．为什么要相位补偿？当一个电路系统处于稳态后，其拉普拉斯变换因子s 就等于jω，那么电路的传输方程就可以用以s 为自变量的函数来表示。

一个稳定的电路系统往往是带有负反馈的，那么这样的电路其增益为(1)()()()()s A s k s A s A O O +=1上式中为放大器在低频下的开环增益，k （s ）是反馈系数，由于反馈网络往往不()s A O 是纯电阻网络，因此它也是一个复数。

这里假设了电路开环增益为正，假如电路是反相放大器，开环增益为，那么式1()s A 0−中不能简单地把用代替。

实际的增益应为，原因在于这()s A O ()s A O −()()()()s A s k s A s A O O +−=1时负反馈系数是一个负数，体现在电路上最典型可见课本上利用运算放大器实现的同相和反相放大器，前者是串联负反馈，后者是并联负反馈，一下的讨论全部基于同相放大器。

可见当在某个角频率s0处时，放大器的闭环增益将为无穷大。

虽然()()100−=s A s k O 这个角频率s0往往会远离于工作频段，如在音频放大器里s0>>20KHz ，但是在放大器开机瞬间，输入是一个阶跃信号，其频谱含量十分丰富，微小的角频率为s0的信号也会在电路中不断放大，从而产生自激振荡，放大器再无法正常工作。

那么当什么情况下会导致上述情况呢？我在之前的一篇文章里讲到：某个节点与其他的节点之间的关系呈纯电阻或纯电抗（如果是阻抗元件，则经过阻抗换算后，仍旧符合下面的说法），那么提供给整个电路的一个极点，且角频率为该点处时间常数的倒数。

而该点的时间常数则等于从该点看到交流地的等效电容与从该点看到交流地的等效电阻的乘积。

这样看来每个等效电容引入一个极点，那么当电路中三个电容形成闭合环路时是否引入了三个极点呢？答案是否定的。

其中的道理就在于密勒效应。

如图1所示，连接任意两个端口之间的一个阻抗元件可以看作是两个分别接地的阻抗元件。

BUCK 电路的环路计算，补偿和仿真Xia Jun 2010-8-14 本示例从简单的BUCK 电路入手，详细说明了如何进行电源环路的计算和补偿，并通过saber 仿真验证环路补偿的合理性。

一直以来，环路的计算和补偿都是开关电源领域的“难点”，很多做开关电源研发的工程师要么对环路一无所知，要么是朦朦胧胧，在产品的开发过程中，通过简单的调试来确定环路补偿参数。

而这种在实验室里调试出来的参数真的能满足各种实际的使用情况吗？能保证电源产品在高低温的情况下，在各种负载条件下，环路都能够稳定吗？能保证在负载跳变的情况下收敛吗？太多的未知数，这是产品开发的大忌。

我们必须明明白白的知道，环路的稳定性如何？相位裕量是多少？增益裕量是多少？高低温情况下这些值又会如何变化？在一些对动态要求非常严格的场合，我们如何折中考虑环路稳定性和动态响应之间的关系？有的放矢，通过明确的计算和仿真，我们的产品设计才是科学的，合理的，可靠的。

我们的目标是让产品经得起市场的检验，让客户满意，让自己放心。

一切从闭环系统的稳定性说起，在自动控制理论中，根据乃奎斯特环路稳定性判据，如果负反馈系统在穿越频率点的相移为180°，那么整个闭环系统是不稳定的。

很多人可能对这句话很难理解，虽然自动控制理论几乎是所有大学工科学生的必修课，可大部分是是抱着应付的态度的，学完就忘了。

那就再给大家讲解一下吧。

等式：V out=[Vin-V out*H(S)]*G(S)公式：Vout Vin G S ()1G S ()H S ()⋅+G(S)/(1+G(S)*H(S))就称之为系统的闭环传递函数，如果1+G(S)*H(S)=0，那么闭环系统的输出值将会无限大，此时闭环系统是不收敛的，也即是不稳定的。

G(S)*H(S)是系统的开环传递函数，当G(S)*H(S)=-1时，以S=j ω带入，即获得开环系统的频域响应为G(j ω)*H(j ω)=-1，此时频率响应的增益和相角分别为：gain =‖-1‖=1angle=tan -1(0/-1)=180°从上面的分析可以看出，如果扰动信号经过G(S)和H(S)后，模不变，相位改变180°，那么这个闭环系统就是不稳定的。

模拟电路设计中常见的失真问题分析
在模拟电路设计过程中，失真是一个非常常见的问题，影响着电路的性能和稳
定性。

失真可以由多种因素导致，包括元件的非线性特性、频率响应、温度变化等。

了解常见的失真问题有助于工程师更好地设计和优化模拟电路。

一、非线性失真
非线性失真是模拟电路设计中最常见的失真类型之一。

它通常由线性器件在工
作时产生的非线性效应引起。

例如，晶体管的饱和和截止效应、二极管的非线性特性等都会导致非线性失真。

这种失真会使信号失真、波形发生变形，严重影响电路的性能。

解决非线性失真问题的方法包括选择合适的线性器件、进行偏置电路的精确设计、采用负反馈技术等。

二、频率响应失真
频率响应失真是指电路在不同频率下的增益和相位特性发生变化，导致信号失
真和畸变。

频率响应失真通常由于电容、电感等元件的频率特性引起。

在设计时，需要注意电路的频率衰减、带宽等参数，以确保电路在整个频率范围内具有良好的性能。

采用频率补偿技术、增加滤波器等方法可以降低频率响应失真。

三、温度漂移失真
温度漂移失真是由于电路元件在温度变化时参数发生变化而导致的信号失真。

温度漂移会引起电路的工作点偏移、增益变化等问题，影响电路的稳定性和可靠性。

降低温度漂移失真的方法包括选择温度稳定性好的元件、进行精确的温度补偿
设计等。

总之，模拟电路设计中常见的失真问题包括非线性失真、频率响应失真、温度漂移失真等，需要工程师根据具体情况采取相应的优化和修正措施，以确保电路的性能和稳定性达到设计要求。

通过正确的分析和处理失真问题，能够提高电路的性能和可靠性，确保其正常工作。

filter 相位补偿在信号处理、通信和控制等领域，滤波器的设计与实现起着至关重要的作用。

然而，在实际应用中，滤波器往往面临这样一个问题：由于不同频率信号通过滤波器时，其相位变化不同，导致滤波器输出信号的相位差异。

为了解决这一问题，相位补偿技术应运而生。

一、相位补偿的概念与作用相位补偿，顾名思义，就是对滤波器输入和输出信号的相位差进行补偿。

其目的是消除或减小滤波器传输特性中的相位失真，从而提高信号处理系统的性能。

相位补偿方法主要有两种：一种是基于数字信号处理（DSP）的相位补偿，另一种是基于模拟电路实现的相位补偿。

二、相位补偿的算法与应用1.基于DSP的相位补偿在数字信号处理领域，相位补偿算法主要有以下几种：（1）延时法：通过调整信号处理单元的输入延时，使得滤波器输出信号的相位与参考信号的相位保持一致。

（2）数字滤波法：通过对输入信号进行数字滤波，改变信号的相位特性，实现相位补偿。

（3）插值法：在时域或频域对信号进行插值处理，以达到相位补偿的目的。

2.基于模拟电路的相位补偿对于模拟电路实现的相位补偿，主要有以下几种方法：（1）电容耦合法：通过电容耦合器实现信号的相位调整。

（2）变压器耦合法：利用变压器的相位调整特性实现相位补偿。

（3）运算放大器法：通过运算放大器构建相位补偿电路，实现信号的相位调整。

三、相位补偿在滤波器设计中的应用在滤波器设计中，相位补偿技术可以有效改善滤波器的性能，提高系统的稳定性。

具体应用如下：1.在多径信道环境下，通过相位补偿技术，可以降低滤波器的group delay 失真，提高信号的传输质量。

2.对于高通、低通、带通等不同类型的滤波器，相位补偿技术可以有效调整滤波器的频率响应，满足不同应用场景的需求。

3.在多通道滤波器设计中，相位补偿技术可以减小各通道之间的相位差异，降低系统的复杂性。

四、相位补偿在实际工程中的案例分析1.无线通信系统：在无线通信系统中，多径效应会导致信号的相位差异。

filter 相位补偿摘要：1.相位补偿的概念与作用2.相位补偿的原理与应用3.相位补偿在滤波器设计中的重要性4.如何实现相位补偿5.相位补偿技术的未来发展正文：在信号处理领域，滤波器设计是一项关键任务，而相位补偿则是实现高性能滤波器的关键环节。

本文将从相位补偿的概念、原理、应用以及如何在滤波器设计中实现相位补偿等方面进行详细阐述。

一、相位补偿的概念与作用相位补偿是指在信号传输过程中，对信号的相位进行调整，以消除或减小信号传输过程中的相位失真。

相位补偿技术在通信、音频、视频等领域具有广泛的应用，它能有效提高信号质量，改善系统性能。

二、相位补偿的原理与应用相位补偿的原理是基于信号传输过程中的相位变化规律。

当信号经过不同媒介传输时，其速度和传播特性会发生改变，导致信号相位的改变。

为了消除这种相位失真，需要在信号传输链路中加入相位补偿器，对信号相位进行调整。

相位补偿技术在许多领域都有应用，如光纤通信、射频通信、音频处理等。

在滤波器设计中，相位补偿技术能够提高滤波器的性能，实现更好的频率响应和群延迟特性。

三、相位补偿在滤波器设计中的重要性在滤波器设计中，相位补偿技术具有重要作用。

滤波器的主要性能指标包括频率响应、群延迟、相位响应等。

相位补偿能够调整滤波器的相位响应，使其在特定频率下具有更好的性能。

此外，相位补偿还能改善滤波器之间的相互影响，提高整个滤波器系统的性能。

四、如何实现相位补偿实现相位补偿的方法有很多，如使用相位调整器、插入相位补偿器等。

在滤波器设计中，常用的相位补偿方法包括：1.使用模拟滤波器：通过调整模拟滤波器的系数，实现对信号相位的补偿。

2.使用数字滤波器：在数字信号处理中，通过编程实现数字滤波器的相位补偿。

3.采用级联滤波器：通过级联多个滤波器，实现对信号相位的逐步调整。

五、相位补偿技术的未来发展随着科技的不断发展，相位补偿技术也将不断创新。

在未来，相位补偿技术将更加高效、精确，满足更多领域的应用需求。

dpd相位补偿相位补偿是数字通信系统中常用的一种技术，用于消除信号传输中产生的相位偏移，以确保数据传输的准确性和可靠性。

下面将就相位补偿的原理、分类和应用进行详细讨论。

相位补偿的原理主要涉及到相位偏移的度量和调整。

在数字通信系统中，数据的传输是通过将模拟信号转换为数字信号进行，而数字信号在传输过程中可能会受到各种干扰和衰减，导致传输时的信号与原始信号存在相位偏移。

相位偏移会导致接收端无法正确识别和解码原始信号，从而影响通信质量。

因此，相位补偿的关键目标就是恢复信号的原始相位，以确保数据传输的准确性。

相位补偿技术可以分为两类：主动相位补偿和自适应相位补偿。

主动相位补偿是指在通信系统中添加额外的设备或模块来实现相位的精确调整。

常见的主动相位补偿方法有数字锁相环（DLL）和相位锁定循环（PLL）。

DLL通过频率摄取器和数字延迟线实现相位调整，能够快速跟踪输入信号的频率和相位变化，适用于高速数据传输系统。

PLL则通过相位检测器和VCO实现相位调整，具有更高的稳定性和抗噪声性能，适用于要求较高的通信系统。

自适应相位补偿是指根据信号的特性和传输环境的变化自动调整相位补偿的方法。

自适应相位补偿可以根据接收到的信号特征动态地调整补偿值，在实际应用中更加灵活和智能。

其中，常见的自适应相位补偿算法有最小均方误差（MMSE）算法和时域决策反馈（TDF）算法。

MMSE算法通过最小化接收信号与原始信号之间的均方误差来计算相位补偿值，能够有效地提高系统的传输性能。

TDF算法根据接收到的信号中的冗余信息和噪声等因素来自动调整相位补偿值，适用于多采样率（MSR）系统和自适应速率系统等工作环境。

相位补偿技术在许多应用领域得到广泛应用，特别是在高速数据传输、无线通信和光纤通信等领域。

在高速数据传输中，相位补偿可以有效地消除时钟抖动和信号失真等问题，提高数据传输速率和可靠性。

在无线通信中，相位补偿可以提高接收机对传输信号的抗干扰性和抗衰减性能，实现更远距离的沟通。

多路射频信号相位同步模块的设计与实现王宁【摘要】相控阵短波发信系统是提高短波通信效率、保持通信方向实时控制的有效途径之一.天线阵的波束控制是通过对馈电天线的射频信号相位进行补偿实现的.为了满足该发信系统在空间波束合成过程中相位可控的要求,设计和实现了相位同步模块.该模块采用基于DSP和FPGA协作配合的软硬件平台的相位检测技术,能够对射频信号进行相位补偿.经过系统的实测实验数据验证,该模块能够实现多路射频信号的相位同步,且移相精确,控制方便.【期刊名称】《通信技术》【年(卷),期】2018(051)006【总页数】4页(P1487-1490)【关键词】相控阵;相位同步;短波通信;波束合成【作者】王宁【作者单位】91336部队,河北秦皇岛 066000【正文语种】中文【中图分类】TN9140 引言相控阵技术是控制阵列天线各阵元的相位以形成空间波束并控制其扫描的技术，最早在20世纪50年代应用于雷达领域[1-3]。

相控阵短波发信系统采用相控阵技术的原理，目标是通过波束控制的手段实现空间功率的合成，提高短波发信系统的效能和通信业务控制的实时性，实现通信方向能够根据通信对象要求随时可控的效果，使天线的布置灵活机动、按需可控，从而满足短波通信系统全方位、远距离的要求[3]。

近年来，随着技术的发展，相控阵技术由于突出的优势在短波通信中的运用越来越广泛。

本文针对相控阵技术的关键点相位校正设计了具体方案，并且通过实际测量验证了本系统的可靠性。

1 系统简介相控阵短波发信系统的基础是波束合成技术，即通过改变一组天线阵中的每个单元天线激励信号的相位，实现波束合成功率的最大化[4-5]。

实现波束合成的基础是在馈入相位前保证射频信号相位的同步性。

天线阵的相位同步是通过闭环系统中对射频信号进行相位检测，从而补偿相位，采用数字信号处理技术有效解决各通道射频单元产生的“随机”相位，即数字上变频时各数字载波初始相位和D/A转换时钟相位的不一致引起的射频相位差，实现多路信号的精确相位同步。