1离散试题A

贵州大学软件学院软件工程专业2018-2019学年第二学期考试试卷A离散数学注意事项：1. 请考生按要求在试卷装订线内填写姓名、学号和年级专业。

2. 请仔细阅读各种题目的回答要求，在规定的位置填写答案。

3. 不要在试卷上乱写乱画，不要在装订线内填写无关的内容。

4. 满分100分，考试时间为120分钟。

题 号一 二 三 四 总分 统分人得 分一．单项选择题（每小题2分，共20分）1. p ：小王学习用功，q ：小王聪明，则命题“小王不仅学习用功而且聪明.”的符号化为（ ）。

A ．p →qB ．q →pC ．p ∨qD ．p ∧ q2．n 个命题变元可产生（ ）个互不等价的极小项。

A ． nB ． n 2C ． 2nD ． 2n3．设个体域为整数集,下列公式中假命题的有（ ）。

A ．x ∃y(x ·y=0)B ．∃x y(x ·y=0)C ．x ∃y(x ·y=1)D ．x ∃y(x ·y=x)4. 集合A={1,2,3}上的关系R={<1,2>,<1,3>}，则R 的性质为（ ）。

A.自反的B.对称的C.传递的，对称的D.传递的5. 若,f g 是双射，则复合函数g f 必是（ ）。

A ．映射B ．单射C ．满射D ．双射6．给定下列序列，可构成无向简单图的结点度数序列的是（ ）。

A ．(1,1,2,2,5)B ．(1,1,2,2,2)C ．(1,1,3,3,3)D ．(1,5,4,4,5)得 分评分人7. 给定无向图如下图所示，割点是（ ）。

A ．dB ．gC ．bD ． a8. 7阶连通平面图G 有6个面，则G 的边数为（ ）。

A ．9B ．10C ．11D ．129. 无向图G 是简单图，则图G 中一定不含有（ ）。

A ．环和平行边B ．平行边C ．环D ．圈10. Z 是整数集，〈Z ，*〉（其中*是普通乘法）不能构成（ ）。

离散数学试题（A 卷答案）一、（10分）求(P ↓Q )→(P ∧⌝(Q ∨⌝R ))的主析取范式 解：(P ↓Q )→(P ∧⌝(Q ∨⌝R ))⇔⌝(⌝( P ∨Q ))∨(P ∧⌝Q ∧R ))⇔(P ∨Q )∨(P ∧⌝Q ∧R ))⇔(P ∨Q ∨P )∧(P ∨Q ∨⌝Q )∧(P ∨Q ∨R ) ⇔(P ∨Q )∧(P ∨Q ∨R )⇔(P ∨Q ∨(R ∧⌝R ))∧(P ∨Q ∨R ) ⇔(P ∨Q ∨R )∧(P ∨Q ∨⌝R )∧(P ∨Q ∨R ) ⇔0M ∧1M⇔2m ∨3m ∨4m ∨5m ∨6m ∨7m二、（10分）在某次研讨会的休息时间，3名与会者根据王教授的口音分别作出下述判断： 甲说：王教授不是苏州人，是上海人。

乙说：王教授不是上海人，是苏州人。

丙说：王教授既不是上海人，也不是杭州人。

王教授听后说：你们3人中有一个全说对了，有一人全说错了，还有一个人对错各一半。

试判断王教授是哪里人？解 设设P ：王教授是苏州人；Q ：王教授是上海人；R ：王教授是杭州人。

则根据题意应有： 甲：⌝P ∧Q 乙：⌝Q ∧P 丙：⌝Q ∧⌝R王教授只可能是其中一个城市的人或者3个城市都不是。

所以，丙至少说对了一半。

因此，可得甲或乙必有一人全错了。

又因为，若甲全错了，则有⌝Q ∧P ，因此，乙全对。

同理，乙全错则甲全对。

所以丙必是一对一错。

故王教授的话符号化为：((⌝P ∧Q )∧((Q ∧⌝R )∨(⌝Q ∧R )))∨((⌝Q ∧P )∧(⌝Q ∧R ))⇔(⌝P ∧Q ∧Q ∧⌝R )∨(⌝P ∧Q ∧⌝Q ∧R )∨(⌝Q ∧P ∧⌝Q ∧R ) ⇔(⌝P ∧Q ∧⌝R )∨(P ∧⌝Q ∧R ) ⇔⌝P ∧Q ∧⌝R ⇔T因此，王教授是上海人。

三、（10分）证明tsr (R )是包含R 的且具有自反性、对称性和传递性的最小关系。

证明 设R 是非空集合A 上的二元关系，则由定理4.19知，tsr (R )是包含R 的且具有自反性、对称性和传递性的关系。

桂林电子科技大学试卷A学年第 学期 课号课程名称 离散数学（闭卷） 适用班级分钟 班级 学号 姓名考试时间 120一．单项选择题：（每小题2分，共12分）1．以下4个命题公式中，哪个是永真式？ （ ）A．p→(p→q)； B．(p→q)∨┓q→┓p；C．(p→q)∧┓q→┓p； D．┓(p↔┓p∨q)。

2．设P(x)表示“x在桂林上学”，Q(x)表示“x是桂林人”，则“在桂林上学的人未必是桂林人”可以表示为： （ ）A． x┓(P(x)→Q(x))； B．┓ x(P(x)→Q(x))；C． x(P(x)→┓Q(x))； D．┓ x(P(x)→┓Q(x))。

3．某个集合的元素个数为10，这个集合有多少个不同的子集？（ ）。

A．10； B．20； C．102； D．210。

4．设R为实数集，映射σ：R→R定义为σ(x)=2x－1，则σ是：（ ）A．单射而非满射； B．满射而非单射；C．双射； D．既不是单射，也不是满射。

5． 设R是实数集，C是复数集合，试问下列各个代数系统哪一个是交换群？（ ）A．<M（n×n；R），·>，其中M（n×n；R）是所有元素为实数的n×n 矩阵集，·是矩阵的普通乘法；B．<A，*>，其中A＝｛1，2，3，4，6，12｝，a*b为a与b的最大公约数，a，b∈A；C．<M（m×n；R），+>，其中M（m×n；R）是所有元素为实数的m×n矩阵集，+是矩阵的加法；D．<Z，+>，其中Z＝｛z|z∈C且z的实部为非负数｝，+是复数的加法。

6．给定有向图见下图，则其邻接矩阵是： （ ）V V 34A ．B ．C ．D ． 0 1 0 1 0 0 0 0 0 1 0 1 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 0 1 0 0 1 0 1 0 1 0 1 0 0 1 1 1 0 0 1 0 0 0 1 0 0二．填空题：（每个空2分，共16分）1．在谓词公式 x (∃w (P (x,w )∧P (x,y ))→(Q (x,y,z )∨Q (x,z,y )))中，约束变元为 ___________，自由变元为 __________。

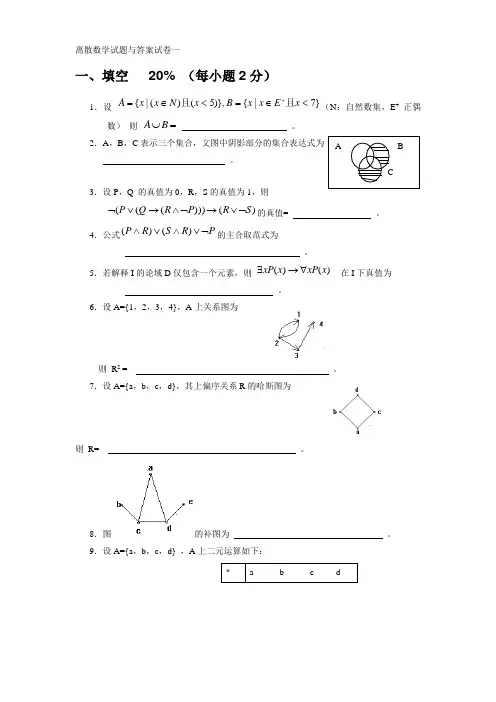
离散数学试题与答案试卷一一、填空 20% （每小题2分）1．设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且（N ：自然数集，E + 正偶数） 则 =⋃B A 。

2．A ，B ，C 表示三个集合，文图中阴影部分的集合表达式为 。

3．设P ，Q 的真值为0，R ，S 的真值为1，则 )()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。

4．公式P R S R P ⌝∨∧∨∧)()(的主合取范式为。

5．若解释I 的论域D 仅包含一个元素，则 )()(x xP x xP ∀→∃ 在I 下真值为。

6．设A={1，2，3，4}，A 上关系图为则 R 2 = 。

7．设A={a ，b ，c ，d}，其上偏序关系R 的哈斯图为则 R= 。

8．图的补图为 。

9．设A={a ，b ，c ，d} ，A 上二元运算如下：* a b c dA BCa b cda b c db c d ac d a bd a b c那么代数系统<A，*>的幺元是，有逆元的元素为，它们的逆元分别为。

10．下图所示的偏序集中，是格的为。

二、选择20% （每小题2分）1、下列是真命题的有（）A．}}{{}{aa⊆；B．}}{,{}}{{ΦΦ∈Φ；C．}},{{ΦΦ∈Φ；D．}}{{}{Φ∈Φ。

2、下列集合中相等的有（）A．{4，3}Φ⋃；B．{Φ，3，4}；C．{4，Φ，3，3}；D．{3，4}。

3、设A={1，2，3}，则A上的二元关系有（）个。

A．23 ；B．32 ；C．332⨯；D．223⨯。

4、设R，S是集合A上的关系，则下列说法正确的是（）A．若R，S 是自反的，则SR 是自反的；B．若R，S 是反自反的，则SR 是反自反的；C．若R，S 是对称的，则SR 是对称的；D．若R，S 是传递的，则SR 是传递的。

5、设A={1，2，3，4}，P（A）（A的幂集）上规定二元系如下|}||(|)(,|,{tsApt st sR=∧∈><=则P（A）/ R=（）A．A ；B．P(A) ；C．{{{1}}，{{1，2}}，{{1，2，3}}，{{1，2，3，4}}}；D．{{Φ}，{2}，{2，3}，{{2，3，4}}，{A}}6、设A={Φ，{1}，{1，3}，{1，2，3}}则A上包含关系“⊆”的哈斯图为（）7、下列函数是双射的为（）A．f : I→E , f (x) = 2x ；B．f : N→N⨯N, f (n) = <n , n+1> ；C．f : R→I , f (x) = [x] ；D．f :I→N, f (x) = | x | 。

离散数学考试题库（A卷及答案）一、（10分）证明⌝(A∨B)→⌝(P∨Q)，P，(B→A)∨⌝P A。

证明：(1)⌝(A∨B)→⌝(P∨Q)P(2)(P∨Q)→(A∨B) T(1)，E(3)P P(4)A∨B T(2)(3)，I(5)(B→A)∨⌝P P(6)B→A T(3)(5)，I(7)A∨⌝B T(6)，E(8)(A∨B)∧(A∨⌝B) T(4)(7)，I(9)A∧(B∨⌝B) T(8)，E(10)A T(9)，E二、（10分）甲、乙、丙、丁4个人有且仅有2个人参加围棋优胜比赛。

关于谁参加竞赛，下列4种判断都是正确的：(1)甲和乙只有一人参加；(2)丙参加，丁必参加；(3)乙或丁至多参加一人；(4)丁不参加，甲也不会参加。

请推出哪两个人参加了围棋比赛。

解符号化命题，设A：甲参加了比赛；B：乙参加了比赛；C：丙参加了比赛；D：丁参加了比赛。

依题意有，(1)甲和乙只有一人参加，符号化为A⊕B⇔(⌝A∧B)∨(A∧⌝B)；(2)丙参加，丁必参加，符号化为C→D；(3)乙或丁至多参加一人，符号化为⌝(B∧D)；(4)丁不参加，甲也不会参加，符号化为⌝D→⌝A。

所以原命题为：(A⊕B)∧(C→D)∧(⌝(B∧D))∧(⌝D→⌝A)⇔((⌝A∧B)∨(A∧⌝B))∧(⌝C∨D)∧(⌝B∨⌝D)∧(D∨⌝A)⇔((⌝A∧B∧⌝C)∨(A∧⌝B∧⌝C)∨(⌝A∧B∧D)∨(A∧⌝B∧D))∧((⌝B∧D)∨(⌝B∧⌝A)∨(⌝D∧⌝A))⇔(A∧⌝B∧⌝C∧D)∨(A∧⌝B∧D)∨(⌝A∧B∧⌝C∧⌝D)⇔T但依据题意条件，有且仅有两人参加竞赛，故⌝A∧B∧⌝C∧⌝D为F。

所以只有：(A∧⌝B∧⌝C∧D)∨(A∧⌝B∧D)⇔T，即甲、丁参加了围棋比赛。

三、（10分）指出下列推理中，在哪些步骤上有错误？为什么？给出正确的推理形式。

(1)∀x(P(x)→Q(x)) P(2)P(y)→Q(y) T(1)，US(3)∃xP(x) P(4)P(y) T(3)，ES(5)Q(y) T(2)(4)，I(6)∃xQ(x) T(5)，EG解(4)中ES错，因为对存在量词限制的变元x引用ES规则，只能将x换成某个个体常元c，而不能将其改为自由变元。

吉林大学软件学院2005级本科《离散数学I》试题（A）一、简答题（本大题共20小题，每小题2分，共40分）1、设集合A={∅}，则幂集合ρ(ρ(A))的基数是多少？2、设命题公式的集合S={P，Q，P∧Q，P∨Q}，⇒是S上的公式蕴涵关系，则部分序集(S, ⇒)中的最大元和最小元是什么？3、设集合A={a, b}，请给出集合A上所有的等价关系。

4、设R是集合A={1,2,3}上的二元关系，R={(1,1),(2,3),(3,1)}，问R满足反自反性吗？R满足反对称性吗？5、是否存在集合A，使得A与ρ(A)等势？若存在，请举例说明。

6、命题公式(P∧(⌝P→Q))→Q是恒真公式吗？若不是，请给出一个弄假G的解释。

7、写出关于3个原子P、Q、R的极小项m3。

8、若短语恒假，则该短语中一定包含互补对吗？若子句中包含互补对，则该子句一定恒真吗？9、对于包含4个不同原子的恒假公式，其主析取范式共包含多少个极小项？10、蕴含式∀xP(x)⇒∃xP(x)一定成立吗？11、设G＝∀xP(x)∨∀xQ(x)，H＝∀x(P(x)∨Q(x))，个体域D={a，b}，请给弄假公式G，但满足H的一个解释。

12、有向树中所有点都只发出一条弧吗？有向树一定强连通吗？13、没有孤立点的Euler图一定是强连通的吗？其中的Euler路一定经过图中每个点吗？14、若有限树T中共有m(m≥2)个度为1的点，则树T中任意点的度一定≤m，对吗？15、给出mod 9的一个完全剩余系和一个简化剩余系。

16、任意整数都能写成质数乘积吗？若不能，请举例。

17、若a|b且b|a，则a=b，对吗？18、对任意正整数m、n，都有n m≡n(mod m)成立吗？若不成立，请举反例。

19、对任意两个整数a、b的最高公因数d，都有d=sa+tb，s、t为整数，请问s和t的最高公因数是多少？20、画出右图的闭合图，在该图的闭合图中共有多少条不同的Hamilton回路？（注：若两条Hamilton回路包含的边完全相同(可能顺序不同)，则这两条Hamilton回路相同；两条不同的Hamilton回路中至少存在一条不同的边，）。

学年第二学期期末考试《离散数学》试卷（ A ）使用班级：命题教师：主任签字：一、单项选择题(本大题共15小题，每小题1分，共15分)在每小题列出的四个选项中只有一个选项是符合题目要求的，请将正确选项前的字母填在题后的括号内。

1.一个连通的无向图G，如果它的所有结点的度数都是偶数，那么它具有一条( )A.汉密尔顿回路B.欧拉回路C.汉密尔顿通路D.初级回路2.设G是连通简单平面图，G中有11个顶点5个面，则G中的边是( )A.10B.12C.16D.143.在布尔代数L中，表达式(a∧b)∨(a∧b∧c)∨(b∧c)的等价式是( )A.b∧(a∨c)B.(a∧b)∨(a’∧b)C.(a∨b)∧(a∨b∨c)∧(b∨c)D.(b∨c)∧(a∨c)4.设i是虚数，·是复数乘法运算，则G=<{1,-1,i,-i},·>是群，下列是G的子群是( )A.<{1},·>B.〈{-1},·〉C.〈{i},·〉D.〈{-i},·〉5.设Z为整数集，A为集合，A的幂集为P(A),+、-、/为数的加、减、除运算，∩为集合的交运算，下列系统中是代数系统的有( )A.〈Z，+，/〉B.〈Z，/〉C.〈Z，-，/〉D.〈P(A)，∩〉6.下列各代数系统中不含有零元素的是( )A.〈Q，*〉Q是全体有理数集，*是数的乘法运算B.〈Mn(R),*〉,Mn(R)是全体n阶实矩阵集合，*是矩阵乘法运算C.〈Z，ο〉，Z是整数集，ο定义为xοxy=xy,∀x,y∈ZD.〈Z，+〉，Z是整数集，+是数的加法运算7.设A={1,2,3}，A上二元关系R的关系图如下：R具有的性质是A.自反性B.对称性C.传递性D.反自反性8.设A={a,b,c}，A上二元关系R={〈a,a〉，〈b,b〉,〈a,c〉}，则关系R的对称闭包S(R)是( )A.R∪I AB.RC.R∪{〈c,a〉}D.R∩I A9.设X={a,b,c},Ix是X上恒等关系，要使Ix∪{〈a,b〉，〈b,c〉，〈c,a〉，〈b,a〉}∪R为X上的等价关系，R应取( )A.｛〈c,a〉，〈a,c〉｝B.{〈c,b〉，〈b,a〉}C.{〈c,a〉，〈b,a〉}D.{〈a,c〉，〈c,b〉}10.下列式子正确的是( )A. ∅∈∅B.∅⊆∅C.{∅}⊆∅D.{∅}∈∅11.设解释R如下：论域D为实数集，a=0,f(x,y)=x-y,A(x,y):x<y.下列公式在R下为真的是( )A.( ∀x)( ∀y)( ∀z)(A(x,y))→A(f(x,z),f(y,z))B.( ∀x)A(f(a,x),a)C.(∀x)(∀y)（A(f(x,y),x))D.(∀x)(∀y)(A(x,y)→A(f(x,a),a))12.设B是不含变元x的公式，谓词公式(∀x)(A(x)→B)等价于( )A.(∃x)A(x)→BB.(∀x)A(x)→BC.A(x)→BD.(∀x)A(x)→(∀x)B13.谓词公式(∀x)(P(x,y))→(∃z)Q(x,z)∧(∀y)R(x,y)中变元x( )A.是自由变元但不是约束变元B.既不是自由变元又不是约束变元C.既是自由变元又是约束变元D.是约束变元但不是自由变元14.若P：他聪明；Q：他用功；则“他虽聪明，但不用功”，可符号化为( )A.P∨QB.P∧┐QC.P→┐QD.P∨┐Q15.以下命题公式中，为永假式的是( )A.p→(p∨q∨r)B.(p→┐p)→┐pC.┐(q→q)∧pD.┐(q∨┐p)→(p∧┐p)二、填空题(每空1分，共20分)16.在一棵根树中，仅有一个结点的入度为______，称为树根，其余结点的入度均为______。

离散数学考试试题（A卷及答案）一、（10分）某项工作需要派A、B、C和D 4个人中的2个人去完成，按下面3个条件，有几种派法？如何派？(1)若A去，则C和D中要去1个人；(2)B和C不能都去；(3)若C去，则D留下。

解设A：A去工作；B：B去工作；C：C去工作；D：D去工作。

则根据题意应有：A→C⊕D，⌝(B ∧C)，C→⌝D必须同时成立。

因此(A→C⊕D)∧⌝(B∧C)∧(C→⌝D)⇔(⌝A∨(C∧⌝ D)∨(⌝C∧D))∧(⌝B∨⌝C)∧(⌝C∨⌝D)⇔(⌝A∨(C∧⌝ D)∨(⌝C∧D))∧((⌝B∧⌝C)∨(⌝B∧⌝D)∨⌝C∨(⌝C∧⌝D))⇔(⌝A∧⌝B∧⌝C)∨(⌝A∧⌝B∧⌝D)∨(⌝A∧⌝C)∨(⌝A∧⌝C∧⌝D)∨(C∧⌝ D∧⌝B∧⌝C)∨(C∧⌝ D∧⌝B∧⌝D)∨(C∧⌝ D∧⌝C)∨(C∧⌝ D∧⌝C∧⌝D)∨(⌝C∧D∧⌝B∧⌝C)∨(⌝C∧D∧⌝B∧⌝D)∨(⌝C∧D∧⌝C)∨(⌝C∧D∧⌝C∧⌝D)⇔F∨F∨(⌝A∧⌝C)∨F∨F∨(C∧⌝ D∧⌝B)∨F∨F∨(⌝C∧D∧⌝B)∨F∨(⌝C∧D)∨F⇔(⌝A∧⌝C)∨(⌝B∧C∧⌝ D)∨(⌝C∧D∧⌝B)∨(⌝C∧D)⇔(⌝A∧⌝C)∨(⌝B∧C∧⌝ D)∨(⌝C∧D)⇔T故有三种派法：B∧D，A∧C，A∧D。

二、（15分）在谓词逻辑中构造下面推理的证明：某学术会议的每个成员都是专家并且是工人，有些成员是青年人，所以，有些成员是青年专家。

解：论域：所有人的集合。

S(x)：x是专家；W(x)：x是工人；Y(x)：x是青年人；则推理化形式为：∀x(S(x)∧W(x))，∃x Y(x)∃x(S(x)∧Y(x))下面给出证明：(1)∃x Y(x) P(2)Y(c) T(1)，ES(3)∀x(S(x)∧W(x)) P(4)S( c)∧W( c) T(3)，US(5)S( c) T(4)，I(6)S( c)∧Y(c) T(2)(5)，I(7)∃x S((x)∧Y(x)) T(6) ，EG三、（10分）设A、B和C是三个集合，则A⊂B⇒⌝(B⊂A)。

离散数学考试试题(A 卷及答案)一、 (10 分)判断下列公式的类型(永真式、永假式、可满足式)？1)((P Q)∧Q)一 ((Q∨R)∧Q) 2)((Q P)∨P)∧ (P∨R)3)((P∨Q)R)((P∧Q)∨R)解： 1)永真式； 2) 永假式； 3)可满足式。

二、 (8 分) 个体域为{1， 2}，求x3y (x+y=4)的真值。

解：x3y (x+y=4) 一 x ((x+1=4)∨(x+2=4))一((1+1=4)∨(1+2=4))∧((2+1=4)∨(2+1=4))一(0∨0)∧(0∨1)一1∧1一0三、 (8 分) 已知集合 A 和 B 且|A|=n， |B|=m，求 A 到 B 的二元关系数是多少？ A 到 B 的函数数是多少？解：因为|P(A×B) |=2|A×B|=2|A| |B|=2mn，所以 A 到 B 的二元关系有 2mn 个。

因为|BA|= |B| |A|=mn，所以 A 到 B 的函数 mn 个。

四、 (10 分) 已知 A={1,2,3,4,5}和 R={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>}，求 r(R) 、s(R)和 t(R)。

解： r(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<1,1>,<2,2>,<3,3>,<4,4>,<5,5>} s(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<3,2>,<4,3>,<4,5>}t(R)={<1,2>,<2,1>,<2,3>,<3,4>,<5,4>,<1,1>,<1,3>,<2,2>,<2,4>,<1,4>}五、 (10 分) 75 个儿童到公园游乐场，他们在那里可以骑旋转木马，坐滑行铁道，乘宇宙飞船，已知其中20 人这三种东西都乘过，其中 55 人至少乘坐过其中的两种。

离散数学（A）卷讲解⼀、单项选择题(本⼤题共15⼩题，每⼩题1分，共15分)在每⼩题列出的四个选项中只有⼀个选项是符合题⽬要求的，请将正确选项前的字母填在题后的括号内。

1.⼀个连通的⽆向图G，如果它的所有结点的度数都是偶数，那么它具有⼀条( )A.汉密尔顿回路B.欧拉回路C.汉密尔顿通路D.初级回路2.设G是连通简单平⾯图，G中有11个顶点5个⾯，则G中的边是( )A.10B.12C.16D.143.在布尔代数L中，表达式(a∧b)∨(a∧b∧c)∨(b∧c)的等价式是( )A.b∧(a∨c)B.(a∧b)∨(a’∧b)C.(a∨b)∧(a∨b∨c)∧(b∨c)D.(b∨c)∧(a∨c)4.设i是虚数，?是复数乘法运算，则G=<{1,-1,i,-i},?>是群，下列是G的⼦群是( )A.<{1},?>B.〈{-1},?〉C.〈{i},?〉D.〈{-i},?〉5.设Z为整数集，A为集合，A的幂集为P(A),+、-、/为数的加、减、除运算，∩为集合的交运算，下列系统中是代数系统的有( )A.〈Z，+，/〉B.〈Z，/〉C.〈Z，-，/〉D.〈P(A)，∩〉6.下列各代数系统中不含有零元素的是( )A.〈Q，*〉Q是全体有理数集，*是数的乘法运算B.〈Mn(R),*〉,Mn(R)是全体n阶实矩阵集合，*是矩阵乘法运算C.〈Z，〉，Z是整数集，定义为∈ZD.〈Z，+〉，Z是整数集，+是数的加法运算7.设A={1,2,3}，A上⼆元关系R的关系图如下：R具有的性质是D.反⾃反性8.设A={a,b,c}，A上⼆元关系R={〈a,a〉，〈b,b〉,〈a,c〉}，则关系R的对称闭包S(R)是( )A.R∪IAB.RC.R∪{〈c,a〉}D.R∩IA9.设X={a,b,c},Ix是X上恒等关系，要使Ix∪{〈a,b〉，〈b,c〉，〈c,a〉，〈b,a〉}∪R为X上的等价关系，R应取( )A.｛〈c,a〉，〈a,c〉｝B.{〈c,b〉，〈b,a〉}C.{〈c,a〉，〈b,a〉}D.{〈a,c〉，〈c,b〉}10.下列式⼦正确的是( )A. ∈∈11.设解释R如下：论域D为实数集，a=0,f(x,y)=x-y,A(x,y):xA.( x)( y)( z)(A(x,y))→A(f(x,z),f(y,z))B.( x)A(f(a,x),a)C.( x)( y)（A(f(x,y),x))D.( x)( y)(A(x,y)→A(f(x,a),a))12.设B是不含变元x的公式，谓词公式( x)(A(x)→B)等价于( )A.( x)A(x)→BB.( x)A(x)→BC.A(x)→BD.( x)A(x)→( x)B13.谓词公式( x)(P(x,y))→( z)Q(x,z)∧( y)R(x,y)中变元x( )A.是⾃由变元但不是约束变元B.既不是⾃由变元⼜不是约束变元C.既是⾃由变元⼜是约束变元D.是约束变元但不是⾃由变元14.若P：他聪明；Q：他⽤功；则“他虽聪明，但不⽤功”，可符号化为( )D.P∨┐Q15.以下命题公式中，为永假式的是( )A.p→(p∨q∨r)B.(p→┐p)→┐pC.┐(q→q)∧pD.┐(q∨┐p)→(p∧┐p)⼆、填空题(每空1分，共20分)16.在⼀棵根树中，仅有⼀个结点的⼊度为______，称为树根，其余结点的⼊度均为______。

上海第二工业大学（试卷编号：）2012～2013学年第一学期离散数学A 卷姓名：学号：班级：成绩：一、判断题（每小题2分，本题共10分） 1、若A B A C =，则B C =。

( 错 ) 2、设1ρ和2ρ是集合A 上的等价关系，则12ρρ是A 上的等价关系( 对 )3、若函数:f A B →，:g B C →，则若f 与g 的复合gf 是双射，则函数f 是双射。

( 错 )4、在有界格中，必有最大元和最小元。

( 对 )5、存在13个结点，并且每个结点的度均为3的图。

( 错 )二、填空题(每空2分，本题30分) 1、设集合{,{}}A a b =，{,}B a b =，则22AB =_______{空，{a}}________________，B A ⨯=_________{(a,a),(b,a),(a,{b}),(b,{b}}________________。

2、若{1,2,3,4}A =，则A 上共有___11_______个不同的自反关系。

3、假设{0,1,2,3}A =，1{(,)|2}i j j i ρ==+和2{(,)|2}i j i j ρ==+是A 上的关系，则12ρρ=_____{(0,0),(1,1)}__；21ρρ=___{(2,2),(3,3)}；关系1ρ的自反闭包是：__{(0,0),(1,1),(2,2),(3,3),(0,2),(1,3)}__；关系2ρ的对称闭包是：_{(1,3),(3,1),(2,0),(0,2)}_。

4、命题P ：“小李喜欢跳舞”，命题Q ：“小李不喜欢唱歌”，则复合命题P Q ⌝∧表示：____小李不喜欢跳舞且不喜欢唱歌_____________________。

5、设集合{1,2,3,4}A =，{,,,}B a b c d =，则A B ⨯有___16__个序偶，A 到B 有___256____个关系，其中有____24____个是双射函数。

天津师范大学考试试卷2009 —2010 学年第一 学期期末考试试卷（A 卷）科目： 离散数学学院： 管理学院专业：08信管、物流一、 单项选择题:在每小题的备选答案中选出一个正确答案，并将正确答案的代（每小题2分，本大题共20分）1.下面说法中不正确的是（ ）。

A. 在命题逻辑中，任何命题公式的主合取范式都是存在的，并且是唯一的。

B. 在命题逻辑中，命题公式的等价关系具有自反，对称和传递性。

C. 非空集合A 上的恒等关系既是A 上的等价关系，也是A 上的偏序关系。

D. 非空集合A2. 设A={1,2,3,4,5}，下面（ ）集合等于A 。

A.{1,2,3,4}B.{x|x 是整数，且x 2≤25} C.{x|x 是正整数x ≤5} D.{x|x 3. 设A={1,2,4}，B={1,3,{2}}，下列各式成立的是（ ）。

A.{2}∈A B. {2}∈B C.{2}⊆B D. ∅∈A4. 已知集合A={a,b,c}，A 上的两个二元关系：R 1={<a,b >,<a,c >,<b,c >}，R 2={<a,b >,<a,a >}，则R 1◦R 2=（ ）。

A. ∅B. {<a,b >,<a,c >,<b,c >}C. {<a,b >,<a,c >}D. {<a,b >,<a,a5.公式()()()()y x Q y x P x ,∃→∀的前束范式为（ ）。

A. ()()()()()y x Q x P y x ,→∀∀ B. ()()()()()y u Q x P y x ,→∃∃ C. ()()()()()y x Q x P y x ,→∀∃ D. ()()()()()y x Q x P y x ,→∃∃6. 将命题“若m 是奇数，则2m 是偶数”符号化为（ ）。

济南大学继续教育学院离散数学试卷（A）学年：学期:年级：专业：学习形式：层次：（本试题满分100分，时间90分钟）一、选择（每题2分，共18分）1.设简单图G所有结点的度之和为12，则G一定有 ( ) 条边。

A． 3B． 4C． 5D． 62.设G是一棵树，则G 的生成树有 ( B ) 棵A． 0B． 1C． 2D．不能确定3. 若供选择答案中的数值表示一个简单图中各个顶点的度，能画出图的是( )。

A. (1,2,2,3,4,5)B. (1,2,3,4,5,5)C. (1,1,1,2,3)D. (2,3,3,4,5,6).4. 命题∀xG(x)取真值1的充分必要条件是( )。

A.对任意x，G(x)都取真值1.B.有一个x0，使G(x0)取真值1.C.有某些x，使G(x0)取真值1.D.以上答案都不对.5.设集合A={2,{a},3,4}，B = {{a},3,4,1}，E为全集，则下列命题正确的是( )。

A. {2}∈AB. {a}⊆AC. ∅⊆{{a}}⊆B⊆ED. {{a},1,3,4}⊂B.6. 下列关于集合的表示中正确的为( )。

A.{a}∈{a,b,c}B. {a}⊆{a,b,c}C. ∅∈{a,b,c}D. {a,b}∈{a,b,c}7.下列式子正确的是 ( )。

A． p →q = q →pB． p →q = ⌝q ∨ pC． p →q，q →s ⇒ p →sD． p ↔q = (p → q) ∨ (q→ p)8.下列语句中，( )是命题。

A.请把门关上B.地球外的星球上也有人C. x + 5 > 6D. 下午有会吗？9．设G、H是一阶逻辑公式，P是一个谓词，G＝∃xP(x), H＝∀xP(x),则一阶逻辑公式G→H是( )。

A. 恒真的第 1 页共 13 页。

离散数学试题A卷及答案一、单项选择题（每题2分，共10分）1. 在集合{1,2,3}中，子集的个数是多少？A. 3B. 7C. 8D. 9答案：C2. 以下哪个命题是真命题？A. ∃x∈R, x^2 = -1B. ∀x∈R, x^2 ≥ 0C. ∀x∈R, x^2 = 1D. ∃x∈R, x^2 = 2答案：B3. 函数f: N → N定义为f(x) = 2x，该函数是：A. 单射B. 满射C. 双射D. 非函数答案：A4. 以下哪个逻辑表达式等价于p∧(q∨¬p)？A. p∧qB. p∨qC. ¬p∨qD. p∧¬p答案：A5. 以下哪个图是二分图？A. 完全图K5B. 完全二分图K3,3C. 环图C5D. 星形图K1,4答案：B二、填空题（每题3分，共15分）1. 若A={1,2,3}，B={2,3,4}，则A∩B=______。

答案：{2,3}2. 命题“若x>0，则x^2>0”的逆否命题是：若x^2≤0，则______。

答案：x≤03. 在一个有向图中，若存在从顶点u到顶点v的有向路径，则称v可到达u，若图中每个顶点都可到达其他所有顶点，则称该有向图是______。

答案：强连通的4. 一个集合的幂集包含该集合的所有______。

答案：子集5. 在逻辑中，合取（AND）操作符用符号______表示。

答案：∧三、解答题（每题10分，共20分）1. 证明：若A⊆B且B⊆C，则A⊆C。

证明：设x∈A，则由A⊆B，可得x∈B。

又由B⊆C，可得x∈C。

因此，A⊆C。

2. 给定一个图G，包含顶点集V={v1, v2, v3, v4}和边集E={(v1,v2), (v2, v3), (v3, v4), (v4, v1), (v1, v3), (v2, v4)}，请判断该图是否是欧拉图，并说明理由。

答案：该图是欧拉图。

因为该图是连通的，且每个顶点的度都是偶数。

结束语：本试题涵盖了离散数学中的基本概念和原理，通过这些题目的练习，可以加深对离散数学知识的理解。

离散数学试题A6. 令F(x):x是⾦属，G(y):y是液体，H(x,y):x可以溶解在y中，则命题“任何⾦属可以溶解在某种液体中”可符号化为什么逻辑表达式。

（）A.(?x)(F(x)∧(?y)(G(y)∧H(x,y)))B.(?x)(?(x)F(x)→(G(y)→H(x,y)))C.(?x)(F(x)→(?y)(G(y)∧H(x,y)))D.(?x)(F(x)→(?y)(G(y)→H(x,y))7. 在个体域D={a,b}中，指出与公式(?x)A(x)等价⼜不含量词的公式。

（）A.A(a)∧A(b)B.A(a)→A(b)C.A(a)∨A(b)D.A(b)→A(a)8. 指出下列是命题的句⼦。

（）A.⽔开了吗?B.x>1.59. 给定算式: (((a＋(b＊c))＊d－e)÷(f＋g))－((h＊i)＊j)找出与此算式对应的波兰符号表⽰式。

（）A．－＊＊a＋bc＋def－g＊hij＊＊ B. abc＊＋d＊e－fg＋÷hi＊j＊－C．－÷－＊＋a＊bcde＋fg＊＊hij D. ab＋c＊de＋＊fgh＊－＋ij＊－10. 设N是⾃然数集，函数f: N→N×N. f(n)＝﹤n,n＋1﹥,f({5})是什么。

（）A．满射函数B．单射函数C．{<5,6>} D．双射函数11. 已知(p→q)←→r的主析取范式是m1∨m3∨m4∨m7，指出与其对应的主合取范式。

A．m1∨m2∨m5∨m7 B．M0∧M2∧M5∧M6 （）C．m0∧m3∧m5∧m6 D．M1∨M3∨M5∨M612. 设T(x)：x具有性质T，S(y)：y具有性质S。

命题“若存在x具有性质T，则所有的y都没有性质S“的符号化形式是什么。

（）A. ?x (T(x)→S(x))B. ?x (T(x)∧S(x))C. ?x T(x)→?y S(y)D. ?xT(x)→?y? S(y)13. 判断下列各⾮负整数列哪个不是可图化的。