一次函数的图象 第课时(优质课)获奖课件

精美获奖课件54《一次函数的图像》课件一、教学内容1. 一次函数的一般形式：y=kx+b（k≠0，k、b为常数）。

2. 一次函数的图像：一条穿过原点的直线，斜率为k，截距为b。

3. 一次函数的斜率：表示直线的倾斜程度，k>0时，直线向上倾斜；k<0时，直线向下倾斜。

4. 一次函数的截距：表示直线与y轴的交点，b>0时，直线在y轴上方；b<0时，直线在y轴下方。

5. 一次函数的图像与系数的关系：k>0时，图像在第二、四象限；k<0时，图像在第一、三象限；b>0时，图像在y轴上方；b<0时，图像在y轴下方。

二、教学目标1. 让学生掌握一次函数的一般形式，理解斜率和截距的概念及意义。

2. 培养学生利用一次函数的图像解决实际问题的能力。

3. 培养学生合作学习、积极探究的学习态度。

三、教学难点与重点1. 教学难点：一次函数图像的斜率和截距的求法及应用。

2. 教学重点：一次函数图像与系数的关系。

四、教具与学具准备1. 教具：黑板、粉笔、投影仪、电脑。

2. 学具：教材、练习册、三角板、直尺、彩笔。

五、教学过程1. 实践情景引入：利用投影仪展示生活中的一些实际问题，如购物、出行等，引导学生发现这些问题都可以用一次函数来表示。

2. 例题讲解：以教材第54页例1为例，讲解一次函数的图像特点及斜率和截距的求法。

3. 随堂练习：让学生独立完成教材第54页的练习题，教师巡回指导。

4. 小组讨论：让学生分小组讨论一次函数图像与系数的关系，引导学生发现规律。

6. 课堂小结：让学生复述本节课所学内容，检查学生对知识的掌握情况。

7. 布置作业：让学生完成教材第55页的课后作业。

六、板书设计1. 一次函数的一般形式：y=kx+b（k≠0，k、b为常数）。

2. 一次函数的图像：一条穿过原点的直线，斜率为k，截距为b。

3. 一次函数的斜率：表示直线的倾斜程度，k>0时，直线向上倾斜；k<0时，直线向下倾斜。

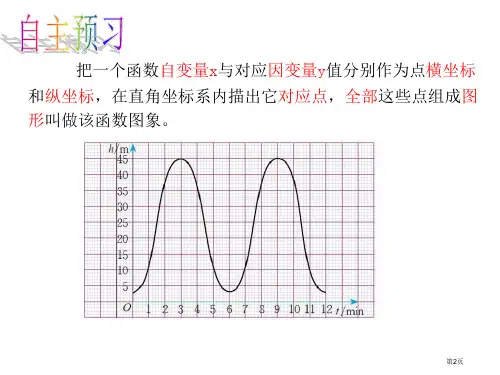
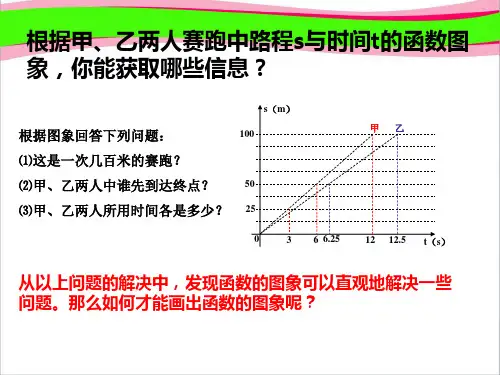
精美获奖课件54《一次函数的图像》课件一、教学内容本节课的内容为《一次函数的图像》，选自人教版八年级数学下册第十一章第一节。

详细内容包括：一次函数的定义、图像及其性质；一次函数图像的绘制方法；一次函数图像在实际问题中的应用。

二、教学目标1. 让学生掌握一次函数的定义、图像及其性质，能熟练绘制一次函数的图像。

2. 培养学生运用一次函数图像解决实际问题的能力，提高学生的数学思维。

3. 培养学生合作交流、动手实践的能力。

三、教学难点与重点教学难点：一次函数图像的绘制方法，一次函数图像在实际问题中的应用。

教学重点：一次函数的定义、图像及其性质。

四、教具与学具准备教具：多媒体课件、黑板、粉笔。

学具：直尺、圆规、量角器。

五、教学过程1. 导入：通过展示一次函数在实际生活中的应用实例，激发学生兴趣，引出本节课的主题。

2. 新课导入：（1）讲解一次函数的定义，引导学生理解并掌握。

（2）通过例题讲解，让学生学会一次函数图像的绘制方法。

3. 随堂练习：（1）让学生独立绘制一次函数的图像。

4. 应用拓展：（1）展示一次函数在实际问题中的应用，引导学生学会运用。

（2）分组讨论，让学生互相交流，提高解决问题的能力。

（1）让学生回顾本节课所学内容，加深对一次函数的认识。

六、板书设计1. 定义：一次函数的定义。

2. 图像：一次函数的图像及其性质。

3. 绘制方法：一次函数图像的绘制方法。

4. 应用：一次函数在实际问题中的应用。

七、作业设计1. 作业题目：情境一：小明骑自行车去学校，速度为4km/h，行驶1小时后，距离学校还有6km。

情境二：小华买了一个玩具车，原价100元，每过一年，价值降低10元。

2. 答案：（1）略。

（2）情境一：y = 4x + 10；情境二：y = 10x + 100。

八、课后反思及拓展延伸1. 反思：本节课学生对一次函数的定义和图像绘制方法掌握较好，但在实际问题中的应用还需加强。

2. 拓展延伸：（1）引导学生探究一次函数图像的平移、伸缩变换。

精美获奖课件54《一次函数的图像》课件一、教学内容本节课选自教材第七章第三节，详细内容为一次函数的图像。

通过本章学习，学生将掌握一次函数图像的特点、绘制方法及其在实际问题中的应用。

二、教学目标1. 知识与技能：使学生掌握一次函数图像的斜率、截距及其关系，能够独立绘制一次函数的图像。

2. 过程与方法：培养学生运用数形结合的思想分析问题、解决问题的能力。

3. 情感态度与价值观：激发学生学习数学的兴趣，提高学生的观察能力、动手操作能力和团队协作能力。

三、教学难点与重点重点：一次函数图像的斜率、截距及其关系。

难点：一次函数图像的绘制方法及其在实际问题中的应用。

四、教具与学具准备1. 教具：多媒体课件、黑板、粉笔。

2. 学具：直尺、圆规、量角器、铅笔、橡皮。

五、教学过程1. 导入：通过实际情景引入，展示一次函数在生活中的应用，激发学生学习兴趣。

教师活动：展示一组图片，如直线上升的气温、斜率表示速度等，引导学生观察并思考一次函数在生活中的应用。

学生活动：观察图片，思考一次函数在生活中的应用。

2. 新课导入：引导学生回顾一次函数的定义，为新课的学习做好铺垫。

教师活动：提问学生一次函数的定义，引导学生复习相关知识。

学生活动：回答问题，复习一次函数的定义。

3. 知识讲解：（1）介绍一次函数图像的斜率、截距及其关系。

教师活动：通过课件展示，讲解斜率、截距的定义及其关系。

学生活动：认真听讲，理解斜率、截距的概念。

（2）讲解一次函数图像的绘制方法。

教师活动：通过例题讲解，展示一次函数图像的绘制方法。

学生活动：跟随教师思路，学习绘制一次函数图像。

4. 随堂练习：教师活动：布置一道练习题，让学生独立完成。

学生活动：运用所学知识，完成练习题。

5. 小组讨论：教师活动：提出问题，引导学生分组讨论。

学生活动：分组讨论，共同解决问题。

六、板书设计1. 一次函数的图像2. 内容：（1）斜率、截距的定义及关系（2）一次函数图像的绘制方法（3）一次函数图像在实际问题中的应用七、作业设计1. 作业题目：（1）绘制y=2x+1的图像，并求出斜率和截距。

精美获奖课件54《一次函数的图像》课件一、教学内容本节课选自教材第十五章《一次函数及其图像》的第一节，详细内容包括一次函数的定义、图像特征及其应用。

着重讲解一次函数y=kx+b（k≠0）的图像性质，如何通过斜率k和截距b判断一次函数的增减性，以及一次函数在实际问题中的应用。

二、教学目标1. 让学生掌握一次函数的定义，理解其图像的直线特征。

2. 使学生能够通过斜率k和截距b判断一次函数的增减性，并运用到实际问题中。

3. 培养学生的观察能力、动手能力和逻辑思维能力。

三、教学难点与重点教学难点：一次函数图像的增减性判断。

教学重点：一次函数的定义、图像特征及其应用。

四、教具与学具准备教具：多媒体课件、黑板、粉笔。

学具：直尺、圆规、计算器。

五、教学过程1. 实践情景引入（5分钟）通过展示一次函数在现实生活中的应用实例，如气温变化、物体运动等，引导学生感受一次函数与生活的密切联系。

2. 知识讲解（15分钟）（1）讲解一次函数的定义，让学生明确一次函数的形式和特点。

（3）讲解斜率k和截距b的含义，引导学生判断一次函数的增减性。

3. 例题讲解（10分钟）选取具有代表性的例题，详细讲解解题思路和步骤，强调一次函数图像的增减性判断。

4. 随堂练习（10分钟）布置随堂练习题，让学生运用所学知识解决问题，巩固课堂所学。

六、板书设计1. 一次函数的定义2. 一次函数图像的特征3. 斜率k和截距b的含义及判断方法4. 例题解析5. 随堂练习题七、作业设计1. 作业题目：（1）已知一次函数y=2x+3，求该函数图像的斜率和截距。

2. 答案：（1）斜率为2，截距为3。

（2）y=3x+4为减函数，y=5x2为增函数。

八、课后反思及拓展延伸1. 是否有针对性地解决学生的疑问和困惑。

2. 是否充分调动学生的学习积极性，提高课堂参与度。

3. 课后拓展延伸：引导学生思考一次函数在现实生活中的其他应用，如股票走势、人口增长等。

让学生将所学知识运用到实际问题中，提高解决问题的能力。

精美获奖课件54《一次函数的图像》课件一、教学内容本节课选自教材《数学》七年级下册第十一章第一节“一次函数的图像”。

详细内容包括：一次函数的定义，一次函数图像的特点，如何绘制一次函数的图像，并学会通过图像分析一次函数的性质。

二、教学目标1. 理解并掌握一次函数的定义，能够识别一次函数的标准形式。

2. 学会绘制一次函数的图像，并能通过图像分析一次函数的性质。

3. 能够运用一次函数的图像解决实际问题，提高解决问题的能力。

三、教学难点与重点教学难点：一次函数图像的绘制及性质分析。

教学重点：一次函数的定义，图像特点及实际应用。

四、教具与学具准备教具：多媒体课件、黑板、粉笔。

学具：直尺、圆规、铅笔、橡皮、练习本。

五、教学过程1. 实践情景引入展示一次函数在实际生活中的应用实例，如气温变化、物体运动等，引导学生思考一次函数的特点。

2. 知识讲解（1）回顾函数的定义，引导学生理解一次函数的概念。

（2）讲解一次函数的标准形式：y=kx+b（k≠0），解释k、b的几何意义。

3. 例题讲解（1）绘制一次函数y=2x+1的图像。

（2）分析一次函数y=3x+4的图像特点。

4. 随堂练习让学生绘制几个一次函数的图像，并分析其性质。

5. 小结六、板书设计1. 一次函数定义2. 一次函数标准形式：y=kx+b（k≠0）3. 图像特点4. 绘制方法七、作业设计1. 作业题目：（1）绘制一次函数y=3x2的图像。

（2）分析一次函数y=4x+3的图像特点。

2. 答案：（1）图像为一条斜率为3，截距为2的直线。

（2）图像为一条斜率为4，截距为3的直线。

八、课后反思及拓展延伸1. 反思：本节课学生对一次函数的定义和图像特点掌握情况，以及图像绘制方法的熟练程度。

2. 拓展延伸：（1）探讨一次函数在坐标系中的位置关系。

（2）研究一次函数与一元一次方程、一元一次不等式的关系。

重点和难点解析1. 一次函数的定义及其标准形式。

2. 一次函数图像的绘制方法和特点。