4.2.2 指数函数应用举例

4.2.2指数函数的图象和性质(人教A版普通高中教科书数学必修第一册第四章)一、教学目标1.类比研究幂函数性质的过程和方法，通过指数函数图象得出其性质；2.利用指数函数的图象研究指数函数的性质，并用所得性质进一步理解指数函数的图象；3.通过信息技术手段更好地理解指数函数的图象和性质。

二、教学重难点1.教学重点：指数函数的图象和性质2.教学难点：指数函数性质的理解三、教学过程师生活动：从简单的函数2x y =入手，教师引导学生分析函数的性质，包括定义域，值域，奇偶性，单调性．由概念知定义域为R ，根据指数运算，分析值域为(0,)+∞，进而分析出函数的图象应该都在x 轴上方．通过特殊点的分析，得出函数不具有奇偶性．单调性需要借助图象研究．学生在列表时，分析x 的取值，要兼顾正值和负值，在性质指导下画出函数的图象．问题4：请同学们画出指数函数1()2x y =的图象，观察函数的图象.师生活动：教师布置任务，学生自己选择方法作图，观察图象，探究函数的性质．问题5：你是如何画出函数1()2x y =的图象？描点法还是利用对称性？请讲出选择的理由．师生活动：教师询问学生作图的方法，学生反馈自己用的是描点法还是利用了函数之间的对称性．因为1()22x x y -==，点(x ，y )与点(-x ，y )关于y 轴对称，所以函数2x y =图象上任意一点(,)P x y 关于y 轴的对称点1(,)P x y -都在函数1()2x y =的图象上，反之亦然．根据这种对称性，可以利用函数2x y =的图象，画出1()2xy =的图象．并将此结论推广：底数互为倒数的两个指数函数的图象关于y 轴对称，所以利用这种对称性，可以由一个函数的图象得到另一个函数的图象．设计意图：根据函数的解析式先初步分析函数的性质，再选择合适的点，利用描点法画出函数的图象，然后由图象概括出函数的性质，这是我们研究具体函数的过程．让学生观察两个具体的指数函数的图象，对指数函数的图象和性质有一个初步的认知．学生在作图的过程中得出结论：底数互为倒数的两个指数函数的图象关于y 轴对称．根据这种对称性，我们将指数函数x y a =的图象按底数a 的取值，分作1a >和01a <<两种类型进行研究．让学生学会用联系的观点看待问题．问题6：我们将指数函数x y a =的图象按底数a 的取值，分作1a >和01a <<两种类型进行研究．为了得到指数函数x y a =的性质，我们还需要画出更多的具体的指数函数的图象进行观察．问题7：画出指数函数3x y =和4x y =的图象，分析它们的性质．画出指数函数1()3x y =和1()4xy =的图象，分析它们的性质．师生活动：学生动手操作，观察分析，师生共同评价．教师指导学生先研究底数1a >的情况，可追问学生在1a >的范围内是否还需要进一步分类，为什么？引导学生还是要从具体的指数函数进行研究．学生画出指数函数3x y =和4x y =的图象，教师借助几何画板呈现多个函数的图象．观察图象，师生共同总结出图象的直观性质；当1a >时，底数越大越靠近y 轴，而当01a <<，底数越小越靠近y 轴，故底数互为倒数的两个指数函数图象关于y 轴对称。

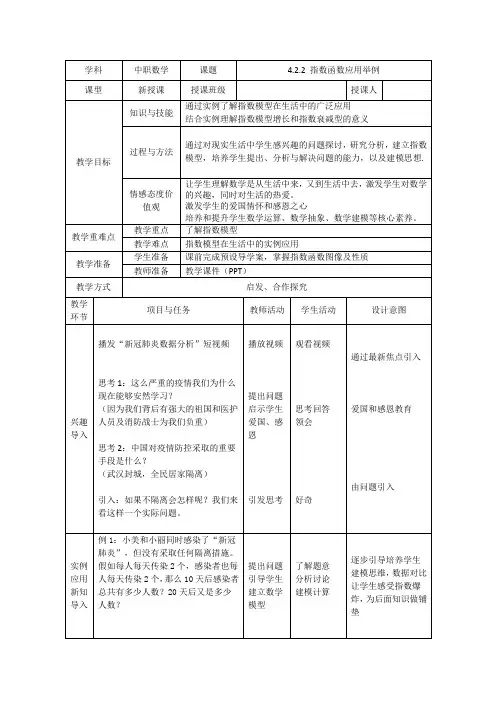
指数函数应用举例明确目标指数函数在自然科学和经济生活中有着广泛的应用，要了解指数函数的实际应用举例，能够应用指数函数的性质解决简单的实际问题。

合作交流例1 某市2008年国内生产总值为20亿元，计划在未来10年内，平均每年按8％的增长率增长，分别预测该市2013年与2018年的国内生产总值（精确到0.01亿元）例2 设磷-32经过一天的衰变，其残留量为原来的95.27％.现有10g磷-32，设每天的衰变速度不变，经过14天衰变还剩下多少克（精确到0.01g）？探究展示由上面两例题中的函数解析式都可以写成y=ca x的形式，其中c>0为常数，底a>0且a1≠.函数模型y=ca x叫做指数模型.当a>1时,叫做指数增长模型;当0<a<1时, 叫做指数衰减模型.例3 服用某种感冒药,每次服用的药物含量为,随着时间的变化，体内的药物含量为其中以小时为单位。

问服药4小时后，体内药物的含量为多少？8小时后，体内药物的含量为多少？拓展训练1我国工农业总平均值计划从2000年到2020年翻两番，设平均增长率为ｘ则（）A ()191x+=4 B ()201x+=3 C ()201x+=2 D ()201x+=42一种产品的年产量原来是ａ，计划使年产量平均每年比上一年增加ｐ，则年产量ｙ随着年数ｘ变化的关系为3某市2004年有常住人口54万，如果人口按每年1.2％的增长率增长，那么2010年该市常住人口约为多少万人（精确到0.01万）？4某放射性物质，每经过一年残留量是原来的89.64％，每年的衰变速度不变，问100g这样的物质，经过8年衰变还剩下多少克（精确到0.01g）？5某种细菌在培养过程中，每一小时分裂一次(一个分裂成两个)，经过5小时后，这种细菌可由一个繁殖成多少个?。

指数函数模型的生活中的例子指数函数模型是数学中的一种常见模型，可以用来描述某些现象或者过程的增长或衰减规律。

在我们的生活中，有许多例子都可以通过指数函数模型来解释和描述。

本文将介绍几个生活中常见的例子，并通过这些例子来理解指数函数模型的应用。

1. 人口增长模型人口增长是一个长期以来备受关注的问题。

指数函数模型可以用来描述人口增长的规律。

在指数函数模型中，人口数量随着时间的增加而指数级增长。

例如，某城市人口在初始时期为100万，年增长率为3%。

使用指数函数模型，我们可以得出人口数随时间增长的表达式为P(t) = 100万 * (1 + 0.03)^t，其中t为时间（年）。

利用这个模型，我们可以预测城市未来的人口数量，并制定合理的发展规划。

2. 财务投资模型财务投资是许多人关注的领域之一。

指数函数模型可以用来描述投资的增长规律。

例如，某投资项目的初始投资金额为1000万元，年化收益率为5%。

通过指数函数模型，我们可以计算出投资金额随时间的增长情况。

投资金额的表达式为A(t) = 1000万 * (1 + 0.05)^t，其中t为时间（年）。

利用这个模型，我们可以评估投资的回报率，并决定是否进行相应的投资。

3. 病毒传播模型疫情爆发时，病毒传播模型成为重要的研究方向。

指数函数模型可以用来描述病毒的传播速度和规模。

例如，某病毒的传染系数为1.1，即每个感染者平均会感染1.1个人。

通过指数函数模型，我们可以预测疫情的发展趋势。

疫情的增长可以用指数函数P(t) = P(0) * (1 + 1.1)^t 来描述，其中P(t)为时间t时刻的感染人数。

利用这个模型，可以对疫情的传播速度和规模进行评估，并采取相应的防控措施。

4. 化学反应速率模型化学反应速率也可以用指数函数模型来描述。

在某些反应中，反应物的浓度随着时间的推移呈指数级减少。

例如，一个化学反应的初始浓度为C0，反应速率常数为k。

反应物的浓度随时间的变化可以用指数函数模型C(t) = C0 * e^(-kt)来描述。

初中数学中如何运用指数函数解决实际问题在初中数学的学习中，指数函数是一个重要的数学概念，它不仅在理论上具有深刻的意义，更在解决实际问题中发挥着关键作用。

通过对指数函数的理解和运用，我们能够更好地描述和解决许多与现实生活密切相关的问题。

首先，让我们来明确一下什么是指数函数。

一般地，函数$y ＝a^x$（＄a ＞ 0$，且$a ≠ 1$）叫做指数函数，其中$x$是自变量。

指数函数的特点是底数$a$为常数，指数$x$为变量。

当$a ＞ 1$时，函数单调递增；当$0 ＜ a ＜ 1$时，函数单调递减。

那么，在实际生活中，指数函数究竟能帮助我们解决哪些问题呢？一个常见的应用是人口增长问题。

假设某个地区的初始人口为$P_0$，年增长率为$r$，经过$t$年后的人口数量$P(t)＄可以用指数函数$P(t) ＝ P_0(1 ＋ r)＾t$来表示。

例如，某城市的初始人口为 10 万人，年增长率为 2%，那么 5 年后的人口数量就可以通过计算$P(5) ＝ 10×（1 ＋ 002)＾5$得出。

再比如，细菌繁殖问题也可以用指数函数来描述。

假设某种细菌每小时繁殖的倍数为$k$，初始数量为$N_0$，经过$t$小时后的细菌数量$N(t) ＝ N_0×k^t$。

如果知道了初始细菌数量和繁殖倍数，就能够预测在一定时间后细菌的数量，这对于疾病防控和卫生管理具有重要意义。

在金融领域，指数函数也有广泛的应用。

例如，复利计算就是一个典型的例子。

如果一笔本金$P$以年利率$r$进行复利计算，投资$t$年后的本利和$A$可以表示为$A ＝ P(1 ＋ r)＾t$。

通过这个公式，我们可以计算出在不同的利率和投资时间下，资金的增长情况，从而帮助我们做出合理的投资决策。

另外，放射性物质的衰变也遵循指数函数的规律。

假设某种放射性物质的初始质量为$m_0$，半衰期为$T$，经过时间$t$后剩余的质量$m(t) ＝ m_0×（＼frac{1}｛2}）＾｛＼frac{t}｛T}｝＄。

指数函数在实际生活中的应用有哪些？
指数函数是一种常见的数学函数，其在实际生活中有许多应用。

以下是一些指数函数在实际生活中的应用示例：
1. 财务规划：指数函数可用于计算复利。

在投资中，复利是通
过将利息再投资于本金来实现的。

指数函数可以帮助确定投资增长
速度和最终价值。

这对个人的财务规划非常有用。

2. 科学研究：指数函数在科学研究中经常用于描述指数衰减和
指数增长的现象。

例如，在物理学中，指数函数可以描述放射性元
素的衰变速度。

在生物学领域，它可以描述细菌或病毒的增长速度。

3. 人口增长：指数函数可以用于描述人口增长的模型。

许多国
家和地区使用指数函数来预测人口的增长趋势和规模。

这对规划城
市和制定政策非常重要。

4. 市场营销：指数函数在市场营销中也发挥着重要的作用。

例如，市场份额的增长通常符合指数函数的规律。

通过分析指数函数，市场营销人员可以了解产品或服务的市场表现，并制定相应的策略。

5. 电子技术：指数函数在电子技术中有广泛的应用。

例如，在
电路设计中，指数函数可以用来描述电流或电压的变化。

它也用于
描述集成电路中的传输特性和放大效果。

这只是指数函数在实际生活中应用的一小部分示例。

指数函数
在各个领域都有广泛的用途，对于解决问题和做出决策非常有帮助。

指数函数的增长和衰减模型指数函数是一种常见的数学函数，它在很多领域中被广泛应用，如生物学、经济学、物理学等。

在这篇文章中，我们将讨论指数函数的增长和衰减模型，以及它们在实际问题中的应用。

1. 指数函数的定义指数函数是以常数e为底的幂函数，通常表示为f(x) = a * e^(kx)，其中a和k为常数，e是一个数学常数，约等于2.71828。

指数函数有两种基本类型：增长和衰减。

2. 指数函数的增长模型指数函数在x逐渐增大的情况下以指数速度增长。

即使初始值很小，随着x的增大，函数值也会迅速增加。

这种增长模型在多个领域中得到广泛应用，如人口增长、细菌繁殖等。

3. 指数函数的衰减模型相反，指数函数在x逐渐增大的情况下以指数速度衰减。

即使初始值很大，随着x的增大，函数值也会迅速减小。

这种衰减模型在自然衰变、物质衰变等问题中经常出现。

4. 指数函数的应用举例4.1 经济学中的应用指数函数常用于描述经济增长和指数增长模型。

例如，GDP的增长率可以用指数函数来描述，初始值通常表示为某个年份的GDP，随着时间的推移，GDP会以指数速度增长。

4.2 生物学中的应用许多生物过程也可以被指数函数所描述。

例如，细菌繁殖可以用指数函数来建模。

假设我们有一种细菌，每个小时繁殖的数量是当前细菌数量的两倍，那么用指数函数可以表示为f(x) = a * 2^x，其中x表示时间，a表示初始的细菌数量。

4.3 物理学中的应用指数函数在物理学中也有广泛的应用。

例如，在放射性衰变中，原子核的衰变速率可以用指数函数来描述。

指数函数的衰减模型可以帮助我们预测放射性物质的衰变过程。

5. 指数函数的性质指数函数具有一些特殊的性质。

例如，指数函数的图像总是经过点(0,1)，并且在x增大时，函数值增长快速。

同时，它的导数也是指数函数本身的常数倍，这使得指数函数在微积分中经常被使用。

6. 结论指数函数是一种重要的数学函数，它可以用来描述增长和衰减模型。

第四章 指数函数与对数函数（基础模块∙上）一、知识点节次知识点4.1实数指数幂4.1.1分数指数幂n 次方根 n 次算术根 n 次根式根指数 被开方数)0(10≠=a ann a a 1=- 4.1.2实数指数幂及其运算法则同底数幂相乘 幂的乘方 积的乘方 4.1.3幂函数举例幂函数定义 4.2指数函数4.2.1指数函数及其图像与性质 指数函数定义 指数函数性质 4.2.2指数函数应用举例指数模型增长模型、衰减模型 4.3对数4.3.1对数的概念对数、对数的底 真数对数的性质 4.3.2常用对数与自然对数 常用对数定义 自然对数定义 4.3.3积、商、幂的对数积、商、幂的对数 4.4对数函数4.4.1对数函数及其图像与性质 对数函数定义 对数函数性质 4.4.2对数函数应用举例阅读与欣赏 声音的计量及噪音二、结构展示分式指数幂指数函数与对数函数实数指数幂指数函数对数对数函数幂函数商的对数积的对数自然对数常用对数指数函数的应用指数函数的性质指数函数的图像指数函数的概念幂的对数对数的概念对数函数的概念对数函数的图像对数函数的性质对数函数的应用实数指数幂三、考纲解读1、有理数指数幂（理解）理解分数指数幂的含义，正确进行根式与分数指数幂之间的转化. 2、实数指数幂及其运算法则（掌握）掌握实数指数幂的含义，实数指数幂的运算法则. 3、幂函数举例（了解）了解幂函数的含义，了解常见幂函数的图像及性质.4、指数函数的图像和性质（理解）理解指数函数的概念、图像及性质；画出指数函数的简图；判断指数函数的单调性. 5、对数的概念（含常用对数、自然对数）（理解）理解对数的概念，正确进行指数式与对数式之间的互化；理解常用对数和自然对数的概念，对数的性质 .6、积、商、幂的对数（了解）了解积、商、幂的对数，会进行有关的计算． 7、对数函数的图像和性质（了解）了解对数函数的概念、图像及性质. 8、指数函数与对数函数的实际应用（了解）了解指数函数、对数函数的实际应用，会利用指数模型和对数函数模型解决一些实际问题.四、基本概念（一）实数指数幂1、一般地，如果a x n= (n ∈Ｎ*且n >1)，那么x 叫做a 的n 次方根．2、形如n a (n ∈Ｎ*且n >1)的式子叫做a 的n 次根式，其中n 叫做根指数，a 叫做被开方数．3、利用分数指数幂来表示根式，规定anm =n m a ，其中m 、n ∈Ｎ*且n >1)．当n 为奇数时，a ∈Ｒ；当n 为偶数时，a ≥0．当anm 有意义，且a ≠0，规定：nmnm aa1=-4、实数指数幂运算法则为：a p·a q＝qp a+；q p a )(＝apq；pab )( =pp ba （R q R pb a ∈∈>>,,,00）．5、一般地，形如αx y =（α∈Ｒ）的函数叫做幂函数．其中为常数，x 为自变量． （二）指数函数1、一般地，形如y ＝a x的函数叫做指数函数，其中底a （a ＞0且a ≠１）为常量．指数函数的定义域为Ｒ，值域为（0，+∞）．2、一般地，形如y ＝x ca ，（其中ｃ＞0为常数，底a ＞0且a ≠１）的函数模型叫做指数模型．当a ＞1时，叫做指数增长模型；当0＜a ＜1时，叫做指数衰减模型． 3、指数函数x a y =（a ＞0且a ≠１）的性质 ⑴ 函数的定义域为Ｒ，值域为（0，+∞）； ⑵ 当x = 0时，函数值y = 1；⑶ 当a ＞1时，函数在（﹣∞，+∞）内是增函数；当0＜a ＜1时，函数在（﹣∞，+∞）内是减函数．（三）对数1、如果a b＝Ｎ（a ＞0且a ≠１），那么b 叫做以为a 底Ｎ的对数，记作b ＝㏒a Ｎ．其中a 叫做对数的底，Ｎ叫做真数．2、以10为底的对数叫做常用对数，㏒10Ｎ简记为lg Ｎ．3、以e(e=2.71828…)为底的对数叫做自然对数，㏒e Ｎ简记为ln Ｎ．4、对数的性质⑴ ㏒a 1 = 0（a ＞0且a ≠１）； ⑵ ㏒a a = 1（a ＞0且a ≠１）；⑶ N ＞0，即零和负数没有对数． 5、积、商、幂的对数⑴ 积的对数 lg （ＭＮ）＝lg M ＋ lg N ( M > 0，Ｎ > 0 )； ⑵ 商的对数 lg （NM）＝lg M － lg N ( M > 0，Ｎ > 0 )； ⑶ 幂的对数 lg M n＝ｎlg M ( M > 0，Ｎ > 0 ) ．（四）对数函数1、一般地，形如x y a log =的函数叫做对数函数，其中a 为常数（a ＞0且a ≠１）．对数函数的定义域为（0，+∞），值域为Ｒ．2、对数函数ｙ＝㏒a ｘ（a ＞0且a ≠１）的性质 ⑴ 函数的定义域为（0，+∞），值域为Ｒ； ⑵ 当 x = 1时，函数值y = 0；⑶ 当a ＞1时，函数在（0，+∞）内是增函数；当0＜a ＜1时，函数在（0，+∞）内是减函数．五、对口高考真题1.在不考虑空气阻力的条件下，火箭的最大速度V (m/s)和燃料的质量M (kg)，火箭（除燃料外）的质量m (kg)的函数关系是V =2000I n (l+Mm)。