人教版高一物理必修1暑假巩固专题3 力的合成与分解

教学设计：新2024秋季高中物理必修第一册人教版第三章相互作用——力《力的合成与分解》教学目标（核心素养）1.物理观念：理解力的合成与分解的概念，掌握平行四边形定则及其在力的合成与分解中的应用。

2.科学思维：通过实例分析和实验探究，培养学生将复杂问题简化为基本物理模型的能力，以及运用数学工具解决物理问题的能力。

3.科学探究：引导学生通过实验探究力的合成与分解的规律，培养观察、测量、记录和分析实验数据的能力。

4.科学态度与责任：激发学生对物理现象的好奇心和探索欲，培养严谨的科学态度和实事求是的精神，同时认识到力学知识在日常生活和工程技术中的应用价值。

教学重点•力的合成与分解的概念及平行四边形定则。

•运用平行四边形定则进行力的合成与分解的计算。

教学难点•理解平行四边形定则的几何意义和物理意义。

•灵活运用平行四边形定则解决复杂情境下的力的合成与分解问题。

教学资源•多媒体课件：包含力的合成与分解的动画演示、实例分析、平行四边形定则的几何解释等。

•实验器材：细绳、弹簧秤、木板、橡皮筋、刻度尺等，用于演示和探究力的合成与分解。

•黑板或白板及书写工具：用于板书关键概念和解题步骤。

•学生作业本：用于记录课堂笔记和练习。

教学方法•讲授法：通过教师讲解，引导学生理解力的合成与分解的基本概念和平行四边形定则。

•演示法：利用多媒体或实验器材演示力的合成与分解的过程，帮助学生直观理解。

•实验探究法：组织学生进行实验探究，亲身体验力的合成与分解的规律。

•讨论法：针对复杂情境下的力的合成与分解问题，组织学生讨论解决方案，促进思维碰撞。

教学过程导入新课•生活实例引入：展示工人利用滑轮组提升重物的图片或视频，提问学生：为什么两个较小的力可以合力提起一个较重的物体？引出力的合成概念。

•复习旧知：简要回顾矢量与标量的区别，为力的合成与分解是矢量运算做铺垫。

新课教学1.力的合成概念讲解：•定义：两个或多个力共同作用在一个物体上，产生的效果与一个力单独作用时相同，则这几个力可以合成为一个力，这个力称为这几个力的合力。

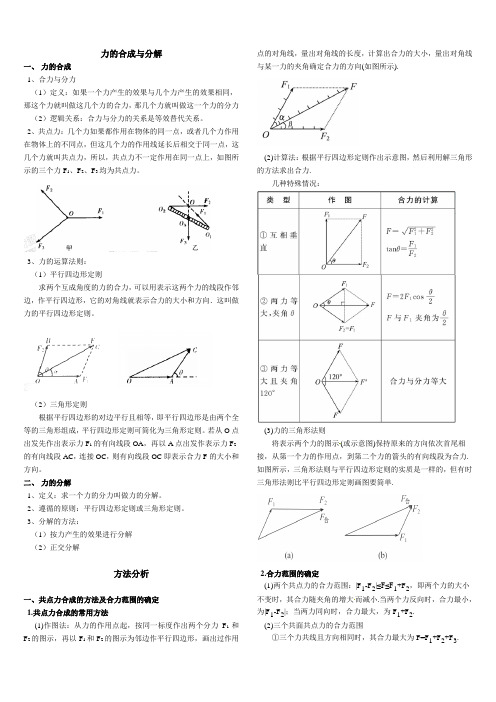
力的合成与分解一、力的合成1、合力与分力（1）定义：如果一个力产生的效果与几个力产生的效果相同，那这个力就叫做这几个力的合力，那几个力就叫做这一个力的分力（2）逻辑关系：合力与分力的关系是等效替代关系。

2、共点力：几个力如果都作用在物体的同一点，或者几个力作用在物体上的不同点，但这几个力的作用线延长后相交于同一点，这几个力就叫共点力，所以，共点力不一定作用在同一点上，如图所示的三个力F1、F2、F3均为共点力。

3、力的运算法则：（1）平行四边形定则求两个互成角度的力的合力，可以用表示这两个力的线段作邻边，作平行四边形，它的对角线就表示合力的大小和方向．这叫做力的平行四边形定则。

（2）三角形定则根据平行四边形的对边平行且相等，即平行四边形是由两个全等的三角形组成，平行四边形定则可简化为三角形定则。

若从O点出发先作出表示力F1的有向线段OA，再以A点出发作表示力F2的有向线段AC，连接OC，则有向线段OC即表示合力F的大小和方向。

二、力的分解1、定义：求一个力的分力叫做力的分解。

2、遵循的原则：平行四边形定则或三角形定则。

3、分解的方法：（1）按力产生的效果进行分解（2）正交分解方法分析一、共点力合成的方法及合力范围的确定1.共点力合成的常用方法(1)作图法：从力的作用点起，按同一标度作出两个分力F1和F2的图示，再以F1和F2的图示为邻边作平行四边形，画出过作用点的对角线，量出对角线的长度，计算出合力的大小，量出对角线与某一力的夹角确定合力的方向(如图所示).(2)计算法：根据平行四边形定则作出示意图，然后利用解三角形的方法求出合力.几种特殊情况：(3)力的三角形法则将表示两个力的图示(或示意图)保持原来的方向依次首尾相接，从第一个力的作用点，到第二个力的箭头的有向线段为合力. 如图所示，三角形法则与平行四边形定则的实质是一样的，但有时三角形法则比平行四边形定则画图要简单.2.合力范围的确定(1)两个共点力的合力范围：|F1-F2|≤F≤F1+F2，即两个力的大小不变时，其合力随夹角的增大而减小.当两个力反向时，合力最小，为|F1-F2|；当两力同向时，合力最大，为F1+F2.(2)三个共面共点力的合力范围①三个力共线且方向相同时，其合力最大为F=F1+F2+F3.②以这三个力的大小为边，如果能组成封闭的三角形，则其合力最小值为零，若不能组成封闭的三角形，则合力最小值的大小等于最大的一个力减去另外两个力的和的绝对值.注意： 进行力的合成时，要注意正确理解合力与分力的关系.(1)效果关系：合力的作用效果与各分力共同的作用效果相同，它们具有等效替代性.(2)大小关系：合力与分力谁大谁小要视具体情况而定，不能形成合力总大于分力的固定思维.【例1】一物体受到三个共面共点力F 1、F 2、F 3的作用，三力的矢量关系如图所示(小方格边长相等)，则下列说法正确的是()A ．三力的合力有最大值F 1＋F 2＋F 3，方向不确定B ．三力的合力有唯一值3F 3，方向与F 3同向[来源:学|科|网]C ．三力的合力有唯一值2F 3，方向与F 3同向D ．由题给条件无法求出合力大小 【答案】B【详解】由图可知，F 1和F 2在竖直方向的分力等大反向，其合力为零；在水平方向的合力分别为32F 3和12F 3，因而三力的合力有唯一值3F 3，方向与F 3同向，B 正确． 二、分解力的方法1.按力产生的效果进行分解2.正交分解将已知力按互相垂直的两个方向进行分解的方法. (1)一般选共点力的作用点为原点，建立坐标轴的原则如下： ①静力学中：以少分解力和容易分解力为原则(即尽量多的力在坐标轴上).②动力学中：以加速度方向和垂直加速度方向为坐标轴建立坐标系，这样使牛顿第二定律表达式变为F x =0；F y =ma y .(2)方法：物体受到多个力作用F 1、F 2、F 3……,求合力F 时,可把各力沿相互垂直的x 轴、y 轴分解.x 轴上的合力 F x =F x1+F x2+F x3+… y 轴上的合力F y = F y1+F y2+F y3+… 合力大小：合力方向：与x 轴夹角为θ，则注意：(1)在实际问题中进行力的分解时，有实际意义的分解方法是按力的实际效果进行分解，其他的分解方法都是为了解题方便而利用的.(2)力的正交分解是在物体受三个或三个以上的共点力作用下求合力的一种方法，分解的目的是为了更方便地求合力，将矢量运算转化为代数运算.【例2】某压榨机的结构示意图如图所示，其中B 点为固定铰链，若在A 铰链处作用一垂直于壁的力F ，则由于力F 的作用，使滑块C 压紧物体D ，设C 与D 光滑接触，杆的重力不计，压榨机的尺寸如图所示，求物体D 所受压力大小是F 的多少倍?【答案】5倍【详解】力F 的作用效果是对AB 、AC 两杆产生沿两杆方向的压力F 1、F 2，如图甲，力F 1的作用效果是对C 产生水平向左的推力和竖直向下的压力,将力F 1沿水平方向和竖直方向分解，如图乙，可得到C 对D 的压力F N ′=F N . (3分)由题图可看出 (3分)依图甲有：依图乙有：F′N =F 1sinα (3分) 故可以得到：所以物体D 所受的压力是F 的5倍 (3分)练 习1.如图5所示的水平面上，橡皮绳一端固定，另一端连接两根弹簧，连接点P 在F 1、F 2和F 3三力作用下保持静止。

4力的合成和分解[学习目标] 1.通过实际生活实例,体会等效替代物理思想．(重点) 2.通过实验探究,得出求合力的方法——平行四边形定则．(重点) 3.会用作图法和直角三角形的知识求共点力的合力与分解．(难点) 4.运用力的合成与分解知识分析日常生活中的相关问题,培养将物理知识应用于生活和生产实践的意识．一、合力和分力假设一个力单独作用的效果跟某几个力共同作用的效果相同,这个力就叫作那几个力的合力．这几个力就叫作那个力的分力．二、力的合成和分解1．定义：求几个力的合力的过程叫作力的合成；求一个力的分力的过程叫作力的分解．2．平行四边形定则：在两个力合成时,以表示这两个力的有向线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向．3．分解法则：遵循平行四边形定则．把一个已知力F作为平行四边形的对角线,与力F共点的平行四边形的两个邻边,就表示力F的两个分力F1和F2.4．分解依据(1)一个力分解为两个力,如果没有限制,可以分解为无数对大小、方向不同的分力．(2)实际问题中,要依据力的实际作用效果或需要分解．三、矢量和标量1．矢量：既有大小,又有方向,相加时遵从平行四边形定则或三角形定则的物理量．2．标量：只有大小,没有方向,相加时遵从算术法则的物理量．3．三角形定则：把两个矢量首尾相接,从第一个矢量的始端指向第二个矢量的末端的有向线段就表示合矢量的大小和方向．三角形定则与平行四边形定则实质上是一样的．1．正误判断(正确的打“√”,错误的打“×”)(1)合力与分力同时作用在一个物体上．(×)(2)由力的平行四边形定则可知,合力可能小于分力．(√)(3)把已知力F分解为两个分力F1与F2,此时物体受到F、F1、F2三个力的作用．(×)(4)既有大小,又有方向的物理量一定是矢量．(×)(5)矢量与标量的本质区别是它们的运算方法不同．(√)2．(多选)将力F分解为F1、F2两个分力,则下列说法正确的是( )A．F1、F2和F同时作用在物体上B．由F求F1或F2叫作力的分解C．由F1、F2求F叫作力的合成D．力的合成与分解都遵循平行四边形定则BCD[分力和合力是等效替代关系,不能同时作用在物体上,A错；由力的合成和分解的概念可知B、C 正确．力的合成和分解都是矢量运算,都遵循平行四边形定则,D正确．]3．(多选)关于几个力与其合力,下列说法正确的是( )A．合力的作用效果跟原来那几个力共同作用产生的效果相同B．合力与原来那几个力同时作用在物体上C．合力的作用可以替代原来那几个力的作用D．求几个共点力的合力遵循力的平行四边形定则ACD[合力与分力是“等效替代”的关系,即合力的作用效果与几个分力共同作用时的效果相同,合力的作用效果可以替代这几个分力的作用效果,不能认为合力与分力同时作用在物体上,所以A、C正确,B错误；求合力应遵循力的平行四边形定则,所以D正确．]力的合成1.合力的计算方法(1)作图法根据平行四边形定则用作图工具作出平行四边形,后用测量工具测量出合力的大小、方向,具体操作流程如下：(2)计算法两分力共线时：①若F1与F2方向相同,则合力大小F＝F1＋F2,方向与F1和F2的方向相同；②若F1与F2方向相反,则合力大小F＝|F1－F2|,方向与F1和F2中较大的方向相同．两分力不共线时：可以先根据平行四边形定则作出分力及合力的示意图,然后由几何知识求解对角线,即为合力．以下为求合力的两种常见特殊情况：类型作图合力的计算两分力相互垂直大小：F＝F21＋F22方向：tan θ＝F1F2两分力等大,夹角为θ大小：F＝2F1cosθ2方向：F与F1夹角为θ2(1)合力与分力间的大小关系当两分力F1、F2大小一定时：①最大值：两力同向时合力最大,F＝F1＋F2,方向与两力同向．②最小值：两力方向相反时,合力最小,F＝|F1－F2|,方向与两力中较大的力同向．③合力范围：两分力的夹角θ(0°≤θ≤180°)不确定时,合力大小随夹角θ的增大而减小,所以合力大小的范围是：|F1－F2|≤F≤F1＋F2.(2)三个力合力范围的确定①最大值：当三个力方向相同时,合力F最大,F max＝F1＋F2＋F3.②最小值：若其中两个较小的分力之和(F1＋F2)≥F3时,合力的最小值为零,即F min＝0；若其中两个较小的分力之和(F1＋F2)<F3时,合力的最小值F min＝F3－(F1＋F2)．③合力的取值范围：F min≤F≤F1＋F2＋F3.【例1】如图所示,水平横梁一端A插在墙壁内,另一端装有一小滑轮B.一轻绳的一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量为m＝10 kg的重物,∠CBA＝30°,则滑轮受到绳子的作用力大小为(g取10 N/kg)( )A．50 N B．60 NC．120 N D．100 N思路点拨：①轻绳跨过定滑轮,BC段绳和BD段绳的拉力大小相等．②重物静止,BD段绳的拉力为mg＝100 N.③BC段和BD段绳的拉力间夹角为120°.D[轻绳跨过滑轮,BC段、BD段拉力F1＝F2＝mg＝100 N,夹角为120°,根据平行四边形定则,二力合成如图所示．由于F1＝F2,所以平行四边形为菱形,又因为∠DBE＝60°,所以△BDE为等边三角形,所以F1、F2的合力F＝F1＝F2＝100 N,即绳子对滑轮的作用力大小为100 N,选项D正确．]上例中,若将横梁一端A处改为铰链,绳子系于横梁另一端B处,此时横梁恰好水平,如图所示．则AB 杆和BC绳所受弹力分别为多大？[提示] AB杆和BC绳合力与BD绳的拉力大小相等,方向相反,即F BC＝F BDsin 30°＝200 NF AB＝F BD tan 60°＝100 3 N.解决分力与合力问题的注意点(1)作图法求合力①作图时要先确定力的标度,同一图上的各个力必须采用同一标度．②严格采用作图工具作图,并用测量工具测出对应力的大小及方向．③作图时表示分力和合力的有向线段共点且要画成实线,与分力平行的对边要画成虚线,表示力的线段上要画上刻度和箭头．(2)计算法求合力时常用到的几何知识①应用直角三角形中的边角关系求解,适用于平行四边形的两边垂直、平行四边形的对角线与一条边垂直及菱形的情况．②应用等边三角形的特点求解．③应用相似三角形的知识求解,适用于力的矢量三角形与实际三角形相似的情况．1. 如图所示,两个人共同用力将一个牌匾拉上墙头．其中一人用了450 N的拉力,另一人用了600 N 的拉力,如果这两个人所用拉力的夹角是90°,求合力．[解析]解法一：作图法用图示中的线段表示150 N的力．用一个点O代表牌匾,依题意作出力的平行四边形,如图所示．用刻度尺量出平行四边形的对角线长为图示线段的5倍,故合力大小为F＝150×5 N ＝750 N,用量角器量出合力F与F1的夹角θ＝53°.解法二：计算法设F 1＝450 N,F 2＝600 N,合力为F.由于F 1与F 2间的夹角为90°,根据勾股定理得 F ＝4502＋6002N ＝750 N 合力F 与F 1的夹角θ的正切值 tan θ＝F 2F 1＝600 N 450 N ＝43所以θ＝53°.[答案] 750 N,与较小拉力的夹角为53°力的分解1.,从理论上讲有无数组解,因为同一条对角线可以构成的平行四边形有无穷多个(如图所示),这样分解是没有实际意义的．实际分解时,一个力按力的作用效果可分解为一组确定的分力．2．一个合力分解为一组分力的情况分析 (1)已知合力和两个分力的方向时,有唯一解．甲 乙(2)已知合力和一个分力的大小和方向时,有唯一解．甲 乙(3)已知合力F 以及一个分力F 1的方向和另一个分力F 2的大小时,若F 与F 1的夹角为α,有下面几种可能：①当Fsin α＜F 2＜F 时,有两解,如图甲所示； ②当F 2＝Fsin α时,有唯一解,如图乙所示； ③当F 2＜Fsin α时,无解,如图丙所示； ④当F 2＞F 时,有唯一解,如图丁所示．【例2】 把一个80 N 的力F 分解成两个分力F 1、F 2,其中力F 1与F 的夹角为30°,求： (1)当F 2最小时,另一个分力F 1的大小； (2)F 2＝50 N 时,F 1的大小．[解析] (1)当F 2最小时,如图甲所示,F 1和F 2垂直,此时F 1＝Fcos 30°＝80×32N ＝40 3 N.甲 乙(2)根据图乙所示,Fsin 30°＝80 N×12＝40 N ＜F 2则F 1有两个值． F 1′＝Fcos 30°－F 22－F·sin 30°2＝(403－30) NF 1″＝(403＋30) N.[答案] (1)40 3 N (2)(403－30) N 或(403＋30) N1画矢量图是解决力的分解问题的有效途径.2涉及“最大”“最小”等极值问题时,可多画几种不同情形的图,通过比较鉴别正确情景.2．把一个已知力分解,要求其中一个分力F 1跟F 成30°,而大小未知；另一个分力F 2＝33F,但方向未知,则F 1的大小可能是( )A.12F B.32F C.233F D.3FC [如图所示,由于F 2<F 2＝33F<F,所以F 1的大小有两种情况,根据F 2＝33F 可知,F 2有两个方向,F 21和F 22,对应F 21利用几何关系可以求得F 11＝33F,对应F 22利用几何关系得F 12＝233F,选项C 正确．]根据力的作用效果分解力1.对一个实际力的分解问题,关键是根据力的作用效果确定力的分解方向,然后再画出力的平行四边形,这样问题就转化为了一个根据已知边角关系进行求解的几何问题．其基本思路可表示为：2．常见典型力的分解实例 实例分析地面上物体受到斜向上的拉力F,拉力F 一方面使物体沿水平地面前进,另一方面向上提物体,因此拉力F 可分解为水平向前的力F 1和竖直向上的力F 2,F 1＝F cos θ,F 2＝F sin θ(θ为拉力F 与水平方向的夹角)放在斜面上的物体的重力产生两个效果：一是使物体具有沿斜面下滑的趋势；二是使物体压紧斜面；相当于分力F 1、F 2的作用,F 1＝mg sin α,F 2＝mg cos α(α为斜面倾角)用斧头劈柴时,力F 产生的作用效果为垂直于两个侧面向外挤压接触面,相当于分力F 1、F 2的作用,且F 1＝F 2＝Ld F质量为m 的光滑小球被竖直挡板挡住而静止于斜面上时,其重力产生两个效果：一是使球压紧挡板,相当于分力F 1的作用；二是使球压紧斜面,相当于分力F 2的作用,F 1＝mg tan α,F 2＝mg cos α(α为斜面倾角)A 、B 两点位于同一平面内,质量为m 的物体被AO 、BO 两绳拉住,其重力产生两个效果：一是使物体拉AO 绳,相当于分力F 1的作用；二是使物体拉BO 绳,相当于分力F 2的作用,F 1＝F 2＝mg2 sin α质量为m 的光滑小球被悬线挂靠在竖直墙壁上,其重力产生两个效果：一是使球垂直压紧墙面,相当于分力F 1的作用；二是使球拉线,相当于分力F 2的作用,F 1＝mg tan α,F 2＝mgcos α质量为m 的物体被OA 、OB 两线拉住,OB 水平,连接物体的绳的拉力产生两个效果：一是拉紧OA 线,相当于分力F 1的作用；二是拉紧OB 线,相当于分力F 2的作用,F 1＝mgcos θ,F 2＝mg tan θ质量为m的物体被支架悬挂而静止(OA为杆,OB可绳可杆),连接物体的绳的拉力产生两个效果：一是压杆OA,相当于分力F1的作用；二是拉OB,相当于分力F2的作用,F1＝mgtan θ,F2＝mgsin θ质量为m的物体被支架悬挂而静止,连接物体的绳的拉力产生两个效果：一是拉AB,相当于分力F1的作用,二是压BC,相当于分力F2的作用,F1＝mg tan α,F2＝mgcos α常见典型力的分解实例可分成面模型、绳模型、杆模型．1．面模型中,力的作用效果往往垂直于面．2．绳模型中,力的作用效果往往沿着绳．3．杆模型中,力的作用效果不一定沿着杆：如果杆与墙是转动连接(用可转动的滑轮相连),力的作用效果就沿着杆,其他情况,力的作用效果不一定沿着杆．【例3】如图所示,一个重为100 N的小球被夹在竖直的墙壁和A点之间,已知球心O与A点的连线与竖直方向成θ角,且θ＝60°,所有接触点和面均不计摩擦．试求小球对墙面的压力F1和对A点压力F2.[解析]小球的重力产生两个作用效果：压紧墙壁和A点,作出重力及它的两个分力F1′和F2′,构成的平行四边形,如图所示．小球对墙面的压力F1＝F1′＝mgtan 60°＝100 3 N,方向垂直墙壁向右；小球对A点的压力F2＝F2′＝mgcos 60°＝200 N,方向沿OA方向．[答案]见解析上例中,若将竖直墙壁改为与左端相同的墙角B撑住小球且B端与A端等高,则小球对墙角的压力分别为多大？方向如何？[提示]由几何关系知：F A＝F B＝mg＝100 N,故小球对A、B点的压力大小都为100 N,方向分别沿OA、OB方向．按作用效果分解力的一般思路3．将物体所受重力按力的效果进行分解,下列图中错误的是( )A B C DC[A项中物体重力分解为垂直于斜面使物体压紧斜面的分力G1和沿斜面向下使物体向下滑的分力G2；B项中物体的重力分解为沿两条细绳使细绳张紧的分力G1和G2,A、B项图均画得正确．C项中物体的重力应分解为垂直于两接触面使物体压紧两接触面的分力G1和G2,故C项图画错．D项中物体的重力分解为水平向左压紧墙的分力G1和沿绳向下使绳张紧的分力G2,故D项图画得正确．]课堂小结知识脉络1.合力与分力产生的效果相同,具有等效替代关系.2.求几个力的合力的过程叫作力的合成,求一个力的分力叫力的分解．力的分解是力的合成的逆运算,同样遵循平行四边形定则.3.两个力合成时,以表示这两个力的线段为邻边作平行四边形,这两个邻边之间的对角线就代表合力的大小和方向,这个法则叫作平行四边形定则.4.两个分力F1、F2与其合力F的关系：|F1－F2|≤F≤F1＋F2.5.矢量运算遵循平行四边形定则；标量运算遵循算术运算法则.1．(多选)关于F1、F2及它们的合力F,下列说法正确的是( )A．合力F一定与F1、F2共同作用产生的效果相同B．两力F1、F2一定是同种性质的力C．两力F1、F2一定是同一物体受到的力D．两力F1、F2与F是物体同时受到的三个力AC[只有同一个物体受到的力才能合成,分别作用在不同物体上的力不能合成,C正确；合力是对原来几个分力的等效替代,各分力可以是不同性质的力,合力与分力不能同时存在,A正确,B、D错误．] 2．如图所示,挑水时水桶上绳子连接状态分别如图中a、b、c三种情况．下列说法中正确的是( )A．a状态绳子受力大容易断B．b状态绳子受力大容易断C．c状态绳子受力大容易断D．a、b、c三种状态绳子受力都一样A[桶的重力产生两个效果,即沿绳子的两个分力,由平行四边形定则可知,绳子的夹角越大,绳子的分力越大,a绳夹角最大,故A正确．]3．两个共点力F1和F2的合力大小为6 N,则F1与F2的大小可能是( )A．F1＝2 N,F2＝9 N B．F1＝4 N,F2＝8 NC．F1＝1 N,F2＝8 N D．F1＝2 N,F2＝1 NB[两力合成时,合力范围为：|F1－F2|≤F≤F1＋F2,A中合力为7 N≤F≤11 N,B中合力为4 N≤F≤12 N,C中的合力为7 N≤F≤9 N,D中的合力为1 N≤F≤3 N,故B正确．]4．如图所示,一条小船在河中向正东方向行驶,船上挂起一风帆,帆受侧向风作用,风力大小F1为100 N,方向为东偏南30°,为了使船受到的合力能恰沿正东方向,岸上一人用一根绳子拉船,绳子取向与河岸垂直,求出风力和绳子拉力的合力大小及绳子拉力F2的大小．[解析]如图所示,以F1、F2为邻边作平行四边形,使合力F沿正东方向,则F ＝F 1cos 30°＝100×32N ＝50 3 N F 2＝F 1sin 30°＝100×12N ＝50 N.[答案] 50 3 N 50 N。

力的合成和分解课后篇巩固提升合格考达标练1.(2021陕西宝鸡高一期末)在力的合成中,关于两个分力与它们合力的关系,下列说法中正确的是()A.合力大小一定等于两个分力大小之和B.合力的方向一定与分力的方向相同C.合力大小一定比任何一个分力都大D.两个分力不变且两个分力的夹角在0~180°之间变化时,夹角越大合力越小,合力大小不一定是等于两个分力大小之和,A错误;由力的平行四边形定则可知,合力的方向不一定与分力的方向相同,B错误;当两个力方向相同时,合力等于两分力之和,合力大于每一个分力;当两个分力方向相反时,合力等于两个分力之差,合力可能小于分力,由此可见:合力可能大于分力也有可能小于分力,C错误;当夹角在0~180°之间变化时,由公式F=√F12+F22+2F1F2cosθ,知夹角越大合力越小,D正确。

2.如图所示,轻绳OA、OB和OP将一只元宵花灯悬挂在P点,花灯保持静止。

已知绳OA和OB的夹角为120°,对O点拉力的大小皆为F,轻绳OP对O点拉力的大小为()A.FB.√2FC.√3FD.2FOP对O点拉力的大小等于绳OA和OB的拉力的合力,根据几何知识可知,应为F。

3.(2021山西长治高一月考)三个共点力F1、F2、F3可用如图所示的有向线段表示,它们围成封闭的三角形。

则这三个力的合力最大的是()中F1和F2的合力为-F3,合力等于0;B中F1和F3的合力为F2,合力等于2F2;C中F1和F2的合力为F3,合力等于2F3;D中F2和F3的合力为F1,合力等于2F1;由上可知2F1最大,故选D。

4.如图甲为射箭比赛时的场景。

已知弓的顶部跨度为l,且拉弓过程中l保持不变;弦均匀且弹性良好,其自由长度也为l,劲度系数为k;射箭时弦和箭可等效为图乙情景:箭在弦的正中间,弦夹在类似动滑轮的附加装置上,将箭发射出去。

发射箭时弦的最大长度为2l,设弦的弹力满足胡克定律,则箭被发射瞬间所受的弹力为()kl B.kl C.√3kl D.2klA.√32,两侧弦和虚线构成一个正三角形,则弦伸长的长度为x=2l-l=l,由胡克定律知,弦上的拉力为F=kx=kl,两侧弦之间的夹角为60°,则箭受到的弹力,即两侧弦的拉力的合力为F'=2F cos 30°=√3kl。

第14讲力的合成和分解1.通过实验探究，得出力的合成与分解遵从的规律——平行四边形定则。

2.会用作图法和直角三角形的知识解决共点力的合成与分解问题。

3.运用力的合成与分解知识分析日常生活中的相关问题，培养将物理知识应用于生活和生产实践的意识。

一、合力和分力1.共点力：几个力如果都作用在物体的同一点，或者它们的作用线相交于一点，这几个力叫作共点力。

2.合力与分力：假设一个力单独作用的效果跟某几个力共同作用的效果相同，这个力就叫作那几个力的合力。

假设几个力共同作用的效果跟某个力单独作用的效果相同，这几个力就叫作那个力的分力。

二、力的合成和分解1.力的合成(1)定义：求几个力的合力的过程。

(2)合成规律：两个力合成时，以表示这两个力的有向线段为邻边作平行四边形，这两个邻边之间的对角线表示合力的大小和方向，这个规律叫作平行四边形定则。

(3)多个力的合成：先求出任意两个力的合力，再求出这个合力跟第三个力的合力，直到将所有的力都合成进去。

2.力的分解(1)定义：求一个力的分力的过程。

(2)分解规律：力的分解是力的合成的逆运算，同样遵从平行四边形定则。

三、求合力的方法1.作图法：根据平行四边形定则用作图工具作出平行四边形，然后用测量工具测量出合力的大小、方向，具体操作流程如下：2.计算法：(1)两分力共线时①若F 1、F 2两力同向，则合力F ＝F 1＋F 2，方向与两力同向。

此时合力最大②若F 1、F 2两力反向，则合力F ＝|F 1－F 2|，方向与两力中较大的同向。

此时合力最小(2)两分力不共线时可以根据平行四边形定则作出分力及合力的示意图，然后由几何知识求解对角线，即为合力。

以下为求合力的三种特殊情况：类型作图合力的计算两分力相互垂直大小：F＝F 21＋F 22方向：tan θ＝F 1F 2两分力等大，夹角为θ大小：F ＝2F 1cosθ2方向：F 与F 1夹角为θ2(当θ＝120°时，F ＝F 2＝F 1)合力与其中一个分力垂直大小：F ＝F 22－F 21方向：sin θ＝F 1F 2四、力的分解方法1.按照例力的实际作用效果分解(1)分解原则：根据力的作用效果确定分力的方向，然后再画出力的平行四边形。