第三章判别函数分类器
- 格式:ppt
- 大小:478.50 KB
- 文档页数:36


《模式识别》试题库一、基本概念题1.1 模式识别的三大核心问题是:、、。
1.2、模式分布为团状时,选用聚类算法较好。
1.3 欧式距离具有。
马式距离具有。
(1)平移不变性(2)旋转不变性(3)尺度缩放不变性(4)不受量纲影响的特性1.4 描述模式相似的测度有:。
(1)距离测度(2)模糊测度(3)相似测度(4)匹配测度1.5 利用两类方法处理多类问题的技术途径有:(1);(2);(3)。
其中最常用的是第个技术途径。
1.6 判别函数的正负和数值大小在分类中的意义是:,。
1.7 感知器算法。
(1)只适用于线性可分的情况;(2)线性可分、不可分都适用。
1.8 积累位势函数法的判别界面一般为。
(1)线性界面;(2)非线性界面。
1.9 基于距离的类别可分性判据有:。
(1)1[]w BTr S S-(2)BWSS(3)BW BSS S+1.10 作为统计判别问题的模式分类,在()情况下,可使用聂曼-皮尔逊判决准则。
1.11 确定性模式非线形分类的势函数法中,位势函数K(x,x k)与积累位势函数K(x)的关系为()。
1.12 用作确定性模式非线形分类的势函数法,通常,两个n维向量x和x k的函数K(x,x k)若同时满足下列三个条件,都可作为势函数。
①();②( ); ③ K(x,x k )是光滑函数,且是x 和x k 之间距离的单调下降函数。
1.13 散度J ij 越大,说明ωi 类模式与ωj 类模式的分布( )。
当ωi 类模式与ωj 类模式的分布相同时,J ij =( )。
1.14 若用Parzen 窗法估计模式的类概率密度函数,窗口尺寸h1过小可能产生的问题是( ),h1过大可能产生的问题是( )。
1.15 信息熵可以作为一种可分性判据的原因是: 。
1.16作为统计判别问题的模式分类,在( )条件下,最小损失判决规则与最小错误判决规则是等价的。
1.17 随机变量l(x )=p( x |ω1)/p( x |ω2),l( x )又称似然比,则E {l( x )|ω2}=( )。


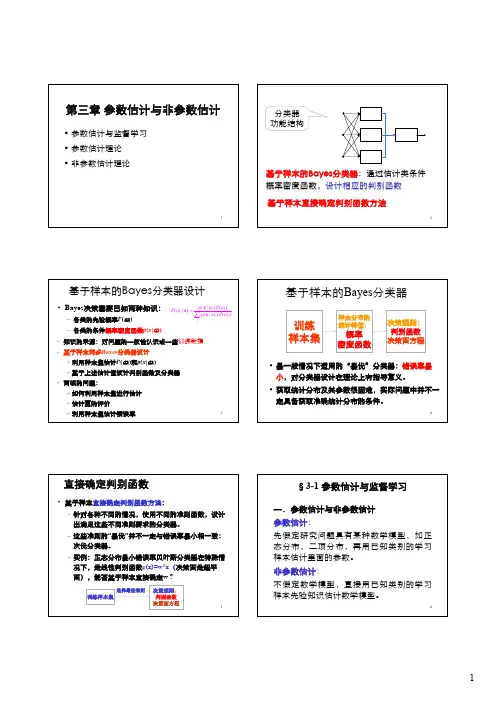
1第三章参数估计与非参数估计•参数估计与监督学习•参数估计理论•非参数估计理论2基于样本的Bayes分类器:通过估计类条件概率密度函数,设计相应的判别函数分类器功能结构基于样本直接确定判别函数方法3基于样本的Bayes 分类器设计•Bayes 决策需要已知两种知识:–各类的先验概率P (ωi )–各类的条件概率密度函数p(x |ωi )(|)()(|)(|)()i i i j j jp P P p P ωωωωω=∑x x x 知识的来源:对问题的一般性认识或一些训练数据基于样本两步Bayes 分类器设计¾利用样本集估计P (ωi )和p(x |ωi )¾基于上述估计值设计判别函数及分类器面临的问题:¾如何利用样本集进行估计¾估计量的评价¾利用样本集估计错误率4基于样本的Bayes 分类器训练样本集样本分布的统计特征:概率密度函数决策规则:判别函数决策面方程•最一般情况下适用的“最优”分类器:错误率最小,对分类器设计在理论上有指导意义。
•获取统计分布及其参数很困难,实际问题中并不一定具备获取准确统计分布的条件。
5直接确定判别函数•基于样本直接确定判别函数方法:–针对各种不同的情况,使用不同的准则函数,设计出满足这些不同准则要求的分类器。
–这些准则的“最优”并不一定与错误率最小相一致:次优分类器。
–实例:正态分布最小错误率贝叶斯分类器在特殊情况下,是线性判别函数g (x)=w T x (决策面是超平面),能否基于样本直接确定w ?训练样本集决策规则:判别函数决策面方程选择最佳准则6一.参数估计与非参数估计参数估计:先假定研究问题具有某种数学模型,如正态分布,二项分布,再用已知类别的学习样本估计里面的参数。
非参数估计:不假定数学模型,直接用已知类别的学习样本先验知识估计数学模型。
§3-1 参数估计与监督学习13¾估计量:样本集的某种函数f (X),X ={X 1, X 2 ,…, X N }¾参数空间:总体分布未知参数θ所有可能取值组成的集合(Θ)12ˆ(,,...,)N d θθ=x x x 的()是样本集的函数,它对样本集的一次实现估计称计量点估为估计值¾点估计的估计量和估计值§3-2 参数估计理论14¾估计量评价标准: 无偏性,有效性,一致性–无偏性:E ( )=θ–有效性:D ( )小,估计更有效–一致性:样本数趋于无穷时,依概率趋于θ:ˆθˆlim ()0N P θθε→∞−>=ˆθˆθ15最大似然估计计算方法•Maximum Likelihood (ML)估计–估计参数θ是确定而未知的,Bayes 估计方法则视θ为随机变量。

第3章基本概念本章介绍机器学习中的常用概念,包括算法的分类,算法的评价指标,以及模型选择问题。
按照样本数据是否带有标签值,可以将机器学习算法分为有监督学习与无监督学习。
按照标签值的类型,可以将有监督学习算法进一步细分为分类问题与回归问题。
按照求解的方法,可以将有监督学习算法分为生成模型与判别模型。
比较算法的优劣需要使用算法的评价指标。
对于分类问题,常用的评价指标是准确率;对于回归问题,是回归误差。
二分类问题由于其特殊性,我们为它定义了精度与召回率指标,在此基础上可以得到ROC曲线。
对于多分类问题,常用的评价指标是混淆矩阵。
泛化能力是衡量有监督学习算法的核心标准。
与模型泛化能力相关的概念有过拟合与欠拟合,对泛化误差进行分解可以得到方差与偏差的概念。
正则化技术是解决过拟合问题的一种常见方法,在本章中我们将会介绍它的实例-岭回归算法。
3.1算法分类按照样本数据的特点以及求解手段,机器学习算法有不同的分类标准。
这里介绍有监督学习和无监督学习,分类问题与回归问题,生成模型与判别模型的概念。
强化学习是一种特殊的机器学习算法,它的原理将在第20章详细介绍。
3.1.1监督信号根据样本数据是否带有标签值(label),可以将机器学习算法分成有监督学习和无监督学习两类。
要识别26个英文字母图像,我们需要将每张图像和它是哪个字符即其所属的类别对应起来,图像的类别就是标签值。
有监督学习(supervised learning)的样本数据带有标签值,它从训练样本中学习得到一个模型,然后用这个模型对新的样本进行预测推断。
样本由输入值与标签值组成:(),y x其中x为样本的特征向量,是模型的输入值;y为标签值,是模型的输出值。
标签值可以是整数也可以是实数,还可以是向量。
有监督学习的目标是给定训练样本集,根据它确定映射函数:()y f=x确定这个函数的依据是它能够很好的解释训练样本,让函数输出值与样本真实标签值之间的误差最小化,或者让训练样本集的似然函数最大化。





第三章 线性分类器 (Linear Classifiers)我们看到,在一定条件下,基于概率或概率密度的分类器设计问题,即基于后验概率或类条件概率密度的分类器设计问题,或用Bayes 决策理论设计的分类器可转化为线性分类器。
线性分类器的特点是结构简单,计算工作量小,缺点是在很多情况下分类正确率不够高。
3.1 线性判别函数和决策超平面(Linear DiscriminantFunctions and Decision Hyperplanes)我们先考虑两类问题和线性判别函数。
设特征空间维数为m ,即x ∈R m ,一个超平面决策方程可写为())1.3(0:0=+=w l πT x w x这里,w =(w 1,w 2,⋯,w m )T 为权值向量,w 0为阈值(bias)。
如果x 1、x 2两个点均在超平面π上,则有)2.3(00201=+=+w w T T x w x w或())3.3(021=-x x w T显然,w 与x 1-x 2垂直。
有时,人们称w 为超平面π的法矢量。
将(3.1)展开得())4.3(0:002211==++++=∑=mi i i m m x w w x w x w x w l π x这里,x 0=1。
平面π在坐标轴上的截距为)5.3(0ii w w θ-=x 110w图3.1a 线性分类器决策超平面示意图1x 11图3.1b 线性分类器决策超平面示意图2图3.1给出了线性分类器决策超平面示意图。
根据该图,坐标原点到决策平面π的Euclid 距离为)6.3(202222100w w w w w w d m=+++=特征空间任意一点x =(x 1,x 2,⋯,x m )T 到决策平面π的Euclid 距离为()())7.3(,22222102211w x x l w w w w x w x w x w x w πd mm m i i =+++++++++=特别需要注意的是,π1: l (x )=w 1x 1+w 2x 2+⋯+w m x m +w 0=0与π2: l (x )= -w 1x 1-w 2x 2-⋯-w m x m -w 0=0所决定的平面完全相同,但它们的决策区域却是完全相反的。
《模式识别与机器学习》教学大纲Pattern Recognition and Machine Learning第一部分大纲说明1. 课程代码:2. 课程性质:学位必修课3. 学时/学分:40/34. 课程目标:模式识别与机器学习研究计算机识别物体的机理,该课程的学习将为数据分析与处理以及人工智能等领域的学习打下基础。
本课程主要分为两大部分,第一部分主要介绍模式识别,包括模式识别的基本概念、基本原理、典型方法、实用技术以及有关研究的新成果,其目的是使学生掌握模式识别的基本概念和基本原理,了解模式识别在图像分析、语音识别和音频分类等领域的具体应用、存在的问题和发展前景。
第二部分主要介绍机器学习,包括多项式回归、正则方程、逻辑回归、神经网络、深度置信网络、卷积神经网络等,通过教学使学生掌握机器学习的基础理论,以及无监督学习和强化学习等;熟悉常见机器学习的常用算法,以及算法的主要思想和运用方法,并通过编程实践和典型应用实例加深了解。
5. 教学方式:课堂讲授、自学与讨论、课堂上机与实例项目相结合6. 考核方式:考试7. 先修课程:概率论、数字信号处理9. 教材及教学参考资料:(一)教材:《模式识别》第4版,Sergios T等编,电子工业出版社边肇祺,张学工等编著,《机器学习》,Peter Flach. 人民邮电出版社, 2016.(二)教学参考资料:[1]《模式分类》(英文版·第2版), Richard O等编,机械工业出版社[2]《模式识别导论》,范九伦等编,西安电子科技大学出版社[3]《模式识别》第2版,边肇祺等编,清华大学出版社[4]《神经网络与机器学习(英文版·第3版)》. Haykin S. 机械工业出版社[5]《Deep Learning》. Ian Goodfellow, Yoshua Bengio and Aaron Courville. MIT Press第二部分教学内容和教学要求上篇模式识别第一章绪论教学内容:1.1模式与模式识别1.2模式识别的主要方法1.3监督模式识别与非监督模式识别1.4模式识别系统举例1.5模式识别系统的典型构成教学要求:了解模式识别的相关常识与概念,以及一些常用的研究方法。
判别函数分析dfa由于样本特征空间的类条件概率密度的形式常常很难确定,利用非参数方法估计需要很大的样本空间,而且随着特征空间位数的增加所需的样本数急剧增加,因此在实际问题中,我们往往不确定某个判别函数类,然后利用样本集确定出判别函数中的未知参数。
线性判别线性判别函数法是一种较为简单的判别函数,最简单的是线性函数,它的分界面是超平面,采用线性判别函数所产生的错误率或风险虽然可能比贝叶斯分类器来的大,但是他简单,容易实现,而且需要的计算量和存储量小。
因此可以认为线性判别函数是统计模式识别的基本方法之一。
模式识别系统的主要作用,判别各个模式所属的类别,对一个两类问题的判别,就是将模式x划分成ω1和ω2两类。
用判别函数分类的概念两类问题的判别函数(以二维模式样本为例)若x是二维模式样本x=(x1x2)T,用x1和x2作为坐标分量。
这时,若这些分属于ω1和ω2两类的模式可用一个直线方程d(x)=0来划分d(x)=w1x1+w2x2+w3=0其中x1、x2为坐标变量,w1、w2、w3为参数方程,则将一个不知类别的模式代入d(x),有若d(x)>0,则x属于w1若d(x)<0,则x属于w2此时,d(x)=0称为判别函数。
用判别函数进行模式分类依赖的两个因素用判别函数进行模式分类依赖的两个因素(1)判别函数的几何性质:线性的和非线性的函数。
线性的是一条直线;非线性的可以是曲线、折线等;线性判别函数建立起来比较简单(实际应用较多);非线性判别函数建立起来比较复杂。
(2)判别函数的系数:判别函数的形式确定后,主要就是确定判别函数的系数问题。
只要被研究的模式是可分的,就能用给定的模式样本集来确定判别函数的系数。
第三章判别函数与确定性分类器引言♦第二章主要讨论了在概率密度或概率函数的基础上设计分类器。
在有些情况下,分类器等价于一组线性判别函数。
♦本章主要讨论线性分类器的设计,最主要的是了解它在模式识别技术中所处的地位。
这种方法绕过统计分布状况的分析,绕过参数估计这一环,而对特征空间实行划分,称为非参数判别分类法,即不依赖统计参数的分类法。
这是当前模式识别中主要使用的方法,并且涉及到人工神经元网络与统计学习理论等多方面,是本门课最核心的章节之一。
线性分类器主要的优点是简单和可计算性。
♦从这一章起,假设来自于已知类的所有特征向量都可以用线性分类器正确分类,我们将研究相应的线性函数的计算方法,然后讨论更一般问题。
对于不能将所有向量正确分类的线性分类器,我们寻找通过采用应的优化规则设计最优线性分类器的方法。
♦贝叶斯方法与线性、非线性分类器的关系与比较图4.1理想的概率分布♦ 学习这一章要体会模式识别中以确定准则函数并实现优化的计算框架。
第一节 线性判别函数与广义线性判别函数判别函数有线性和非线性之分,而非线性判别函数又可以转化为线性形式,故首先讨论线性判别函数。
一、 两类判别问题假定有1ω和2ω两类模式,在二维模式特征空间,可用一直线将其分开,如图3—1—1所示。
假定这一直线方程为d(x )=1250x x +-=,那么很明显,凡使d(x )>0的模式i x 必属于1ω类;反之,使d(x )<0的模式i x 必属于2ω类。
于是将d(x )=125x x +-作为判别函数。
一般说来,这种将直线作为界线的判别函数的形式为:式中,i w 为参数,1x 、2x 为模式样本的特征值。
,将此判别函数推广到n 维,且用向量12(,,...,)T n x x x =x 表示模式样本,则有内积形式12()n +...++n n 2d w x w w w x x x +=+11 (3-1-2)T 0n w w x +=+1式中w =)(,,...,T l w w w 12叫权向量,w 0是阈值,若将x 和w 写成增广向量,则121(,,...,,)T n n w w w w +=w ,12(,,...,,1)T n x x x =x则式(3-1-2)可以写成更简练的形式()d T x w x = (3-1-3)判别函数及决策超平面在n 维特征空间中,在线性可分得情况下,决策超曲面是一个超平面。