夫琅禾费圆孔衍射公式
- 格式:docx
- 大小:3.66 KB
- 文档页数:2
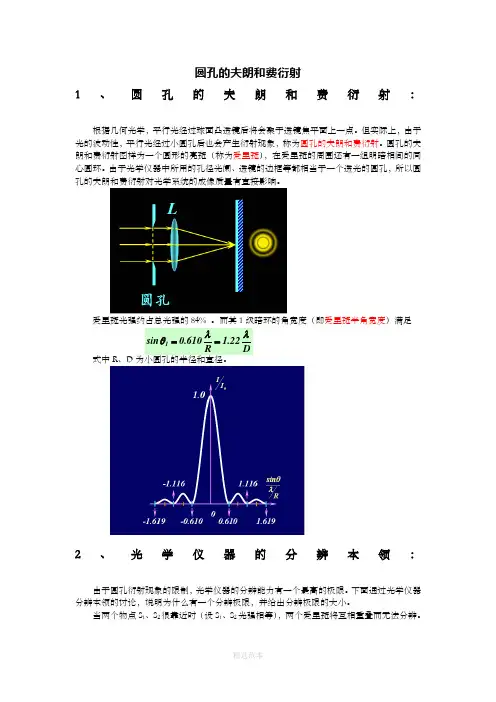
圆孔的夫朗和费衍射1、圆孔的夫朗和费衍射:根据几何光学,平行光经过球面凸透镜后将会聚于透镜焦平面上一点。
但实际上,由于光的波动性,平行光经过小圆孔后也会产生衍射现象,称为圆孔的夫朗和费衍射。
圆孔的夫朗和费衍射图样为一个圆形的亮斑(称为爱里斑),在爱里斑的周围还有一组明暗相间的同心圆环。
由于光学仪器中所用的孔径光阑、透镜的边框等都相当于一个透光的圆孔,所以圆孔的夫朗和费衍射对光学系统的成像质量有直接影响。
爱里斑光强约占总光强的84% 。
而其1级暗环的角宽度(即爱里斑半角宽度)满足D 22.1R610.0sin 1λλθ==式中R 、D 为小圆孔的半径和直径。
2、光学仪器的分辨本领:由于圆孔衍射现象的限制,光学仪器的分辨能力有一个最高的极限。
下面通过光学仪器分辨本领的讨论,说明为什么有一个分辨极限,并给出分辨极限的大小。
当两个物点S 1、S 2很靠近时(设S 1、S 2光强相等),两个爱里斑将互相重叠而无法分辨。
对一个光学仪器来说,若一个点光源产生的爱里斑的中央刚好与另一个点光源产生的爱里斑瑞的1级暗环相重合,这时两个爱里斑重合部分的光强约为单个爱里斑中央光强的80%左右,一般人眼刚好能分辨出这是两个光点的像。
因此,满足上述条件的两个点光源恰好能被该光学仪器所分辨。
这一条件称为瑞利分辨判据。
(见下图)恰能分辨时两光源发出的光线对透镜光心的夹角Δθ 称为最小分辨角,用δθ表示。
由上讨论可知,最小分辨角δθ等于爱里斑的半角宽度θ1:)D 22.1arcsin(1λθδθ==尤其当θ1 ~ 0D 22.1λδθ≈(或称分辨率),用R 表示:λδθ22.1D 1R ==讨论:⑴ 增大透镜的直径D 可提高镜头的分辨率。
光学天文望远镜的镜头孔径可达数米! ⑵ 设r 、d 为爱里斑的半径和直径,则:f 2d f r D 22.1===λδθ即:D f44.2d λ=f D称为镜头的相对孔径(越大越好)。
如照相机镜头上所标示的502:1字样,即表示镜头的焦距mm 50f =,而镜头的孔径mm 25D =。





光学光的衍射现象及衍射公式解析光学领域是研究光的传播、干涉和衍射等现象的学科。
光的衍射现象是光学中一项重要的现象,它是光通过一个或多个孔或物体后所产生的偏离直线传播方向的现象。
在本文中,我们将详细介绍光的衍射现象以及相关的衍射公式。
一、光的衍射现象光的衍射现象是由于光传播过程中的波动性导致的。
当光通过一个孔或物体时,由于它的衍射现象,光束会出现偏折和扩散。
这种现象可以用两个经典的衍射实验来进行说明。
1. 杨氏双缝干涉实验杨氏双缝干涉实验是用来观察光的衍射现象的经典实验之一。
在实验中,一束单色光通过两个相邻的狭缝,然后在屏幕上形成一系列交替的明暗条纹。
这些条纹是由光波传播过程中的衍射现象引起的,通过观察这些条纹的位置和间距,我们可以研究光的波长和干涉特性。
2. 单缝衍射实验单缝衍射实验也是常用的观察光的衍射现象的实验之一。
在实验中,一束单色光通过一个狭缝后,在屏幕上形成一个中央亮度较大的主极大,以及两侧亮度逐渐减弱的次级极大。
这些亮度的变化是由光波经过狭缝后形成的波前衍射引起的。
二、光的衍射公式光的衍射现象可以用一些数学公式来描述和分析。
在实际应用中,我们常用的两个衍射公式是夫琅禾费衍射公式和菲涅尔衍射公式。
1. 夫琅禾费衍射公式夫琅禾费衍射公式是用来描述光通过一个狭缝或一个圆孔后的衍射现象的公式。
根据夫琅禾费衍射公式,通过一个狭缝或圆孔的光衍射角度与光的波长和狭缝(或圆孔)的尺寸有关。
2. 菲涅尔衍射公式菲涅尔衍射公式是用来描述光通过一个平面透光物体后的衍射现象的公式。
通过菲涅尔衍射公式,我们可以计算出经过平面透光物体后的光的强度分布,并且可以通过调整物体的形状和尺寸来控制光的传播和衍射特性。
三、应用与研究通过对光的衍射现象和衍射公式的研究,人们可以更好地理解和应用光学现象。
在实际生活和工业应用中,光的衍射现象广泛应用于光学显微镜、光学成像、光纤通信等领域。
同时,光的衍射现象也是研究光波性质和计算光传播的基础之一。

《光学》考试公式参考一、光的干涉1.单色平面波表达式: 2.双光束干涉光强公式: , 若021I I I ==,则 3.干涉极大: ,( j = 0, ±1, ± 2, ± 3…) 4.干涉极小: 5.杨氏干涉实验光程差: 6.等倾干涉与等厚干涉的光程差: 或 7.垂直入射时等厚干涉的光程差: 8.牛顿环第j 个暗环半径: 二、光的衍射1.菲涅耳半波带法: 2.菲涅耳衍射(圆孔):波带总数 3.单缝的夫琅禾费衍射: , , 极小(暗纹)位置: , , 中央明纹条纹宽度: 4.圆孔的夫琅禾费衍射:爱里斑第一极小的角半径 5.平面衍射光栅:光线斜入射时的光栅方程6.平面光栅衍射光强分布: , 7.光栅的色分辨本领: 自由光谱范围: 角色散率: 三、几何光学的基本原理 1.单个球面的反射和折射成像 2.垂轴放大率: 四、光的偏振 1.合成光波的光矢量末端轨迹方程: , 2.马吕斯定律: 布儒斯特角: 3.波晶片 ─ 相位延迟: 4.偏振光的干涉: ])(cos[),(011111ϕυω+-=r t A t P E cos 22121ϕ∆I I I I I ++=2cos 420ϕ∆I I =)()(020*******ϕϕϕϕϕ-+-=-=r n r n k ∆ , 2πϕj =∆λδj r r n =-=)(12 , )12(πϕ+=j ∆2)12()(12λδ+=-=j r r n 012tg sin r yd d d r r ⋅=≈≈-=θθδ2cos 2202λδ-=i d n 2sin 21221220λδ--=i n n d )(22002d d n δλδ=-≈jjR r j ∝=λ()()[]k k k a a P A 11121+-+=⎪⎪⎭⎫⎝⎛+=+=0220011r R Rr r R k λρρλθtan 'f x =20sin ⎪⎪⎭⎫ ⎝⎛=ββI I P θλπθβsin sin 2b b k == sin πλθπβj b ±== sin λθj b ±= 3,2,1=j bλθθ2210≈=∆Dλθθ22.1sin 11=≈λθθj d =±)sin (sin 0220sin sin sin ⎪⎭⎫ ⎝⎛⋅⎪⎪⎭⎫ ⎝⎛=ααββN I I p 单θλπϕαsin 2⋅==d ∆N j A ||=≡δλλjF λλ=∆θδλθδθcos 1d j D ==rnn s n s n -'=-''sn s n y y ''='=βϕϕ∆∆22222sin cos 2=-+y x y x yy x x A A E E A E A E xy ϕϕϕ-=∆α212cos I I =2112tg n n n i B ==d n n e o x y )(2-=-=λπϕϕϕ∆cos 22222222ϕ∆e o e o A A A A A I ++==。




课程名称:物理光学实验
实验名称:夫琅禾费衍射实验
'0'0E()a a P C C ==⎰⎰,利用贝塞尔
消像差透镜
图4 夫琅禾费衍射光路图
使其探测面与透镜的距离为透镜焦距f(探测器靶面的位置与滑块
17.3mm,透镜距离滑块刻度为6mm);
“相机图像”预览功能,预览衍射图案。
调整CCD
光强适中(不饱和,也不过弱)。
记录CCD处的衍射图案;
打开软件,点击“圆孔方孔衍射”→“捕获衍射图案”,获取夫琅禾费圆孔衍射的实
图5
图6
图7 图8
图9 2.当D=300μm时的夫琅禾费圆孔衍射
图10
图11 图12
图13 L=500μm时的夫琅禾费方孔衍射
图14
图16
图17 L=300μm时的夫琅禾费方孔衍射
图18
图19 图20
图21
六、数据处理
同数据记录
七、结果陈述:
实验得到了夫琅禾费圆孔衍射和夫琅禾费方孔衍射的实验图像。
测量了夫琅禾费圆孔衍射和夫琅禾费方孔衍射的光强分布,发现实验值和理论值符合的很好,说明夫琅禾费衍射公式的正确性。
实验得到了夫琅禾费圆孔衍射和夫琅禾费方孔衍射虚焦时的图像。
“圆孔夫琅禾费衍射”课程设计指南孙伟 燕山大学应用物理系1. Maxwell 方程组和电磁波十八世纪中叶,James Maxwell 将已知的各种电磁作用关系用一组方程组合起来,形成了一个方程组:E ερ=⋅∇ (源于库伦定律的高斯定律) (1.1) 0=⋅∇B (源于毕奥-萨瓦尔定律的高斯定律) (1.2)t ∂∂-=⨯∇BE (法拉第定律) (1.3) J EB 000μεμ+∂∂=⨯∇t(Maxwell 修正的安培定律) (1.4)式中,E 和B 分别代表了电场和磁场分量。
电荷密度ρ描述空间单位体积内的电荷量分布;电流密度J 描述电荷的移动(单位体积电荷乘以速度)。
0ε表示真空介电常数,其值为()2212010854.8m N C ⋅⨯=-ε。
0μ表示真空磁导率,其值为A m T .10470-⨯=πμ(或者2C m kg ⋅)。
在安培定律中引入了一个关键参数之后,Maxwell 意识到,方程组构成了一个完美的电磁现象自洽理论。
此外,方程组预言了电磁波的存在,并以光速传播。
在Maxwell 时代之前就已经有人对光速进行了测量,因此一个显而易见的结果(当时还难以令人置信)便是,光是一种高频振荡。
而在此之前,光学还仍然作为一种独立于电学和磁学的主体进行讨论的。
2. 波动方程当Maxwell 统一了电磁理论以后,他马上意识到,波动可能是该方程组的解的形式。
事实上,他希望找到一组满足波动形式的方程组,以辅助他完成找到真正的波动方程。
既然已经知道了光是以波动方式传播的,基尔霍夫首先注意到了001εμ正好给出了精确的光速c = 3.00×108m / s (之前就已经被测量过),并且法拉第和克尔已经观测到强磁场和强电场会影响光在晶体中的传播。
对初接触Maxwell 方程组的人来说,并不能一眼就看出它的解具有波动形式。
但是经过适当的数学操作,我们就可以将它变为波动方程的形式。
我们来推导电场E 的波动方程,磁场B 的波动方程的推导过程是类似的。
实验十五 夫琅和费圆孔衍射实验目的1、了解圆孔的夫琅和费衍射现象。
2、掌握用衍射测圆孔的直径的方法。
实验装置(图15-1) 1:钠灯2:小孔(φ1mm ) 3:衍射孔(φ0.2-0.5mm ) 4:三维调节干版架 (SZ-18)7:测微目镜8:光源二维调节架 (SZ-19) 9:三维平移底座(SZ-01) 10:二维平移底座(SZ-02)衍射图样为图15-3:图15-3经理论推导的衍射的光强分布为:210))(2(mm J I I =λθπ=/sin 2a m ,是一阶贝塞耳函数。
)(1m J 圆孔衍射的第一暗纹的条件:aλ=θ61.0sin 则中央零级亮纹斑(爱里斑)的角半径:a /61.0λ≈θΔ线半径:f a l′⋅λ=/61.02爱里斑的直径:λ′=af e 22.1实验中,已知波长,透镜焦距οA 5893=λf ′,圆孔半径a ,用测微目镜测出爱里斑的直径,从而验证公式λ′=af e 22.1实验内容1、调整光路,调节衍射条纹。
2、用测微目镜则出爱里斑的直径。
3、验证公式λ′=a f e 22.14、改变圆孔的半径a ,进一步测量和验证。
实验步骤1)参照图15-1沿平台米尺安排各器件,调节共轴,获得衍射图样。
2)在黑暗环境用测微目镜测量艾里斑的直径e ,据已知波长(λ=589.3nm )、衍射小孔半径a 和物镜焦距f’,可验证公式λaf e '22.1=实验注意事项1、圆孔不能太大。
2、观察在焦平面上观察。
3、测圆斑的直径时圆心要选准并两边相切。
4、测量时要避免回程误差。
实验讨论思考题1、请证明圆孔的夫琅和费衍射的光强分布为:210))(2(mm J I I = 2、当圆孔直径增大或减小时,衍射条纹如何变化? 3、当入射光的波长改变时,衍射条纹如何变化? 4、如果透镜L 不放,衍射结果如何?实验十六 菲涅耳单缝衍射观察和分析实验目的1、了解菲涅耳衍射的条件及观察。
2、了解菲涅耳衍射和夫琅和费衍射的转化。
夫琅禾费圆孔衍射公式
夫琅禾费圆孔衍射公式是描述光线通过一个圆孔时的衍射现象的数学公式。
它可以用来计算衍射光的强度分布情况,进一步揭示光的波动性质。
本文将介绍夫琅禾费圆孔衍射公式的基本原理和应用。
夫琅禾费圆孔衍射公式的原理是基于惠更斯-菲涅尔原理和赫兹积分定理。
根据这两个原理,我们可以将一个圆孔近似看作无数个点光源的叠加,每个点光源都是由圆孔上的每一点发出的球面波。
当这些球面波在远离圆孔时相互叠加时,形成了一种干涉现象,即衍射现象。
夫琅禾费圆孔衍射公式的表达形式为:
I(θ) = I_0 * (J1(α) / α)^2
其中,I(θ)表示在θ方向上的光强分布,I_0表示中央峰的光强,J1(α)表示第一类贝塞尔函数,α表示无量纲的衍射角,其定义为α = (π * a * sin(θ)) / λ,其中a为圆孔半径,λ为入射光的波长。
夫琅禾费圆孔衍射公式告诉我们,光强的分布与衍射角有关。
当衍射角较小时,即光线以近似平行的方式射向圆孔时,衍射现象不明显,光强分布呈现出一个中央峰和一些弱的旁边峰。
随着衍射角的增大,中央峰逐渐减弱,旁边峰逐渐增强,最终形成一系列的衍射环。
夫琅禾费圆孔衍射公式的应用非常广泛。
首先,它可以用来解释和预测光通过圆孔时的衍射现象。
例如,在天文学中,我们可以利用夫琅禾费圆孔衍射公式来研究星光经过望远镜的衍射效应,从而探测和测量天体的角直径。
其次,夫琅禾费圆孔衍射公式也可以应用于光学元件的设计和优化。
例如,在激光技术中,我们可以根据夫琅禾费圆孔衍射公式来设计和调整光束的直径和光强分布,以满足实际应用需求。
此外,夫琅禾费圆孔衍射公式还可以应用于其他领域,如光学信息处理、光学显微镜等。
除了夫琅禾费圆孔衍射公式,还有其他一些相关的衍射公式和现象,如多孔衍射、狭缝衍射等。
这些公式和现象都是研究光的波动性质和光与物质相互作用的重要工具。
通过深入研究这些公式和现象,我们可以更好地理解和应用光学原理,推动光学科学和技术的发展。
夫琅禾费圆孔衍射公式是描述光线通过一个圆孔时的衍射现象的数学公式。
它基于惠更斯-菲涅尔原理和赫兹积分定理,可以用来计算衍射光的强度分布情况。
夫琅禾费圆孔衍射公式在光学研究和应用中具有重要的地位和作用,对于理解和利用光的波动性质具有重要意义。
通过进一步研究和应用,我们可以更好地探索和发展光学科学和技术。