对称型电感模型及并联选取技巧
- 格式：doc
- 大小：1.78 MB
- 文档页数：7
下载文档原格式
合集下载
电感串联和并联.24页PPT
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
电感串联和并联.
1、战鼓一响，法律无声。——英国 2、任何法律的根本；不，不成文法本 身就是 讲道理 ……法 律，也 ----即 明示道 理。— Nhomakorabea爱·科 克
3、法律是最保险的头盔。——爱·科 克 4、一个国家如果纲纪不正，其国风一 定颓败 。—— 塞内加 5、法律不能使人人平等，但是在法律 面前人 人是平 等的。 ——波 洛克
（整理）IGBT并联技术详解.
（整理）IGBT并联技术详解.IGBT并联技术技术详解IGBT并联均流问题影响静态均流的因素1、并联IGBT的直流母线侧连接点的电阻分量，因此需要尽量对称；2、IGBT芯⽚的Vce(sat)和⼆极管芯⽚的V F的差异，因此尽量采取同⼀批次的产品。
3、IGBT模块所处的温度差异，设计机械结构及风道时需要考虑；4、IGBT模块所处的磁场差异；5、栅极电压Vge的差异。
影响动态均流的因素1、IGBT模块的开通门槛电压VGEth的差异，VGEth越⾼，IGBT开通时刻越晚，不同模块会有差异；2、每个并联的IGBT模块的直流母线杂散电感L的差异；3、门极电压Vge的差异；4、门极回路中的杂散电感量的差异；5、IGBT模块所处温度的差异；6、IGBT模块所处的磁场的差异。
IGBT芯⽚温度对均流的影响IGBT芯⽚的温度对于动态均流性能和静态均流性能影响很⼤：1、由于IGBT的Vcesat的正温度系数特性，使温度⾼的芯⽚的Vcesat更⾼，会分得较少的电流，因此形成了⼀个负反馈，使静态均流趋于收敛；2、根据我们的经验，我们发现，芯⽚温度变⾼后，动态均流的性能也会变好；例如在测试动态均流时，我们会使⽤双脉冲测试⽅法，但这时芯⽚是处于冷态的，当把机器跑起来后，动态均流会改善。
IGBT芯⽚所处的磁场对均流的影响IGBT模块附近如果有强磁场，则模块的均流会受到影响。
1、如果两个IGBT模块并联且并列安装，如果交流排的输出电缆在摆放时靠近其中某⼀个IGBT模块⽽远离另外⼀个，则均流性能就会出问题；2、以上现象的原因是某个⼤电流在导线上流动时会产⽣磁场，对磁场内的其他导通的电流产⽣“挤出”或“吸引”的效应；因此，在结构设计时，需要注意交流排出线的⾛线形式，以免发⽣磁场的⼲涉现象。
IGBT并联使⽤⽅法分类IGBT并联可以分为“硬并联”及“桥臂并联”2⼤类。
（1）“硬并联”指的是IGBT的发射极和集电极直接连接在⼀起，如左下图所⽰；（2）“桥臂并联”指的是，IGBT桥臂的交流输出端通过均流电抗（感量有⼀定数值）连接在⼀起，如右下图所⽰；这两种分类⽅法本质上以模块交流端⼦到汇流端的电感量进⾏分类的。
并联高抗中性点小电抗补偿原理分析及参数选择方法
并联高抗中性点小电抗补偿原理分析及参数选择方法 并联高抗中性点接小电抗四线补偿的思想是通过对导线相间电容的补偿来隔离相间联系，削弱潜供电流与恢复电压的电容性分量，此时小电抗进行的是二次补偿。
在系统不同的运行情况下，小电抗器参数选择的原则和方法也不相同。
2.1 等值电源定理分析小电抗二次补偿高抗中性点加小电抗四线补偿原理示意图见图1-4。
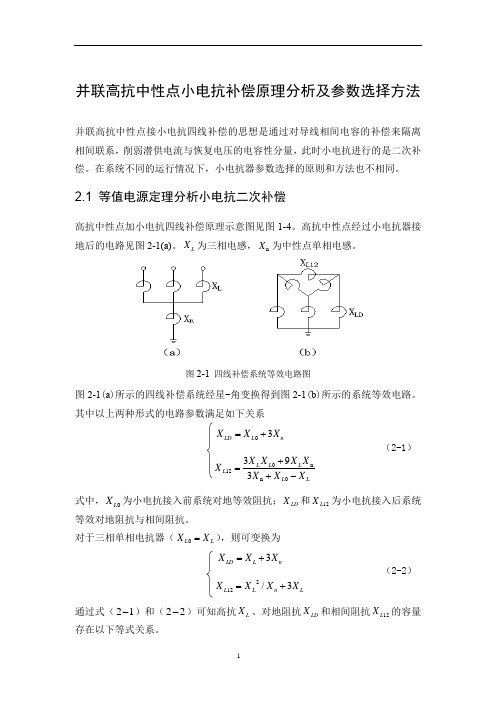
高抗中性点经过小电抗器接地后的电路见图2-1(a)。
L X 为三相电感，n X 为中性点单相电感。
图2-1 四线补偿系统等效电路图图2-1(a )所示的四线补偿系统经星-角变换得到图2-1(b )所示的系统等效电路。
其中以上两种形式的电路参数满足如下关系n L LD X X X 30+=L L L L L L X X X X X X X X -++=0n n 012393式中，0L X 为小电抗接入前系统对地等效阻抗；LD X 和12L X 为小电抗接入后系统等效对地阻抗与相间阻抗。
对于三相单相电抗器（L L X X =0），则可变换为n L LD X X X 3+= L n L L X X X X 3/212+= 通过式（12-）和（22-）可知高抗L X 、对地阻抗LD X 和相间阻抗12L X 的容量存在以下等式关系。
（2-1） （2-2）L N L N LD N X U X U X U 21222)3(=+ （2-3）由式（2-3）可知，高抗的容量等于对地电抗和相间电抗的容量之和，小电抗的投入并未改变实际的补偿容量，其所起的作用只是令高抗的容量合理的分配至相间与相对地两部分。
小电抗器n X 的投入，其作用是等效产生了相间感抗来补偿导线相之间电容，而高抗只是补偿回路的对地电容，故小电抗进行的是二次补偿[1,7]。
单回线路高抗中性点接小电抗器主要是为了限制容性分量潜供电流，其流通回路如图2-2（a ）所示，应用等值电源定理，可简化得到图2-2（b ）所示的单相等值电路。
对称的三相电源和对称的三相负载连接
解 （ 1 ） 由于电动机的额定电压为 220 V ，与电源的相 电压相等，因此电动机定子绕组作星形连接。 （2） 线电压UUV 的相量： =380∠30° V 根据三相电源Y形连接时线电压和相电压的关系可知
线电流相量表达式为：
其瞬时傎表达式为： iU =22sin (ω t-53.13°) A 由于iU 、iV 、iW 为三相对称电流，因此根据对称关 系， 得
◆波形图：
如图5-1-2所示
◆相量表达式为：
◆对应的相量图：如图3所示
很明显，根据KVL，对称三相电动势的瞬时值或相量之和为零，
即：
三相交流电依次达到正最大值（或相应零值）的顺 序称为相序（phase sequence）。上述对称三相电动势的 相序是U→V→W。把U→V→W的相序称为顺相序（positive sequence），通常都是采用顺相序。 在三相绕组中，把哪一个绕组当作U相绕组是无关紧 要的，但U相绕组确定后，电动势比 eU滞后120°的绕组 就是V相，电动势比eU滞后240°（超前120°）的那个绕 组则为W相。
1．三相电源的星形（Y形）连接
• 图5-1-3是三相电源的Y形连接。
图 5-1-3
把端线与中线之间的 电压uU、uV、uW称为相电 压。 规定相电压的参考方 向是从端线指向中线， 如图5-1-3所示。 很显然， 如果不考 虑输电线上的压降和三相 绕组的内阻抗， 相电压 uU 、uV、uW就分别等于eU 、 e V 、 eW ， 即
如果将某一相绕组接反，闭合回路中就有大于相电
压的电压在作用，由于三相电源绕组本身内阻抗很小，故 在闭合回路中产生很大的电流，会烧坏三相电源绕组。通 常三相发电机的三相绕组均作 Y形连接，很少作D 形连接， 而三相变压器则两种接法都有使用。
线电流相量表达式为：
其瞬时傎表达式为： iU =22sin (ω t-53.13°) A 由于iU 、iV 、iW 为三相对称电流，因此根据对称关 系， 得
◆波形图：
如图5-1-2所示
◆相量表达式为：
◆对应的相量图：如图3所示
很明显，根据KVL，对称三相电动势的瞬时值或相量之和为零，
即：
三相交流电依次达到正最大值（或相应零值）的顺 序称为相序（phase sequence）。上述对称三相电动势的 相序是U→V→W。把U→V→W的相序称为顺相序（positive sequence），通常都是采用顺相序。 在三相绕组中，把哪一个绕组当作U相绕组是无关紧 要的，但U相绕组确定后，电动势比 eU滞后120°的绕组 就是V相，电动势比eU滞后240°（超前120°）的那个绕 组则为W相。
1．三相电源的星形（Y形）连接
• 图5-1-3是三相电源的Y形连接。
图 5-1-3
把端线与中线之间的 电压uU、uV、uW称为相电 压。 规定相电压的参考方 向是从端线指向中线， 如图5-1-3所示。 很显然， 如果不考 虑输电线上的压降和三相 绕组的内阻抗， 相电压 uU 、uV、uW就分别等于eU 、 e V 、 eW ， 即
如果将某一相绕组接反，闭合回路中就有大于相电
压的电压在作用，由于三相电源绕组本身内阻抗很小，故 在闭合回路中产生很大的电流，会烧坏三相电源绕组。通 常三相发电机的三相绕组均作 Y形连接，很少作D 形连接， 而三相变压器则两种接法都有使用。
(整理)IGBT并联技术详解.
IGBT并联技术技术详解IGBT并联均流问题∙影响静态均流的因素1、并联IGBT的直流母线侧连接点的电阻分量，因此需要尽量对称；2、IGBT芯片的Vce(sat)和二极管芯片的V F的差异，因此尽量采取同一批次的产品。
3、IGBT模块所处的温度差异，设计机械结构及风道时需要考虑；4、IGBT模块所处的磁场差异；5、栅极电压Vge的差异。
∙影响动态均流的因素1、IGBT模块的开通门槛电压VGEth的差异，VGEth越高，IGBT开通时刻越晚，不同模块会有差异；2、每个并联的IGBT模块的直流母线杂散电感L的差异；3、门极电压Vge的差异；4、门极回路中的杂散电感量的差异；5、IGBT模块所处温度的差异；6、IGBT模块所处的磁场的差异。
∙IGBT芯片温度对均流的影响IGBT芯片的温度对于动态均流性能和静态均流性能影响很大：1、由于IGBT的Vcesat的正温度系数特性，使温度高的芯片的Vcesat更高，会分得较少的电流，因此形成了一个负反馈，使静态均流趋于收敛；2、根据我们的经验，我们发现，芯片温度变高后，动态均流的性能也会变好；例如在测试动态均流时，我们会使用双脉冲测试方法，但这时芯片是处于冷态的，当把机器跑起来后，动态均流会改善。
∙IGBT芯片所处的磁场对均流的影响IGBT模块附近如果有强磁场，则模块的均流会受到影响。
1、如果两个IGBT模块并联且并列安装，如果交流排的输出电缆在摆放时靠近其中某一个IGBT模块而远离另外一个，则均流性能就会出问题；2、以上现象的原因是某个大电流在导线上流动时会产生磁场，对磁场内的其他导通的电流产生“挤出”或“吸引”的效应；因此，在结构设计时，需要注意交流排出线的走线形式，以免发生磁场的干涉现象。
IGBT并联使用方法分类IGBT并联可以分为“硬并联”及“桥臂并联”2大类。
（1）“硬并联”指的是IGBT的发射极和集电极直接连接在一起，如左下图所示；（2）“桥臂并联”指的是，IGBT桥臂的交流输出端通过均流电抗（感量有一定数值）连接在一起，如右下图所示；这两种分类方法本质上以模块交流端子到汇流端的电感量进行分类的。
电感讲解及选取技巧
电感器(Inductor)是能够把电能转化为磁能而存储起来的元件。
电感器的结构类似于变压器，但只有一个绕组。
电感器具有一定的电感，它只阻碍电流的变化。
如果电感器在没有电流通过的状态下，电路接通时它将试图阻碍电流流过它；如果电感器在有电流通过的状态下，电路断开时它将试图维持电流不变。
电感器又称扼流器、电抗器、动态电抗器。
结构电感器一般由骨架、绕组、屏蔽罩、封装材料、磁心或铁心等组成。
1、骨架骨架泛指绕制线圈的支架。
一些体积较大的固定式电感器或可调式电感器（如振荡线圈、阻流圈等），大多数是将漆包线（或纱包线）环绕在骨架上，再将磁心或铜心、铁心等装入骨架的内腔，以提高其电感量。
骨架通常是采用塑料、胶木、陶瓷制成，根据实际需要可以制成不同的形状。
小型电感器（例如色码电感器）一般不使用骨架，而是直接将漆包线绕在磁心上。
空心电感器（也称脱胎线圈或空心线圈，多用于高频电路中）不用磁心、骨架和屏蔽罩等，而是先在模具上绕好后再脱去模具，并将线圈各圈之间拉开一定距离。
2、绕组绕组是指具有规定功能的一组线圈，它是电感器的基本组成部分。
绕组有单层和多层之分。
单层绕组又有密绕（绕制时导线一圈挨一圈）和间绕（绕制时每圈导线之间均隔一定的距离）两种形式；多层绕组有分层平绕、乱绕、蜂房式绕法等多种。
3、磁心与磁棒磁心与磁棒一般采用镍锌铁氧体（NX系列）或锰锌铁氧体（MX系列）等材料，它有“工”字形、柱形、帽形、“E”形、罐形等多种形状。
4、铁心铁心材料主要有硅钢片、坡莫合金等，其外形多为“E”型。
5、屏蔽罩为避免有些电感器在工作时产生的磁场影响其它电路及元器件正常工作，就为其增加了金属屏幕罩（例如半导体收音机的震荡线圈等）。
采用屏蔽罩的电感器，会增加线圈的损耗，使Q值降低。
6、封装材料有些电感器（如色码电感器、色环电感器等）绕制好后，用封装材料将线圈和磁心等密封起来。
封装材料采用塑料或环氧树脂等。
铜线圈电感是导线内通过交流电流时，在导线的内部周围产生交变磁通，导线的磁通量与生产此磁通的电流之比。
电感器的串联和并联
电感器的串联和并联
若干电感器连接成一个电路时，它们的总电感与若干电阻串并联后的总阻值相似。
当电感器之间的磁场无相互作用时，用下面的公式计算：
如果电感器的磁场之间存在耦合，那么总电感的表达式会稍微复杂一些。
对于两个电感器串联的简单情形，表达式如下：
串联电感，
L total=L1+L2±2M
式中，M为两磁场相互作用引起的互感（注意：＋M是两磁场同向的情况，-M为反向情况。
）。
串联电感，
一些LC储能电路的谐振电路使用空芯线圈，如图所示。
注意图中两相邻电感器相互垂直排列。
在具体的无线电路设计中，这样的排列虽然麻烦，但却是减少每个
磁场之间相互作用的一种方法。
一般来说，如果线圈之间非常相似，那么要遵循以下两条原则：
（1）两线圈轴线互相平行时，相互作用最大。
（2）两线圈轴线互相垂直时，相互作用最小。
当两线圈轴线沿同一条直线时，相互作用取决于两线圈之间的间距。
图 电感器之阃相互垂直地排列。
射频对称型螺旋电感优化设计
２ ｌ ２ｏ 中阖高新技书，业 ２ ｏ ０ １ 止 ＼ ９
技
电枢 电流 产 生磁 势 ， 引起磁 链 轴 分量 产 生轴 磁势 ，
术 曳引机 的转速较低 ，保证了驱动装置速度反馈的精
度 ，用 于 速度 检测 的编码 器 具有 较 高 的精度 。
测试，在给定金属线宽度和电感量前提下 ，圆形螺旋 电
感 的 电阻损 耗 最 小 ，Ｑ 最 高 ，但 是 目前 的 生产 技 术难 值
以实现圆形布线工艺，所 以多采用矩形平面螺旋 电感。
成 电路研究 的热 点和难 点。衡量集成片上螺旋 电感性
能 优 劣 的主 要 性 能 参 数 为 电感 量 Ｌ 品质 因数 Ｑ 。 由 和 值 于 硅 基 底 Ｃ Ｏ 工 艺 采 用 导 电衬底 材 料 ， 高 频 涡 流 损耗 ＭＳ
容 组 成 的 谐振 电路 ，其 谐 振 特 性不 明显 。Ｑ 的 大小 ， 值 影 响 回 路 的 选 择 性 、 效 率 、滤 波 特 性 以及 频 率 的稳 定 性 。但 提 高 线 圈 的Ｑ 应根 据 实 际使 用 场 合 、在 一 定 范 值
围 内提 高 线 圈 的Ｑ 。 值
下降的现 象；三是通 电后在硅衬底 中不可避免形成 的
射频对称型螺旋 电感优化设计
李 永 清
（ 岭 师 范 高等 专科 学校 理 工 学 院 ， 宁 铁 岭 １ ２ ０ 铁 辽 １ ０ ０）
摘要 ： 对 目前 由于射频 集 成 电路 中平 面螺 旋 电感 工 艺上的缺 陷而导致 的损 耗过 大 ，文 章通过 对 电感 线 圈品 针 质 因数 Ｑ 值 和射 频 集成 电路 螺 旋 电感 Ｑ 值 的分析 ，提 出 了对 螺旋 电感 几何 结构进 行对 称性优 化设 计 的方 案 ， 以充 分提 高射频 集成 螺旋 电感特 性 的有效 方 法。 关键 词 ： 频集 成 电路 ； 射 对称型 螺旋 电感 ； 品质 因数 ；工艺设 计 中图分 类号 ： Ｍ５２ Ｔ ５ 文献标 识码 ： Ａ 文章编 号 ： ０ ９ ２７ ２ １ ） ６ ０２ — ２ １０ — ３ ４（ ０ ０ － ０９ ０ １ 在 射 频 电路 的 设 计 中 ， 电感 和 传 输 线变 压 器 等 感 性 元 器 件 通 常 会 用 到 ， 传 统 的Ｃ Ｏ 射 频 电路 由 于 面 ＭＳ 积 、体 积 过 大会 直 接 导致 设 计 的 整 个 电路 的 面 积 、 体 积 过 大 。 随 着 电子 系 统 的 微 小 型 化 和 系 统 集 成 化 的 不 断发 展 ，射 频 收 发 电路 已实 现 Ｃ Ｏ 全 集 成 ，将 电感 设 ＭＳ 计 成 螺 旋 结 构 ，直 接 布 线 在 以硅 为主 要 材 料 的 介质 基 板 上 ，减 小 了整 个 电路 的 体 积 ，如 何 在 Ｃ Ｏ 集 成 片 上 ＭＳ 实 现 高性 能 的集 成 平 面 螺 旋 电感 的工 艺 是 目前 射 频 集 旋 线 的形状 可 以制成六 边 形 、八边 形 圆形 或矩 形 。经 过
电路中的电感器的组合与计算
电路中的电感器的组合与计算电感器是电路中重要的元件之一，它具有储存和释放能量的特性。
在复杂的电路设计中，经常需要对多个电感器进行组合和计算，以满足电路的需求。
本文将介绍电感器的组合与计算方法。
一、串联电感器的组合与计算串联电感器是指将多个电感器按照一定顺序连接在一起。
在串联连接的电感器中，电感值相加。
假设有两个串联电感器，其电感值分别为L1和L2，那么它们串联后的总电感值Ls可以通过以下公式计算得到：Ls = L1 + L2对于多个串联电感器，其总电感值可以通过递推的方式计算得到：Ls = L1 + L2 + L3 + ... + Ln二、并联电感器的组合与计算并联电感器是指将多个电感器的两端连接在一起，形成一个共同的节点。
在并联连接的电感器中，电感值的倒数之和等于总电感值的倒数。
假设有两个并联电感器，其电感值分别为L1和L2，那么它们并联后的总电感值Lp可以通过以下公式计算得到：1 / Lp = 1 / L1 + 1 / L2对于多个并联电感器，其总电感值可以通过递推的方式计算得到：1 / Lp = 1 / L1 + 1 / L2 + 1 / L3 + ... + 1 / Ln三、串并联电感器的组合与计算在实际的电路设计中，常常需要将串联和并联电感器进行组合。
这时，可以先计算出串联电感器的总电感值，再将该总电感值与其他并联电感器进行计算。
假设有两个串联电感器L1和L2，并且与它们并联的电感器L3，那么它们组合后的总电感值Lc可以通过以下公式计算得到：Lc = (L1 + L2) //并联电感器的总电感值Lp = 1 / (1 / Lc + 1 / L3) //串并联电感器的总电感值通过以上的组合与计算方法，我们可以灵活地设计和优化电路结构，以满足电路的需求。
同时，还可以根据电路中电感器的特性参数，如电感值、电流和频率等，结合实际情况进行选择和匹配。
总之，电感器的组合与计算在电路设计中起着至关重要的作用。
对称分量法及电力系统元件的各序参数和等值电路_OK
• 静止元件：正序阻抗等于负序阻抗，不等于零序 阻抗。如：变压器、输电线路等。
• 旋转元件：各序阻抗均不相同。如：发电机、电 动机等元件。
17
一、同步发电机的负序和零序电抗
1 同步发电机的负序电抗
• 负序旋转磁场与转子旋转 方向相反，因而在不同的 位置会遇到不同的磁阻 （因转子不是任意对称 的），负序电抗会发生周 期性变化。
15
E a Ia1 (ZG1 Z L1 ) Va1 0 Ia2 (ZG2 Z12 ) Va2 0 Ia0 (ZG0 Z L0 3Z n ) Va0
E 0
Ia1Z1 Va1 Ia2 Z 2 Va2
0 Ia0 Z 0 Va0
2021/8/29 16
4.2 电力系统各序网络
13
三、对称分量法在不对称短路计算中的应用 ➢ 负序网
0 Ia2 (ZG2 Z12 ) Va2
14
三、对称分量法在不对称短路计算中的应用 ➢ 零序网
Ia0 Ib0 Ic0 3Ia0
0 Ia0 (ZG0 Z L0 ) 3Ia0 Z n Va0
0 Ia0 (ZG0 Z L0 3Zn ) Va0
Xinjiang Univ ersity
第四章 对称分量法及电力系统元件的各 序参数和等值电路
1
电气工程学院 电气工程及其自动化专业
1、什么是对称分量法？ 2、为什么要引入对称分量法？
➢ 对称分量法
分析过程是什么？
1、各元件的序参数是怎样的？
➢ 对称分量法在不对称故2、障如何分绘析制电计力算系中统的的序应网图用？
Zs
Z m
Z sc
Байду номын сангаас
0
0
Z Z
s
• 旋转元件：各序阻抗均不相同。如：发电机、电 动机等元件。
17
一、同步发电机的负序和零序电抗
1 同步发电机的负序电抗
• 负序旋转磁场与转子旋转 方向相反，因而在不同的 位置会遇到不同的磁阻 （因转子不是任意对称 的），负序电抗会发生周 期性变化。
15
E a Ia1 (ZG1 Z L1 ) Va1 0 Ia2 (ZG2 Z12 ) Va2 0 Ia0 (ZG0 Z L0 3Z n ) Va0
E 0
Ia1Z1 Va1 Ia2 Z 2 Va2
0 Ia0 Z 0 Va0
2021/8/29 16
4.2 电力系统各序网络
13
三、对称分量法在不对称短路计算中的应用 ➢ 负序网
0 Ia2 (ZG2 Z12 ) Va2
14
三、对称分量法在不对称短路计算中的应用 ➢ 零序网
Ia0 Ib0 Ic0 3Ia0
0 Ia0 (ZG0 Z L0 ) 3Ia0 Z n Va0
0 Ia0 (ZG0 Z L0 3Zn ) Va0
Xinjiang Univ ersity
第四章 对称分量法及电力系统元件的各 序参数和等值电路
1
电气工程学院 电气工程及其自动化专业
1、什么是对称分量法？ 2、为什么要引入对称分量法？
➢ 对称分量法
分析过程是什么？
1、各元件的序参数是怎样的？
➢ 对称分量法在不对称故2、障如何分绘析制电计力算系中统的的序应网图用？
Zs
Z m
Z sc
Байду номын сангаас
0
0
Z Z
s
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
對稱型電感模型及並聯選取技巧Modeling of Symmetric Inductors and Selective Metal Parallel Shunting TechniqueIC 編號：D35-92A-19t指導教授：劉深淵台灣大學電機研究所教授電話：(02)23635251 ext. 239 E-mail: lsi@.tw 設計者：吳家欣博士班研究生電話：(02)23635251 ext. 326 E-mail: d0943002@.tw一、中文摘要在此計畫中提出一種利用voltage profile 的觀念來分析對稱型電感中雜散電容的問題，目前對稱型電感已廣泛應用在許多高頻差動電路上，主要是差動電路可以提供許多單端電路無法提供的優點如對共模雜訊的消除及對走線雜散效應的消除，而目前對於對稱型電感的研究很少，希望藉由此計畫提出對對稱型電感的模型及應用並聯選取的技巧來改善對稱型電感的品質因素。
AbstractIn this project, a method to shift the frequency f Qmax of maximized inductor’s quality factor Q max onto the desired frequency without additional processing steps and investigate the parasitic capacitances in the symmetric inductor. Many different-sized symmetric inductors have been implemented in 0.35µm 2P4M CMOS process to verify the theorem and the proposed method. Different circuits can afford many advantages such as common-mode noise cancellation and the immunity to parasitic effects. In this project, the modeling of parasitic capacitance in the symmetric inductor has been proposed and to improve inductor Q by means of proposed selective metal parallel shunting technique.Keywords對稱型電感，symmetric inductor，選取部份金屬並聯電感，Q值，Q-factor，f Qmax，Q max。
二、計劃緣由與目的單晶片電感(monolithic inductor)已被廣泛應用在各種射頻積體電路上，如低雜訊放大器、壓控震盪器或功率放大器等。
儘管在矽製程上實現單晶片電感常會造成其品質因數過低的問題，但現有的研究仍朝向將電感實現於晶片內以達到外部元件達到最少數目以降低成本。
射頻積體電路的特性好壞與電感的Q值有密切的關係，通常Q值越高的電感能帶給電路較好的特性。
因此如何製作在工作頻率上高Q 值的電感成為實現射頻積體電路的重要課題。
本計畫的目的在於利用標準的互補式金氧半製程實現對稱型電感及利用選取部分多層並聯技巧來改善電感的品質因素。
三、研究方法與成果3.1設計原理與方法此計畫中將使用電壓分布剖面圖(voltage profile)來分析電感中的雜散電容值。
圖一為平面式電感(planar inductor)的電壓分布剖面圖。
圖二為對稱型電感的架構圖。
圖三為對稱型電感(symmetric inductor)的電壓分布剖面圖。
由圖一及圖三推導, 電感中等效雜散C p 及C sub可以分別表示為：21112)]()1(2[41)]1()1([41kdkdACCkdkdlCCnkkmssubnkkmmp---=--+=∑∑=-=其中kkrrrrkd++++≡-121...)()/(t o tkkRRr≡由上述的式子可以知道對稱型電感其電感內等校雜散電容值會改變，但其感值卻未有很大的變化。
總的來說電感對地的雜散電容是減少的，因此對稱型電感的品質因素及自振頻率都較一般平面電感為高。
此外利用選取部份金屬並聯的方式來改變電感的等效電容值及DC 電阻值，可以將對稱型電感品質因數最高的頻率移至電路操作頻率上，來改善電路效能。
圖三為對稱型電感利用並聯選取技巧來改善對稱型電感的品質因素。
圖四簡單地圖示這樣的原理，因此在不同的操作頻率會有各自不同的最佳並聯方式。
表一所示為台積電0.35µm CMOS製程在不同金屬並聯下的特性。
藉由表一及對電壓分布剖面圖的徹底了解，一個客製化的軟體被發展出來，用來預測電感的品質因數的最大值及最大值落在的頻率。
利用所提出的方法及此客製化軟體將壓控震盪器中所使用的電感最佳化以改善相位雜訊效能。
3.3 模擬與製作在電感的模擬方面我們使用Berkeley大學所發表的ASITIC程式。
利用程式得出我們所需要的電感值和layout，再轉入Cadence複製多層並用via貫穿並聯就可以瞭解每圈並聯不同的層數對於Q值有何影響。
3.4 測試本次的晶片使用TSMC 0.35um 2P4M的製程製作。
電感測試元件在國家次微米實驗中心使用On-wafer量測。
3.5 討論(a)共振頻率方面：由圖五和圖六都可以明顯看出對稱型電感在差動模式下的確有較高的自振頻率及品質因素。
根據分析，雖然在差動模式下金屬及金屬的雜散電增加，但對地的雜散電容減少更多，所以總的來說整體雜散電容是減少的，所以在差動模式下電感自振頻率較高，也因此電感的品質因素獲得改善。
此外如圖六所示，我們所提出的選取部分金屬並聯電感確實可以改善傳統多層並聯電感(全部金屬並聯電感)自我共振頻率過低的問題。
其次，在我們所應用的範圍中(< 6GHz)，無論是平面電感、傳統多層並聯電感或部分多層並聯電感，其電感值幾乎一樣。
(b)移動f Qmax方面：如圖六所示，量測結果顯示，對稱型電感測試元件可以藉由選取不同金屬並聯使得f Qmax 由3.7GHz移至2.5GHz。
量測結果顯示電感最大Q值頻率由3.7GHz移至2.5GHz，而全部金屬並聯電感最大Q值頻率則落在1.8GHz，量測結果顯示電感最大Q值頻率的確可以藉由選取部份金屬並聯的方式將f Qmax移到電路的工作頻率以改善電路特性。
四、結論本次下線的電感皆完成測試，並且我們也對於電感的結構(並聯層數)對Q值的影響及在不同並聯情況下對Q max值及f Qmax值的變化提出解釋，並亦完成壓控震盪器電路的量測來驗證所提出移動f Qmax值的機制。
五、參考文獻[1] J. Craninckx and M. J. Steyaert, “A 1.8-GHz low-phase-noise CMOS VCO using optimized hollow spiral inductors,” IEEE J. Solid-State Circuits, vol. 32, pp.736-744, May 1997.[2] C. P. Yue and S. S. Wong, “On-chip spiral inductors with patterned ground shields for Si-based RF IC’s,” IEEE J. Solid-State Circuits, vol. 33, pp.743-752, May 1998.[3] J. N. Burghartz, M. Soyuer, and K. A. Jenkins, “Microwave inductors and capacitors in standard multilevel interconnect silicon technology,” IEEE Trans. Microwave Theory and Tech., vol. 44, pp.100-104, Jan. 1996.[4] A. M. Niknejad and R. G. Meye r, “Analysis, design, and optimization of spiral inductors and transformers for Si RF IC’s,” IEEE J. Solid-State Circuits, vol. 33, pp.1470-1481, Oct. 1998.[5] A. Zolfaghari, A. Chan, and B. Razavi, “Stacked Inductors and Transformers in CMOS Technology,” IEEE J. Solid-State Circuits, vol. 36, no. 4, pp. 620-628, Apr. 2001.六、圖表<圖一>平面式電感電壓剖面圖。
Cmm,1Cmm,3<圖二>對稱型電感圖示。
2V 0V 67V 56V 45V 34V 23V 12<圖三>對稱型電感電壓剖面圖。
Q LFrequency<圖四>選取部份金屬並聯電感原理圖示。
Q u a l i t y f a c t o r (Q )Frequency (GHz)<圖五>壓控震盪器電路圖。
Q u a l it y f a c t o r (Q )Frequency (GHz)<圖六>第一組電感測試元件量測結果。
Q d i f fFrequency (GHz)<圖七>第二組電感測試元件量測結果。
<圖七>電感量測圖，使用GSGSG 針。
表一Properties of Different Metal Shunting Configurations in*** Chip Features CAD Tools *** CKT name : Modeling of Symmetric Inductors and Selective Metal Parallel Shunting Technique(設計名稱) HSPICETechnology : 0.35um 2P4M Silicide (使用製程) OPUSPackage : die (包裝種類)Chip Size :1.5 x 1.5 mm2 (晶片面積；mm2)Transistor/Gate Count : 0 (電晶體/邏輯閘數)Power Dissipation : .0mW (功率消耗；mW)Max. Frequency : 10000MHz (最高工作頻率，MHz)Testing Results :■function work □partial work □fail。