自动控制原理及其应用_课后习题答案_第二章
- 格式:pdf
- 大小:4.53 MB
- 文档页数:43

自动控制原理习题及其解答第一章(略) 第二章例2-1 弹簧,阻尼器串并联系统如图2-1示,系统为无质量模型,试建立系统的运动方程。
解:(1) 设输入为y r ,输出为y 0。
弹簧与阻尼器并联平行移动。
(2) 列写原始方程式,由于无质量按受力平衡方程,各处任何时刻,均满足∑=0F ,则对于A 点有021=-+K K f F F F其中,F f 为阻尼摩擦力,F K 1,F K 2为弹性恢复力。
(3) 写中间变量关系式220110)()(y K F Y Y K F dty y d f F K r K r f =-=-⋅=(4) 消中间变量得 020110y K y K y K dtdy f dt dy f r r=-+- (5) 化标准形 r r Ky dtdyT y dt dy T +=+00 其中:215K K T +=为时间常数,单位[秒]。
211K K K K +=为传递函数,无量纲。
例2-2 已知单摆系统的运动如图2-2示。
(1) 写出运动方程式 (2) 求取线性化方程 解:(1)设输入外作用力为零,输出为摆角θ ,摆球质量为m 。
(2)由牛顿定律写原始方程。
h mg dtd l m --=θθsin )(22其中,l 为摆长,l θ 为运动弧长,h 为空气阻力。
(3)写中间变量关系式)(dtd lh θα= 式中,α为空气阻力系数dtd l θ为运动线速度。
(4)消中间变量得运动方程式0s i n 22=++θθθmg dt d al dtd ml (2-1) 此方程为二阶非线性齐次方程。
(5)线性化由前可知,在θ =0的附近,非线性函数sin θ ≈θ ,故代入式(2-1)可得线性化方程为022=++θθθmg dt d al dtd ml 例2-3 已知机械旋转系统如图2-3所示,试列出系统运动方程。
解:(1)设输入量作用力矩M f ,输出为旋转角速度ω 。
(2)列写运动方程式f M f dtd J+-=ωω式中, f ω为阻尼力矩,其大小与转速成正比。

自动控制原理及其应用_课后习题答案_第二章黄坚主编自动化专业课程(2-1a)第二章习题课(2-1a)2-1(a)试建立图所示电路的动态微分方程。
u+ci1=i2-ic+d)+uoR1(ui-uo+u1u[R-CR2u]R1+uoui=dtoi2---C解:CCi1R1R2ic+uoi2-duiduo输入量为ui,输出量为uo。
Rui=u1+uoR2ui=uoR1-CdtR1R2+CdtR12+uoR2ducd(ui-uo)uoic=Cidt=dtu1=i1R1duodui2=RuoR1+CdtR1R2+uoR2=R2ui+CdtR1R22黄坚主编自动化专业课程(2-1b)第二章习题课(2-1b)2-1(b)试建立图所示电路的动态微分方程。
ducCLd2uoduoLduoLic==2+CdtR1uL=dtR2dt+uR2dtd2u+uooCCLoR2duou=+uo+Ci1ii2=Rui=u1+uo2dt-R2R2dt2-输入量为ui,输出量为uo。
u1=i1R1i1=iL+icdiLuL=Ldtducd(ui-uo)ic=Cdt=dtuoiL=i2=R2习题课一(2-2)求下列函数的拉氏变换。
(1)f(t)=in4t+co4tf(t)=in4t+co4tw:L解:∵L[inwt]=22w+L[cowt]=22w+ 4+L∴L[in4t+co4t]=2+162+16+4=2+16黄坚主编自动化专业课程(2)f(t)=t3+e4tf(t)=t3+e4t]=3!+:解:L[t3+1(3)f(t)=tneatf(t)=)=t13!1-4=4+-4:解:L[tneat]=n!(-a)n+1(4)f(t)=(t-1)2e2tf(t)=(t-1)2e2t]=e-(-2)2:解:L[(t-1)(-2)3黄坚主编自动化专业课程2-3-1函数的拉氏变换。
F()=(+1)(+3)F()=+1+1A解:A1=(+2)(+1)(+3)+1A2=(+3)(+1)(+3)1F()=+3-+2F()=2=-3=-1=-2=2f(t)=2e-3t-e-2tf(t)=2e黄坚主编自动化专业课程2-3-2函数的拉氏变换。

第二章习题答案名词解释1.一阶系统:以一阶微分方程作为运动方程的控制系统。
2.二阶系统:能够用二阶微分方程描述的系统。
3.应用函数方框把控制系统的全部变量联系起来以描述信号在系统中流通过程的图示。
4. 应用节点、支路把控制系统的全部变量联系起来以描述信号在系统中流通过程的图示。
5.初始条件为零时,线性定常系统或元件输出信号的拉氏变换与输入信号的拉氏变换的比。
6.从源点到阱点的通路上,通过任何节点不多于一次,称为前向通路。
7. 既有输入支路又有输出支路的节点。
8.动态模型:描述变量各阶导数之间关系的微分方程。
9.静态数学模型:在静态条件下(即变量各阶导数为零),描述变量之间关系的代数方程 。
简答1.能够提高的稳定裕度,抑制超调,但对噪声信号具有较高的增益。
2.比例微分(PD )控制和测速(微分)反馈。
3.a.系统是线性定常;b.零初始条件。
4.时域中常用的数学模型有微分方程、差分方程、和状态方程;复数域中有传递函数、结构图;频域中有频率特性等。
计算题1.解:通过比较点前移串倒数,引出点后移串倒数得31313322113211)()(H H G G H G H G H G G G G s R s C ++++=2.解:利用复阻抗的概念)(1/1/1)(2s U CsR Ls Cs s U ++= 则,传递函数为11)(1)(22++=RCs LCs s U s U 3.解:2条前向通道:4123211G G P G G G P == 5个回路: 415244232332121211G G L H G L H G G L G G -G L -=-=-==-=H G G L不存在不接触回路。
故,有:GG H G H G G G G G H G G L L L L L 124232321121543211)(1+++++=++++-=∆5个回路均与2个前向通道相接触,于是: 1 121=∆=∆ ()41242323211214132122111G G G G G P P 1P R(S)C(S)G G H G H G G G G G H G G ++++++=∆+∆∆== 4. 解:输入的拉氏变换:s s R /1)(= 输出的拉氏变换:11211)(+++-=s s s s C 则传递函数为: 22111)()()(+++-==s s s R s C s G 5.解:利用复阻抗的概念,有:)(1//)(212s U R CsR R s U r c += 所以,2212)1()1(11//)()(112122112212++=+++=++=+=s s R Cs R R Cs R R R Cs R R R R Cs R R s U s U r c 6 解:利用复阻抗的概念,有:)(1//)(212s U R CsR R s U r c += 所以,21)1()1(11//)()(112122112212++=+++=++=+=s s R Cs R R Cs R R R Cs R R R R Cs R R s U s U r c 7. 解:将G 3(S) 和G 4(S)两方框之间的引出点后移得:传递函数1432134323243211)()(H G G G G H G G H G G G G G G s R s C +++= 8. 解:对方程求拉氏变换,即得传递函数: 25.10125.0)(+=s s G。

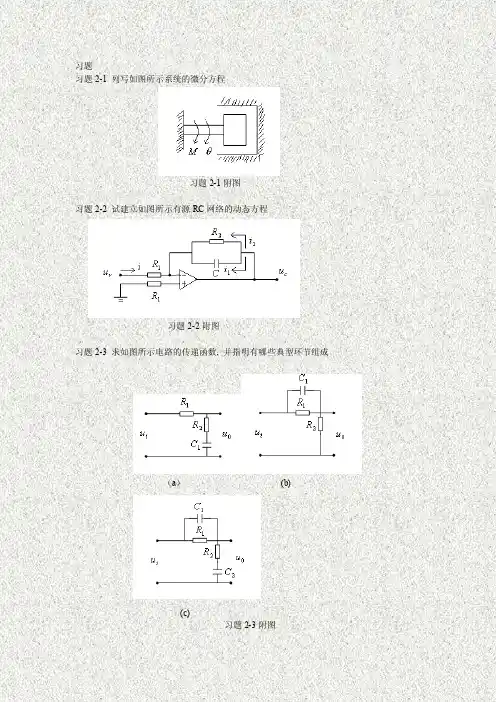
习题习题2-1 列写如图所示系统的微分方程习题2-1附图习题2-2 试建立如图所示有源RC网络的动态方程习题2-2附图习题2-3 求如图所示电路的传递函数, 并指明有哪些典型环节组成(a)(b)(c)习题2-3附图习题2-4 简化如图所示方块图, 并求出系统传递函数习题2-4附图习题2-5 绘制如下方块图的等效信号流图, 并求传递函数图(a)图(b)习题2-5附图习题2-6 系统微分方程组如下, 试建立对应信号流图, 并求传递函数。
),(d )(d )(),(d )(d ),()()()(),()(),(d )(d )(),()()(54435553422311121t y tt y T t x k t x k tt x t y k t x t x t x t x k t x t x k tt x t x t y t r t x +==--==+=-=τ习题2-7 利用梅逊公式直接求传递函数。
习题2-7附图习题2-8 求如图所示闭环传递函数, 并求(b)中)(s H x 的表达式, 使其与(a)等效。
图(a )图(b)习题2-8附图习题2-9 求如下各图的传递函数(a)(b)(c)习题2-9附图习题2-10 已知某些系统信号流图如图所示, 求对应方块图(a )(b)(c)(d)习题2-10附图习题答案习题2-1答案:解:设外加转矩M 为输入量,转角θ为输出量,转动惯量J 代表惯性负载,根据牛顿定律可得:θθθ1122d d d d k t f M tJ --=式中,1,1,k f 分别为粘性阻尼系数和扭转弹性系数,整理得:M k t f tJ =++θθθ1122d d d d习题2-2答案:解: 设r u 为输入量,c u 为输出量,,,,21i i i 为中间变量,根据运算放大器原理可得:1221d d R u i R u i t u c i r c c ===消去中间变量可得: r c c u R Ru t u C R 122d d -=+ 习题2-3答案: 解: (a)11111111221212211121121120++=+++=+++=+++=Ts Ts s R R R C R s C R R sC R sC R sC sC R R sC R u u i β其中:221121,R R R C R T +==β, 一阶微分环节,惯性环节.(b)21121212111221122011//1R R s C R R R s C R R R sC R R R sC R R u u i+++=++=+= 11111111212121221121111++=+∙++∙+=+++=Ts Ts s C R R R R s C R R R R R R s C R R s C R αα其中 α=+=21211,R R R T C R , 一阶微分环节,惯性环节.(c)s C R s C R s C R s C R s C R sC R R sC sC R u u i 21221122112211220)1)(1()1)(1(1//11+++++=+++= 由微分环节,二阶振荡环节组成。
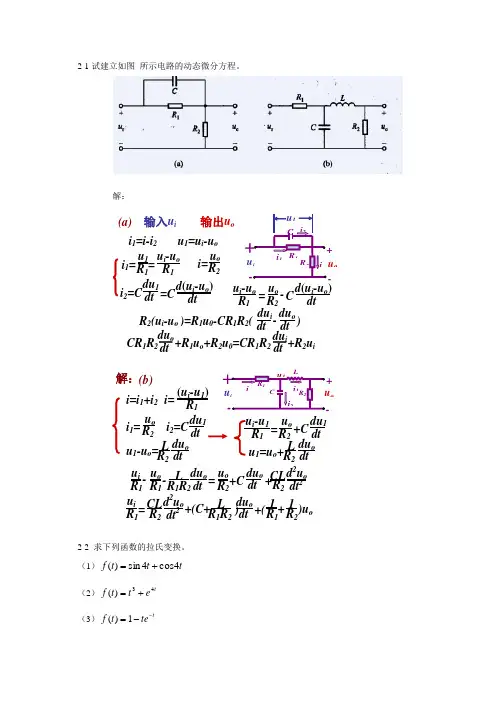
2-1试建立如图 所示电路的动态微分方程。
解:输入u i 输出u ou 1=u i -u oi 2=C du 1 dt )- R 2(u i -u o )=R 1u 0-CR 1R 2( du i dt dt du oC + - u i o R 1R 2 i 1 i i 2u 1i 1=i-i 2 u o i= R 2u 1 i 1= R 1 = u i -u o R 1 dt d (u i -u o ) =C C d (u i -u o ) dtu o - R 2 = u i -u o R 1 CR 1R 2 du o dt du idt +R 1u o +R 2u 0=CR 1R 2 +R 2u i(a)i=i 1+i 2 i 2=C du 1 dtu o i 1= R 2 u 1-u o = L R 2 du o dt R1i= (u i -u 1) (b)C+-iu o R 1R 2i 1 ii 2Lu 1 = R 1 u i -u 1 u o +C R 2 du 1 dtu 1=u o + L R 2 du o dtdu o dt R 1R 2 L du o dt + CL R 2 d 2u o dt 2 = - - u i R 1 u o R 1 u o R 2 +C )u o R 1R 2 L du o dt ) CL R 2 d 2u o dt 2 = + +( u i R 1 1 R 11 R 2+(C+ 解:2-2 求下列函数的拉氏变换。
(1)t t t f 4cos 4sin )(+= (2)te t tf 43)(+= (3)t te t f --=1)((4)te t tf 22)1()(-= 解:(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s s+42+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解:(2) f(t)=t 3+e 4t 解:L [t 3+e 4t ]= 3!s 41s-4+ 6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解:解:2-3求下列函数的拉氏反变换。
![自动控制原理及其应用_课后习题答案_2[1]](https://uimg.taocdn.com/5164ec0ff78a6529647d53a6.webp)


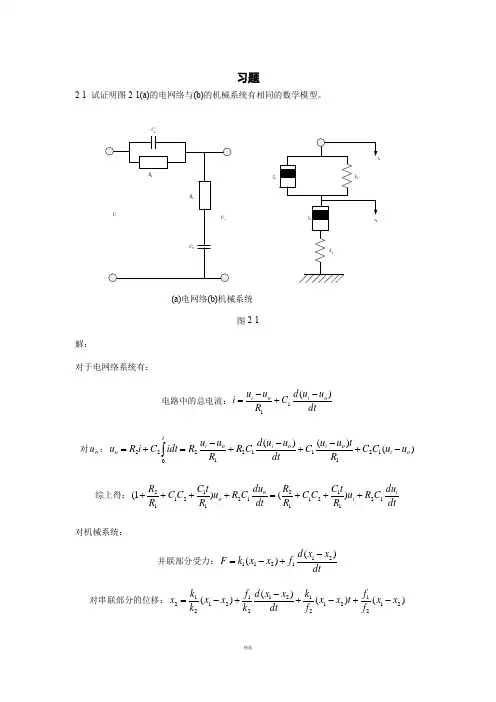
习题2-1 试证明图2-1(a)的电网络与(b)的机械系统有相同的数学模型。
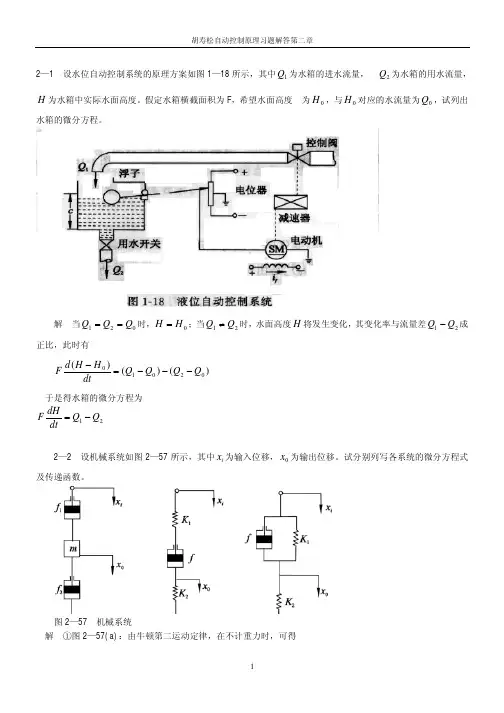
1C 1f 1(a)电网络(b)机械系统图2-1解:对于电网络系统有:电路中的总电流:dtu u d C R u u i o i o i )(11-+-=对o u :)()()(1211121222o i o i o i o i to u u C C R t u u C dt u u d C R R u u R idt C i R u -+-+-+-=+=⎰综上得:dtdu C R u R tC C C R R dt du C R u R t C C C R R i i o o 1211211212112112)()1(+++=++++对机械系统:并联部分受力:dtx x d f x x k F )()(211211-+-= 对串联部分的位移:)()()()(21212121212121212x x f f t x x f k dt x x d k f x x k k x -+-+-+-=整理得:dtdx k f x f f t f k k k dt dx k f x f f t f k k k 12122121212211212121)()1(+++=++++所以,两系统具有相同的数学模型2-5求图2-2中RC 电路和运算放大器的传递函数c ()/()i U s U s 。
1R1R(a) RC 电路 (b) RC 电路1R(c) RC 电路 (d) 运算放大器图2-2解:21212)()()R sCR R R R s u s u a r c ++=οο1)()()()()()()3122112322121121211231212112++++++++=S R C R C R C S R R C C R R C C SR C R C S R R C C R R C C s u s u b rc οο2121212)()()()R R S CR CR R R CS R s u s u c r c +++=οο21212112)()()()S LCR R R S CR R LR R LS s u s u d r c ++++=οο2-6求图2-3所示系统的传递函数C(s)/D(s)和E(s)/D(s)。
自动控制原理第二章课后习题答案(免费)离散系统作业注明:*为选做题2-1 试求下列函数的Z 变换 (1)()E z L =();n e t a = 解:01()[()]1k k k z E z L e t a z z z aa∞-=====--∑ (2) ();at e t e -= 解:12211()[()][]1...1atakT k aT aT aTaT k z E z L e t L ee z e z e z z e e z∞----------=====+++==--∑2-2 试求下列函数的终值:(1)112();(1)Tz E z z --=-解: 11111()(1)()1lim lim lim t z z Tz f t z E z z---→∞→→=-==∞- (2)2()(0.8)(0.1)z E z z z =--。
解:211(1)()(1)()0(0.8)(0.1)lim lim limt z z z z f t z E z z z →∞→→-=-==-- 2-3* 已知()(())E z L e t =,试证明下列关系成立:(1)[()][];n z L a e t E a =证明:0()()nn E z e nT z∞-==∑00()()()()[()]n n n n n n z z E e nT e nT a z L a e t a a ∞∞--=====∑∑ (2)()[()];dE z L te t TzT dz=-为采样周期。
证明:11100[()]()()()()()()()()()nn n n n n n n n n L te t nT e nT zTz ne nT z dE z de nT z dz dz e nT n zne nT z ∞∞---==∞-=∞∞----======-=-∑∑∑∑∑所以:()[()]dE z L te t Tzdz=- 2-4 试求下图闭环离散系统的脉冲传递函数()z Φ或输出z 变换()C z 。
第二章2-3试证明图2-5( a )的电网络与(b)的机械系统有相同的数学模型。
分析首先需要对两个不同的系统分别求解各自的微分表达式,然后两者进行对比,找岀两者之间系数的对应关系。
对于电网络,在求微分方程时,关键就是将元件利用复阻抗表示,然后利用电压、电阻和电流之间的关系推导系统的传递函数,然后变换成微分方程的形式,对于机械系统,关键就是系统的力学分析,然后利用牛顿定律列岀系统的方程,最后联立求微分方程。
证明:(a)根据复阻抗概念可得:即取A、B两点进行受力分析,可得:整理可得:经比较可以看岀,电网络( a)和机械系统(b)两者参数的相似关系为2-5 设初始条件均为零,试用拉氏变换法求解下列微分方程式,并概略绘制x(t)曲线,指岀各方程式的模态。
(1)(2 )2-7由运算放大器组成的控制系统模拟电路如图2-6所示,试求闭环传递函数U c ( s )/Ur ( s)。
图2-6 控制系统模拟电路解:由图可得联立上式消去中间变量U1和U2,可得:2-8某位置随动系统原理方块图如图2-7所示。
已知电位器最大工作角度,功率放大级放大系数为K3,要求:(1) 分别求岀电位器传递系数K 0、第一级和第二级放大器的比例系数 K 1和K 2;(2) 画岀系统结构图; (3) 简化结构图,求系统传递函数。
图2-7 位置随动系统原理图(2)假设电动机时间常数为 Tm 忽略电枢电感的影响,可得直流电动机的传递函数为 式中Km 为电动机的传递系数,单位为。
又设测速发电机的斜率为,则其传递函数为由此可画岀系统的结构图如下:(3)简化后可得系统的传递函数为2-9若某系统在阶跃输入 r(t)=1(t) 时,零初始条件下的输岀 响应,试求系统的传递函数 和脉冲响应。
分析:利用拉普拉斯变换将输入和输出的时间域表示变成频域表示,进而求解出系统的传递函数,然后对传递函数进行反变换求岀系统的脉冲响应函数。
解:(1),则系统的传递函数 (2)系统的脉冲响应2-10试简化图2-9中的系统结构图,并求传递函数 C(s)/R(s ) 和C(s)/N(s) 分析:分别假定R(s)=o 和N(s)=O ,画出各自的结构图,然后对系统结构图进行等效变换, 将其化成最简单的形式,从而求解系统的传递函数。
自动控制原理第二章到第七章课后习题答案第二章2-1试求下图所示电路的微分方程和传递函数。
解:(a )根据电路定律,列写出方程组:001Li R c L R C di L u u dtu R i i dt Ci i i ⋅+==⋅==+⎰消除中间变量可得微分方程:20002i d u du L L C u u dt R dt⋅⋅+⋅+=对上式两边取拉氏变换得:2000()()()()i LL C U s s U s s U s U s R⋅⋅⋅+⋅⋅+= 传递函数为022()1()()1i U s R G s L U s R Ls LCRs s LCs R ===++++ (b )根据电路定律,列写出方程组:12011()i i u i R R idt C u u i R =++-=⎰消除中间变量可得微分方程:121012i R R Ru u idt R R C+=-⎰ 对上式两边取拉氏变换得:2012()(1)()(1)i U s R Cs U s R Cs R Cs +=++传递函数为0212()1()()1i U s R CsG s U s R Cs R Cs+==++2-3求下图所示运算放大器构成的电路的传递函数。
解:(a )由图(a ),利用等效复数阻抗的方法得22111(s)1(s)()1o i R U R Cs Cs G U s R R Cs ++==-=-+(b )由图(b ),利用等效复数阻抗的方法得222121211221211111(s)()1(s)1()1o i R U C s R R C C s R C R C s G U s R C s R C s R C s++++==-=-+2-5试简化下图中各系统结构图,并求传递函数()()C s R s 。
2-6试求下图所示系统的传递函数11()()C s R s ,21()()C s R s ,12()()C s R s 及22()()C s R s 。