大欧拉角的空间直角坐标转换方法探讨

直角坐标系中的几何变换方法总结直角坐标系是我们在数学和物理学中经常使用的一种坐标系统。

在直角坐标系中，我们可以通过坐标点的位置来描述一个点的位置。

然而，在实际问题中，我们经常需要对坐标系进行一些变换，以便更好地解决问题。

本文将总结一些常见的几何变换方法，帮助读者更好地理解和应用直角坐标系。

一、平移变换平移变换是指在直角坐标系中将一个图形沿着某个方向移动一定的距离。

平移变换不改变图形的形状和大小，只改变了它的位置。

在直角坐标系中，我们可以通过将图形中的每个点的坐标增加或减少相同的数值来实现平移变换。

例如，如果我们要将一个图形沿着x轴正方向平移3个单位，我们可以将每个点的x坐标加3。

二、旋转变换旋转变换是指在直角坐标系中将一个图形绕着某个点或某个轴旋转一定的角度。

旋转变换不改变图形的大小和形状，只改变了它的方向。

在直角坐标系中，我们可以通过将图形中的每个点绕着旋转中心进行旋转来实现旋转变换。

旋转的角度可以用弧度或度数来表示。

例如，如果我们要将一个图形绕着原点逆时针旋转90度，我们可以使用旋转矩阵来计算每个点的新坐标。

三、缩放变换缩放变换是指在直角坐标系中将一个图形沿着某个方向放大或缩小一定的比例。

缩放变换改变了图形的大小，但不改变它的形状和方向。

在直角坐标系中，我们可以通过将图形中的每个点的坐标乘以相同的比例因子来实现缩放变换。

例如，如果我们要将一个图形沿着x轴方向放大2倍，我们可以将每个点的x坐标乘以2。

四、对称变换对称变换是指在直角坐标系中将一个图形关于某个点、某个直线或某个平面进行对称。

对称变换不改变图形的大小和形状，只改变了它的位置。

在直角坐标系中，我们可以通过将图形中的每个点的坐标关于对称中心进行对称来实现对称变换。

例如，如果我们要将一个图形关于x轴进行对称，我们可以将每个点的y坐标取负值。

五、剪切变换剪切变换是指在直角坐标系中将一个图形沿着某个方向进行拉伸或压缩。

剪切变换改变了图形的形状，但不改变它的大小和方向。

欧拉角与旋转矩阵的转换方法欧拉角（Euler angles）和旋转矩阵（rotation matrix）是描述物体在三维空间中旋转的常用数学工具。

欧拉角由三个旋转轴和三个旋转角度组成，而旋转矩阵是一个3x3的正交矩阵。

这两种表示方法之间的转换方法可以分为两个步骤：将欧拉角转换为旋转矩阵，或将旋转矩阵转换为欧拉角。

一、欧拉角转换为旋转矩阵欧拉角的转换公式有多种实现方式，其中最为常用的是Z-Y-X欧拉角序列的转换公式。

假设欧拉角序列为ψ、θ、φ（分别表示绕Z轴、Y轴和X轴的旋转角度），则对应的旋转矩阵R可以通过以下的步骤来计算：1.将ψ、θ、φ分别转换为对应的旋转矩阵Rz(ψ)、Ry(θ)和Rx(φ)，这里Rz、Ry和Rx分别表示绕Z轴、Y轴和X轴的旋转矩阵。

2.将Rz(ψ)、Ry(θ)和Rx(φ)按照Z-Y-X的次序相乘，得到最终的旋转矩阵R=Rz(ψ)Ry(θ)Rx(φ)。

具体地，Rz(ψ)、Ry(θ)和Rx(φ)的计算公式如下：Rz(ψ) = [[cos(ψ), -sin(ψ), 0], [sin(ψ), cos(ψ), 0], [0, 0, 1]]Ry(θ) = [[cos(θ), 0, sin(θ)], [0, 1, 0], [-sin(θ), 0, cos(θ)]]Rx(φ) = [[1, 0, 0], [0, cos(φ), -sin(φ)], [0, sin(φ), cos(φ)]]将以上的计算公式代入到步骤2中，就可以得到欧拉角对应的旋转矩阵R。

二、旋转矩阵转换为欧拉角将旋转矩阵转换为欧拉角的过程比较复杂，通常需要分解出旋转矩阵的三个旋转角度。

下面介绍一种常用的分解方法，即将旋转矩阵分解为绕Z轴、Y轴和X轴旋转的角度。

假设旋转矩阵为R，则分解的步骤如下：1.计算R矩阵第三列的单位向量v32. 计算v3在xz平面上的投影v3_projected，即将v3的y分量设为0。

3. 计算v3与单位向量z的夹角θ1、可以使用反余弦函数计算cos(θ1) = v3_projected · z，其中·表示向量的点积。

旋转矩阵、欧拉⾓、四元数理论及其转换关系1. 概述旋转矩阵、欧拉⾓、四元数主要⽤于表⽰坐标系中的旋转关系，它们之间的转换关系可以减⼩⼀些算法的复杂度。

本⽂主要介绍了旋转矩阵、欧拉⾓、四元数的基本理论及其之间的转换关系。

2、原理2.1 旋转矩阵对于两个三维点p1(x1,y1,z1)，p2(x2,y2,z2)，由点 p1 经过旋转矩阵 R 旋转到 p2，则有注：旋转矩阵为正交矩阵RR^T=E任意旋转矩阵：任何⼀个旋转可以表⽰为依次绕着三个旋转轴旋三个⾓度的组合。

这三个⾓度称为欧拉⾓。

三个轴可以指固定的世界坐标系轴，也可以指被旋转的物体坐标系的轴。

三个旋转轴次序不同，会导致结果不同。

2.2 欧拉⾓欧拉⾓有两种：静态：即绕世界坐标系三个轴的旋转，由于物体旋转过程中坐标轴保持静⽌，所以称为静态。

动态：即绕物体坐标系三个轴的旋转，由于物体旋转过程中坐标轴随着物体做相同的转动，所以称为动态。

使⽤动态欧拉⾓会出现万向锁现象；静态欧拉⾓不存在万向锁的问题。

对于在三维空间⾥的⼀个参考系，任何坐标系的取向，都可以⽤三个欧拉⾓来表现。

参考系⼜称为实验室参考系，是静⽌不动的。

⽽坐标系则固定于刚体，随着刚体的旋转⽽旋转。

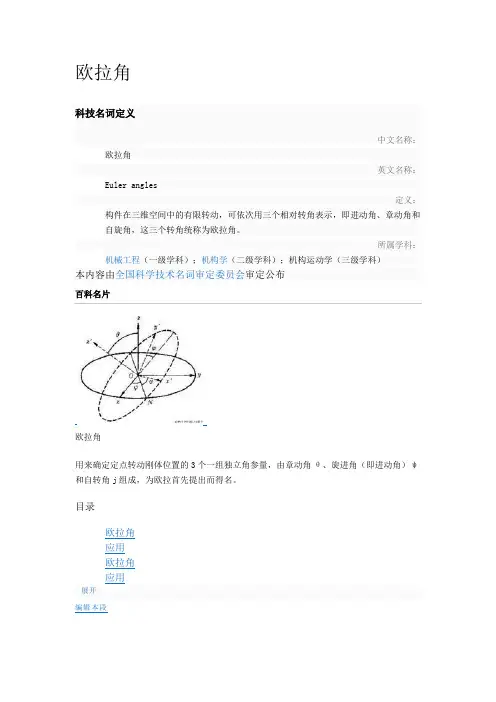
如图1，设定xyz-轴为参考系的参考轴。

称xy-平⾯与XY-平⾯的相交为交点线，⽤英⽂字母（N）代表。

zxz顺规的欧拉⾓可以静态地这样定义：α是x-轴与交点线的夹⾓，β是z-轴与Z-轴的夹⾓，γ是交点线与X-轴的夹⾓。

图中三个欧拉⾓分别为：(α,β,γ)；蓝⾊的轴为：xyz轴红⾊的轴为：XYZ轴绿⾊的线为交线：Nα∈[0,2π],β∈[0,π],γ∈[0,2π]很可惜地，对于夹⾓的顺序和标记，夹⾓的两个轴的指定，并没有任何常规。

科学家对此从未达成共识。

每当⽤到欧拉⾓时，我们必须明确的表⽰出夹⾓的顺序，指定其参考轴。

实际上，有许多⽅法可以设定两个坐标系的相对取向。

欧拉⾓⽅法只是其中的⼀种。

此外，不同的作者会⽤不同组合的欧拉⾓来描述，或⽤不同的名字表⽰同样的欧拉⾓。

欧拉角科技名词定义中文名称：欧拉角英文名称：Euler angles定义：构件在三维空间中的有限转动，可依次用三个相对转角表示，即进动角、章动角和自旋角，这三个转角统称为欧拉角。

所属学科：机械工程（一级学科）；机构学（二级学科）；机构运动学（三级学科）本内容由全国科学技术名词审定委员会审定公布欧拉角用来确定定点转动刚体位置的3个一组独立角参量，由章动角θ、旋进角（即进动角）ψ和自转角j组成，为欧拉首先提出而得名。

目录它们有多种取法，下面是常见的一种。

如图所示，由定点O作出固定坐标系Oxyz和固连于刚体的动坐标系Ox′y′z′。

以轴Oz和Oz′为基本轴，其垂直面Oxy和Ox′y′为基本平面。

由轴Oz欧拉角量到Oz′的角θ称章动角。

平面zOz′的垂线ON称节线，它又是基本平面Ox′y′和Oxy的交线。

在右手坐标系中，由ON的正端看，角θ应按逆时针方向计量。

由固定轴Ox量到节线ON的角ψ称旋进角；由节线ON量到动轴Ox′的角j称自转角。

由轴Oz和Oz′正端看，角ψ和j也都按逆时针方向计量。

若令Ox′y′z′的初始位置与Oxyz重合，经过相继绕Oz、ON和Oz′的三次转动后，刚体将转到图示的任意位置。

如果刚体绕通过定点O的某一轴线以角速度ω转动，而ω在动坐标系Ox′y′z′上的投影为ωx′、ωy′、ωz′，则它们可用欧拉角及其微商表示如下：ωx′＝sinθsinj＋cosj，ωy′＝ sinθcosj－sinj，ωz′＝cosθ＋。

如果已知ψ、θ、j和时间的关系，则可用上式计算ω在动坐标轴上的3个分量；反之，如已知任一瞬时t的ω各个分量，也可利用上式求出ψ、θ、j和时间t的关系，因而也就决定了刚体的运动。

上式通常被称为欧拉运动学方程。

原理欧拉角Eulerian angles用来唯一地确定定点转动刚体位置的三个一组独立角参量[1]，由章动角θ、进动角ψ和自转角嗞组成，为L.欧拉首先提出，故得名。

对于任何一个参考系，一个刚体的取向，是依照顺序，从这参考系，做三个欧拉角的旋转而设定的。

§不同坐标系之间的变换欧勒角与旋转矩阵X 对于二维直角坐标, 如图所示， 有: X2 y2 cos sinsi n cos在三维空间直角坐标系中, 两坐标系间的变换一般需要在三个坐标平面上, 图所示，设旋转次序为: ①绕OZ1旋转Z 角，OX 1,OY 1旋 转至OX 0,OY0； ②绕0丫0旋转丫角OX 0,OZ 1旋转至 OX 2,OZ 0； ③绕OX 2旋转X 角，O 丫0,OZ旋转至 OY 2, OZ 2。

X 1 y1(10-8) 具有相同原点的 通过三次旋转才能完成。

如 SxarZj rX ,丫，Z 为三维空间直角坐标变换的三个旋转角，也称欧勒角，与它 10 0&( X )0 cos XsinsinXcoscos Y 0 sin R 2( Y )0 1 0sin Y 0cos Y相对应的旋转矩阵分别为: YX (10-10) X (10-11)R3(Z) cos Z sin Z0sin Z cos Z00 0 1(10-12)令R o R1 ( X )R2 ( Y )R3( Z (10-13) 则有:X2丫2 J R1 ( X )R2 ( Y )R3(X1z) Y1Z1R oX1丫1Z1(10-14)代入:cos Y cos ZR o cos X sin z sin X si门丫cosZsin X sin Z cos X sin Y cosZcos Y sin Zcos X cos Z sin X si门丫sin Zsin X cos Z cos X sin Y sinZ为微小转角, 可取:于是可化简R o X(10-16)1上式称微分旋转矩阵。

不同空间直角坐标之间的变换当两个空间直角坐标系的坐标换算既有旋转又有平移时，则存在三个平移参数和三个旋转参数，再顾及两个坐标系尺度不尽一致，从而还有一sin Y sin X cos Y COS X COS Y个尺度变化参数，共计有七个参数。

世界坐标系到相机坐标系变换矩阵及欧拉角计算一、概述在计算机视觉和计算机图形学领域中，世界坐标系到相机坐标系变换矩阵和欧拉角计算是非常重要且常用的技术。

本文将通过具体的介绍和示例，详细讨论世界坐标系到相机坐标系变换矩阵及欧拉角的计算方法。

二、世界坐标系和相机坐标系简介1. 世界坐标系世界坐标系是指在三维空间中描述物体位置和方向的坐标系。

它通常是一个固定的参考框架，用于描述物体在空间中的位置和姿态。

2. 相机坐标系相机坐标系是相机传感器坐标系中的一个坐标系，它描述了相机的位置和方向。

相机坐标系通常位于相机传感器中心，其坐标轴与传感器平面平行。

三、世界坐标系到相机坐标系变换矩阵的推导1. 坐标变换原理当世界坐标系中的物体经过相机的观测时，需要将物体的坐标转换到相机坐标系中。

这个转换过程可以通过一个变换矩阵来实现，该矩阵包括平移、旋转和缩放等变换操作。

2. 变换矩阵的计算设世界坐标系下的一个物体点坐标为Pw = (Xw, Yw, Zw)，相机坐标系下的坐标为Pc = (Xc, Yc, Zc)。

那么Pc与Pw之间的变换关系可以表示为：Pc = T * R * Pw其中T为平移矩阵，R为旋转矩阵。

根据相机的内参矩阵和外参矩阵，可以得到T和R的具体数值，进而得到世界坐标系到相机坐标系的变换矩阵。

四、欧拉角的计算方法1. 欧拉角的定义欧拉角是描述物体姿态的一种方式，它由三个角度组成，通常分别表示绕三个坐标轴的旋转角度。

2. 欧拉角的计算在计算机视觉中，通常使用旋转矩阵或四元数来表示物体的旋转姿态。

而将旋转矩阵或四元数转换为欧拉角则是一个常见的需求。

欧拉角的计算方法有多种，常见的包括将旋转矩阵转换为欧拉角、将四元数转换为欧拉角等。

五、示例分析以下将通过一个具体的示例来演示世界坐标系到相机坐标系的变换矩阵和欧拉角的计算方法。

假设世界坐标系中的一个物体点坐标为Pw = (1, 1, 1)，相机坐标系的内参矩阵为K，外参矩阵为[R|T]。

⼤学物理学理论⼒学—欧拉⾓对于欧拉⾓的认识[摘要]基于欧拉⾓的学习，加深认识关于欧拉⾓的相关知识点。

定点运动的刚休可由欧拉⾓来描写出发，通过计算刚体上任意⼀点的速度来引⼊刚体的⾓速度。

从欧拉⾓的理解中做到熟练掌握欧拉⾓、欧拉⾓的矩阵形式的表⽰、明确欧勒⾓的含义和它为什么完整的描述了定点转动刚体的运动状态，以及欧拉⾓在刚体⼒学中的具体应⽤，从⽽更好的理解欧拉⾓。

[关键词]欧拉⾓的定义；⾓速度；⾓加速度；刚体定点转动的应⽤ 1：欧拉⾓的定义虽然当刚体作定点转动时，我们可选这个定点作为坐标系的原点，⽽⽤三个独⽴的⾓度来确定转动轴在空间的取向和刚体绕该轴线所转过的⾓度。

刚体转动可以表⽰为空间坐标系到本体坐标系的⼀个正交变换，变换矩阵由9个⽅向余弦决定，但它们中只有3个是独⽴的，使⽤起来不⽅便。

最好能⽤有明确⼏何意义的3个变量来描述刚体的位置，前⾯已证明，可以给出刚体上的⼀个轴的⽅向，和刚体绕这个轴的转⾓来描述刚体定点运动的位置，因此我们可以⽤类似球坐标中的极⾓θ和⽅位⾓φ来给出轴的取向，再加上绕这个轴旋转的⾓度φ，三个⾓度来描述刚体的定点转动，它们合称为欧拉⾓我们要把本体坐标系和空间坐标系间的正交变换⽤欧拉⾓表⽰出来。

如上图所⽰，向由θ和φ决定，⽽φ是刚体绕该轴的转⾓。

从坐标变换的⾓度看，本体坐标转到图(c)的状态，可以分解为从图(a)经过(b)，通过相继三次2D 旋转得到的(假定开始时本体坐标系x x y z '''-与空间坐标系o xyz -重合)：⑴o xyz o εηζ-→-本体坐标系绕z 轴在xy 平⾯上旋φ⾓：cos sin 0sin cos 0001x y z εφφηφφζ?????? ?=- ? ??? ? ??????⑵o εηζεηζ'''-→，本体坐标系绕ε轴在ηζ平⾯转过θ⾓：1000cos sin 0sin cos εεηθθηζθθζ'?????? ? ???'= ? ??? ? ???'-??????⑶x y z εηζ''''''→本体坐标绕ζ'轴在ηε''平⾯(阴影)转过ψ⾓：cos sin 0sin cos 0001x y z ψψψψ'???? ?'=- '变换矩阵就是三个2D 变换矩阵之积：cos sin 0100cos sin 0sin cos 00cos sin sin cos 00010sin cos 001x x ψψφφψψθθφφθθ?????? ?????'=-- ????? ?????-??????它们由3个欧拉⾓决定。

[转]欧拉⾓与旋转1，什么是欧拉⾓欧拉⾓的基本思想是将⾓位移分解为绕三个互相垂直轴的三个旋转组成的序列。

这听起来复杂，其实它是⾮常直观的。

之所以有“⾓位移”的说法正是因为欧拉⾓能⽤来描述任意旋转，但最有意义的是使⽤笛卡尔坐标系并按照⼀定顺序所组成的旋转序列。

最常⽤的约定，即所谓“heading-pitch-bank”约定。

在这个系统中，⼀个⽅位被定义为⼀个heading⾓，⼀个pitch⾓，和⼀个bank⾓。

它的基本思想就是让物体开始于“标准”⽅位——就是物体坐标轴和惯性坐标轴对齐。

在标准⽅位上，让物体作heading,pitch,bank旋转，最后物体到达我们想要描述的⽅位。

在精确定义术语“heading”“pitch”“bank”前，先让我们简要回顾本书中使⽤的坐标空间约定。

我们使⽤左⼿坐标系，+x向右，+y向上，+z向前。

heading为绕y轴的旋转量，向右旋转为正，旋转正⽅向是顺时针⽅向，经过heading旋转之后，pitch为绕x轴的旋转量，注意是物体坐标系的x轴，不是原惯性坐标系的x轴，依然遵守左⼿法则，向下旋转为正。

最后，经过了heading,pitch后，bank为绕z轴的旋转量，依然是物体坐标系的z轴。

当我们说到旋转的顺序是heading-pitch-bank时，是指从惯性坐标系到物体坐标系，如果从物体坐标系到惯性坐标系则相反。

2，关于欧拉⾓的其他约定前⾯曾提到过，heading-pitch-bank系统不是惟⼀的欧拉⾓系统，绕任意三个互相垂直轴的任意旋转序列都能定义⼀个⽅位。

所以，多种选择导致了欧拉⾓约定的多样性：1）heading-pitch-bank系统有两个名称，当然，不同的名字并不代表不同的约定，这其实并不重要，⼀组常⽤的术语是roll-pitch-yaw，其中的roll对应与bank，yaw对应于heading，它定义了从物体坐标系到惯性坐标系的旋转顺序2）任意三个轴都能作为旋转轴，不⼀定必须是笛卡尔轴，但是⽤笛卡尔轴最有意义3）也可以选⽤右⼿坐标规则4）旋转可以以不同的顺序进⾏3，优点：1）容易使⽤；2）表达简洁；3）任意三个⾓都是合法的4，缺点：1）给定⽅位的表达⽅式不唯⼀；2）两个⾓度间求插值⾮常困难采⽤限制欧拉⾓的⽅法来避免以上问题的出现：heading限制在+-180，pitch为+-90。

空间坐标变换空间坐标变换是指将一个坐标系下的点在另一个坐标系下进行表示的过程。

它在许多领域中都有广泛的应用，例如计算机图形学、机器人技术、地理信息系统等。

在这篇文章中，我们将介绍空间坐标变换的基本概念和常见的变换方法。

一、空间坐标系空间坐标系是一个用于描述三维空间中点的系统。

常见的坐标系有直角坐标系、极坐标系和球坐标系等。

在直角坐标系中，一个点的位置可以由其在三个相互垂直的轴上的坐标表示。

例如，一个点的直角坐标为（x，y，z），其中x、y、z分别表示其在x轴、y轴和z轴上的坐标值。

二、空间坐标变换的基本概念空间坐标变换是指将一个坐标系下的点在另一个坐标系下进行表示的过程。

在进行坐标变换时，我们通常需要考虑平移、旋转和缩放等操作。

以下是空间坐标变换中常用的几种基本操作：1. 平移：平移是指将点沿着某个方向移动一定的距离。

平移操作可以通过在原始坐标上加上平移向量来实现。

2. 旋转：旋转是指将坐标系绕某个轴进行旋转。

旋转操作可以通过矩阵乘法或四元数运算来表示。

3. 缩放：缩放是指将坐标系在各个轴上进行拉伸或压缩。

缩放操作可以通过矩阵乘法来实现。

三、空间坐标变换的常见方法1. 矩阵变换法：矩阵变换法是一种常见的空间坐标变换方法。

它通过矩阵的乘法来表示平移、旋转和缩放等操作。

假设我们有一个点P在坐标系A下的坐标为（x，y，z），要将其转换到坐标系B下，可以使用以下矩阵方程表示：[x'] [a b c d] [x][y'] = [e f g h] * [y][z'] [i j k l] [z][1 ] [0 0 0 1] [1]其中，（x'，y'，z'）表示点P在坐标系B下的坐标。

矩阵中的（a，b，c）表示坐标系B相对于坐标系A的x轴方向的变换，（d，e，f）表示y轴方向的变换，（g，h，i）表示z轴方向的变换。

2. 四元数变换法：四元数变换法是一种常用的空间坐标变换方法。

欧拉角与密勒指数的转换欧拉角和密勒指数的概述欧拉角的定义和意义欧拉角是一种用于描述物体在空间中旋转的方法，它由3个连续旋转组成，分别绕X轴、Y轴和Z轴旋转。

欧拉角的三个分量通常用α、β和γ来表示，分别代表绕X、Y和Z轴旋转的角度。

欧拉角具有很好的几何直观性，可以直观地表示物体在空间中的方向和姿态。

它在航空、航天、机器人、计算机图形学等领域被广泛应用。

密勒指数的定义和意义密勒指数是描述晶体中晶面方向的方法之一，它由一组整数表示，用来表示晶体中的晶面在晶体学坐标系中的方向。

密勒指数的每个整数代表了晶面与坐标轴的交点所位于的位置。

密勒指数可以有效地表示晶体的晶面方向，对于研究晶体的结构和性质具有重要的意义。

在材料科学、地质学、几何学等领域广泛使用。

欧拉角转换为密勒指数欧拉角的定义和表示欧拉角的定义已在前面进行了介绍，它由三个分量α、β和γ表示旋转角度，分别绕X、Y和Z轴进行旋转。

在某些特定的情况下，欧拉角可以通过旋转矩阵进行表示。

欧拉角与旋转矩阵的关系欧拉角和旋转矩阵之间存在一定的关系，通过旋转矩阵可以将欧拉角转换为旋转矢量，从而方便进行计算。

旋转矩阵和晶体学坐标系的关系旋转矩阵可以用来表示物体在空间中的旋转，包括欧拉角的旋转。

在晶体学中，晶体学坐标系是用来描述晶体中晶面方向和晶面间夹角的坐标系。

密勒指数的定义和表示密勒指数是用来描述晶体中的晶面方向的方法，它由一组整数表示。

密勒指数的每个整数表示晶面与晶体学坐标轴的交点所位于的位置。

密勒指数的计算方法密勒指数的计算方法可以通过晶面的法向量和晶体学坐标轴的关系进行计算，通过计算得到的法向量的坐标即可表示晶面的密勒指数。

欧拉角转换为密勒指数的步骤欧拉角转换为密勒指数的步骤如下： 1. 计算出旋转矩阵； 2. 确定晶体学坐标系；3. 将旋转矩阵与晶体学坐标系进行相乘，得到变换后的晶面方向；4. 通过计算得到的晶面法向量的坐标即可得到密勒指数。

欧拉角转换为密勒指数的示例以某个特定的晶体为例，假设欧拉角为α=30°，β=45°，γ=60°，晶体学坐标系为XYZ。

欧拉角转向量的计算方法改进1. 引言欧拉角是一种常用的方式来描述物体在三维空间中的姿态和旋转。

然而，在使用欧拉角进行计算时，常常会遇到一些困难，尤其在转换为向量表示时。

本文将探讨欧拉角转向量的计算方法，并提出一种改进的方法。

2. 基本概念在介绍欧拉角转向量的计算方法之前，我们先回顾一下基本的概念。

2.1 欧拉角表示欧拉角通常由三个独立的角度组成，分别表示绕固定的坐标轴进行旋转。

常用的表示方式有欧拉角顺序（XYZ、XZY、YXZ等）和旋转顺序（绕X轴旋转、绕Y轴旋转、绕Z轴旋转等）。

2.2 向量表示向量是一种具有大小和方向的量，常用来表示物体的位移、速度、加速度等。

在三维空间中，向量通常由三个分量组成。

3. 欧拉角转向量的现有方法目前常用的方法是通过欧拉角的旋转矩阵来转换为向量表示。

旋转矩阵是一个3×3的矩阵，由欧拉角的三个分量组成。

通过将旋转矩阵与单位向量相乘，可以得到旋转后的向量。

然而，这种方法存在一些问题。

旋转矩阵存在奇异点，即旋转矩阵的行列式等于零，导致计算结果不唯一。

当欧拉角存在大于360度或小于0度的情况时，计算结果也不正确。

4. 改进的方法：四元数表示为了解决上述问题，我们可以使用四元数来表示欧拉角的旋转。

四元数是一种复数的扩展，由一个实部和三个虚部组成。

它可以更准确地表示旋转，并且不存在奇异点的问题。

欧拉角转向量的改进方法如下：- 将欧拉角转换为四元数表示。

这可以通过欧拉角的三个分量来计算得到。

- 接下来，将四元数表示的旋转转化为旋转矩阵。

这可以通过一些数学运算得到。

- 将旋转矩阵与单位向量相乘，得到旋转后的向量。

通过这种改进的方法，可以避免奇异点的问题，并且可以准确地计算欧拉角转向量。

5. 总结与回顾通过对欧拉角转向量的计算方法进行改进，我们能够更准确地表示物体的旋转，避免了现有方法中的问题。

使用四元数表示可以保证计算结果的唯一性，并且不会受到欧拉角范围的限制。

6. 个人观点与理解我认为使用四元数表示欧拉角的旋转是一种有效且可靠的方法。

三维坐标欧拉角变换
三维坐标的欧拉角变换指的是通过欧拉角来表示和描述三维空间中的旋转变换。

通常情况下，三维空间中的旋转可以通过绕着三个互相垂直的轴进行，这些轴通常被称为欧拉角的轴。

具体来说，三维坐标的欧拉角变换可以由以下三个欧拉角组成：
1. Roll（滚动角）：绕X轴旋转的角度。

也称为绕前后轴旋转的角度。

2. Pitch（俯仰角）：绕Y轴旋转的角度。

也称为绕左右轴旋转的角度。

3. Yaw（偏航角）：绕Z轴旋转的角度。

也称为绕上下轴旋转的角度。

这三个欧拉角可以用来描述物体相对于初始位置的旋转变换。

需要注意的是，欧拉角变换存在一个问题，即所谓的“万向节死锁”现象。

当一个物体进行连续的多次旋转操作时，有时无法准确地还原初始位置。

为了解决这个问题，可以使用四元数或旋转矩阵等其他表示方法来进行旋转变换。

欧拉角微分方程推导首先，我们来介绍一些基本概念。

在刚体运动学中，我们用欧拉角来描述刚体在空间中的方位。

欧拉角包括三个角度：滚动角（Roll），俯仰角（Pitch）和偏航角（Yaw）。

滚动角描述绕x轴的旋转，俯仰角描述绕y轴的旋转，偏航角描述绕z轴的旋转。

为了导出欧拉角微分方程，我们首先定义一个刚体的固定坐标系N和一个随体坐标系B。

固定坐标系N与刚体的质心保持静止，而随体坐标系B与刚体一起旋转。

刚体的姿态可以通过将欧拉角应用于固定坐标系N转换为随体坐标系B来表示。

现在，让我们将欧拉角定义为最小梯度旋转，即首先绕N固定坐标系的z轴旋转偏航角Ψ，然后绕上一个旋转后的y轴旋转俯仰角θ，并最后绕上两个旋转后的x轴旋转滚动角φ。

因此，我们可以通过乘积旋转矩阵将欧拉角转换为旋转矩阵：R=RφRθRΨ其中，Rφ、Rθ和RΨ分别表示绕x、y和z轴的旋转矩阵。

现在，我们需要找到欧拉角的连续微分方程。

我们假设刚体围绕其固定坐标系N的z轴旋转一个微小的角度dΨ，然后是绕上一个旋转后的y轴旋转一个微小的角度dθ，并紧接着绕上两个旋转后的x轴旋转一个微小的角度dφ。

利用旋转矩阵的微分性质，我们可以将旋转矩阵的微分表示为：dR=(1+0.5(dφ)^2+···)Rz(dΨ)·Ry(dθ)·Rx(dφ)接下来，我们需要将这个微分旋转矩阵转换为能够描述欧拉角变化的微分方程。

我们可以使用罗德里格斯公式来表示微小旋转矩阵，它是欧拉轴-角（N,θ）的数学描述。

根据罗德里格斯公式，微小旋转矩阵可以表示为：R = I + sin(θ)N + (1 - cos(θ))N^2其中，I是单位矩阵，N是定义旋转轴的单位矢量。

将这个表达式应用到微分旋转矩阵中，我们可以得到：dR = I + sin(dθ)N + (1 - cos(dθ))N^2将上述表达式代入到之前的微分旋转矩阵中，我们可以得到：dR ≈ I + sin(dφ)Nz + (1 - cos(dφ))Nz^2 · I + sin(dθ)Ny+ (1 - cos(dθ))Ny^2 · I + sin(dΨ)Nx + (1 - cos(dΨ))Nx^2化简上述方程dR≈I+dφNz+0.5(dφ)^2Nz^2+dθNy+0.5(dθ)^2Ny^2+dΨNx+0.5(d Ψ)^2Nx^2现在，我们可以将微分旋转矩阵与连续微分欧拉角之间的关系表示为：dR=I+dφNz+0.5(dφ)^2Nz^2+dθNy+0.5(dθ)^2Ny^2+dΨNx+0.5(dΨ)^2Nx^2≈RφRθRΨ通过比较上述两个表达式的各项系数，我们可以得到欧拉角微分方程：dφ=Nz^T(RθRΨ-RΨRθ)dθ=Ny^T(RΨ-RΨ^T)dΨ=Nx^T(Rφ-Rφ^T)这就是欧拉角微分方程的推导结果。

欧拉角与旋转矩阵的转换方法欧拉角与旋转矩阵是数学中重要的概念，尤其在三维图像处理和机器人领域有着广泛应用。

欧拉角是用于描述刚体在三维空间中旋转的一种参数化方法，而旋转矩阵则是用于描述刚体旋转的数学工具。

在这篇文档中，我们将介绍欧拉角和旋转矩阵的转换方法。

一、欧拉角的定义欧拉角是描述刚体在三维空间中旋转的一种参数化方法。

它由三个角度组成，分别为俯仰角、偏航角和横滚角。

俯仰角表示绕x轴旋转的角度，偏航角表示绕y轴旋转的角度，横滚角表示绕z轴旋转的角度。

根据这三个角度可以确定一个唯一的旋转序列。

在实际应用中，欧拉角通常使用Z-Y-X欧拉角（也称为yaw-pitch-roll）来表示。

它表示先绕z轴旋转一个角度φ，然后绕旋转后的y 轴旋转一个角度θ，最后绕旋转后的x轴旋转一个角度ψ，即：R=Rz(φ)Ry(θ)Rx(ψ)其中，R表示旋转矩阵，Rz、Ry、Rx分别表示绕z、y、x轴旋转的矩阵。

在三维空间中，任何旋转都可以用欧拉角来表示。

二、旋转矩阵的定义旋转矩阵是描述刚体旋转的数学工具，它是一个3×3的矩阵。

旋转矩阵有以下三个性质：（1）行列式为1： det(R)=1（2）正交矩阵： RTR=I ，其中I为单位矩阵（3）右手定则：从坐标系的正方向看去，当右手的四指指向原坐标系中第一个非零向量，而拇指所指方向与当前坐标系中该向量方向一致时，旋转矩阵R的方向满足右手定则。

矩阵R可以通过欧拉角来确定，具体方法如下：（1）Z-Y-X欧拉角：R=Rz(φ)Ry(θ)Rx(ψ)（2）Z-Y-Z欧拉角：R=Rz(φ)Ry(θ)Rz(ψ)（3）X-Y-Z欧拉角：R=Rx(ψ)Ry(θ)Rz(φ)三、欧拉角和旋转矩阵的转换方法欧拉角和旋转矩阵之间存在一种转换关系，可以通过欧拉角计算出旋转矩阵，也可以通过旋转矩阵计算出欧拉角。

下面我们分别介绍转换方法。

1. 欧拉角转换为旋转矩阵以Z-Y-X欧拉角为例，其计算公式为：Rz(φ)Ry(θ)Rx(ψ)=[cosθcosφ,cosθsinφ,-sinθ;-cosψsinφ+sinψsinθcosφ,cosψcosφ+sinψsinθsin φ,sinψcosθ;sinψsinφ+cosψsinθcosφ,-sinψcosφ+cosψsinθsinφ,cosψcosθ];从公式中可以看出，欧拉角的计算结果是一个3×3的旋转矩阵。

ue4 欧拉角转换轴角UE4（Unreal Engine 4）是一款流行的游戏开发引擎，它提供了丰富的工具和功能，以满足开发者的需求。

在UE4中，欧拉角和轴角是两种常用的旋转表示方法。

本文将重点介绍如何在UE4中进行欧拉角到轴角的转换。

欧拉角是一种描述物体旋转的方式，它由三个角度构成，分别表示绕X轴、Y轴和Z轴的旋转。

在UE4中，可以使用Rotator结构体来表示欧拉角。

Rotator结构体有三个成员变量Pitch、Yaw和Roll，分别表示绕X轴、Y轴和Z轴的旋转角度。

轴角是另一种描述旋转的方式，它由一个旋转轴和一个旋转角度构成。

在UE4中，可以使用Quat结构体来表示轴角。

Quat结构体有四个成员变量X、Y、Z和W，其中X、Y和Z表示旋转轴的坐标，而W表示旋转角度。

在UE4中，可以通过以下方式将欧拉角转换为轴角：1. 首先，创建一个Rotator对象，设置其Pitch、Yaw和Roll成员变量为欧拉角的三个角度。

2. 调用Rotator的ToQuat方法，将其转换为Quat对象。

这个方法会返回一个新的Quat对象，表示相同的旋转。

3. 最后，可以通过Quat对象的GetAngleAxis方法获取旋转轴和旋转角度。

GetAngleAxis方法返回一个float类型的旋转角度，以及一个FVector类型的旋转轴。

使用欧拉角和轴角来表示旋转的主要区别在于它们的计算方式和表示形式。

欧拉角使用欧拉旋转公式来计算旋转矩阵，然后将旋转矩阵转换为四元数。

而轴角直接使用一个旋转轴和旋转角度来表示旋转。

欧拉角的优点是直观易懂，可以通过三个角度直接描述物体的旋转情况。

但是欧拉角存在万向锁问题，即当某个角度接近90度时，会导致旋转失真。

此外，在UE4中，欧拉角的旋转顺序也会影响最终的旋转结果。

轴角的优点是没有万向锁问题，可以精确地表示旋转。

轴角的旋转轴和旋转角度可以直接使用，非常方便。

但是轴角不如欧拉角直观，需要通过额外的计算才能获得旋转矩阵或四元数。