空间直角坐标系与大地坐标系转换程序

§2.3.1 坐标系的分类正如前面所提及的,所谓坐标系指的是描述空间位置的表达形式,即采用什么方法来表示空间位置。

人们为了描述空间位置，采用了多种方法，从而也产生了不同的坐标系，如直角坐标系、极坐标系等。

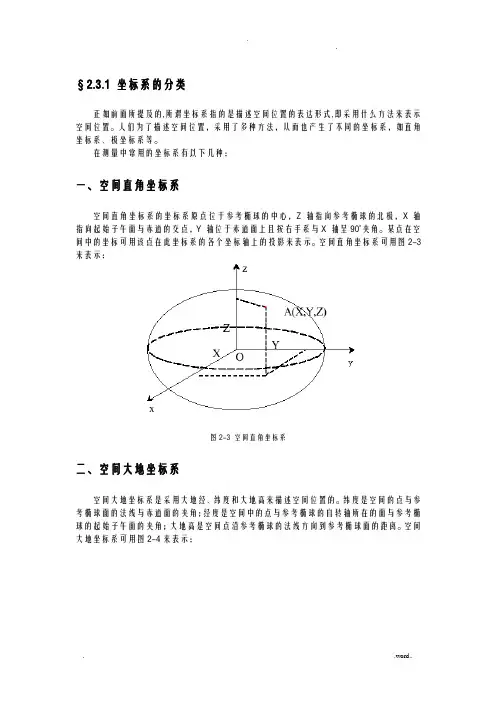
在测量中常用的坐标系有以下几种：一、空间直角坐标系空间直角坐标系的坐标系原点位于参考椭球的中心，Z 轴指向参考椭球的北极，X 轴指向起始子午面与赤道的交点，Y 轴位于赤道面上且按右手系与X 轴呈90°夹角。

某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。

空间直角坐标系可用图2-3来表示：图2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采用大地经、纬度和大地高来描述空间位置的。

纬度是空间的点与参考椭球面的法线与赤道面的夹角；经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角；大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。

空间大地坐标系可用图2-4来表示：图2-4空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换，将空间坐标空间直角坐标或空间大地坐标通过某种数学变换映射到平面上，这种变换又称为投影变换。

投影变换的方法有很多，如横轴墨卡托投影、UTM 投影、兰勃特投影等。

在我XX 用的是高斯-克吕格投影也称为高斯投影。

UTM 投影和高斯投影都是横轴墨卡托投影的特例，只是投影的个别参数不同而已。

高斯投影是一种横轴、椭圆柱面、等角投影。

从几何意义上讲，是一种横轴椭圆柱正切投影。

如图左侧所示，设想有一个椭圆柱面横套在椭球外面，并与某一子午线相切〔此子午线称为中央子午线或轴子午线〕，椭球轴的中心轴CC ’通过椭球中心而与地轴垂直。

高斯投影满足以下两个条件：1、 它是正形投影；2、 中央子午线投影后应为x 轴，且长度保持不变。

将中央子午线东西各一定经差〔一般为6度或3度〕X 围内的地区投影到椭圆柱面上，再将此柱面沿某一棱线展开，便构成了高斯平面直角坐标系，如以下图２－５右侧所示。

直角坐标系和大地坐标系的转换
在地理信息系统和测量领域中，直角坐标系和大地坐标系是两种常用的坐标系统。

直角坐标系是平面直角坐标系，由水平的x轴和垂直的y轴构成，可以用来表示平面上的点的位置，通常以米为单位。

而大地坐标系则是一种用来描述地球上点的位置的坐标系统，通常是经度（Longitude）和纬度（Latitude）的组合。

直角坐标系到大地坐标系的转换
直角坐标系到大地坐标系的转换涉及到高等数学的知识，主要是利用球面三角学的相关技巧。

在进行转换之前，需要知道点在直角坐标系中的坐标值，以及直角坐标系的原点。

然后，可以通过一系列的数学运算，将点的直角坐标值转换为大地坐标系中的经度和纬度。

大地坐标系到直角坐标系的转换
大地坐标系到直角坐标系的转换相对直接一些。

给定一个点的经度和纬度，我们可以利用地球的半径及球面三角学的相关公式，将该点的经度和纬度转换为直角坐标系中的坐标值。

这种转换可以帮助我们将地球表面上的点的位置转换为平面直角坐标系中的表示，便于进行地理信息系统中的测量和计算。

应用
直角坐标系和大地坐标系的转换在地理信息系统、地图制作、导航系统等领域都有着重要的应用。

通过这种转换，我们可以方便地将地球上的点的位置在不同坐标系统之间进行转换，从而实现不同系统之间的数据交换和信息共享。

总的来说，直角坐标系和大地坐标系的转换是地理信息系统和测量领域中的重要技术，对于地球表面上点的位置的表示和计算具有重要意义，能够为人类的地理信息分析和决策提供便利。

7.5 常用坐标系之间的关系与转换一、大地坐标系和空间大地直角坐标系及其关系大地坐标系用大地纬度企丈地经度L 和丈地髙H 来表示点的位置°这种坐标系是经 典大地测量甬:両用座标紊7屜据地图投影的理论,大地坐标系可以通过一定的投影转 化为投影平面上的直角坐标系，为地形测图和工程测量提供控制基础。

同时，这种坐标系 还是研究地球形状和大小的 种有用坐标系°所以大地坐标系在大地测量中始终有着重要 的作用.空间大地直角坐标系是-种以地球质心为原点购亘墮®坐标系，一般用X 、化Z 表 示点BSSTSTT 逐碇SS 範菇飞両H 绕禎扭转冻其轨道平面随时通过 地球质心。

对它们的跟踪观测也以地球质心为坐标原点，所以空间大地直角坐标系是卫星 大地测量中一种常用的基本坐标系。

现今，利用卫星大地测量的手段*可以迅速地测定点的空间大地直角坐拯，广泛应用于导航定位等空间技术。

同时经过数学变换，还可求岀点 的大地坐标I 用以加强和扩展地面大地网，进行岛屿和洲际联测，使传统的大地测量方法 发生了深刻的变化，所以空间大地宜角坐标系对现今大地测量的发展’具有重要的意义。

、大地坐标系和空间大地直角坐标系的转换如图7- 23所示’尸点的位置用空间 大地直角坐标〔X, Y, Z)表示，其相应 的大地坐标为(E, L)a 将该图与图？一5上式表明了 2种基本坐标系之间的关系。

加以比较可见，图7-5中的子午椭圆平面 相当于图7-23中的OJVP 平面.其中 PPz=Z.相当于图7-5中的j7；OP 3相当 丫于图7-5中的仏两平面的经度乙可视为相同，等于"叽 于是可以直接写岀X=jrcQsi f Y=jrsinL, Z=y将式(7-21).式(7-20)分别代入上式, 井考虑式(7-26)得X=Ncos^cosZr ”Y =NcQsBsinL > (7—78)Z=N (1—护〉sin^ ；BB 7-231.由大地坐标求空间大地直角坐标当已知椭球面上任一点P 的大地坐标(B, L)时，可以按式(7-78)直接求该点的 空间大地直角坐标(X, Y, Z)。

空间直角坐标系与空间大地坐标系的相互转换1.空间直角坐标系/笛卡尔坐标系坐标轴相互正交的坐标系被称作笛卡尔坐标系。

三维笛卡尔坐标系也被称为空间直角坐标系。

在空间直角坐标系下，点的坐标可以用该点所对应的矢径在三个坐标轴上的投影长度来表示，只有确定了原地、三个坐标轴的指向和尺度，就定义了一个在三维空间描述点的位置的空间直角坐标系。

以椭球体中心O为原点，起始子午面与赤道面交线为X轴，在赤道面上与X轴正交的方向为Y轴，椭球体的旋转轴为Z轴构成右手坐标系O.XYZ，在该坐标系中，P点的位置用X,Y,Z表示。

在测量应用中，常将地球空间直角坐标系的坐标原点选在地球质心（地心坐标系）或参考椭球中心（参心坐标系），z轴指向地球北极，x轴指向起始子午面与地球赤道的交点，y轴垂直于XOZ面并构成右手坐标系。

空间直角坐标系2.空间大地坐标系由于空间直角坐标无法明确反映出点与地球之间的空间关系，为了解决这一问题，在测量中引入了大地基准，并据此定义了大地坐标系。

大地基准指的是用于定义地球参考椭球的一系列参数，包括如下常量：2.1椭球的大小和形状2.2椭球的短半轴的指向：通常与地球的平自转轴平息。

2.3椭球中心的位置：根据需要确定。

若为地心椭球，则其中心位于地球质心。

2.4本初子午线：通过固定平极和经度原点的天文子午线，通常为格林尼治子午线。

以大地基准为基础建立的坐标系被称为大地坐标系。

由于大地基准又以参考椭球为基准，因此，大地坐标系又被称为椭球坐标系。

大地坐标系是参心坐标系，其坐标原点位于参考椭球中心，以参考椭球面为基准面，用大地经度L、纬度B 和大地高H表示地面点位置。

过地面点P的子午面与起始子午面间的夹角叫P 点的大地经度。

由起始子午面起算，向东为正，叫东经（0°~180°），向西为负，叫西经（0°~-180°）。

过P点的椭球法线与赤道面的夹角叫P点的大地纬度。

由赤道面起算，向北为正，叫北纬（0°~90°），向南为负，叫南纬（0°~-90°）。

高斯正反算及空间直角坐标与大地地理坐标转换一、实验目的与要求1．对以上理论内容的验证与应用。

2．通过学习掌握测绘软件开发过程与方法，初步具备测绘软件开发基本技能。

3．熟练掌握Visual C++编程环境的使用，了解其特点与程序开发过程，掌软件调试、测试的技术方法。

4．分析测绘程序设计技术课程中相关软件的结构和模块功能，掌握结构化程序设计方法和技术，掌握测绘数据处理问题的基本特点。

5．开发相关程序功能模块，独立完成相关问题概念结构分析、程序结构设计、模块设计、代码编写、调试、测试等工作。

二、实验安排1．实验时数12学时。

2．每实验小组可以由3~4人组成，或独立完成。

若由几个人完成程序设计，应进行合理的分工。

三、实验步骤和要点1．熟悉程序设计任务书的基本内容，调查了解软件需求状况，进行需求分析；2．进行总体设计。

根据所调查收集的资料和任务书的要求，对系统的硬件资源进行初步设计，提出硬件配置计划；进行软件总体设计，设计出软件程序功能的模块；3．根据总体设计的结果，进行详细设计，进行数据存储格式设计、算法等，写出逻辑代码；4．编写程序代码，调试运行；5．程序试运行。

最后同学们可根据自己的选题，写出软件开发设计书一份，打印程序代码和运行结果。

四实验原理高斯正反算:高斯正反算包括两部分内容：高斯正算和高斯反算。

简单的说就是大地地理坐标系坐标(B,L)与其对应的高斯平面直角坐标系坐标(x,y)之间的转换。

若已知大地地理坐标系坐标(B,L)解求对应的高斯平面直角坐标系坐标(x,y)称为高斯正算；反之，则为高斯反算。

空间直角坐标与大地地理坐标转换：地球表面可用一个椭球面表示。

设空间直角坐标系为OXYZ，当椭球的中心与空间直角坐标系原点重合，空间坐标系Z 轴与地球旋转重合（北极方向为正），X 轴正向经度为零时，就可以确定空间直角坐标系与大地地理坐标系的数学关系。

⎪⎩⎪⎨⎧+-=+=+=B H e N Z LB H N Y L B H N X sin ])1([sin cos )(cos cos )(2 式中 N 为卯酉圈曲率半径，B e a N 22sin 1-=； e 为椭球偏心率，222a b a e -=（a ，b 为椭球长半轴和短半轴）。

#include "stdio、h"#include "math、h"#include "stdlib、h"#include "iostream"#define PI 3、14323double a,b,c,e2,ep2;int main(){int m,n,t;double RAD(double d,double f,double m);void RBD(double hd);void BLH_XYZ();void XYZ_BLH();void B_ZS();void B_FS();void GUS_ZS();void GUS_FS();printf(" 大地测量学\n");sp1:printf("请选择功能:\n");printf("1、大地坐标系到大地空间直角坐标的转换\n");printf("2、大地空间直角坐标到大地坐标系的转换\n");printf("3、贝塞尔大地问题正算\n");printf("4、贝塞尔大地问题反算\n");printf("5、高斯投影正算\n");printf("6、高斯投影反算\n");printf("0、退出程序\n");scanf("%d",&m);if(m==0)exit(0);sp2:printf("请选择椭球参数(输入椭球序号):\n");printf("1、克拉索夫斯基椭球参数\n");printf("2、IUGG_1975椭球参数\n");printf("3、CGCS_2000椭球参数\n");printf("0、其她椭球参数(自行输入)\n");scanf("%d",&n);switch(n){case 1:a=6378245、0;b=6356863、0188;c=6399698、9018;e2=0、297;ep2=0、468;break;case 2:a=6378140、0;b=6356755、2882;c=6399596、6520;e2=0、959;ep2=0、947;break;case 3:a=6378137、0;b=6356752、3141;c=6399593、6259;e2=0、290;ep2=0、547;break;case 0:{printf("请输入椭球参数:\n");printf("长半径a=");scanf("%lf",&a);printf("短半径b=");scanf("%lf",&b);c=a*a/b;ep2=(a*a-b*b)/(b*b);e2=(a*a-b*b)/(a*a);break;}default:printf("\n\n输入错误!\n请重新输入!\n\n");goto sp2 ;}while(1){switch(m){case 1:BLH_XYZ();break;case 2:XYZ_BLH();break;case 3:B_ZS();break;case 4:B_FS();break;case 5:GUS_ZS();break;case 6:GUS_FS();break;default:printf("\n\n输入错误!\n请重新输入!\n\n");goto sp1 ;}printf("就是否继续进行此功能计算? \n\n");printf("( 若继续进行此功能计算,则输入1;\n 若选择其她功能进行计算,则输入2;\n 若退出, 则输入0、)\n");scanf("%d",&t);switch(t){case 1:break;case 2:goto sp1;case 0:exit(0);}}}double RAD(double d,double f,double m) {double e;double sign=(d<0、0)?-1、0:1、0;if(d==0){sign=(f<0、0)?-1、0:1、0;if(f==0){sign=(m<0、0)?-1、0:1、0;}}if(d<0)d=d*(-1、0);if(f<0)f=f*(-1、0);if(m<0)m=m*(-1、0);e=sign*(d*3600+f*60+m)*PI/(3600*180);return e;}void RBD(double hd){int t;int d,f;double m;double sign=(hd<0、0)?-1、0:1、0;if(hd<0)hd=fabs(hd);hd=hd*3600*180/PI;t=int(hd/3600);d=sign*t;hd=hd-t*3600;f=int(hd/60);m=hd-f*60;printf("%d'%d'%lf'\n",d,f,m);}void BLH_XYZ(){double B,L,H,N,W;double d,f,m;double X,Y,Z;printf(" 请输入大地坐标(输入格式为角度(例如:30'40'50')):\n");printf(" 大地经度L=");scanf("%lf'%lf'%lf'",&d,&f,&m);L=RAD(d,f,m);printf(" 大地纬度B=");scanf("%lf'%lf'%lf'",&d,&f,&m);B=RAD(d,f,m);printf(" 大地高H=");scanf("%lf",&H);W=sqrt(1-e2*sin(B)*sin(B));N=a/W;X=(N+H)*cos(B)*cos(L);Y=(N+H)*cos(B)*sin(L);Z=(N*(1-e2)+H)*sin(B);printf("\n\n 转换后得到大地空间直角坐标为:\n\n");printf("X=%lf\nY=%lf\nZ=%lf\n\n",X,Y,Z);}void XYZ_BLH(){double B,L,H,N,W;double X,Y,Z;double tgB0,tgB1;printf(" 请输入大地空间直角坐标:\n");printf(" X=");scanf("%lf",&X);printf(" Y=");scanf("%lf",&Y);printf(" Z=");scanf("%lf",&Z);printf("\n\n 转换后得到大地坐标为:\n\n");L=atan(Y/X);printf(" 大地经度为: L=");RBD(L);printf("\n");tgB0=Z/sqrt(X*X+Y*Y);tgB1=(1/sqrt(X*X+Y*Y))*(Z+a*e2*tgB0/sqrt(1+tgB0*tgB0-e2*tgB0*tgB0));while(fabs(tgB0-tgB1)>5*pow(10,-10)){tgB0=tgB1;tgB1=(1/sqrt(X*X+Y*Y))*(Z+a*e2*tgB0/sqrt(1+tgB0*tgB0-e2*tgB0*tgB0));}B=atan(tgB1);printf(" 大地纬度为:B=");RBD(B);printf("\n");W=sqrt(1-e2*sin(B)*sin(B));N=a/W;H=sqrt(X*X+Y*Y)/cos(B)-N;printf(" 大地高为:H=%lf\n\n",H);}void B_ZS(){double L1,B1,A1,s,d,f,mi;double u1,u2,m,M,k2,alfa,bt,r,kp2,alfap,btp,rp;double sgm0,sgm1,lmd,lmd1,lmd2,A2,B2,l,L2;printf("请输入已知点的大地坐标(输入格式为角度(例如:30'40'50'),下同):\nL1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);L1=RAD(d,f,mi);printf("\nB1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);B1=RAD(d,f,mi);printf("请输入大地方位角:\nA1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);A1=RAD(d,f,mi);printf("请输入该点至另一点的大地线长:\ns=");scanf("%lf",&s);u1=atan(sqrt(1-e2)*tan(B1));m=asin(cos(u1)*sin(A1));M=atan(tan(u1)/cos(A1));m=(m>0)?m:m+2*PI;M=(M>0)?M:M+PI;k2=ep2*cos(m)*cos(m);alfa=(1-k2/4+7*k2*k2/64-15*k2*k2*k2/256)/b;bt=k2/4-k2*k2/8+37*k2*k2*k2/512;r=k2*k2/128-k2*k2*k2/128;sgm0=alfa*s;sgm1=alfa*s+bt*sin(sgm0)*cos(2*M+sgm0)+r*sin(2*sgm0)*cos(4*M+2*sgm0); while(fabs(sgm0-sgm1)>2、8*PI/180*pow(10,-7)){sgm0=sgm1;sgm1=alfa*s+bt*sin(sgm0)*cos(2*M+sgm0)+r*sin(2*sgm0)*cos(4*M+2*sgm0); }sgm0=sgm1;A2=atan(tan(m)/cos(M+sgm0));A2=(A2>0)?A2:A2+PI;A2=(A1>PI)?A2:A2+PI;u2=atan(-cos(A2)*tan(M+sgm0));lmd1=atan(sin(u1)*tan(A1));lmd1=(lmd1>0)?lmd1:lmd1+PI;lmd1=(m<PI)?lmd1:lmd1+PI;lmd2=atan(sin(u2)*tan(A2));lmd2=(lmd2>0)?lmd2:lmd2+PI;lmd2=(m<PI)?(((M+sgm0)<PI)?lmd2:lmd2+PI):(((M+sgm0)>PI)?lmd2:lmd2+PI);lmd=lmd2-lmd1;B2=atan(sqrt(1+ep2)*tan(u2));kp2=e2*cos(m)*cos(m);alfap=(e2/2+e2*e2/8+e2*e2*e2/16)-e2/16*(1+e2)*kp2+3*e2*kp2*kp2/128;btp=e2*(1+e2)*kp2/16-e2*kp2*kp2/32;rp=e2*kp2*kp2/256;l=lmd-sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos(2*M+sgm0)+rp*sin(2*sgm0)*cos(4*M+2*sg m0));L2=L1+l;printf("\n\n得到另一点的大地坐标与大地线在该点的大地方位角为:\n\n");printf("L2=");RBD(L2);printf("\n");printf("B2=");RBD(B2);printf("\n");printf("A2=");RBD(A2);printf("\n");}void B_FS(){double L1,B1,L2,B2,s,A1,A2,du,f,mi,m0,m,M;double l,u1,u2,alfa,bt,r,lmd0,dit_lmd,lmd,sgm,dit_sgm,sgm0,sgm1,alfap,btp,rp,k2,kp2;printf("请输入第一个点大地坐标(输入格式为角度(例如:30'40'50'),下同):\n大地经度L1=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L1=RAD(du,f,mi);printf("大地纬度B1=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B1=RAD(du,f,mi);printf("\n请输入第二个点大地坐标:\n大地经度:L2=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L2=RAD(du,f,mi);printf("大地纬度:B2=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B2=RAD(du,f,mi);l=L2-L1;u1=atan(sqrt(1-e2)*tan(B1));u2=atan(sqrt(1-e2)*tan(B2));sgm0=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l));m0=asin(cos(u1)*cos(u2)*sin(l)/sin(sgm0));dit_lmd=0、003351831*sgm0*sin(m0);lmd0=l+dit_lmd;dit_sgm=sin(m0)*dit_lmd;sgm1=sgm0+dit_sgm;m=asin(cos(u1)*cos(u2)*sin(lmd0)/sin(sgm1));A1=atan(sin(lmd0)/(cos(u1)*tan(u2)-sin(u1)*cos(lmd0)));A1=(A1>0)?A1:A1+PI;A1=(m>0)?A1:A1+PI;M=atan(sin(u1)*tan(A1)/sin(m));M=(M>0)?M:M+PI;k2=ep2*cos(m)*cos(m);alfa=(1-k2/4+7*k2*k2/64-15*k2*k2*k2/256)/b;bt=k2/4-k2*k2/8+37*k2*k2*k2/512;r=k2*k2/128-k2*k2*k2/128;kp2=e2*cos(m)*cos(m);alfap=(e2/2+e2*e2/8+e2*e2*e2/16)-e2/16*(1+e2)*kp2+3*e2*kp2*kp2/128;btp=e2*(1+e2)*kp2/16-e2*kp2*kp2/32;rp=e2*kp2*kp2/256;sgm0=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l));sgm1=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l+sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos( 2*M+sgm0))));while(fabs(sgm0-sgm1)>1*PI/180*pow(10,-8)){sgm0=sgm1;sgm1=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l+sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos( 2*M+sgm0))));}sgm=sgm1;lmd=l+sin(m)*(alfap*sgm+btp*sin(sgm)*cos(2*M+sgm));s=(sgm-bt*sin(sgm)*cos(2*M+sgm)-r*sin(2*sgm)*cos(4*M+2*sgm))/alfa;A1=atan(sin(lmd)/(cos(u1)*tan(u2)-sin(u1)*cos(lmd)));A1=(A1>0)?A1:A1+PI;A1=(m>0)?A1:A1+PI;A2=atan(sin(lmd)/(sin(u2)*cos(lmd)-tan(u1)*cos(u2)));A2=(A2>0)?A2:A2+PI;A2=(m<0)?A2:A2+PI;printf("\n\n得到两点间大地线长S与大地正反方位角A1、A2如下:\n\n");printf("s=%lf\n",s);printf("A1=");RBD(A1);printf("\n");printf("A2=");RBD(A2);printf("\n");}void GUS_ZS(){double B,L,x3,x6,y3,y6,Y3,Y6,du,f,mi,X,N,n,t;double At,Bt,Ct,Dt,m3,m6,l3,l6,W,L03,L06;int DH3,DH6;printf("请输入大地坐标(输入格式为角度(例如:30'40'50')):\n大地经度L=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L=RAD(du,f,mi);printf("\n大地纬度B=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B=RAD(du,f,mi);At=1+3*e2/4+45*e2*e2/64+175*e2*e2*e2/256;Bt=3*e2/4+15*e2*e2/16+525*e2*e2*e2/512;Ct=15*e2*e2/64+105*e2*e2*e2/256;Dt=35*e2*e2*e2/512;X=a*(1-e2)*(At*B-Bt*sin(2*B)/2+Ct*sin(4*B)/4-Dt*sin(6*B)/6);W=sqrt(1-e2*sin(B)*sin(B));N=a/W;n=sqrt(ep2)*cos(B);t=tan(B);DH3=(L-(1、5*PI/180))/(3*PI/180)+1;DH6=L/(6*PI/180)+1;L03=DH3*(3*PI/180);L06=DH6*(6*PI/180)-(3*PI/180);l3=L-L03;l6=L-L06;m3=cos(B)*l3;m6=cos(B)*l6;x3=X+N*t*(m3*m3/2+(5-t*t+9*n*n+4*n*n*n*n)*m3*m3*m3*m3/24+(61-58*t*t+t*t*t*t)* m3*m3*m3*m3*m3*m3/720);x6=X+N*t*(m6*m6/2+(5-t*t+9*n*n+4*n*n*n*n)*m6*m6*m6*m6/24+(61-58*t*t+t*t*t*t)* m6*m6*m6*m6*m6*m6/720);y3=N*(m3+(1-t*t+n*n)*m3*m3*m3/6+(5-18*t*t+t*t*t*t+14*n*n-58*n*n*t*t)*m3*m3*m3 *m3*m3/120);y6=N*(m6+(1-t*t+n*n)*m6*m6*m6/6+(5-18*t*t+t*t*t*t+14*n*n-58*n*n*t*t)*m6*m6*m6 *m6*m6/120);Y3=DH3*1000000+500000+y3;Y6=DH6*1000000+500000+y6;printf("\n\n 得到的高斯平面坐标为:\n\n");printf(" 对于3度带:\n 纵坐标x=%、3lf\n 横坐标y=%、3lf(通用坐标Y=%、3lf)\n\n",x3,y3,Y3);printf(" 对于6度带:\n 纵坐标x=%、3lf\n 横坐标y=%、3lf(通用坐标Y=%、3lf)\n\n",x6,y6,Y6);}void GUS_FS(){double x,y,Y,B,B0,B1,Bf,Vf,tf,Nf,nf,L,At,Bt,Ct,Dt,L3,L6;long DH;printf(" 请输入高斯平面坐标:\n\n");printf(" 纵坐标X=");scanf("%lf",&x);printf("\n");printf(" 自然坐标y=");scanf("%lf",&y);printf("\n");printf(" 通用坐标Y=");scanf("%lf",&Y);printf("\n");At=1+3*e2/4+45*e2*e2/64+175*e2*e2*e2/256;Bt=3*e2/4+15*e2*e2/16+525*e2*e2*e2/512;Ct=15*e2*e2/64+105*e2*e2*e2/256;Dt=35*e2*e2*e2/512;B0=x/(a*(1-e2)*At);B1=(x-a*(1-e2)*(-Bt*sin(2*B0)/2+Ct*sin(4*B0)/4-Dt*sin(6*B0)/6))/(a*(1-e2)*At);while(fabs(B1-B0)>1*pow(10,-8)){B0=B1;B1=(x-a*(1-e2)*(-Bt*sin(2*B0)/2+Ct*sin(4*B0)/4-Dt*sin(6*B0)/6))/(a*(1-e2)*At);}Bf=B1;nf=sqrt(ep2)*cos(Bf);tf=tan(Bf);Vf=sqrt(1+ep2*cos(Bf)*cos(Bf));Nf=c/Vf;B=Bf-Vf*Vf*tf/2*((y/Nf)*(y/Nf)-(5+3*tf*tf+nf*nf-9*nf*nf*tf*tf)*pow((y/Nf),4)/12+(61+90*tf *tf+45*tf*tf)*pow((y/Nf),6)/360);L=((y/Nf)-(1+2*tf*tf+nf*nf)*(y/Nf)*(y/Nf)*(y/Nf)/6+(5+28*tf*tf+24*pow(tf,4)+6*nf*nf+8*nf *nf*tf*tf)*pow((y/Nf),5)/120)/cos(Bf);DH=Y/1000000;L3=3*PI/180*double(DH)+L;L6=6*PI/180*double(DH)-3*PI/180+L;printf("\n\n 得到的大地坐标为:\n\n");printf(" 大地纬度B=");RBD(B);printf("\n");printf(" 若为6度带,大地经度L=");RBD(L6);printf("\n");printf(" 若为3度带,大地经度L=");RBD(L3);printf("\n"); }。

目前国内所用GNSS (Global Navigation Satellite System)即全球卫星导航系统，已经发展到多星，尤其随着北斗导航系统的逐步完善，正在向CGCS2000椭球过渡，但还是以WGS-84 坐标系统为主流，即仍以美国GPS为主，所发布的星历参数也是基于此坐标系统。

WGS-84 坐标系统(World Geodetic System-84，世界大地坐标系-84) 的坐标原点位于地球的质心，Z 轴指向BIH1984.0定义的协议地球极方向，X 轴指向BIH1984.0的启始子午面和赤道的交点，Y 轴与X轴和Z 轴构成右手系。

WGS-84 系所采用椭球参数为：长半轴6378137;扁率1：298.25 7223563。

而我国目前广泛采用的大地测量坐标系有3种：①北京1954 坐标系。

该坐标系采用的参考椭球是克拉索夫斯基椭球，该椭球的主要参数为：长半轴6378245;扁率1：298.3。

②1980 年国家大地坐标系。

该坐标系是参心坐标系，采用地球椭球基本参数为1975 年国际大地测量与地球物理联合会第十六届大会推荐的数据，大地原点设在我国中部的陕西省泾阳县永乐镇，也称西安80 坐标系。

长半轴6378140±5;扁率1：298.257。

③2000 中国大地坐标系。

该坐标系是地心坐标系，与WGS-84坐标类似。

原点在包括海洋和大气的整个地球的质量中心;定向在1984.0时与BIH(国际时间局)。

长半轴6378137.0;扁率1：298.257 222 101。

各坐标系之间的转换是工作中的经常遇到的问题，主要的转换方法有三参数、四参数和七参数法，而这三种方法中，七参数是一种空间直角坐标系的转换模型，是基于椭球间的三维转换，精度最高。

如果用七参数法来实现WGS84 坐标系与1980 年国家大地坐标系的转换，求解前必须确定控制网中各点对的距离。

如果两点间距离超过15 公里，必须考虑曲面因素即两种不同坐标系的椭球参数，避免因椭球的差异，导致转换后所得坐标残差过大，精度过低，为了保证精度必须采用七参数法。

§2.3.1 坐标系的分类正如前面所提及的,所谓坐标系指的是描述空间位置的表达形式,即采用什么方法来表示空间位置。

人们为了描述空间位置，采用了多种方法，从而也产生了不同的坐标系，如直角坐标系、极坐标系等。

在测量中常用的坐标系有以下几种：一、空间直角坐标系空间直角坐标系的坐标系原点位于参考椭球的中心，Z 轴指向参考椭球的北极，X 轴指向起始子午面与赤道的交点，Y 轴位于赤道面上且按右手系与X 轴呈90°夹角。

某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。

空间直角坐标系可用图2-3来表示：图2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采用大地经、纬度和大地高来描述空间位置的。

纬度是空间的点与参考椭球面的法线与赤道面的夹角；经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角；大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。

空间大地坐标系可用图2-4来表示：图2-4空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换，将空间坐标空间直角坐标或空间大地坐标通过某种数学变换映射到平面上，这种变换又称为投影变换。

投影变换的方法有很多，如横轴墨卡托投影、UTM 投影、兰勃特投影等。

在我国采用的是高斯-克吕格投影也称为高斯投影。

UTM 投影和高斯投影都是横轴墨卡托投影的特例，只是投影的个别参数不同而已。

高斯投影是一种横轴、椭圆柱面、等角投影。

从几何意义上讲，是一种横轴椭圆柱正切投影。

如图左侧所示，设想有一个椭圆柱面横套在椭球外面，并与某一子午线相切（此子午线称为中央子午线或轴子午线），椭球轴的中心轴CC ’通过椭球中心而与地轴垂直。

高斯投影满足以下两个条件：1、 它是正形投影；2、 中央子午线投影后应为x 轴，且长度保持不变。

将中央子午线东西各一定经差（一般为6度或3度）范围内的地区投影到椭圆柱面上，再将此柱面沿某一棱线展开，便构成了高斯平面直角坐标系，如下图２－５右侧所示。

测绘程序设计结业考核报告大地坐标和大地空间直角坐标的互换学生姓名班级成绩指导教师(签字)地质与测绘学院测绘工程系年月日一、目的和意义坐标转换是空间实体的位置描述，是从一种坐标系统变换到另一种坐标系统的过程。

通过建立两个坐标系统之间一一对应关系来实现。

是各种比例尺地图测量和编绘中建立地图数学基础必不可少的步骤。

在实际应用中必须变换到国家统一坐标系或地方独立坐标系上来。

因此, 这种坐标转换具有很大的现实意义, 使各种测量工作得到实时、快捷的同时得到坐标系统的统一。

二、原理和过程本程序数以大地坐标和大地空间直角坐标的相互换为内容展开的，其中包括了大地坐标系转化为大地空间直角坐标系，大地空间直角坐标系转化为大地坐标系，参数设置,打开文件，保存文件等功能。

界面清晰，简洁，易懂，可视化好。

（一）原理空间直角坐标系的坐标系原点位于参考椭球的中心，Z 轴指向参考椭球的北极，X，Y 轴位于赤道面上且按右手系与X 轴呈90°夹角。

某点在空间中的坐标可轴指向起始子午面与赤道的交点用该点在此坐标系的各个坐标轴上的投影来表示。

空间直角坐标系可用图所示：空间大地坐标系是采用大地经、纬度和大地高来描述空间位置的。

纬度是空间的点与参考椭球面的法线与赤道面的夹角；经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角；大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。

空间大地坐标系可用所示：大地空间直角坐标系大地坐标系空间直角坐标系与空间大地坐标系间的转换,图表示了空间直角坐标系与空间大地坐标系之间的关系:地球空间直角坐标系与大地坐标系在相同的基准下空间大地坐标系向空间直角坐标系的转换公式为：⎪⎭⎪⎬⎫+-=+=+=B H e N Z L B H N Y L B H N X sin ])1([sin cos )(cos cos )(2 (2-1) 式中， WaN =，a 为椭球的长半轴，N 为椭球的卯酉圈曲率半径 a =6378.137km b =6356.7523141km B e W 22sin 1-=2222a b a e -=，e 为椭球的第一偏心率，b 为椭球的短半轴在相同的基准下空间直角坐标系向空间大地坐标系的转换公式为⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫-Φ=⎪⎭⎫⎝⎛=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+Φ=N B R H X Y arctg L W B Z ae tg arctg B cos cos sin 12 (2-2)式中 ⎥⎦⎤⎢⎣⎡+=Φ22YX Zarctg 222Z Y X R ++=（二）过程由源坐标类型转化为目标坐标类型，根据所选的椭球基准（椭球七参数），再计算出所需的参数，而后根据原理中的转换公式计算出所要求得的目标坐标的未知量。

7.5 常用坐标系之间的关系与转换一、大地坐标系和空间大地直角坐标系及其关系 大地坐标系用大地纬度企丈地经度L 和丈地髙H 来表示点的位置°这种坐标系是经 典大地测量甬:両用座标紊7屜据地图投影的理论,大地坐标系可以通过一定的投影转 化为投影平面上的直角坐标系，为地形测图和工程测量提供控制基础。

同时，这种坐标系 还是研究地球形状和大小的 种有用坐标系°所以大地坐标系在大地测量中始终有着重要 的作用.空间大地直角坐标系是-种以地球质心为原点购亘墮®坐标系，一般用X 、化Z 表 示点BSSTSTT 逐碇SS 範菇飞両H 绕禎扭转冻其轨道平面随时通过 地球质心。

对它们的跟踪观测也以地球质心为坐标原点，所以空间大地直角坐标系是卫星 大地测量中一种常用的基本坐标系。

现今，利用卫星大地测量的手段*可以迅速地测定点的空间大地直角坐拯，广泛应用于导航定位等空间技术。

同时经过数学变换，还可求岀点 的大地坐标I 用以加强和扩展地面大地网，进行岛屿和洲际联测，使传统的大地测量方法 发生了深刻的变化，所以空间大地宜角坐标系对现今大地测量的发展’具有重要的意义。

、大地坐标系和空间大地直角坐标系的转换如图7- 23所示’尸点的位置用空间 大地直角坐标〔X, Y, Z)表示，其相应 的大地坐标为(E, L)a 将该图与图？一5加以比较可见，图7-5中的子午椭圆平面 相当于图7-23中的OJVP 平面.其中 PPz=Z.相当于图7-5中的j7；OP 3相当 丫于图7-5中的仏两平面的经度乙可视为相同，等于"叽 于是可以直接写岀X=jrcQsi f Y=jrsinL, Z=y将式(7-21).式(7-20)分别代入上式, 井考虑式(7-26)得X=Ncos^cosZr ”Y =NcQsBsinL > (7—78)Z=N (1—护〉sin^ ；上式表明了 2种基本坐标系之间的关系。

BB 7-231.由大地坐标求空间大地直角坐标当已知椭球面上任一点P 的大地坐标(B, L)时，可以按式(7-78)直接求该点的 空间大地直角坐标(X, Y, Z)。

空间大地坐标系平面直角坐标系转换公式————————————————————————————————作者：————————————————————————————————日期：§2.3.1 坐标系的分类正如前面所提及的,所谓坐标系指的是描述空间位置的表达形式,即采用什么方法来表示空间位置。

人们为了描述空间位置，采用了多种方法，从而也产生了不同的坐标系，如直角坐标系、极坐标系等。

在测量中常用的坐标系有以下几种：一、空间直角坐标系空间直角坐标系的坐标系原点位于参考椭球的中心，Z 轴指向参考椭球的北极，X 轴指向起始子午面与赤道的交点，Y 轴位于赤道面上且按右手系与X 轴呈90°夹角。

某点在空间中的坐标可用该点在此坐标系的各个坐标轴上的投影来表示。

空间直角坐标系可用图2-3来表示：图2-3 空间直角坐标系二、空间大地坐标系空间大地坐标系是采用大地经、纬度和大地高来描述空间位置的。

纬度是空间的点与参考椭球面的法线与赤道面的夹角；经度是空间中的点与参考椭球的自转轴所在的面与参考椭球的起始子午面的夹角；大地高是空间点沿参考椭球的法线方向到参考椭球面的距离。

空间大地坐标系可用图2-4来表示：图2-4空间大地坐标系三、平面直角坐标系平面直角坐标系是利用投影变换，将空间坐标空间直角坐标或空间大地坐标通过某种数学变换映射到平面上，这种变换又称为投影变换。

投影变换的方法有很多，如横轴墨卡托投影、UTM 投影、兰勃特投影等。

在我国采用的是高斯-克吕格投影也称为高斯投影。

UTM 投影和高斯投影都是横轴墨卡托投影的特例，只是投影的个别参数不同而已。

高斯投影是一种横轴、椭圆柱面、等角投影。

从几何意义上讲，是一种横轴椭圆柱正切投影。

如图左侧所示，设想有一个椭圆柱面横套在椭球外面，并与某一子午线相切（此子午线称为中央子午线或轴子午线），椭球轴的中心轴CC ’通过椭球中心而与地轴垂直。

高斯投影满足以下两个条件： 1、 它是正形投影；2、 中央子午线投影后应为x 轴，且长度保持不变。

基于matlab的大地坐标与直角坐标间的转换第一篇：基于matlab的大地坐标与直角坐标间的转换测量程序设计实验报告换算实验名称：大地坐标与空间直角坐标的实验四大地坐标与空间直角坐标的换算一、实验目的编写大地坐标与空间直角坐标相互转换的程序，并对格式化文件数据进行计算，验证程序。

二、实验内容：1、大地坐标向空间直角坐标换算转换公式：x=(N+h)cosBcosLy=(N+h)cosBsinL（1）z=[N(1-e2)+h]sinB其中：L为经度，B为纬度，h为大地高，N=a1-esinB22为卯酉圈曲率半径，e=a2-b2为第一偏心率，a为旋转椭球长半轴，b为短半轴。

aWGS84椭球参数：长半轴 a=6378137 扁率 f = 1/298.257223563 根据上式创建以geo2xyz命名的函数，函数输入输出格式为 [x, y, z] = geo2xyz(L, B, h)2、空间直角坐标向大地坐标换算根据式（1）推导大地坐标向空间直角坐标转换公式：L=arctan(y/x)z+Ne2sinBB=arctan()22x+yh=x2+y2-NcosBaz注意计算纬度时需要用到迭代，可用B=arctan()作为初始值。

22bx+y创建以xyz2geo命名的函数，函数输入输出格式为 [L, B,h] = xyz2geo(x, y, z)三、实验步骤1、大地坐标向空间直角坐标换算主程序：%%大地坐标向空间直角坐标换算%函数的输入输出格式为[x,y,z]=geo2xyz(L,B,h)[filename,pathname] = uigetfile('*.txt','请选择打开的数据文件');file = [pathname, filename];data = importdata(file);L=data.data(:,1);B=data.data(:,2);h=data.data(:,3 );[x,y,z]=geo2xyz(L,B,h);A=[x,y,z];A=A';[filename_out,pathname_o ut] = uiputfile('*.txt','请选择要输出数据文件');fileout = [pathname_out, filename_out];fid = fopen(fileout,'wt');fprintf(fid,' x y zn');fprintf(fid,'%15.7f %15.7f %15.7fn',A);close('all');函数：function [x,y,z]=geo2xyz(L,B,h)%大地坐标经纬度转换成空间直角坐标 B=dms2rad(B);L=dms2rad(L);a=6378137;%a是长半轴f=1/298.257223563;%f是扁率b=a-a*f;e=sqrt(a^2-b^2)/a;N=a./(sqrt(1-e^2.*(sin(B)).^2));%N为卯酉圈半径率，e为第一偏心率x=(N+h).*cos(B).*cos(L);y=(N+h).*cos(B).*sin(L);z=(N*(1-e^2)+h).*sin(B);endfunction rad=dms2rad(jiaodu)%度分秒－>弧度（rad）degree = fix(jiaodu);mimute = fix((jiaodu-degree)*100);second =(jiaodu-degree-mimute/100)*10000;degree = degree+mimute/60+second/3600;rad=degree/180*pi;end2、空间直角坐标向大地坐标换算主程序：%% 将文件data.2.txt中的空间直角坐标系转换为大地坐标，并将计算结果按照格式存储在文件data3.txt中%data3.txt格式为：经度（ddmmss）纬度（ddmmss）大地高[filename,pathname]=uigetfile('*.txt','请选择打开的数据文件');file=[pathname,filename];data=importdata(file);x=data.data(:, 1);y=data.data(:,2);z=data.data(:,3);[L,B,H]=xyz2geo(x,y,z);[filena me_out,pathname_out] = uiputfile('*.txt','请选择要输出数据文件');fileout = [pathname_out, filename_out];fid = fopen(fileout,'wt');fprintf(fid,' 经度(ddmmss）纬度(ddmmss）大地高n');fprintf(fid,'%10.7f %10.7f %7.3fn',[L,B,H]');fclose('all');函数：function [L,B,H]=xyz2geo(x,y,z)%将直角坐标转换为大地坐标 %% 已知:WGS-84椭球参数f=1/298.257223563;%扁率f=(a-b)/a a=6378137;%长半轴b=a*(1-f);%短半轴e=(sqrt(a^2-b^2))/a;%第一偏心率%% 经度L的计算L=atan2(y,x);L=rad2dms(L);%% 纬度B的计算B0=atan2((a*z),(b.*sqrt(x.^2+y.^2)));% B初始值while 1 N=a./(sqrt(1-(e^2).*(sin(B0).^2)));%卯酉圈曲率半径N B=atan2(z+N.*(e^2).*sin(B0),(sqrt(x.^2+y.^2)));if abs(B0-B)<10^-6 break;end abs(B0-B)B0=B;end %% 大地高H的计算H=(sqrt(x.^2+y.^2))./cos(B)-N;B=degree2dms(B.*180/pi);%纬度B Endfunction dms= degree2dms(jiaodu)%度－>度分秒（dd.mmss）degree = fix(jiaodu);mimute = fix((jiaodu-degree)*60);second =((jiaodu-degree)*60-mimute)*60;dms = degree+mimute/100+second/10000;第二篇：空间坐标转换说明坐标转换说明GPS接收机接收到GPS（大地坐标：经度、纬度和高度值）信号后，并不利于显示，需要将大地坐标进行转换，现选用东北天坐标系（也叫站心坐标系）作为显示的依据。

大地坐标与直角空间坐标转换计算公式大地坐标与直角空间坐标转换计算公式一、参心大地坐标与参心空间直角坐标转换1名词解释：A ：参心空间直角坐标系：a) 以参心0为坐标原点；b) Z 轴与参考椭球的短轴（旋转轴）相重合； c) X 轴与起始子午面和赤道的交线重合；d) Y 轴在赤道面上与X 轴垂直，构成右手直角坐标系0-XYZ ； e)地面点P 的点位用（X ，Y ，Z ）表示；B ：参心大地坐标系：a)以参考椭球的中心为坐标原点，椭球的短轴与参考椭球旋转轴重合；b)大地纬度B ：以过地面点的椭球法线与椭球赤道面的夹角为大地纬度B ；c)大地经度L ：以过地面点的椭球子午面与起始子午面之间的夹角为大地经度L ；d) 大地高H ：地面点沿椭球法线至椭球面的距离为大地高H ； e)地面点的点位用（B ，L ，H ）表示。

2 参心大地坐标转换为参心空间直角坐标：+-=+=+=B H e N Z L B H N Y L B H N X sin *])1(*[sin *cos *)(cos *cos *)(2公式中，N 为椭球面卯酉圈的曲率半径，e 为椭球的第一偏心率，a 、b 椭球的长短半径，f 椭球扁率，W 为第一辅助系数a b a e 22-=或 f f e 1*2-= WaN B W e =-=22sin *1(西安80椭球参数：长半轴a=6378140±5（m ）短半轴b=6356755.2882m 扁率α=1/298.2573 参心空间直角坐标转换参心大地坐标[]NBY X H He N Y X H N Z B X YL -+=+-++==cos ))1(**)()(*arctan()arctan(22222二高斯投影及高斯直角坐标系1、高斯投影概述高斯-克吕格投影的条件：1. 是正形投影；2. 中央子午线不变形高斯投影的性质：1. 投影后角度不变；2. 长度比与点位有关，与方向无关； 3. 离中央子午线越远变形越大为控制投影后的长度变形，采用分带投影的方法。

地球岁差公转极移及空间直角坐标系与大地坐标系转换介绍摘要：岁差、章动、极移与地轴在空间的指向、与地球体的相对关系、地球绕地轴的旋转速度不断变化有关。

人们根据在不同方面应用的需要建立了多种坐标系，坐标系间彼此联系，可以相互转化。

关键词：岁差章动极移坐标系转换一、岁差地球是一个椭圆球体，而非正球体，赤道部分较为突出,两极则稍扁,太阳和月亮对赤道突出部分的吸引力大,使地轴绕黄极缓慢移动，因而表分点沿黄道以每年50″24的速度西移,大概要26000年移动一周,这即为岁差。

- 来源：中华文明实录由于太阳和月亮的引力对地球赤道的作用，使地轴在黄道轴的周围作圆锥形的运动,慢慢地向西移动,约二万六千年环绕一周，同时使春分点以每年50。

2角秒的速度向西移行，这种现象叫做岁差.—来源：汉语倒排词典太阳在黄道上每经过一个回归年的运行,比回到一年前的起点要差一段微小的距离,因此冬至点每年要向后（西)移动。

这就是“岁差"。

—来源:诸子百家大辞典天文学的基本概念之一。

指由于春分点沿黄道缓慢西移（每年约50.2″),而使回归年比恒星年短的现象.产生的原因是:日、月、行星对地球赤道凸出部质量的吸引，造成地轴(天轴）的进动,即地轴绕通过黄极的轴线按顺时针方向旋转，造成平天极绕黄极沿着一个小圆在约26000a中顺时针方向旋转一周,从而使天赤道、春分点位置发生变化。

日、月引力造成的岁差称为日月岁差；行星引力造成的岁差称为行星岁差；二者合称为总岁差。

岁差使天体在天球上的平位置发生改变，主要分量是沿黄经方向每年约增加50.2″。

在不同历元，春分点位置不同，同一恒星坐标值也不同;需把恒星位置化为属于所需的某一春分点的位置，即加上岁差改正。

设（α0，δ)为天体相对于t时的平赤道坐标,(α1,δ1）为相对于t1时的平赤道坐标,则岁差改正为式中τ=t1-t,m=ψ′ cos ε—λ′，n=ψ′sin ε，ψ′为日月岁差造成的平春分点在黄道上的运动速度,ψ′=50.3708″+0。

空间直角坐标系与大地坐标系转换程序#include<iostream>#include<cmath>#include<iomanip>using namespace std;#define PI (2.0*asin(1.0))void main(){ double a,b,c,d1,d2,f1,f2,m1,m2,B,L,H,X,Y,Z,W,N,e;//cout<<"请分别输入椭球的长半轴、短半轴（国际单位）"<<endl;//cin>>a>>b;a=6378137; //以WGS84为例b=6356752.3142;e=sqrt(a*a-b*b)/a;c=a*a/b;int x;cout<<"请输入0或1，0:大地坐标系到空间直角坐标系；1：空间直角坐标系到大地坐标系"<<endl;cin>>x;switch(x){case 0:{cout<<"请分别输入该点大地纬度、经度、大地高（国际单位,纬度经度请按度分秒，分别输入）"<<endl;cin>>d1>>f1>>m1>>d2>>f2>>m2>>H;B=PI*(d1+f1/60+m1/3600)/180;L=PI*(d2+f2/60+m2/3600)/180;W=sqrt(1-e*e*sin(B)*sin(B));N=a/W;X=(N+H)*cos(B)*cos(L);Y=(N+H)*cos(B)*sin(L);Z=(N*(1-e*e)+H)*sin(B);cout<<"空间直角坐标系中X,Y,Z，坐标值（国际单位）分别为"<<fixed<<setprecision(6)<<X<<" "<<fixed<<setprecision(6)<<Y<<" "<<fixed<<setprecision(6)<<Z<<endl;break;}case 1:{cout<<"请分别输入空间直角坐标系中X,Y,Z的值（国际单位）"<<endl;cin>>X>>Y>>Z;double t,m,n, P,k,B0;m=Z/sqrt(X*X+Y*Y); //t0B0=atan(m); //初值n=Z/sqrt(X*X+Y*Y);P=c*e*e/sqrt(X*X+Y*Y);k=1+(a*a-b*b)/(b*b);t=m+P*n/sqrt(k+n*n); //现在为t1，之后代替t2,t3...B=atan(t);W=sqrt(1-e*e*sin(B)*sin(B));N=a/W;H=Z/sin(B) - N*(1-e*e);int i;for(i=1;fabs(B-B0)>10E-10;i++)//每一次新的B与上一次计算的B比较，误差小于10E-10 rad {B0=B;n=t;t=m+P*n/sqrt(k+n*n);//迭代B=atan(t);}W=sqrt(1-e*e*sin(B)*sin(B));N=a/W;//if((X<0)&(Y>0))//L=atan(Y/X)+PI;//if((X<0)&(Y<0))// L=atan(Y/X)+PI;// if((X>0)&(Y<0))//L=2*PI-atan(Y/X);L=atan2(Y,X);H=sqrt(X*X+Y*Y)/cos(B)-N;int Bd,Bf,Ld,Lf;double Bm,Lm;B=180*B/PI;//B转化为度做单位Bd=B;Bf=(B-Bd)*60;Bm=((B-Bd)*60-Bf)*60;L=180*L/PI;//L转化为度做单位Ld=L;Lf=(L-Ld)*60;Lm=((L-Ld)*60-Lf)*60;cout<<"大地坐标系中纬度，经度，大地高（国际单位）分别为"<<Bd<<" "<<Bf<<" "<<fixed<<setprecision(6)<<Bm<<endl<<Ld<<" "<<Lf<<" "<<fixed<<setprecision(6)<<Lm<<endl<<fixed<<setprecision(6)<<H<<endl;break;}}}运行结果。

#include "stdio.h"#include "math.h"#include "stdlib.h"#include "iostream"#define PI 3.1415926535897323double a,b,c,e2,ep2;int main(){int m,n,t;double RAD(double d,double f,double m);void RBD(double hd);void BLH_XYZ();void XYZ_BLH();void B_ZS();void B_FS();void GUS_ZS();void GUS_FS();printf(" 大地测量学\n");sp1:printf("请选择功能:\n");printf("1.大地坐标系到大地空间直角坐标的转换\n");printf("2.大地空间直角坐标到大地坐标系的转换\n");printf("3.贝塞尔大地问题正算\n");printf("4.贝塞尔大地问题反算\n");printf("5.高斯投影正算\n");printf("6.高斯投影反算\n");printf("0.退出程序\n");scanf("%d",&m);if(m==0)exit(0);sp2:printf("请选择椭球参数(输入椭球序号):\n");printf("1.克拉索夫斯基椭球参数\n");printf("2.IUGG_1975椭球参数\n");printf("3.CGCS_2000椭球参数\n");printf("0.其他椭球参数(自行输入)\n");scanf("%d",&n);switch(n){case1:a=6378245.0;b=6356863.0188;c=6399698.9018;e2=0.00669342162297;ep2=0.0067385254146 8;break;case2:a=6378140.0;b=6356755.2882;c=6399596.6520;e2=0.00669438499959;ep2=0.0067395018194 7;break;case3:a=6378137.0;b=6356752.3141;c=6399593.6259;e2=0.00669438002290;ep2=0.0067394967754 7;break;case 0:{printf("请输入椭球参数：\n");printf("长半径a=");scanf("%lf",&a);printf("短半径b=");scanf("%lf",&b);c=a*a/b;ep2=(a*a-b*b)/(b*b);e2=(a*a-b*b)/(a*a);break;}default:printf("\n\n输入错误!\n请重新输入!\n\n");goto sp2 ;}while(1){switch(m){case 1:BLH_XYZ();break;case 2:XYZ_BLH();break;case 3:B_ZS();break;case 4:B_FS();break;case 5:GUS_ZS();break;case 6:GUS_FS();break;default:printf("\n\n输入错误!\n请重新输入!\n\n");goto sp1 ;}printf("是否继续进行此功能计算? \n\n");printf("（若继续进行此功能计算，则输入1；\n 若选择其他功能进行计算，则输入2；\n 若退出，则输入0. ）\n");scanf("%d",&t);switch(t){case 1:break;case 2:goto sp1;case 0:exit(0);}}}double RAD(double d,double f,double m){double e;double sign=(d<0.0)?-1.0:1.0;if(d==0){sign=(f<0.0)?-1.0:1.0;if(f==0){sign=(m<0.0)?-1.0:1.0;}}if(d<0)d=d*(-1.0);if(f<0)f=f*(-1.0);if(m<0)m=m*(-1.0);e=sign*(d*3600+f*60+m)*PI/(3600*180);return e;}void RBD(double hd){int t;int d,f;double m;double sign=(hd<0.0)?-1.0:1.0;if(hd<0)hd=fabs(hd);hd=hd*3600*180/PI;t=int(hd/3600);d=sign*t;hd=hd-t*3600;f=int(hd/60);m=hd-f*60;printf("%d'%d'%lf'\n",d,f,m);}void BLH_XYZ(){double B,L,H,N,W;double d,f,m;double X,Y,Z;printf(" 请输入大地坐标（输入格式为角度(例如：30'40'50')）：\n");printf(" 大地经度L=");scanf("%lf'%lf'%lf'",&d,&f,&m);L=RAD(d,f,m);printf(" 大地纬度B=");scanf("%lf'%lf'%lf'",&d,&f,&m);B=RAD(d,f,m);printf(" 大地高H=");scanf("%lf",&H);W=sqrt(1-e2*sin(B)*sin(B));N=a/W;X=(N+H)*cos(B)*cos(L);Y=(N+H)*cos(B)*sin(L);Z=(N*(1-e2)+H)*sin(B);printf("\n\n 转换后得到大地空间直角坐标为：\n\n");printf("X=%lf\nY=%lf\nZ=%lf\n\n",X,Y,Z);}void XYZ_BLH(){double B,L,H,N,W;double X,Y,Z;double tgB0,tgB1;printf(" 请输入大地空间直角坐标：\n");printf(" X=");scanf("%lf",&X);printf(" Y=");scanf("%lf",&Y);printf(" Z=");scanf("%lf",&Z);printf("\n\n 转换后得到大地坐标为：\n\n");L=atan(Y/X);printf(" 大地经度为：L=");RBD(L);printf("\n");tgB0=Z/sqrt(X*X+Y*Y);tgB1=(1/sqrt(X*X+Y*Y))*(Z+a*e2*tgB0/sqrt(1+tgB0*tgB0-e2*tgB0*tgB0));while(fabs(tgB0-tgB1)>5*pow(10,-10)){tgB0=tgB1;tgB1=(1/sqrt(X*X+Y*Y))*(Z+a*e2*tgB0/sqrt(1+tgB0*tgB0-e2*tgB0*tgB0));}B=atan(tgB1);printf(" 大地纬度为：B=");RBD(B);printf("\n");W=sqrt(1-e2*sin(B)*sin(B));N=a/W;H=sqrt(X*X+Y*Y)/cos(B)-N;printf(" 大地高为：H=%lf\n\n",H);}void B_ZS(){double L1,B1,A1,s,d,f,mi;double u1,u2,m,M,k2,alfa,bt,r,kp2,alfap,btp,rp;double sgm0,sgm1,lmd,lmd1,lmd2,A2,B2,l,L2;printf("请输入已知点的大地坐标（输入格式为角度(例如：30'40'50')，下同）：\nL1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);L1=RAD(d,f,mi);printf("\nB1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);B1=RAD(d,f,mi);printf("请输入大地方位角：\nA1=");scanf("%lf'%lf'%lf'",&d,&f,&mi);A1=RAD(d,f,mi);printf("请输入该点至另一点的大地线长：\ns=");scanf("%lf",&s);u1=atan(sqrt(1-e2)*tan(B1));m=asin(cos(u1)*sin(A1));M=atan(tan(u1)/cos(A1));m=(m>0)?m:m+2*PI;M=(M>0)?M:M+PI;k2=ep2*cos(m)*cos(m);alfa=(1-k2/4+7*k2*k2/64-15*k2*k2*k2/256)/b;bt=k2/4-k2*k2/8+37*k2*k2*k2/512;r=k2*k2/128-k2*k2*k2/128;sgm0=alfa*s;sgm1=alfa*s+bt*sin(sgm0)*cos(2*M+sgm0)+r*sin(2*sgm0)*cos(4*M+2*sgm0);while(fabs(sgm0-sgm1)>2.8*PI/180*pow(10,-7)){sgm0=sgm1;sgm1=alfa*s+bt*sin(sgm0)*cos(2*M+sgm0)+r*sin(2*sgm0)*cos(4*M+2*sgm0);}sgm0=sgm1;A2=atan(tan(m)/cos(M+sgm0));A2=(A2>0)?A2:A2+PI;A2=(A1>PI)?A2:A2+PI;u2=atan(-cos(A2)*tan(M+sgm0));lmd1=atan(sin(u1)*tan(A1));lmd1=(lmd1>0)?lmd1:lmd1+PI;lmd1=(m<PI)?lmd1:lmd1+PI;lmd2=atan(sin(u2)*tan(A2));lmd2=(lmd2>0)?lmd2:lmd2+PI;lmd2=(m<PI)?(((M+sgm0)<PI)?lmd2:lmd2+PI):(((M+sgm0)>PI)?lmd2:lmd2+PI);lmd=lmd2-lmd1;B2=atan(sqrt(1+ep2)*tan(u2));kp2=e2*cos(m)*cos(m);alfap=(e2/2+e2*e2/8+e2*e2*e2/16)-e2/16*(1+e2)*kp2+3*e2*kp2*kp2/128;btp=e2*(1+e2)*kp2/16-e2*kp2*kp2/32;rp=e2*kp2*kp2/256;l=lmd-sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos(2*M+sgm0)+rp*sin(2*sgm0)*cos(4*M+2*sgm0));L2=L1+l;printf("\n\n得到另一点的大地坐标和大地线在该点的大地方位角为：\n\n");printf("L2=");RBD(L2);printf("\n");printf("B2=");RBD(B2);printf("\n");printf("A2=");RBD(A2);printf("\n");}void B_FS(){double L1,B1,L2,B2,s,A1,A2,du,f,mi,m0,m,M;double l,u1,u2,alfa,bt,r,lmd0,dit_lmd,lmd,sgm,dit_sgm,sgm0,sgm1,alfap,btp,rp,k2,kp2;printf("请输入第一个点大地坐标（输入格式为角度(例如：30'40'50')，下同）：\n大地经度L1=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L1=RAD(du,f,mi);printf("大地纬度B1=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B1=RAD(du,f,mi);printf("\n请输入第二个点大地坐标：\n大地经度：L2=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L2=RAD(du,f,mi);printf("大地纬度：B2=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B2=RAD(du,f,mi);l=L2-L1;u1=atan(sqrt(1-e2)*tan(B1));u2=atan(sqrt(1-e2)*tan(B2));sgm0=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l));m0=asin(cos(u1)*cos(u2)*sin(l)/sin(sgm0));dit_lmd=0.003351831*sgm0*sin(m0);lmd0=l+dit_lmd;dit_sgm=sin(m0)*dit_lmd;sgm1=sgm0+dit_sgm;m=asin(cos(u1)*cos(u2)*sin(lmd0)/sin(sgm1));A1=atan(sin(lmd0)/(cos(u1)*tan(u2)-sin(u1)*cos(lmd0)));A1=(A1>0)?A1:A1+PI;A1=(m>0)?A1:A1+PI;M=atan(sin(u1)*tan(A1)/sin(m));M=(M>0)?M:M+PI;k2=ep2*cos(m)*cos(m);alfa=(1-k2/4+7*k2*k2/64-15*k2*k2*k2/256)/b;bt=k2/4-k2*k2/8+37*k2*k2*k2/512;r=k2*k2/128-k2*k2*k2/128;kp2=e2*cos(m)*cos(m);alfap=(e2/2+e2*e2/8+e2*e2*e2/16)-e2/16*(1+e2)*kp2+3*e2*kp2*kp2/128;btp=e2*(1+e2)*kp2/16-e2*kp2*kp2/32;rp=e2*kp2*kp2/256;sgm0=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l));sgm1=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l+sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos( 2*M+sgm0))));while(fabs(sgm0-sgm1)>1*PI/180*pow(10,-8)){sgm0=sgm1;sgm1=acos(sin(u1)*sin(u2)+cos(u1)*cos(u2)*cos(l+sin(m)*(alfap*sgm0+btp*sin(sgm0)*cos( 2*M+sgm0))));}sgm=sgm1;lmd=l+sin(m)*(alfap*sgm+btp*sin(sgm)*cos(2*M+sgm));s=(sgm-bt*sin(sgm)*cos(2*M+sgm)-r*sin(2*sgm)*cos(4*M+2*sgm))/alfa;A1=atan(sin(lmd)/(cos(u1)*tan(u2)-sin(u1)*cos(lmd)));A1=(A1>0)?A1:A1+PI;A1=(m>0)?A1:A1+PI;A2=atan(sin(lmd)/(sin(u2)*cos(lmd)-tan(u1)*cos(u2)));A2=(A2>0)?A2:A2+PI;A2=(m<0)?A2:A2+PI;printf("\n\n得到两点间大地线长S和大地正反方位角A1、A2如下：\n\n");printf("s=%lf\n",s);printf("A1=");RBD(A1);printf("\n");printf("A2=");RBD(A2);printf("\n");}void GUS_ZS(){double B,L,x3,x6,y3,y6,Y3,Y6,du,f,mi,X,N,n,t;double At,Bt,Ct,Dt,m3,m6,l3,l6,W,L03,L06;int DH3,DH6;printf("请输入大地坐标（输入格式为角度(例如：30'40'50')）：\n大地经度L=");scanf("%lf'%lf'%lf'",&du,&f,&mi);L=RAD(du,f,mi);printf("\n大地纬度B=");scanf("%lf'%lf'%lf'",&du,&f,&mi);B=RAD(du,f,mi);At=1+3*e2/4+45*e2*e2/64+175*e2*e2*e2/256;Bt=3*e2/4+15*e2*e2/16+525*e2*e2*e2/512;Ct=15*e2*e2/64+105*e2*e2*e2/256;Dt=35*e2*e2*e2/512;X=a*(1-e2)*(At*B-Bt*sin(2*B)/2+Ct*sin(4*B)/4-Dt*sin(6*B)/6);W=sqrt(1-e2*sin(B)*sin(B));N=a/W;n=sqrt(ep2)*cos(B);t=tan(B);DH3=(L-(1.5*PI/180))/(3*PI/180)+1;DH6=L/(6*PI/180)+1;L03=DH3*(3*PI/180);L06=DH6*(6*PI/180)-(3*PI/180);l3=L-L03;l6=L-L06;m3=cos(B)*l3;m6=cos(B)*l6;x3=X+N*t*(m3*m3/2+(5-t*t+9*n*n+4*n*n*n*n)*m3*m3*m3*m3/24+(61-58*t*t+t*t*t*t)*m3*m3*m3*m3*m3*m3/720);x6=X+N*t*(m6*m6/2+(5-t*t+9*n*n+4*n*n*n*n)*m6*m6*m6*m6/24+(61-58*t*t+t*t*t*t)*m6*m6*m6*m6*m6*m6/720);y3=N*(m3+(1-t*t+n*n)*m3*m3*m3/6+(5-18*t*t+t*t*t*t+14*n*n-58*n*n*t*t)*m3*m3*m3*m3*m3/120);y6=N*(m6+(1-t*t+n*n)*m6*m6*m6/6+(5-18*t*t+t*t*t*t+14*n*n-58*n*n*t*t)*m6*m6*m6*m6*m6/120);Y3=DH3*1000000+500000+y3;Y6=DH6*1000000+500000+y6;printf("\n\n 得到的高斯平面坐标为:\n\n");printf(" 对于3度带:\n 纵坐标x=%.3lf\n 横坐标y=%.3lf(通用坐标Y=%.3lf)\n\n",x3,y3,Y3);printf(" 对于6度带:\n 纵坐标x=%.3lf\n 横坐标y=%.3lf(通用坐标Y=%.3lf)\n\n",x6,y6,Y6);}void GUS_FS(){double x,y,Y,B,B0,B1,Bf,Vf,tf,Nf,nf,L,At,Bt,Ct,Dt,L3,L6;long DH;printf(" 请输入高斯平面坐标：\n\n");printf(" 纵坐标X=");scanf("%lf",&x);printf("\n");printf(" 自然坐标y=");scanf("%lf",&y);printf("\n");printf(" 通用坐标Y=");scanf("%lf",&Y);printf("\n");At=1+3*e2/4+45*e2*e2/64+175*e2*e2*e2/256;Bt=3*e2/4+15*e2*e2/16+525*e2*e2*e2/512;Ct=15*e2*e2/64+105*e2*e2*e2/256;Dt=35*e2*e2*e2/512;B0=x/(a*(1-e2)*At);B1=(x-a*(1-e2)*(-Bt*sin(2*B0)/2+Ct*sin(4*B0)/4-Dt*sin(6*B0)/6))/(a*(1-e2)*At);while(fabs(B1-B0)>1*pow(10,-8)){B0=B1;B1=(x-a*(1-e2)*(-Bt*sin(2*B0)/2+Ct*sin(4*B0)/4-Dt*sin(6*B0)/6))/(a*(1-e2)*At);}Bf=B1;nf=sqrt(ep2)*cos(Bf);tf=tan(Bf);Vf=sqrt(1+ep2*cos(Bf)*cos(Bf));Nf=c/Vf;B=Bf-Vf*Vf*tf/2*((y/Nf)*(y/Nf)-(5+3*tf*tf+nf*nf-9*nf*nf*tf*tf)*pow((y/Nf),4)/12+(61+90*tf*tf+45*tf*tf)*pow((y/Nf),6)/360);L=((y/Nf)-(1+2*tf*tf+nf*nf)*(y/Nf)*(y/Nf)*(y/Nf)/6+(5+28*tf*tf+24*pow(tf,4)+6*nf*nf+8*nf*nf*tf*tf)*po w((y/Nf),5)/120)/cos(Bf);DH=Y/1000000;L3=3*PI/180*double(DH)+L;L6=6*PI/180*double(DH)-3*PI/180+L;printf("\n\n 得到的大地坐标为:\n\n");printf(" 大地纬度B=");RBD(B);printf("\n");printf(" 若为6度带，大地经度L=");RBD(L6);printf("\n");printf(" 若为3度带，大地经度L=");RBD(L3);printf("\n");}。

空间直角坐标系与空间大地坐标系的相互转换1.空间直角坐标系/笛卡尔坐标系坐标轴相互正交的坐标系被称作笛卡尔坐标系。

三维笛卡尔坐标系也被称为空间直角坐标系。

在空间直角坐标系下，点的坐标可以用该点所对应的矢径在三个坐标轴上的投影长度来表示，只有确定了原地、三个坐标轴的指向和尺度，就定义了一个在三维空间描述点的位置的空间直角坐标系。

以椭球体中心O为原点，起始子午面与赤道面交线为X轴，在赤道面上与X轴正交的方向为Y轴，椭球体的旋转轴为Z轴构成右手坐标系O.XYZ，在该坐标系中，P点的位置用X,Y,Z表示。

在测量应用中，常将地球空间直角坐标系的坐标原点选在地球质心（地心坐标系）或参考椭球中心（参心坐标系），z轴指向地球北极，x轴指向起始子午面与地球赤道的交点，y轴垂直于XOZ面并构成右手坐标系。

空间直角坐标系2.空间大地坐标系由于空间直角坐标无法明确反映出点与地球之间的空间关系，为了解决这一问题，在测量中引入了大地基准，并据此定义了大地坐标系。

大地基准指的是用于定义地球参考椭球的一系列参数，包括如下常量：2.1椭球的大小和形状2.2椭球的短半轴的指向：通常与地球的平自转轴平息。

2.3椭球中心的位置：根据需要确定。

若为地心椭球，则其中心位于地球质心。

2.4本初子午线：通过固定平极和经度原点的天文子午线，通常为格林尼治子午线。

以大地基准为基础建立的坐标系被称为大地坐标系。

由于大地基准又以参考椭球为基准，因此，大地坐标系又被称为椭球坐标系。

大地坐标系是参心坐标系，其坐标原点位于参考椭球中心，以参考椭球面为基准面，用大地经度L、纬度B 和大地高H表示地面点位置。

过地面点P的子午面与起始子午面间的夹角叫P 点的大地经度。

由起始子午面起算，向东为正，叫东经（0°~180°），向西为负，叫西经（0°~-180°）。

过P点的椭球法线与赤道面的夹角叫P点的大地纬度。

由赤道面起算，向北为正，叫北纬（0°~90°），向南为负，叫南纬（0°~-90°）。