敏感性分析案例

2.敏感性分析敏感性分析是预测项目主要不决定因素的变化对项目评价指标（如内部收益率、净现值等）的影响，从中找出敏感因素，决定评价指标对该因素的敏感程度和项目对其变化的承受能力的一种不决定性分析主意。

敏感性分析有单因素敏感性分析和多因素敏感性分析。

通常只要去举行单因素敏感性分析。

【教材第一章案例九】背景：某投资项目的设计生产能力为年产10万台某种设备，主要经济参数的估算值为：初始投资额为1200万元，预计产品价格为40元／台，年经营成本170万元，运营年限10年，运营期末残值为100万元，基准收益率为12%，现值系数见表1-25。

表1-25现值系数表问题：1.以财务净现值为分析对象，就项目的投资额、产品价格和年经营成本等因素举行敏感性分析。

2.绘制财务净现值随投资、产品价格和年经营成本等因素的敏感性曲线图。

3.保证项目可行的前提下，计算该产品价格下浮临界百分比。

分析要点：本案例属于不决定性分析的另一种主意——敏感性分析的案例，它较为全面地考核了有关项目的投资额、单位产品价格和年经营成本发生变化时，项目投资效果变化情况分析的内容。

本案例主要解决以下两个问题：1.控制各因素变化对财务评价指标影响的计算主意，并找出其中最敏感的因素：2.利用平面直角坐标系描述投资额、单位产品价格和年经营成本等影响因素对财务评价指标影响的敏感程度。

【参考答案】问题1：1.计算初始条件下项目的净现值：NPV=-1200+(40×10-170) (P/A,12%,10)+100(P/F,12%,10)= -1200+230×5.6502+100×0.3220= -1200+1299.55+32.20= 131.75（万元）2.分离对投资额、单位产品价格和年经营成本，在初始值的基础上按照±10%、±20%的幅度变动，逐一计算出相应的净现值。

(1)投资额在±10%、±20%范围内变动NPV=-1200(1+10%)+(40×10-170)( P/A ,12%,10) +100×( P/F,12%,10) 10%= -1320+230×5.6502+100×0.3220= 11.75（万元）=-1200(1+20%)+230×5.6502+100×0.3220= -108.25（万元）NPV20%NPV= -1200(l-10%)+230×5.6502+100×0.3220=251.75（万元）-10%= -1200(1-20%)+230×5.6502+100×0.3220=371.75（万元）NPV-20%(2)单位产品价格在±10%、±20%范围内变动= -1200+[40(1+10%)×10-170]( P/A ,12%,10)+100×( P/F,12%,10) NPV10%= -1200+270×5.6502+100×0.3220= 357.75（万元）NPV= -1200+[40(1+20%)×10-170]( P/A ,12%,10)+100×( P/F,12%,10) 20%= -1200+310×5.6502+100×0.3220= 583.76（万元）= -1200+[40(1-10%)×10-170]( P/A ,12%,10)+100×( P/F,12%,10) NPV-10%= -1200+190×5.6502+100×0.3220= -94.26（万元）NPV= -1200+[40(1-20%)10-170]( P/A ,12%,10)+100×( P/F,12%,10)-20%= -1200+150×5.6502+100×0.3220= -320.27（万元）(3)年经营成本在±10%、±20%范围内变动NPV10%= -1200+[40×10-170(1+10%)](P/A ,12%,10)+100×( P/F,12%,10)= -1200+213×5.6502+100×0.3220= 35.69（万元）NPV20%= -1200+[40×10-170(1+20%)](P/A ,12%,10)+100×( P/F,12%,10)= -1200+196×5.6502+100×0.3220= -60.36（万元）= -1200+[40×10-170(1-10%)](P/A ,12%,10)+100×( P/F,12%,10) NPV-10%= -1200+247×5.6502+100×0.3220=227.80(万元)NPV= -1200+[40×10-170(1-20%)](P/A ,12%,10)+100×( P/F,12%,10) -20%= -1200+264×5.6502+100×0.3220=323.85（万元）将计算结果列于表1-26中。

步骤
选择关键因素；设定多个因素的变动范围；模拟不同因素组合的变动 情况；计算不同组合对财务指标的影响程度。
优点
考虑了多个因素的相互作用，更接近实际情况。
缺点
计算复杂，需要更多的数据和资源。
敏感性分析的局限性
假设条件的限制
敏感性分析基于假设条件进行， 如果假设条件不合理或过于简化
，分析结果可能不准确。
财务预测
预测方法
采用趋势分析法、回归分析法、 时间序列分析法等预测技术，对 未来的财务状况进行预测。
预测内容
包括营业收入、利润、现金流等 关键财务指标的预测，为企业战 略规划和决策提供依据。
预测准确性评估
对预测结果进行误差分析和可信 度评估，以提高预测的准确性和 可靠性。
敏感性分析的目的
评估关键因素变动对财务指标的影响程度。
结论与建议
根据敏感性分析结果，提出行业风险管理措施和行业可持续发展建 议。
谢谢
THANKS
敏感性分析的应用
投资项目评估
评估投资项目的风险和收益，为投资决策提供依据。
企业价值评估
考虑企业未来现金流的不确定性，更准确地评估企业 价值。
市场风险评估
分析市场需求和价格变动对企业财务状况的影响，制 定相应的市场策略。
单因素敏感性分析
定义
步骤
单因素敏感性分析是指对单一因素的变化 对财务指标的影响进行分析。
决策提供依据。
项目风险评估
识别项目风险因素
敏感性分析可以帮助企业识别项目中的关键风险因素，如市场需 求、成本等。
评估风险影响程度
通过财务评价，企业可以了解风险因素对项目财务指标的影响程度， 从而制定相应的风险应对措施。
制定风险管理策略

-900
0.7513
-676.17
4
300
200
140
-240
0.6830
-163.92
5
3
.6209
248.36
6~
00
3.8153
2289.18
合计
31
0
3360
85.94
第四步：进行生产成本增加的敏感性分析
现假定项目投产后第
表4生产成本上升5%的敏感性分析表单位：万元
年份
投资
成本
销售
收入
生产
成本
单位：万元
由表2可见当投资成本上升了15%后，净现值变为63.36万元。
当贴现率为12%时，净现值为-251.59万元，由内推法可得内部收益率:
年份
投资
成本
销售
收入
生产
成本
净现金 流里
10%贴现 系数
净现值
1
500
-500
0.9091
-454.55
2
1400
-1400贴现率为
Ri(R2Ri)——NPV—|
NPViNPV2I
即内部收益率为
第五步：进行价格下降的敏感性分析
现假定项目投产后第
此条件下计算净现值和内部收益率。
年份
投资
成本
销售
收入
生产
成本
净现金 流里
10%贴现 系数
净现值
1
500
-500
0.9091
-454.55
2
1500
-1500
0.8264
-1239.60
I
即内部收益率为
i
■
I

幼儿园教学体验：教师敏感性案例分析教师的敏感性在幼儿园教学中起着非常重要的作用。

敏感性不仅仅是对孩子的情感上的回应，更是一种对孩子需求的理解和满足。

在实际的教学中，教师的敏感性案例分析是非常关键的，下面通过一个案例来深入探讨幼儿园教学中教师敏感性的重要性。

案例：小明在幼儿园哭闹不安在幼儿园教学中，小明是一个经常哭闹不安的孩子。

他在幼儿园的第一个月，每天早上进园都会大哭，而且在课上也总是表现出焦躁不安的情绪，很难集中精力听讲或者参与活动。

这给周围的孩子和老师都带来了困扰。

敏感性案例分析：1. 观察和理解：教师首先要对小明的行为进行观察和理解。

不能仅仅停留在小明的哭闹和焦躁不安上，敏感的教师会主动去了解小明的家庭情况，是否有什么变化或者孩子本身有什么特殊的情况。

2. 理解需求：教师需要从小明的行为中理解他的需求。

或许是小明在家里遇到了一些不愉快的事情，或者是对幼儿园的适应需要一些时间。

教师的敏感性可以帮助他们更好地理解小明的内心世界和需求，给予他更多的关爱和支持。

3. 个性化教育：针对小明的特殊情况，敏感的教师会进行个性化的教育。

他们会在课堂上给予小明更多的关注和鼓励，让他感受到温暖和安全感。

也会与小明的家长进行沟通，了解家庭情况，共同为小明的适应做出努力。

对于这个案例，敏感的教师不仅仅是安慰和安抚小明，更重要的是理解他的需求并采取相应的措施。

这种敏感性不仅能够帮助小明更好地适应幼儿园生活，也能够在一定程度上缓解周围孩子和老师的困扰。

不仅仅是对小明个案，教师敏感性在幼儿园教学中有着非常广泛的应用。

在其他不同情况下，教师的敏感性同样扮演着非常重要的角色。

比如在识别孩子的学习需求、情感需求和行为需求时，敏感的教师能够更好地指导孩子的学习和成长。

对于家庭环境不同的孩子、性格特点不同的孩子，敏感的教师也能够更好地与他们沟通和教育。

总结回顾：教师的敏感性对于幼儿园教学有着至关重要的作用。

敏感的教师能够从更深的层面理解和关爱每一个孩子，给予他们更多的支持和鼓励。

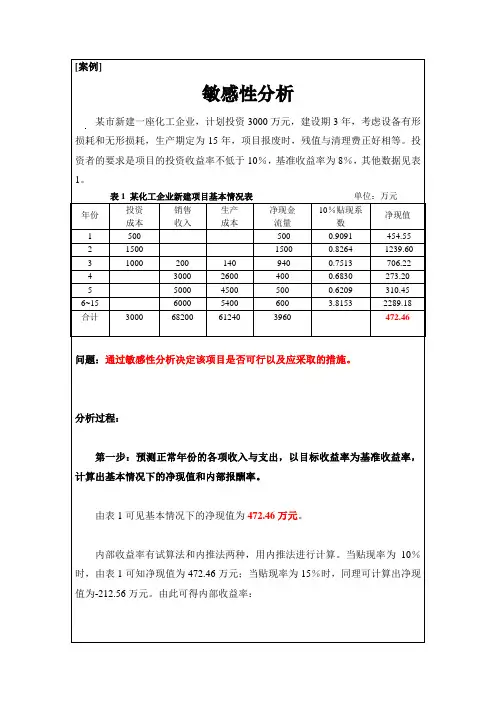
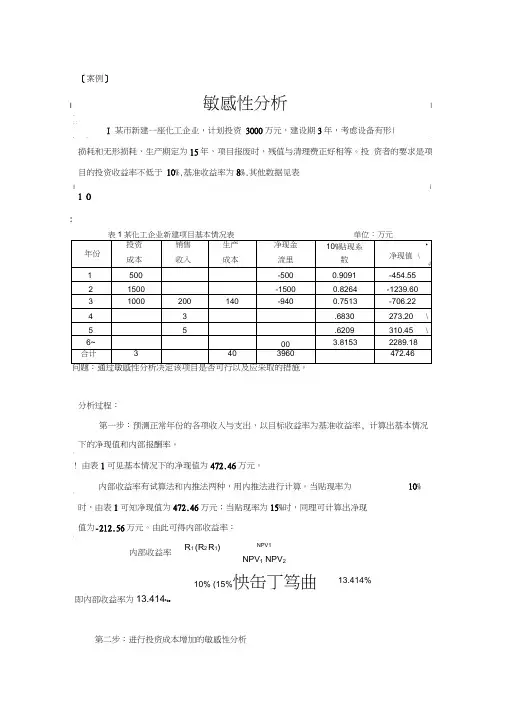
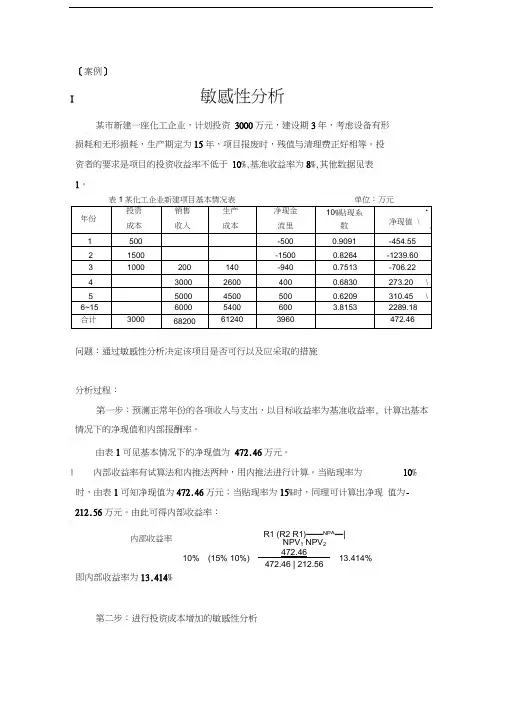
[案例]敏感性分析某市新建一座化工企业，计划投资3000万元，建设期3年，考虑设备有形损耗和无形损耗，生产期定为15年，项目报废时，残值与清理费正好相等。

投资者的要求是项目的投资收益率不低于10％，基准收益率为8％，其他数据见表1。

表1 某化工企业新建项目基本情况表单位：万元问题：通过敏感性分析决定该项目是否可行以及应采取的措施。

分析过程：第一步：预测正常年份的各项收入与支出，以目标收益率为基准收益率，计算出基本情况下的净现值和内部报酬率。

由表1可见基本情况下的净现值为472.46万元。

内部收益率有试算法和内推法两种，用内推法进行计算。

当贴现率为10％时，由表1可知净现值为472.46万元；当贴现率为15％时，同理可计算出净现值为-212.56万元。

由此可得内部收益率：%414.1356.21246.47246.472%)10%15(%10)(211121=-+-+=+-+=NPV NPV NPV R R R 内部收益率即内部收益率为13.414％。

第二步：进行投资成本增加的敏感性分析假定第一年投资成本上升了总成本的15％，在此条件下计算净现值和内部收益率。

表2 投资成本增加15％的敏感性分析表 单位：万元由表2可见当投资成本上升了15％后，净现值变为63.36万元。

当贴现率为12％时，净现值为-251.59万元，由内推法可得内部收益率：%42.1059.25136.6336.63%)10%12(%10)(211121=-+-+=+-+=NPV NPV NPV R R R 内部收益率即内部收益率为10.42％。

第三步：进行项目建设周期延长的敏感性分析现假定项目建设周期由于意外事故延长一年，并由此导致总投资增加100万元（第1、2、3和4年分别为500、1400、900和300万元），其余条件不变。

在此条件下计算净现值和内部收益率。

由表3可见当工期延长一年后，净现值变为85.94万元。

当贴现率为12％时，净现值为-205.05万元，由内推法可得内部收益率：%59.1005.20594.8594.85%)10%12(%10)(211121=-+-+=+-+=NPV NPV NPV R R R 内部收益率即内部收益率为10.59％。

假设有一个投资方案A，有关的基本数据如表1所示，方案评价所采用的折现率为20％。

表 1 A投资方案的基本数据单位：元A方案的净现值＝1400000×4.193－5000000＝870200（元）净现值大于零，说明该方案可以接受。

1.确定每年净现金流量的下限临界值。

由于：净现值为零时，X×4.193＝5000000所以：X＝1192464（元）每年净现金流量低于1192464元时，净现值为负数，方案A不可行。

每年净现金流量的变化范围为207536元（1400000元－1192464元）。

2.确定可回收期限的下限临界点。

年金现值系数＝5000000÷1400000＝3.571查表在利率20％栏内，6年的年金现值系数为3.326，7年的年金现值系数为3.605，用内插法计算投资回收年限是：投资回收年限＝6年＋12个月×（3.571－3.326）÷（3.605－3.326）＝6年11个月回收期限的变化在3年零1个月的范围内，净现值不会小于零，如果超出这一范围，则方案A不可行。

3.确定内含报酬率的变动范围。

按20％的折现率计算，有净现值870200元，说明内含报酬率一定大于20％。

确定内含报酬率的变动范围就是要计算折现率为何值时，净现值将为负数。

已知年金现值系数为3.571，查表在10年行中，25％利率的年金现值系数为 3.571，说明内含报酬率的变化范围为20％～25％之间，如对内含报酬率的要求高于25％的话，则方案A就不可行。

在实际工作中最常用的敏感性分析是分析内含报酬率指对各因素的敏感程度，具体做法是：(1)计算若干不确定因素单独变化或多因素同时变化后项目的内含报酬率，并列出敏感性分析表。

为求得不确定因素变化后的项目内含报酬率，必须按变动后的现金流量表，采用现值法，重新计算内含报酬率。

由于单位售价的变动，产品的销售收入、销售毛利、销售与管理费用中的变动成本等会引起相应的变化。

流量
10％贴现系数
净现值
1
500
-500
2
1500
-1500
3
1000
200
140
-940
4
3000
2600
400
5
5000
4500
500
6~15
6000
5670
330
合计
3000
68200
63940
1260
由表4可见当成本上升5％后，净现值变为万元。
当贴现率为5％时，净现值为万元，由内推法可得内部收益率：
表2 投资成本增加15％的敏感性分析表单位：万元
年份
投资ቤተ መጻሕፍቲ ባይዱ
成本
销售
收入
生产
成本
净现金
流量
10％贴现系数
净现值
1
950
-950
2
1500
-1500
3
1000
200
140
-940
4
3000
2600
400
5
5000
4500
500
6~15
6000
5400
600
合计
3450
68200
61240
3510
由表2可见当投资成本上升了15％后，净现值变为万元。
从总体上讲，该项目风险太大，应放弃。
[案例]
敏感性分析
某市新建一座化工企业，计划投资3000万元，建设期3年，考虑设备有形损耗和无形损耗，生产期定为15年，项目报废时，残值与清理费正好相等。投资者的要求是项目的投资收益率不低于10％，基准收益率为8％，其他数据见表1。
表1 某化工企业新建项目基本情况表单位：万元

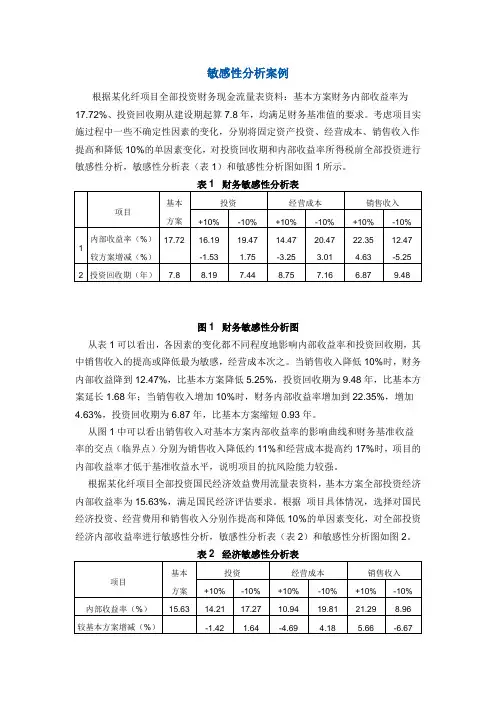
敏感性分析案例根据某化纤项目全部投资财务现金流量表资料：基本方案财务内部收益率为17.72%、投资回收期从建设期起算7.8年，均满足财务基准值的要求。

考虑项目实施过程中一些不确定性因素的变化，分别将固定资产投资、经营成本、销售收入作提高和降低10%的单因素变化，对投资回收期和内部收益率所得税前全部投资进行敏感性分析，敏感性分析表（表1）和敏感性分析图如图1所示。

图1 财务敏感性分析图从表1可以看出，各因素的变化都不同程度地影响内部收益率和投资回收期，其中销售收入的提高或降低最为敏感，经营成本次之。

当销售收入降低10%时，财务内部收益降到12.47%，比基本方案降低5.25%，投资回收期为9.48年，比基本方案延长1.68年；当销售收入增加10%时，财务内部收益率增加到22.35%，增加4.63%，投资回收期为6.87年，比基本方案缩短0.93年。

从图1中可以看出销售收入对基本方案内部收益率的影响曲线和财务基准收益率的交点（临界点）分别为销售收入降低约11%和经营成本提高约17%时，项目的内部收益率才低于基准收益水平，说明项目的抗风险能力较强。

根据某化纤项目全部投资国民经济效益费用流量表资料，基本方案全部投资经济内部收益率为15.63%，满足国民经济评估要求。

根据 项目具体情况，选择对国民经济投资、经营费用和销售收入分别作提高和降低10%的单因素变化，对全部投资经济内部收益率进行敏感性分析，敏感性分析表（表2）和敏感性分析图如图2。

图2 经济敏感性分析图从表2中可以看出，各因素的变化对内部收益率均有一定的影响，其中，销售收入的影响最大，经营费用的影响次之，投资成本的影响较小。

从图2可以看出，内部收益率达到临界点时各因素允许变化的最大幅度分别为：固定资产投资提高的临界点为28.3%，经营费用提高的临界点为7.8%，销售收入降低的临界点为5.6%。

说明该项目能承担一定的风险。

幼儿园教研案例分析：教师敏感性低的教学案例在幼儿园的教学中，教师的敏感性对于孩子的学习和成长有着至关重要的作用。

然而，也有一些教师的敏感性相对较低，在日常教学中可能存在一些问题。

本文将对教师敏感性低的教学案例进行深入分析和探讨，旨在引起对这一问题的重视并帮助教师提升自身的教学敏感性。

案例一：忽视学生情绪变化在一节幼儿园的语言课上，教师小张没有及时察觉到小玲情绪的突然变化。

小玲在课堂上突然哭闹起来，而小张却没有第一时间察觉到并采取有效的措施进行安抚和疏导。

这导致小玲的情绪没有得到及时的疏导，影响了整个课堂的教学效果。

案例分析及对策针对上述案例，我们可以看到教师在课堂上对学生情绪的敏感性相对较低。

教师在课堂上应该时刻保持对学生情绪的观察和感知，及时发现学生的情绪变化并给予适当的关怀和安抚。

教师在平时需要提升自身的情商和心理素养，以更好地应对学生的情绪问题。

案例二：对学生个体差异缺乏了解在一次幼儿园的绘画课上，教师小李并没有对孩子们的个体差异进行深入了解和照顾。

她只是简单地给孩子们布置了一幅绘画作业，并没有考虑到不同孩子的绘画兴趣和水平差异。

这导致一些孩子在课堂上表现不佳，影响了他们的学习兴趣和动力。

案例分析及对策针对这一案例，我们可以看到教师对学生个体差异的敏感性较低。

教师在教学中应该注重对学生的个体差异进行了解和照顾，针对性地进行教学设计和指导。

在绘画课上，可以根据不同孩子的兴趣和水平布置不同的绘画任务，激发孩子们的绘画潜能和兴趣。

案例三：对课堂氛围的调节能力不足在一节幼儿园的音乐课上，教师小王并没有很好地调节课堂的氛围。

课堂上有些孩子情绪比较活跃，而有些孩子则比较害羞和内向。

教师在课堂上并没有很好地对课堂氛围进行调节，导致一些孩子的参与度不高，影响了整个课堂的教学效果。

案例分析及对策针对这一案例，我们可以看到教师对课堂氛围的调节能力有所欠缺。

教师在课堂上应该根据不同孩子的个性和情绪状态，及时进行课堂氛围的调节，让每个孩子都能够愉快地参与到课堂活动中来。

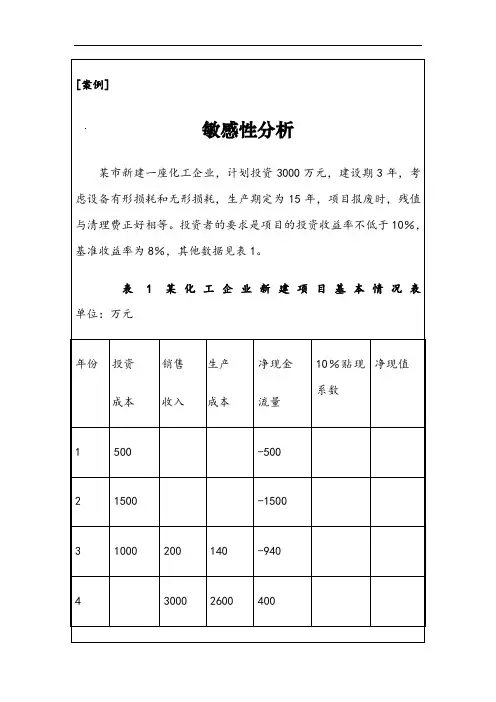
［案例］ I敏感性分析某市新建一座化工企业，计划投资 3000万元，建设期3年，考虑设备有形J:损耗和无形损耗，生产期定为15年，项目报废时，残值与清理费正好相等。

投 资者的要求是项目的投资收益率不低于 10%,基准收益率为8%,其他数据见表 1。

问题：通过敏感性分析决定该项目是否可行以及应采取的措施分析过程：第一步：预测正常年份的各项收入与支出，以目标收益率为基准收益率, 计算出基本情况下的净现值和内部报酬率。

:由表1可见基本情况下的净现值为 472.46万元。

|内部收益率有试算法和内推法两种，用内推法进行计算。

当贴现率为10%时，由表1可知净现值为472.46万元；当贴现率为15%时，同理可计算出净现 值为-212.56万元。

由此可得内部收益率：:R1 (R2 R1)——NP ^—|NPV 1 NPV 2即内部收益率为13.414%第二步：进行投资成本增加的敏感性分析内部收益率10% (15% 10%)472.46472.46 | 212.5613.414%| 假定第一年投资成本上升了总成本的 15%，在此条件下计算净现值和内部 ■收益率。

!表2投资成本增加15 %的敏感性分析表单位：万元由表2可见当投资成本上升了 15%后，净现值变为63.36万元 当贴现率为12%时，内部收益率净现值为-251.59万元,R1 (R2 R )NPV1NPV NPV 263.36 10% (12% 10%) 63.36251.5910・42%即内部收益率为10.42%i: II第三步：进行项目建设周期延长的敏感性分析I]I|现假定项目建设周期由于意外事故延长一年，并由此导致总投资增加 100万元（第1、2、3和4年分别为500、1400、900和300万元），其余条件不变。

I]I在此条件下计算净现值和内部收益率。

| 由表3可见当工期延长一年后，净现值变为 85.94万元。

II|当贴现率为12%时，1内部收益率净现值为-205.05万元，由内推法可得内部收益率:R1(R2R )NPV1NPV 1NPV2 85 94 10% (12% 10%)85.94 I 205.0510.59%■即内部收益率为10.59%表3第四步：进行生产成本增加的敏感性分析现假定项目投产后第6~15年生产成本上升5%,其余条件不变。

1、确定分析指标，如投资回收期、财务净现值、财务内部
收益率等；
2、选择需要分析的不确定性因素，如项目投资、建设周期、
项目寿命年限、成本、价格、产销量等等；
3、分析每一个不确定性因素的波动程度对分析指标的影响；
4、确定敏感性因素

敏感度系数E=△A/△F，表示项目评价指标对不确定因素

概率分析就是使用概率来研究预测不确定因
素，估算经济效率指标的数学期望、方差以及建设
项目获得某种收益可能性的大小（风险程度），从
而实现对不确定性因素的定量分析。
决策方案的分析评价可分为三种情况，即确定性、风险性和
不确定性分析。

一、确定性：制定决策的理想状态是具有确定性
(Certainty)，即由于每一方案的结果是已知的，所以管理者
已知固定成本为66000元，单位变动成本为28元，产品
单价为55元。由于成批采购材料，单位产品变动成本可
减少1‰；由于成批销售产品，单价可降低3.5‰；求利
润最大nsitivity Analysis)，就是研
究经济效果指标对影响因素的敏感性程度的大小。就
案例分析
假设有A、B、C、D四个互斥方案如果仅仅按期
望值选择， A、B、C三个方案没有区别；如果
考虑到均方差和确保盈亏平衡，则C方案最优。
在既不属于确定性情况也无法估计概率的情况下，即
处于不确定性(Uncertainty)状态，这时的选择将受决策者
心理导向的影响。乐观的管理者会选择极大极大方案；而
是研究某些影响因素，在所指定的范围内变化，而引
起目标经济效果指标的变化。

解析：
1、年度收入：75×250 ×48 ×0.75=675000

项目敏感性分析案例某城市拟新建一座大型化工企业，计划投资3000万元，建设期为3年，考虑到机器设备的有形损耗与无形损耗，生产期定为15年，项目报废时，残值与清理费正好相等。

投资者的要求是项目的投资收益率不低于12%。

试通过敏感性分析决策该项目是否可行以及应采取的措施。

该项目的敏感性分析可以分为以下六步进行：1) 预测正常年份的各项收入与支出，以目标收益率为基准收益率，计算出基本情况下的净现值和内部报酬见下表。

该项目正常情况下的净现值为正值，且数值较大。

运用内推法确定基本情况下的内部收益率，计算过程省略。

当贴现率为18%时，净现值为+188.86万元；当贴现率为20%时，净现值为-28.84万元。

选择靠近零的两组数据计算内部收益率。

内部收益率=18% + (20% - 18%)【188.86/（188.86+ | -28. 84 |）】=19. 73%从计算结果得知，正常情况下内部收益率为19.73%，高于投资者期望收益率，具有较大吸引力。

对此类项目成本效益影响较大的因素是投资成本、建设周期、生产成本和价格波动，需分别对这些因素进行敏感性分析。

2) 进行投资成本增加的敏感性分析。

假定该项目由于建筑材料涨价，导致投资成本上升15%，原来3000万元的投资额增加为3450万元，进行敏感性分析时，首先在基本情况表中对投资成本一栏加以调整，算出净现值，然后再计算内部收益率。

由于第一年投资增加450万元，净现值已由原来的1203.99万元降为802. 19万元，其内部收益率下降到16.5%，但仍高于投资者期望收益率，项目仍可实施。

3)进行项目建设周期延长的敏感性分析。

假定该项目在施工过程中，由于台风暴雨，造成部分工程返工停工，建设周期延长一年，并导致投资增加100万元，试生产和产品销售顺延一年。

计算表明，该项目对工期延长一年的敏感度不高，内部收益率在17.66%,项目可以进行。

4) 进行生产成本增加的敏感性分析。

项目投资决策——敏感性分析敏感性分析就是研究项目的评价结果对影响项目的各种因素变动敏感性的一种分析方法。

例如，当销售量、价格、成本等发生变动时，项目的净现值和内部收益率会发生不同程度的变化。

因素敏感性分析的步骤： ①选取不确定因素一般来说，投资额、产品价格、产品产量、经营成本、项目寿命期、折现率率和原材料价格等因素经常会被作为影响财务评价指标的不确定因素。

②设定不确定性因素的变化程度一般选取不确定因素变化的百分率，通常选择±5%，±10%，±15%，±20%等。

③选取分析指标敏感性分析指标就是确定要考察其不确定性的经济评价指标，一般有净现值、内部收益率和投资回收期等。

④计算敏感性指标第一，敏感度系数。

敏感度系数是反映项目效益对因素敏感程度的指标。

敏感度系数越高，敏感程度越高。

计算公式为：AE F∆=∆ 式中，E 为经济评价指标A 对因素F 的敏感度系数；F ∆为不确定性因素F 的变化率（%）；A ∆为不确定性因素F 变化F ∆时，经济评价指标A 的变化率（%）。

第二，临界点。

临界点是指项目允许不确定因素向不利方向变化的极限点。

⑤绘制敏感性分析表和敏感性分析图 ⑥对敏感性分析结果进行分析【例】 G 公司有一投资项目，其基本数据如下表所示。

假定投资额、年收入、折现率为主要的敏感性因素。

试对该投资项目净现值指标进行单因素敏感性分析。

敏感性分析基础数据解：（1）敏感性因素与分析指标已经给定，我们选取±5%，±10%作为不确定因素的变化程度。

（2）计算敏感性指标。

首先计算决策基本方案的NPV ；然后计算不同变化率下的NPV 。

NPV=-100000+(60000-20000)×(P/A ，10%，5)+10000×（P/F ，10%，5）=57840.68不确定因素变化后的取值不确定因素变化后NPV 的值当投资额的变化率为-10%时，A ∆=67840.68-57840.6857840.68= 17.3%A E F ∆=∆=17.3%-10%= -1.73其余情况计算方法类似。

经济评价敏感性案例分析摘要：结合110kV阿里塘输变电分析实例，简单介绍了工程经济评价敏感性分析方法。

主要从网售电量、静态投资、内部收益率这三个因素变动情况对项目经济评价指标的影响程度，以提高决策的准确性之外，还可以启示评价者对敏感因素进行进一步重点分析，提高其预测值的可靠性，从而达到减少项目不确定性的目的。

关键词:经济评价敏感性分析案例不确定性分析0 引言2011年我院接到110kV阿里塘输变电工程设计任务,该工程的设计工作是从可行性研究开始,历经初步设计阶段直至施工图设计完成,方可终止设计工作。

工程可行性研究就是从技术和经济两个方面分析判断该工程的可施实性。

设计人员现场踏勘后，根据工程的实际情况，做出可研设计，然后提资给技经人员做出该工程的估算，随后做出经济评价。

敏感性分析简介因为原来从没接触过经济评价,从接到这个工程任务开始，我平时就注意收集有关经济评价方面的资料，自己加强学习。

通过看书及收集资料，我知道了，电力工程经济评价原则上是属于经济学，是技术经济学的一个分支。

技术经济学是技术、经济、社会、生态及文化的交叉、渗透与综合，技术经济学是自然科学（技术）和社会科学（经济）两大学科相互交叉综合的认识上。

技术经济学作为自然科学和社会科学汇合、联盟的典范，它必然是以系统科学为指导，运用物理――事理――人理(WSR)三者有机配置的系统工程方法,研究由(科学)技术、经济、社会、生态及文化综合集成的大系统生态和文化是这个大系统的辅助子系统。

由电力技术经济学的内涵实质不难看出，电力技术经济学从经济学角度属于应用经济学，具体说来，如果技术经济学属于一级应用经济学，那么电力技术经济学作为技术经济学的一个分支学科。

由于客观条件的复杂性和人的认识能力的局限性,电力技术经济评价分析时常处于带有不确定性的环境中。

不确定性是指由于对项目有关因素或未来情况缺乏足够的情报，无法做出准确的估计，或没有全面考虑所有因素等而造成的实际价值与预期价值之间的差异。

[案例]敏感性分析某市新建一座化工企业，计划投资3000万元，建设期3年，考虑设备有形损耗和无形损耗，生产期定为15年，项目报废时，残值与清理费正好相等。

投资者的要求是项目的投资收益率不低于10％，基准收益率为8％，其他数据见表1。

表1 某化工企业新建项目基本情况表单位：万元问题：通过敏感性分析决定该项目是否可行以及应采取的措施。

分析过程：第一步：预测正常年份的各项收入与支出，以目标收益率为基准收益率，计算出基本情况下的净现值和内部报酬率。

由表1可见基本情况下的净现值为472.46万元。

内部收益率有试算法和内推法两种，用内推法进行计算。

当贴现率为10％时，由表1可知净现值为472.46万元；当贴现率为15％时，同理可计算出净现值为-212.56万元。

由此可得内部收益率：%414.1356.21246.47246.472%)10%15(%10)(211121=-+-+=+-+=NPV NPV NPV R R R 内部收益率即内部收益率为13.414％。

第二步：进行投资成本增加的敏感性分析假定第一年投资成本上升了总成本的15％，在此条件下计算净现值和内部收益率。

表2 投资成本增加15％的敏感性分析表 单位：万元由表2可见当投资成本上升了15％后，净现值变为63.36万元。

当贴现率为12％时，净现值为-251.59万元，由内推法可得内部收益率：%42.1059.25136.6336.63%)10%12(%10)(211121=-+-+=+-+=NPV NPV NPV R R R 内部收益率即内部收益率为10.42％。

第三步：进行项目建设周期延长的敏感性分析现假定项目建设周期由于意外事故延长一年，并由此导致总投资增加100万元（第1、2、3和4年分别为500、1400、900和300万元），其余条件不变。

在此条件下计算净现值和内部收益率。

由表3可见当工期延长一年后，净现值变为85.94万元。

当贴现率为12％时，净现值为-205.05万元，由内推法可得内部收益率：%59.1005.20594.8594.85%)10%12(%10)(211121=-+-+=+-+=NPV NPV NPV R R R 内部收益率即内部收益率为10.59％。

敏感性分析报告敏感性分析报告是企业、政府机关等多方面使用的一种工具，它可以帮助机构对决策方案进行全面的评估和分析。

敏感性分析报告通常根据已知和未知因素的影响程度，确定可能在最坏和最优条件下出现的各种结果，以便制定更好的计划或调整预算。

以下为三个针对不同行业的案例：1. 医疗行业：敏感性分析可以用于评估治疗方案的效率和风险。

例如，一家医院可能需要对一项新疗法进行评估，以确定其对患者健康的影响。

敏感性分析将审查各种潜在因素来确定方案的强度、疗效和费用；此外，它还会考虑不同病人的身体情况，以预测不同治疗方案的成功率。

2. 金融行业：在金融领域，敏感性分析可能用于预测市场波动或财务项目的表现。

例如，一家银行可能要了解到，如果全球利率上涨或下跌，预测将如何影响其股票价格。

通过敏感性分析，银行可根据各种情境制定不同的风险管理计划，以保护其赌注。

3. 工程领域：敏感性分析还可以用于工程项目。

例如，一个铁路公司可能对建设新线路的成本和时间表感到担忧。

该公司可以使用敏感性分析，以预测建造时间和成本风险。

与此同时，公司可以将敏感性分析结果用作规划和预算决策的依据，以确保项目成功实施。

总之，敏感性分析是一种强大的工具，许多行业都可以从中受益。

通过分析可能的结果和后果，机构和企业可以预测潜在的风险和机会，并制定相应的计划和预算。

虽然敏感性分析报告十分有用，但也存在一些限制和挑战。

首先，敏感性分析是一种预测性分析，它基于一定的假设和已有数据进行预测，因此结果可能存在误差。

其次，数据的质量和可靠性也会影响敏感性分析的实用性。

如果数据不精确或不完整，敏感性分析的结果就不足以对决策做出准确的预测。

以下是一些应对这些挑战的方法：1. 確保數據質量：以便得出準確的結論，必須確保在敏感性分析的過程中使用的數據是完整和可靠的。

可以對數據進行檢查，以確保其質量。

如果有缺陷的情況，需要調整並解決問題。

2. 基於場景分析：敏感性分析的結果會受到不確定性及環境因素的影響。

敏感因素分析案例投资回收期是一个衡量投资回报率的指标，反映了资本投资后所需要的时间段，投资获得回收。

在进行敏感性分析时，首先需要确定敏感因素。

在此方案中，敏感因素可能是售价、经营成本、产品产量。

我们分别对这三个因素进行敏感性分析。

1. 售价预计产品售价为1800元/台，如果售价波动，投资回收期会受到影响。

如果售价上升，回收期会缩短；如果售价下降，回收期将会延长。

为了方便计算，我们假设售价波动为±20%，即在1500元/台到2100元/台之间波动。

当售价为1500元/台时，每年收入为1500×1500=225万元，每年经营成本为700×1500=105万元，每年净收入为120万元。

投资回收期为800÷120=6.67年。

当售价为1800元/台时，每年收入为1800×1500=270万元，每年经营成本为700×1500=105万元，每年净收入为165万元。

投资回收期为800÷165=4.85年。

当售价为2100元/台时，每年收入为2100×1500=315万元，每年经营成本为700×1500=105万元，每年净收入为210万元。

投资回收期为800÷210=3.81年。

可以看出，售价的变动对投资回收期有着明显的影响。

2. 经营成本单位经营成本为700元/台，如果经营成本波动，投资回收期会受到影响。

如果经营成本上升，回收期将会延长；如果经营成本下降，回收期会缩短。

为了方便计算，我们假设经营成本波动为±20%，即在560元/台到840元/台之间波动。

当经营成本为560元/台时，每年经营成本为560×1500=84万元，每年净收入为66万元。

投资回收期为800÷66=12.12年。

当经营成本为700元/台时，每年经营成本为700×1500=105万元，每年净收入为60万元。