2 工程地质概述达西定律
- 格式:ppt
- 大小:810.00 KB
- 文档页数:33




简述达西定律,及达西定律的适用条件
简述达西定律,及达西定律的适用条件如下:
1、达西定律是层流条件下,土中水渗流速度与水头损失之间关系的渗流规律。
他表明在层流状态的渗流中,渗流速度与水力梯度的一次方成正比。
2、达西定律适用条件:层流状态的渗流,无论是发生于砂土或一般的粘性土中,属于层流范围,故达西定律均可适用。
但以下两种情况可认为超出达西定律适用范围。
一种情况是在纯砾以上的很粗的土中的渗流,如堆石体中的渗流,且水力坡降较大时,流态已不再是层流而是紊流。
这时,达西定律不再适用,渗流速度水力坡降之间的关系不再保持直线而变为次线性的曲线关系。

达西定律 Darcy’s Law反映水在岩土孔隙中渗流规律的实验定律。
由法国水力学家 H.-P.-G.达西在1852~1855年通过大量实验得出。
其表达式为Q=KFh/L式中Q为单位时间渗流量,F为过水断面,h为总水头损失,L为渗流路径长度,I=h/L为水力坡度,K为渗透系数。
关系式表明,水在单位时间内通过多孔介质的渗流量与渗流路径长度成反比,与过水断面面积和总水头损失成正比。
从水力学已知,通过某一断面的流量Q等于流速v与过水断面F的乘积,即Q=Fv。
或,据此,达西定律也可以用另一种形式表达v=KIv为渗流速度。
上式表明,渗流速度与水力坡度一次方成正比。
说明水力坡度与渗流速度呈线性关系,故又称线性渗流定律。
达西定律适用的上限有两种看法:一种认为达西定律适用于地下水的层流运动;另一种认为并非所有地下水层流运动都能用达西定律来表述,有些地下水层流运动的情况偏离达西定律,达西定律的适应范围比层流范围小。
这个定律说明水通过多孔介质的速度同水力梯度的大小及介质的渗透性能成正比。
这种关系可用下列方程式表示:V=K[(h2-h1)÷L]。
其中V 代表水的流速,K 代表渗透力的量度(单位与流速相同, 即长度/时间),(h2-h1)÷L 代表地下水水位的坡度(即水力梯度)。
因为摩擦的关系,地下水的运动比地表水缓慢得多。
可以利用在井中投放盐或染料,测定渗流系数和到达另一井内所需的时间。
在美国佛罗里达的含水层中,曾沿着多口水井,采用碳14 方法测定地下水的年龄。
结果测出渗流系数为每年7 米。
在渗透性能良好的介质中,渗流系数可高达每日6 米。
美国还测得过每日235 米的纪录。
不过,在许多地方,速率通常是每年不超过30 米。
达西渗流公式推导达西定律是渗流中最基本的定律, 其形式简洁( v= kJ ), 最早是由实验证实的。
它清楚地表明了渗流速度v与水力坡降J 成正比的关系。
但这里只是笼统地用k 体现不同材料的不同的渗透性。


达西定律流速-概述说明以及解释1.引言1.1 概述概述达西定律(Darcy's Law)是描述渗流运动的基本规律之一,是在地下水领域中被广泛应用的理论模型。
它是由法国工程师亨利·达西(Henry Darcy)在19世纪中期提出的,用于解析和预测地下水在多孔介质中的流动行为。
达西定律基于达西流动实验的观察结果,它指出了渗流速度与渗透系数、梯度和孔隙度之间的关系。
在达西定律中,渗透系数反映了岩石或土壤中水分传导的能力,梯度表示了水力头(水势)随空间变化的速率,而孔隙度则是指多孔介质中包含的空隙的比例。
达西定律的公式表达为:流速=渗透系数×梯度。
根据达西定律,渗流速度正比于渗透系数和水力头梯度之间的乘积。
这意味着当渗透系数增加或者水力头梯度增大时,渗流速度也会增加。
达西定律的应用领域非常广泛。
在地下水领域,它被用于研究地下水的流动和传输规律,预测地下水的补给和排泄量,评估地下水资源的可持续利用性。
而在土力学和地质工程中,达西定律则被用于分析土壤和岩石的渗流行为,帮助设计和建造地下工程结构,例如隧道、堤坝和地下储层。
然而,达西定律也存在一些局限性。
它基于一些理想假设,例如认为渗透系数是恒定的,不考虑渗透介质的非均质性和非稳定性。
因此,在实际应用中,需要结合实际情况和其他模型进行定量分析和预测。
总之,达西定律作为描述渗流规律的基础理论,对于地下水和地下工程领域的研究和应用具有重要意义。
通过深入研究和进一步探索,可以推动达西定律在实践中的应用,并促进地下水资源的合理管理和地下工程的安全可靠建设。
1.2文章结构1.2 文章结构本文将按照以下结构进行展开讨论达西定律的流速问题:第一部分是引言,将以概述的方式介绍达西定律流速的背景和相关概念。
我们将明确文章的目标和意义,为读者提供对整篇文章的整体了解。
第二部分是正文,将分为三个小节来探讨达西定律的定义和原理、应用领域以及局限性。
在2.1小节中,我们将详细介绍达西定律的定义和原理,解释其中的数学表达式和物理概念,并说明其在理解流体流动中的重要性。
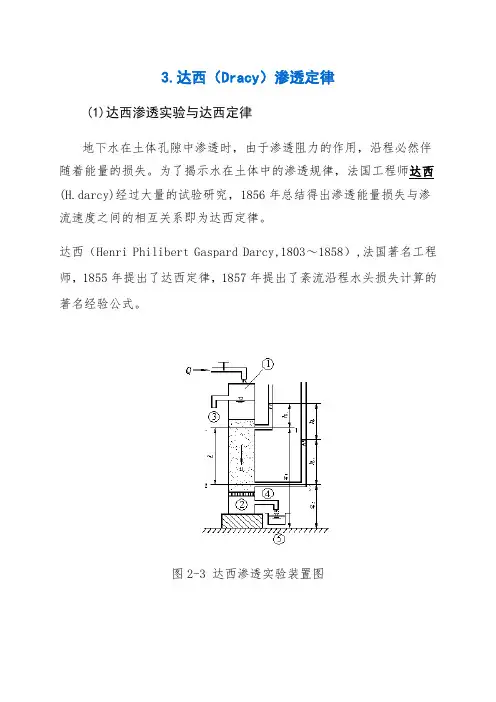
3.达西(Dracy)渗透定律(1)达西渗透实验与达西定律地下水在土体孔隙中渗透时,由于渗透阻力的作用,沿程必然伴随着能量的损失。
为了揭示水在土体中的渗透规律,法国工程师达西(H.darcy)经过大量的试验研究,1856年总结得出渗透能量损失与渗流速度之间的相互关系即为达西定律。
达西(Henri Philibert Gaspard Darcy,1803~1858),法国著名工程师,1855年提出了达西定律,1857年提出了紊流沿程水头损失计算的著名经验公式。
图2-3 达西渗透实验装置图达西实验的装置如图2-3所示。
装置中的①是横截面积为A的直立圆筒,其上端开口,在圆筒侧壁装有两支相距为l 的侧压管。
筒底以上一定距离处装一滤板②,滤板上填放颗粒均匀的砂土。
水由上端注入圆筒,多余的水从溢水管③溢出,使筒内的水位维持一个恒定值。
渗透过砂层的水从短水管④流入量杯⑤中,并以此来计算渗流量q。
设△t时间内流入量杯的水体体积为△V, 则渗流量为q=△V /△t。
同时读取断面1-1和段面2-2处的侧压管水头值h1,h2,Δh为两断面之间的水头损失。
达西分析了大量实验资料,发现土中渗透的渗流量q与圆筒断面积A及水头损失△h 成正比,与断面间距l成反比,即(2-1)或(2-2)式中i=△h/l,称为水力梯度,也称水力坡降;k为渗透系数,其值等于水力梯度为1时水的渗透速度,cm/s 。
式(2-1)和(2-2)所表示的关系称为达西定律,它是渗透的基本定律。
(2)达西定律的适用范围达西定律是由砂质土体实验得到的,后来推广应用于其他土体如粘土和具有细裂隙的岩石等。
进一步的研究表明,在某些条件下,渗透并不一定符合达西定律,因此在实际工作中我们还要注意达西定律的适用范围。
大量试验表明,当渗透速度较小时,渗透的沿程水头损失与流速的一次方成正比。
在一般情况下,砂土、粘土中的渗透速度很小,其渗流可以看作是一种水流流线互相平行的流动——层流,渗流运动规律符合达西定律,渗透速度v与水力梯度i的关系可在v-i坐标系中表示成一条直线,如图2-4(a)所示。

渗流力学达西定律公式
【最新版】
目录
1.渗流力学简介
2.达西定律的概念
3.达西定律的公式
4.达西定律的应用
正文
1.渗流力学简介
渗流力学是研究流体在多孔介质中渗流规律的学科,它广泛应用于地下水文学、土壤力学、水利工程等领域。
渗流力学有助于我们更好地理解和预测地下水的运动和控制,为水资源管理和开发提供科学依据。
2.达西定律的概念
达西定律是渗流力学的基本定律之一,它描述了流体在多孔介质中的渗流速度与压力差之间的关系。
简单来说,达西定律表示为:渗流速度与压力差成正比,比例常数即为多孔介质的渗透率。
3.达西定律的公式
达西定律的数学表达式为:
Q = KiA
其中,Q 表示渗流量,K 表示渗透率,i 表示压力差,A 表示多孔介质的截面积。
4.达西定律的应用
达西定律在实际工程中有广泛的应用,例如:
(1)地下水资源勘查:通过测量地下水位和计算压力差,可以估算地下水的储量和水流速度。
(2)水利工程设计:在设计水坝、水库、渠道等水利工程时,需要根据达西定律计算渗流量,以确保工程的稳定性和安全性。
(3)土壤改良:根据达西定律,可以通过改变土壤的渗透率来改善土壤的水分状况,从而提高土壤的肥力和作物产量。
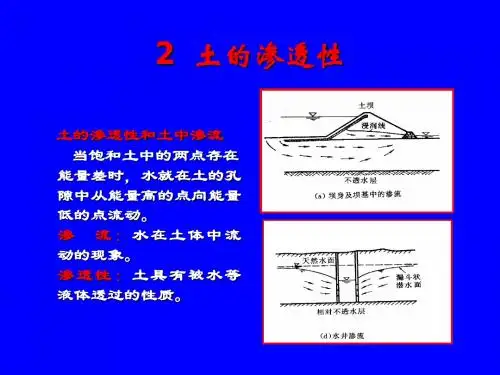

应用达西定律好的,以下是为您生成的一篇说明文:嘿,朋友!想象一下这样一个场景:在一个阳光明媚的午后,我和一群小伙伴正在探索一片神秘的土地。
那是一个正在进行大规模工程建设的地方,工人们忙忙碌碌,各种机器轰鸣作响。
在这片土地上,有一位名叫老张的工程师,他眉头紧皱,正对着一张复杂的图纸苦思冥想。
“这地下水的流动怎么就这么难以捉摸呢?”老张嘟囔着。
这时,旁边的小李凑了过来,“张工,要不试试用达西定律来分析分析?”老张眼睛一亮,仿佛在黑暗中找到了一丝曙光。
达西定律,这听起来是不是有点高大上?其实啊,它就像是我们生活中的指南针,能帮助我们搞清楚地下水在土壤或者岩石中的流动情况。
你看,就像我们在马路上行走,知道了速度和时间,就能算出走了多远。
达西定律也是这个道理,它告诉我们水在地下的流速、水力梯度和渗透系数之间的关系。
比如说,我们把地下水想象成一群调皮的孩子,它们在地下的孔隙和通道里奔跑。
水力梯度就像是给这些孩子的动力,推着它们往前跑。
而渗透系数呢,就像是地下通道的宽窄和顺畅程度。
通道宽敞又通顺,孩子们就能跑得欢快;要是又窄又堵,它们就得挤着慢慢挪。
那达西定律在实际中有啥用呢?这用处可大了去了!比如说,在修建水库的时候,工程师们得搞清楚水会不会从坝底偷偷溜走,这时候达西定律就能派上用场,帮助计算出渗漏量,从而采取有效的防渗措施。
再比如,开采地下水的时候,要知道能抽多少水而又不会导致地面下沉,达西定律也能给出答案。
在我们日常生活中,虽然我们可能不会直接用到达西定律来解决问题,但它的影响却无处不在。
就像我们呼吸的空气、喝的水,都可能与达西定律有着千丝万缕的联系。
你想想,要是没有达西定律的帮助,那些工程师们不就像没头的苍蝇,到处乱撞,找不到解决问题的方向?所以说,达西定律可真是个宝贝,为我们的生活和工程建设立下了汗马功劳!总之,达西定律在水利工程、地质勘探等领域发挥着极其重要的作用,是我们探索地下世界的有力工具。
常水头达西定律【最新版】目录1.达西定律的定义和概念2.达西定律的应用领域3.达西定律的优缺点4.达西定律的实际应用案例正文达西定律,又称为常水头达西定律,是地下水动力学中的一个基本定律。
该定律主要用于描述地下水流的基本规律,即地下水流速与水力坡度成正比。
达西定律在地下水动力学领域具有重要的理论和实践意义,被广泛应用于地下水资源的勘探、开发和管理。
达西定律的应用领域十分广泛,包括但不限于以下几个方面:首先,达西定律是地下水动力学理论体系的重要组成部分,对于研究地下水的运动规律、地下水的分布特征以及地下水的控制因素具有重要的理论意义。
其次,达西定律在实际工程应用中具有很高的实用价值。
在地下水资源的勘探中,通过测量地下水的流速和水力坡度,可以利用达西定律计算地下水的流量,从而为地下水资源的开发和利用提供科学依据。
此外,达西定律还被广泛应用于地下水污染防治领域。
通过达西定律,可以预测地下水污染的扩散速度和范围,从而为地下水污染的防治提供科学依据。
尽管达西定律在理论和实践中具有重要的意义,但它也存在一些局限性和缺点。
例如,达西定律仅适用于线性流场的地下水动力学系统,对于非线性流场的地下水动力学系统,达西定律的适用性会受到很大的限制。
此外,达西定律还存在一些假设,如流线直线、水流均匀等,这些假设在实际地下水动力学系统中可能并不成立,因此,在应用达西定律时,需要结合实际情况进行适当的修正。
在实际应用中,达西定律被广泛应用于地下水资源的开发和管理。
例如,在我国的华北平原地区,由于地下水资源的丰富,达西定律被广泛应用于地下水的勘探和开发。
通过利用达西定律,可以科学合理地开发利用地下水资源,以满足农业、工业和生活用水的需求。
总的来说,达西定律是地下水动力学领域的基本定律,它在理论研究和实际应用中都具有重要的意义。