第7章图1
- 格式:ppt
- 大小:424.00 KB
- 文档页数:7







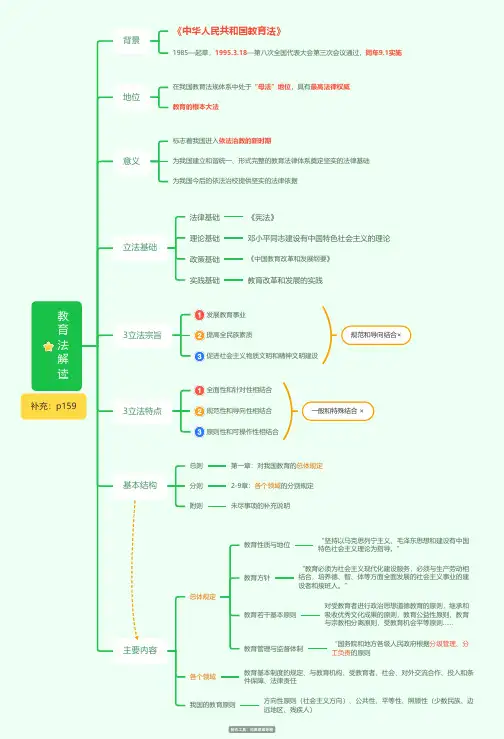
教育法解读背景《中华人民共和国教育法》1985—起草,1995.3.18—第八次全国代表大会第三次会议通过,同年9.1实施地位在我国教育法规体系中处于“母法”地位,具有最高法律权威教育的根本大法意义标志着我国进入依法治教的新时期为我国建立和谐统一、形式完整的教育法律体系奠定坚实的法律基础为我国今后的依法治校提供坚实的法律依据立法基础法律基础《宪法》理论基础邓小平同志建设有中国特色社会主义的理论政策基础《中国教育改革和发展纲要》实践基础教育改革和发展的实践3立法宗旨发展教育事业提高全民族素质促进社会主义物质文明和精神文明建设规范和导向结合×3立法特点全面性和针对性相结合规范性和导向性相结合原则性和可操作性相结合一般和特殊结合 ×基本结构总则第一章:对我国教育的总体规定分则2-9章:各个领域的分别规定附则未尽事项的补充说明主要内容总体规定教育性质与地位“坚持以马克思列宁主义、毛泽东思想和建设有中国特色社会主义理论为指导。
”教育方针“教育必须为社会主义现代化建设服务,必须与生产劳动相结合,培养德、智、体等方面全面发展的社会主义事业的建设者和接班人。
”教育若干基本原则对受教育者进行政治思想道德教育的原则,继承和吸收优秀文化成果的原则,教育公益性原则,教育与宗教相分离原则,受教育机会平等原则……教育管理与监督体制“国务院和地方各级人民政府根据分级管理、分工负责的原则各个领域教育基本制度的规定、与教育机构、受教育者、社会、对外交流合作、投入和条件保障、法律责任我国的教育原则方向性原则(社会主义方向)、公共性、平等性、照顾性(少数民族、边远地区、残疾人)补充:p159。

第7章图二.判断题部分答案解释如下。
2. 不一定是连通图,可能有若干连通分量 11. 对称矩阵可存储上(下)三角矩阵14.只有有向完全图的邻接矩阵是对称的 16. 邻接矩阵中元素值可以存储权值21. 只有无向连通图才有生成树 22. 最小生成树不唯一,但最小生成树上权值之和相等26. 是自由树,即根结点不确定35. 对有向无环图,拓扑排序成功;否则,图中有环,不能说算法不适合。
42. AOV网是用顶点代表活动,弧表示活动间的优先关系的有向图,叫顶点表示活动的网。
45. 能求出关键路径的AOE网一定是有向无环图46. 只有该关键活动为各关键路径所共有,且减少它尚不能改变关键路径的前提下,才可缩短工期。
48.按着定义,AOE网中关键路径是从“源点”到“汇点”路径长度最长的路径。
自然,关键路径上活动的时间延长多少,整个工程的时间也就随之延长多少。
三.填空题1.有n个顶点,n-1条边的无向连通图2.有向图的极大强连通子图3. 生成树9. 2(n-1) 10. N-1 11. n-1 12. n 13. N-1 14. n15. N16. 3 17. 2(N-1) 18. 度出度 19. 第I列非零元素个数 20.n 2e21.(1)查找顶点的邻接点的过程 (2)O(n+e) (3)O(n+e) (4)访问顶点的顺序不同 (5)队列和栈22. 深度优先 23.宽度优先遍历 24.队列25.因未给出存储结构,答案不唯一。
本题按邻接表存储结构,邻接点按字典序排列。
25题(1) 25题(2) 26.普里姆(prim )算法和克鲁斯卡尔(Kruskal )算法 27.克鲁斯卡尔28.边稠密 边稀疏 29. O(eloge ) 边稀疏 30.O(n 2) O(eloge) 31.(1)(V i ,V j )边上的权值 都大的数 (2)1 负值 (3)为负 边32.(1)n-1 (2)普里姆 (3)最小生成树 33.不存在环 34.递增 负值 35.16036.O(n 2) 37. 50,经过中间顶点④ 38. 75 39.O(n+e )40.(1)活动 (2)活动间的优先关系 (3)事件 (4)活动 边上的权代表活动持续时间41.关键路径 42.(1)某项活动以自己为先决条件 (2)荒谬 (3)死循环 43.(1)零 (2)V k 度减1,若V k 入度己减到零,则V k 顶点入栈 (3)环44.(1)p<>nil (2)visited[v]=true (3)p=g[v].firstarc (4)p=p^.nextarc45.(1)g[0].vexdata=v (2)g[j].firstin (3)g[j].firstin (4)g[i].firstout (5)g[i].firstout (6)p^.vexj (7)g[i].firstout (8)p:=p^.nexti (9)p<>nil (10)p^.vexj=j(11)firstadj(g,v 0) (12)not visited[w] (13)nextadj(g,v 0,w)46.(1)0 (2)j (3)i (4)0 (5)indegree[i]==0 (6)[vex][i] (7)k==1 (8)indegree[i]==047.(1)p^.link:=ch[u ].head (2)ch[u ].head:=p (3)top<>0 (4)j:=top (5)top:=ch[j].count(6)t:=t^.link48.(1)V1 V4 V3 V6 V2 V5(尽管图以邻接表为存储结构,但因没规定邻接点的排列,所以结果是不唯一的。