当前位置：文档之家 › 复变函数与积分变换1.3复数的乘幂与方根

复变函数与积分变换1.3复数的乘幂与方根

  • 格式：ppt
  • 大小：494.50 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

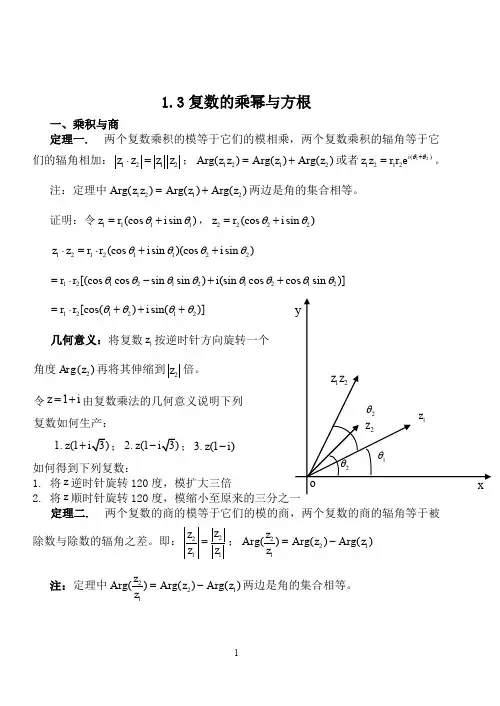
(完整word版)1.3复数的乘幂与方根

(完整word版)1.3复数的乘幂与方根

1.3复数的乘幂与方根一、乘积与商定理一.两个复数乘积的模等于它们的模相乘，两个复数乘积的辐角等于它们的辐角相加：1212z z z z ⋅=；1212rg()rg()rg()A z z A z A z =+或者12()1212i z z r r e θθ+=。

注：定理中1212rg()rg()rg()A z z A z A z =+两边是角的集合相等。

证明：令1111(cos sin )z r i θθ=+，2222(cos sin )z r i θθ=+12121122(cos sin )(cos sin )z z r r i i θθθθ⋅=⋅++1212121212[(cos cos sin sin )(sin cos cos sin )]r r i θθθθθθθθ=⋅-++ 121212[cos()sin()]r r i θθθθ=⋅+++几何意义：将复数1z 按逆时针方向旋转一个 角度2()Arg z 再将其伸缩到2z 倍。

令1z i =+由复数乘法的几何意义说明下列 复数如何生产：1.(1z +；2.(1z -；3.(1)z i -如何得到下列复数：1. 将z 逆时针旋转120度，模扩大三倍2. 将z 顺时针旋转120定理二.两个复数的商的模等于它们的模的商，两个复数的商的辐角等于被除数与除数的辐角之差。

即：2211z z z z =；2211rg()rg()rg()z A A z A z z =-注：定理中2211rg()rg()rg()z A A z A z z =-两边是角的集合相等。

证明：由除法定义21z z z =，即：21z zz =。

由定理一得：11z z z z ⋅=；11rg()rg()rg()A zz A z A z =+2211z z z z ∴=；2211rg()rg()rg()z A A z A z z =-定理一和定理二如果用复数的指数形式证明则更简单。

第一章3复数的乘幂与方根

第一章3复数的乘幂与方根
复变函数与积分变换
第二节
复数的运算
一、复数的代数运算及共轭复数的运算法则
二、复数的代数运算的几何表示
三、复数的乘幂与方根
三、复数的乘幂与方根
1. 乘幂
设复数 ≠ 0, = (cos+sin),
则 = (cosn+sinn) ，为正整数．
规定 z
−n
1
= n.
z
), w3 = 2 (cos
+ i sin
),
16
16
16
16
1
8
1
8
这四个根是内接于以原点为圆心，半径为 2的圆的正方形的顶点
8
谢谢观看！
当 = , + 1, ⋯ 时，这些根又重复出现.
=

=
1

[cos
2 在几何上，

+ 2
+ 2
+ sin
], = 0,1,2, ⋯ , − 1


1
的个值是以原点为圆心， 为
半径的圆的内接正边形的个顶点.
例3．求 1 + .
4


解： 1 + = 2(cos + sin )
特别地，当 = 1时，得到棣莫弗公式
(cos+sin) = cosn+sinn.
2. 方根
z 称为的次方根.
设 z = r (cos + i sin ), w = (cos + i sin )
方程 wn = z 的根 w ，即 w =
n
n
有 (cos n + i sin n ) = r (cos + i sin )

复变函数及其代数运算1-3

复变函数及其代数运算1-3

r 为半径的圆的内接正 n 边形的 n 个顶点.
14
例3
解
化简 (1 i )n (1 i )n .
1 1 1 i 2 i 2 2 2 cos i sin 4 4 1 1 1 i 2 i 2 2
6 i 5
,
w4 e
21
w 1 e i 1 cos i sin 1 因为 z i w 1 e 1 cos i sin 1
2 sin sin i cos 2 2 2 i tan , 2 2 cos cos i sin 2 2 2 故原方程的根为 z0 0, z1 i tan , 5 2 3 4 z2 i tan , z3 i tan , z4 i tan . 5 5 5
7
例2 已知正三角形的两个顶点为 z1 1 和z2 2 i ,
求它的另一个顶点.
解 如图所示,
o
y
z3
z2 2 i
3
x
将表示 z2 z1 的向量
z1 1 z 3 绕 z1 旋转 (或 )就得 3 3 到另一个向量, 它的终点即为所求顶点z3 (或 z ). 3
3
2 k 2 k 6 i sin 4 1 i 2 cos 4 3 3 ( k 0,1,2).
17
即 w0 2 cos i sin , 12 12
则z1 z2 r1 (cos 1 i sin 1 ) r2 (cos 2 i sin 2 )
r1 r2 [(cos 1 cos 2 sin 1 sin 2 ) i (sin 1 cos 2 cos 1 sin 2 )]

1.3 复数的乘幂与方根

1.3 复数的乘幂与方根
2π i 3 ,
π i 3 ,
2
2π 3
1
2e
2π i 3 .
13
§1.2 复数的几种表示 第 一 章
附：关于 Arg ( z1 z2 ) Arg z1 Arg z2(在集合意义下)
所谓“在集合意义下”是指：
分别从集合 Arg z1 中与集合 Arg z2 中任取一个
复 元素(即辐角)，相加后，得到集合 Arg ( z1 z2 ) 中的 数 一个元素(即辐角)。 与 复 变 比如 设 w z z , 则 | w | | z | | z | | z |2 , 函 Arg w Arg ( z z ) Arg z Arg z 2 Arg z . 数 事实上，Arg z Arg z (arg z 2k1π ) (arg z 2k2 π )
§1.3 复数的乘幂与方根
§1.3 复数的乘幂与方根 第 一 三、 复数的方根 章 2 k i( ) n n n n wk z r e , (k 0, 1,, n 1) . 复 数 描述 在复平面上， 这 n 个根均匀地 与 复 分布在一个以原点为中心、以 变 n 函 其中一个 r 为半径的圆周上。 数 根的辐角是 ( /n) . 方法
6
§1.3 复数的乘幂与方根 第 一 二、 复数的乘幂 P12 章 定义 设 z 是给定的复数， n 为正整数，n 个 z 相乘的积称为 复 n n z z z z. 记为 z , 即 复数 z 的乘幂， 数 n个 与 复 变 利用复数的指数表示式可以很快得到乘幂法则。 函 数 法则 设 z r ei , 则 z n ( r ei )n r n ei n .
2 arg z 2( k1 k2 )π 2 arg z 2k π ;

复变函数与积分变换 苏变萍_1_1.2

复变函数与积分变换 苏变萍_1_1.2
k 取其它整数时, 得到方程 wn z 的根必与这 n 个单根
1 n
中的某个重合.
1.2 复数的乘幂与方根
若设 wn e
i 2π n
, 方程 wn 1 (n 2, 3, , z 0) 的 可记为
2 n 3 n n1 n
n 个单根 1
1 n
e
i 2π n
1, wn , w , w , , w
1.2 复数的乘幂与方根
1. 复数的乘幂
对任何整数 n ,复数 z 的乘幂有： 当r 1时 即：
z r e
n n
i n
(ei )n ei n
(cos isin )n cos n isin n
此公式称为棣莫弗(De Moivre)公式.
1.2 复数的乘幂与方根
2. 复数的方根
它们是单位圆内接正 n 边形的 n 个顶点, 以 n 3 为例作图1.6，n 6 为例作图1.7.
1.2 复数的乘幂与方根
（图1.6）
（图1.7）
1.2 复数的乘幂与方根
例1.3 求 8 i 的三个三次方单根. 解： (8i) 2e
1 3 π 2 i( kπ ) 6 3
wn z 可得:
2kπ 2kπ z r cos i sin (k 0, 1, 2, ) n n
1 n 1 n
为方程 wn z 的全部根, 当 k 取 0, 1, 2, , n 1 时, 得到 方程 wn z 的 n 个单根,这 n 个单根在几何上表现为以 原点为中心 r 为半径的圆内接正 n 边形的 n 个顶点.当
(k 0, 1, 2)
例1.4 计算 1 i
3 3 π 2kπ π 2kπ 解： 1 i 4 2(cos 4 i sin 4 ) 2 2

复变函数和积分变换重要知识点归纳

复变函数和积分变换重要知识点归纳

.WORD.格式.复变函数复习重点(一)复数的概念1.复数的概念：z x iy =+，,x y 是实数,()()Re ,Im x z y z ==.21i =-.注：一般两个复数不比较大小，但其模（为实数）有大小. 2.复数的表示1）模：z=2）幅角：在0z ≠时，矢量与x 轴正向的夹角，记为()Arg z （多值函数）；主值()arg z 是位于(,]ππ-中的幅角。

3）()arg z 与arctan y x之间的关系如下：当0,x > arg arctanyz x=；当0,arg arctan 0,0,arg arctan yy z x x y y z xππ⎧≥=+⎪⎪<⎨⎪<=-⎪⎩； 4）三角表示：()cos sin z z i θθ=+，其中arg z θ=；注：中间一定是“+”号。

5）指数表示：i z z e θ=，其中arg z θ=。

(二) 复数的运算1.加减法：若111222,z x iy z x iy =+=+，则()()121212z z x x i y y ±=±+±2.乘除法：1）若111222,z x iy z x iy =+=+，则()()1212122112z z x x y y i x y x y =-++；()()()()112211112121221222222222222222x iy x iy z x iy x x y y y x y x i z x iy x iy x iy x y x y +-++-===+++-++。

2）若121122,i i z z e z z e θθ==, 则()121212i z z z z e θθ+=；()121122i z z ez z θθ-=3.乘幂与方根1） 若(cos sin )i z z i z e θθθ=+=，则(cos sin )nnn in z z n i n z e θθθ=+=。

复变函数与积分变换讲义详细.

复变函数与积分变换讲义详细.
2 2

0
x
2 2
z z r x y ----复数z的模 z与x轴正向的夹角弧度 ----复数z的辐角(argument)
记作Arg z= . 任何一个复数z0有无穷多个辐角,将满足
x
p <0p 的0 称为Arg z的主值, 记作0=arg z .则 Arg z=0+2kp =arg z +2kp (k为任意整数)
z r (cos i sin )
利用欧拉公式 e i = cos + i sin 得指数表示式:
z re
i
(r z , Arg z )
例1 将下列复数化为三角表示式与指数表示式.
1) z 12 2i; 2) z sin
[解] 1)
i cos . 5 5 r | z | 12 4 4. z在第三象限, 因此
得知线段
z1 z2
的中点为
例3 求下列方程所表示的曲线:
z1 z2 z 2
1) 2) 3)
| z i | 2; | z 2i || z 2 |; Im(i z ) 4.
[解]：1)
| z i | 2
y x i
设 z = x + i y , 方程变为
| x ( y 1)i | 2 x ( y 1) 2,
1 2 1 2 1 2 2 1 1 2
z xx yy x y xy i ( z 0) z x x x x
1 1 2 2 1 2 2 2 1 2 1 2 2 2 2 1 2 1 2
复数运算满足交换律,结合律和分配律:
z1+z2=z2+z1 ; z1z2=z2z1 ; z1+(z2+z3)=(z1+z2)+z3 z1(z2z3)=(z1z2)z3 ; z1(z2+z3)=z1z2+z1z3

复数的乘幂与方根

复数的乘幂与方根

8 2(cos 4 4
i sin 4 4
)
(k 0,1, 2, 3)
解：将向量
z1
z2逆时针旋转


3
后得到的向量
z1
z3
学
或z1z3的终点即为所求.
复 变 函 数


z3

z1

(cos
3

i sin
3
)( z2
y
z1
)
与 积 分
( 1 i 3 )(1 i)
变 换
22
13 13
z3 z2

3 z2 z1
( ) ( )i
22 22
复
1 4
4
变 函 数
w2 r n (cos n i sin n )
与
积 分 变 换
wn1

1
r n (cos

2(n 1)
n


i sin
2(n 1)
n
)
而k取其它整数时，这些根又会重复出现。
哈
例1 求 3 1
尔
滨
工
程
大
学
例2 设z 1 i,求z4和4 z
z1
x
哈 尔
所以
z3

3 ( 2

31 )(
22
3 )i
2
滨 工 程
同理，若转角为 ，可得
大 学
3
y
复 变 函
z3

(3 2

3)(1 22
3 )i 2
数
与
积
分

复变函数与积分变换-01-03

复变函数与积分变换-01-03

r
1 n
cos
2(n n
1)π
i
sin
2(n n
1)π
.
当k以其他整数值代入时, 这些根又重复出现.
13
例如 k n时,
wn
r
1 n
cos
2nπ n
i sin
2nπ n
r
1 n
cos
n
i
sin
n
w0
.
从几何上看, n z 的 n 个值就是以原点为中心,
1
r n 为半径的圆的内接正 n 边形的 n 个顶点.
2kπ n
(k 0,1,2,,n 1)
推导过程如下:
11
设 z r(cos i sin ), w (cos i sin ),
根据棣莫佛公式,
wn n(cosn i sin n ) r(cos i sin ),
于是 n r, cosn cos , sin n sin ,
旋转
3
(或
3
)就得
y
z3
3
o z1 1
z2 2 i
x
z3
到另一个向量, 它的终点即为所求顶点z3 (或 z3 ).
因
为复
数
e
i 3
的模为1,
转角
为
,
3
8
i
z3 z1 e 3 (z2 z1 ) 1 3 i (1 i)
2 2 1 3 1 3 i
2 2 2 2
4
设复数z1和z2的指数形式分别为 z1 r1ei1 , z2 r2ei2 , 则 z1 z2 r1 r2ei(12 ) .
由此可将结论推广到 n 个复数相乘的情况:

复变函数与积分变换重要知识点归纳

复变函数与积分变换重要知识点归纳

复变函数复习重点(一)复数的概念1.复数的概念：z x iy =+，,x y 是实数,()()Re ,Im x z y z ==.21i =-. 注：一般两个复数不比较大小，但其模（为实数）有大小.2.复数的表示1）模：22zx y =+；2）幅角：在0z ≠时，矢量与x 轴正向的夹角，记为()Arg z （多值函数）；主值()arg z 是位于(,]ππ-中的幅角。

3）()arg z 与arctan y x之间的关系如下：当0,x >arg arctan y z x=；当0,arg arctan 0,0,arg arctan yy z x x y y z xππ⎧≥=+⎪⎪<⎨⎪<=-⎪⎩； 4）三角表示：()cos sin z z i θθ=+，其中arg z θ=；注：中间一定是“+”号。

5）指数表示：i z z e θ=，其中arg z θ=。

(二)复数的运算1.加减法：若111222,z x iy z x iy =+=+，则()()121212z z x x i y y ±=±+±2.乘除法：1）若111222,z x iy z x iy =+=+，则()()1212122112z z x x y y i x y x y =-++；()()()()112211112121221222222222222222x iy x iy z x iy x x y y y x y x i z x iy x iy x iy x y x y +-++-===+++-++。

2）若121122,i i z z e z z e θθ==,则()121212i z z z z e θθ+=；()121122i z z ez z θθ-=3.乘幂与方根1） 若(cos sin )i z z i z e θθθ=+=，则(cos sin )nnn in z z n i n z e θθθ=+=。

1复数概念2表示法3乘幂与方根4区域

1复数概念2表示法3乘幂与方根4区域

把其中满足 0 的θ0称为辐角Argz的主值，
记作θ0=argz。 z=0时，辐角不确定。
计算 argz(z≠0)



arg
z


arctan 2
y x
x 0, y R
x 0, y 0
的公式
arctan
y x

x 0, y 0
3i 2
的模 ,辐角及辐.角主值
例 4 .求 (1 )e2 i(2 )3 e i(3 )e 2 的 ,辐 模 . 角
例5. 将zsinicos化为三角形式 式.与
5
5
§3 复数的乘幂与方根
1. 复数的乘积与商 2. 复数的乘幂 3.复数的方根
1. 乘积与商
定理1 两个复数乘积的模等于它们的模相乘， 两个复数乘积的辐角等于它们的辐角相加。
z n

1 zn
.
由定义 zn得 rnein
3.复数的方根（开方）——乘方的逆运算
问题 给定复数z=re i ，求所有的满足ωn=z 的
复数ω。
当z≠0时，有n个不同的ω值与 n 相z 对应，每一
个这样的ω值都称为z 的n次方根，记 n z
设ei,由 nz,有nein re i
•复数z 的实部 Re(z) = x ; 虚部 Im(z) = y . (real part) (imaginary part)
• 复数的模 |z| x2y2 0 • 判断复数相等 z 1 z 2 x 1 x 2 ,y 1 y 2 ,其 z 1 中 x 1 i1 y ,z 2 x 2 i2 y z 0 R z) eI(m z) 0(
1. 点的表示

复变函数与积分变换重要知识点归纳

复变函数与积分变换重要知识点归纳

复变函数复习重点(一)复数的概念1.复数的概念：z x iy =+，,x y 是实数,()()Re ,Im x z y z ==.21i =-.注：一般两个复数不比较大小，但其模（为实数）有大小. 2.复数的表示1）模：z=2）幅角：在0z ≠时，矢量与x 轴正向的夹角，记为()Arg z （多值函数）；主值()arg z 是位于(,]ππ-中的幅角。

3）()arg z 与arctan y x之间的关系如下：当0,x > arg arctanyz x=；当0,arg arctan 0,0,arg arctan yy z x x y y z xππ⎧≥=+⎪⎪<⎨⎪<=-⎪⎩； 4）三角表示：()cos sin z z i θθ=+，其中arg z θ=；注：中间一定是“+”号。

5）指数表示：i z z e θ=，其中arg z θ=。

(二) 复数的运算1.加减法：若111222,z x iy z x iy =+=+，则()()121212z z x x i y y ±=±+±2.乘除法：1）若111222,z x iy z x iy =+=+，则()()1212122112z z x x y y i x y x y =-++；()()()()112211112121221222222222222222x iy x iy z x iy x x y y y x y x i z x iy x iy x iy x y x y +-++-===+++-++。

2）若121122,i i z z e z z e θθ==, 则()121212i z z z z eθθ+=；()121122i z z e z z θθ-=3.乘幂与方根1） 若(cos sin )i z z i z e θθθ=+=，则(cos sin )nnn in z z n i n z e θθθ=+=。

复变函数与积分变换1.3复数的乘幂与方根

复变函数与积分变换1.3复数的乘幂与方根
2 2 2
所以
z1 z 2 z 3 z1 z 2 z 2 z 3 z 3 z1 0 .
2 2 2
二、 乘方与开方运算（幂与根 ） 1）乘方
z r e
n n
in
r
n
co s n
i sin n

令|z|=1,则得到 德莫佛(De Moivre) 公式：
co s
3
i sin

n
co s n i sin n
2 ）开方:
若满足 w
n
z
记为
则称w为z的n次方根, 于是
w
iArg z
n
z .
w e
n
inArg w
ze
推得
w n z a rg z 2 k A rg w n ( k 0,1, 2, , n 1)
例2 求
4
1 i.
2 co s i sin , 4 4
[解] 因为
1 i
所以
2 k 2 k 2 cos 4 i sin 4 4 4
, ( k 0,1, 2, 3)
4
1 i
8
w1
2
w0 x
w2
O
8
8
w3
四个根是内接于中心在原点半径为21/8的圆的正方形 的四个顶点.
例3 求
3
8.
解 因为 8 8 (cos i sin )， 所以
3
8
3
8 (cos
2 k
3
i sin i sin
2 k

(完整word版)1.3复数的乘幂与方根

(完整word版)1.3复数的乘幂与方根

1.3复数的乘幂与方根一、乘积与商定理一.两个复数乘积的模等于它们的模相乘，两个复数乘积的辐角等于它们的辐角相加：1212z z z z ⋅=；1212rg()rg()rg()A z z A z A z =+或者12()1212i z z r r e θθ+=。

注：定理中1212rg()rg()rg()A z z A z A z =+两边是角的集合相等。

证明：令1111(cos sin )z r i θθ=+，2222(cos sin )z r i θθ=+12121122(cos sin )(cos sin )z z r r i i θθθθ⋅=⋅++1212121212[(cos cos sin sin )(sin cos cos sin )]r r i θθθθθθθθ=⋅-++ 121212[cos()sin()]r r i θθθθ=⋅+++几何意义：将复数1z 按逆时针方向旋转一个 角度2()Arg z 再将其伸缩到2z 倍。

令1z i =+由复数乘法的几何意义说明下列 复数如何生产：1.(1z +；2.(1z -；3.(1)z i -如何得到下列复数：1. 将z 逆时针旋转120度，模扩大三倍2. 将z 顺时针旋转120定理二.两个复数的商的模等于它们的模的商，两个复数的商的辐角等于被除数与除数的辐角之差。

即：2211z z z z =；2211rg()rg()rg()z A A z A z z =-注：定理中2211rg()rg()rg()z A A z A z z =-两边是角的集合相等。

证明：由除法定义21z z z =，即：21z zz =。

由定理一得：11z z z z ⋅=；11rg()rg()rg()A zz A z A z =+2211z z z z ∴=；2211rg()rg()rg()z A A z A z z =-定理一和定理二如果用复数的指数形式证明则更简单。

复变函数复习要点

复变函数复习要点

轴
轴 轴 轴
4
2.复变函数——映射
w f ( z ) u( x , y ) iv ( x , y )
u u( x , y ) v v ( x , y )
例3 求下列方程所表示的曲线: (1) z i 2; i z ) 4.
复变函数与积分变换 复习概要
1.复数的运算
加减乘除 共轭 乘幂 方根
zz z
2
复数的三角表示式： 1）模和幅角的定义 z x iy 习惯上把表示式 称为复数的直角坐标表 三 示式或代数形式，利用直角坐标系和极坐标之间的 角 x r cos y r sin 表 联系 则 示
0
7.由调和函数确定解析函数
已知一个调和函数 u (v), 求调和函数 v( u), 使得u+vi是一个解析函数. 偏积分法 凑微分法 曲线积分法
dv v x dx v y dy u y dx ux dy .
不定积分法
f ( z ) ux iu y U ( z ) f ( z ) U ( z )dz ,
10
如果将 Lnz ln z iArgz 中 Argz 取主值arg z ,
那末 Lnz 为一单值函数， 记为 ln z， 称为 Lnz 的主值.
ln z ln z i arg z .
其余各值为 Lnz ln z 2ki ( k 1,2,),
对于每一个固定的k , 上式确定一个单值函数 , 称为 Lnz 的一个分支.
C2 Cn
常用参数方程形式
z (1 t )z1 tz2
0 t 1
(b)圆周
z z0 re
i
0 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
, ( k 0,1, 2, 3)
4
1 i
8
w1
即
w0 w1 w2 w3
8
y
1+i
2 co s i sin 16 16
,
2
8
8
9 9 2 co s i sin , 16 16 1 7 1 7 2 co s i sin , 16 16 2 5 2 5 2 co s i sin . 16 16
当 k 0 时， 0 2 (cos

3

3
) 1 3i ，
当 k 1 时， 1 2 (cos i sin ) 2 ， 当 k 2 时， 2 2 (cos
5 3 i sin 5 3
3
) 1 3i
我们知道，在实数域内， 8 只有一个值 2 ，而在复数域内， 8 有三个根，且它们是内接于中心在 原点，半径为 2 的圆的正三角形的三个顶点
即
z 3 z1 z 3 z 2 z 3 z1 z 2 z1 z 2 z1 z 2 z1 z 2 ，
2 2 2
所以
z1 z 2 z 3 z1 z 2 z 2 z 3 z 3 z1 0 .
2 2 2
二、 乘方与开方运算（幂与根 ） 1）乘方
z r e
无限集合, 两边的集合相等, 即每给定等式左边的一个
数, 就有等式右边的一个数与之对应, 反之亦然.
例：设 z1 1 ,
z 2 i . 则： z z i e 1 2
i

2
;
A rgz1 2 n ,
A rg z 2

2
2
2 m ,
2k
A r g z1 z 2 A r g z1 A r g z 2
2
定理1 两个复数乘积的模等于它们的模的乘积, 两个复 数乘积的幅角等于它们幅角的和.
y
z1 z 2
r1 r2
r2
乘法的几何意义: 几何上 z1z2 相当 于将 z2 的模扩 大 |z1| 倍并旋转
iz1
1 2
1
z2
z1
2 z1
1
2
r1
一个角度Arg z1 .
0
1
x
等式 Arg(z1z2)=Arg z1+Arg z2的意思是等式的两边都是
2
w0 x
w2
O
8
8
w3
四个根是内接于中心在原点半径为21/8的圆的正方形 的四个顶点.
例3 求
3
8.
解 因为 8 8 (cos i sin )， 所以
3
8
3
8 (cos
2 k
3
i sin i sin
2 k
3
) ( k 0，， ) . 1 2
n n
in
r
n
co s n
i sin n

令|z|=1,则得到 德莫佛(De Moivre) 公式：
co s
i sin

n
co s n i sin n
2 ）开方:
若满足 w
n
z
记为
则称w为z的n次方根, 于是
w
iArg z
n
z .
w e
n
inArg w
§1.3 复数的乘幂与方根
一、乘积与商
z 1 r1 e
i 1
z 2 r2 e
i 2
z1 z 2 r1 r2 e
i ( 1 2 )
| z 1 z 2 | r1 r2 | z 1 || z 2 | Arg ( z 1 z 2 ) Argz 1 Argz
3


3
后得到的向量 z 1 z 3 或 z 1 z 3 的终点 z 3 或 z 3 即
为所求. 根据复数的乘法，有
z 3 z 1 (cos

3
i sin

3
)( z 2 z 1 )
1 3 ( i )( 1 i ) 2 2
1 3 1 3 ( )( )i ， 2 2 2 2

则有
即
3 2
k,m ,n Z

2

2 ( m n )
2 k ,
k=m+n+1
按照乘积的定义, 当z10时, 有
z2 z2 z1 z2 z1 z2 z1 z1 z2 A rgz2 A rg A r g z1 z1
z1
证
如图，向量 z

1
z2
旋转 得到向量 z
3

1
z3
，向量 z
2
z3
旋转 得到向量 z
3

2
z1
，由于复数 e 的模为 1，
3
i

辐角为 .( z 2 z 1 )， z 1 z 2 e 3 ( z 3 z 2 ) ，
i

i

由此得
z 3 z 1 ( z 3 z 2 ) ( z 2 z 1 )( z 1 z 2 ) .
所以
3 3 1 3 z3 ( )( )i . 2 2 2 2
同理，若转角为 ，可得
3
3 3 1 3 z3 ( ＋ )( － )i 2 2 2 2

例2
设复数 z ，z ，z 对应等边三角形的三个顶点，证明：
1 2 3
2 2 2 z1 z 2 z 3 z1 z 2 z 2 z 3 z 3 z1 0 .
3
0

z2 z2 z1 z1 z2 A rg A r g z 2 A r g z1 z1
z2
;

r2 r1
e
i ( 2 1 )
z1
定理2 两个复数的商的模等于它们的模的商, 两个复数 的商的辐角等于被除数与除数的幅角之差.
解
如图，将向量 z 1 z 2 逆时针旋转 或
ze
推得
w n z a rg z 2 k A rg w n ( k 0,1, 2, , n 1)
从而
n
z
1
i n
arg z 2 k n
z
e
r
n
arg z 2 k arg z 2 k i sin cos n n
( k 0,1, , n 1)
几何解释：z1/n的n个值就是以原点为中心, r1/n为半径 的圆的内接正n边形的n个顶点。
例2 求
4
1 i.
2 co s i sin , 4 4
[解] 因为
1 i
所以
2 k 2 k 2 cos 4 i sin 4 4 4