地下洞室围岩应力与围岩压力计算
- 格式:doc
- 大小:16.61 MB
- 文档页数:28

隧道开挖应力理论分析发布时间:2021-10-27T02:52:17.598Z 来源:《基层建设》2021年第20期作者:张旭[导读] 摘要:通过理论对隧道的掌子面开挖后的应力状态进行了分析,通过强度劣化理论对其进行仰拱施工过程的理论分析。
身份证:21092219930715XXXX摘要:通过理论对隧道的掌子面开挖后的应力状态进行了分析,通过强度劣化理论对其进行仰拱施工过程的理论分析。
目前,隧道理论分析相对比较成熟,为国家交通事业提供了强大的后盾。
关键词:隧道;应力分析;掌子面;仰拱引言隧道经过多年发展,形成了一个完整的体系,已经包含勘察、设计、施工、监测、检测、科研、理论等方面。
而隧道的应力分析,无论是对设计、施工等各阶段都起到了非常重要的理论支撑作用。
因此,对于隧道的应力分析有着极为重要的意义。
1地下硐室应力分析地下硐室主要分为隧道、井巷、地下水电站厂房等一系列地下工程,随着科技的发展,矿山采选一体化理念被提出来,地下硐室又增加了地下厂房的工程。
如何获得地下硐室围岩应力,就掌握着地下工程的稳定性。
应力分析理论大部分都近似圆形进行分析,而隧道断面更加接近圆形,更加符合圆形理论,例如经典的地下硐室围岩应力理论。
当隧道还未形成时,隧道还处于原始情况,为了对其方便分析,假设周围力相同,周围的岩体处于弹性状态。
因此,其竖向应力可以表示为:式中:σ——岩体垂直应力,MPa;γ——岩体重度,kN/m;H——岩体埋深,m。
当断面形成以后,重新形成新的应力状态,在断面附近也会出现新的应力集中的现象的,如果此时的应力超过了岩体自身的强度,岩体就会进入塑性状态,逐渐向不稳定状态发展。
根据弹性力学的极限平衡理论,在静水压力下,围岩的应力和变形如下式所示:极限平衡半径:式中:P——静水压力,MPa;Pi——支护阻力,MPa;r0——圆形巷道半径,m;r——所求应力处半径,m;——围岩的内摩檫角,°;G——剪切模量,MPa。

洞顶位移底鼓在岩石地下工程中,受开应力状态发生改二、地下洞室开挖所产生的岩体力学问题向新的平衡应力状态调整,应力状态的调整过程,称(redistribution of stress)。
洞顶位移底鼓由于洞径方向的变形远大于洞轴方向的变形,当洞室半径远小于洞长时,洞轴方向的变形可以忽略不计,因此地下洞室问题可视为平面应变问题深埋于弹性岩体中的水平圆形洞室,其围岩重分布应力按柯西课题求解(1)柯西课题概化模型无限大弹性薄板,其边界上受到沿方向的外力作用,薄板中有一半径为的小圆孔。
x p R 弹性薄板柯西课题分析示意图pp 1.深埋圆形水平洞室围岩重分布应力以圆的圆心为原点取极坐标,由弹性理论,若不考虑体积力,可求得薄板中任一点的应力及其方向。
(,)M r θ弹性薄板柯西课题分析示意图p p若应力函数为φ22211r r r r φφσθ∂∂=+∂∂径向应力:22rθφσ∂=∂环向应力:2211r r r r θφφτθθ∂∂=−∂∂∂剪切应力:(2)柯西课题解弹性薄板柯西课题分析示意图p p边界条件:()cos 222r r b p pσθ==+()sin 22r r b pθτθ==−0b R >>()()0r r r b r b θτσ====0b R =0b R >>vσxθMvσ0R r弹性薄板pp柯西课题力学模型中极坐标轴与力的作用方向相同。
因此,需进行极角变换。
2420002423411cos22v r R R R r r r σσθ⎡⎤⎛⎞⎛⎞=−−+−⎢⎥⎜⎟⎜⎟⎝⎠⎝⎠⎣⎦240024311cos22v R R r r θσσθ⎡⎤⎛⎞⎛⎞=+++⎢⎥⎜⎟⎜⎟⎝⎠⎝⎠⎣⎦420042321sin22v r R R rr θστθ⎛⎞=−+⎜⎟⎝⎠2)由柯西课题解得到作用下圆形洞室围岩重分布应力v σ22θθπ→−2θσσ=④随着距离增大,增大,减小,并且都逐渐趋近于天然应力。

深埋隧道围岩压力计算例题及解析下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!1. 引言在地下工程设计中,深埋隧道的围岩压力计算是至关重要的一步。


先说Kv值的计算,Kv值指围岩的完整性系数,是表现围岩完整性的定量指标之一。
Kv=(Vpm/Vpr)^2,其中Vpm是岩体内的弹性波速,Vpr是岩石的弹性波速。
围岩越完整,岩体内裂隙越少,其比值约接近1。
这个值还真得要通过对代表性的点或段进行声波测试才能得出。
就目前国内计算围岩压力的方法,是将坑道开挖的松弛围岩质量作为荷载加在支护结构上。
但松弛荷载的几种计算方法,一种是经验公式,是根据单线铁路施工塌方的统计资料得到的经验公式,目前铁路、公路的隧道设计规范仍沿用了这个公式。
另外是基于太沙基或普氏理论的出的公式。
具体可以查阅《公路隧道设计规范》《铁路隧道设计规范》。
由于围岩压力计算跟具体的洞室形状、施工方法、时间效应等相关度太大,规范中的计算参数过于经验化,应该来说客观性比较缺乏。
比如根据塌方的到的经验公式,其针对的情况是跨度5-10m的马蹄形断面,就目前动辄15m以上的跨度,扁平率较大的隧道而言,取值是不甚合理的。
而通过有限元的方法计算,还有一些计算公式,但计算的前提大部分是假定围岩是理想弹塑性介质,与实际的岩土材料应力-应变性质不尽相同。
尤其对于破裂的岩体而言,问题更为突出。
而就大多数需要计算的地下结构而言,往往是处于软岩或破碎岩体之中。
比较能反应实际隧道压力情况情况的办法当然是通过直接测定,但无论是通过压力盒直接测定或形变间接推算或通过监控信息进行反演计算,都还比较困难。
对于围岩松动圈的具体测定我个人比较认可通过钻孔进行超声波探测。
就个人经验而已,双车道隧道的松弛半径大概在1.5倍的开挖洞径,围岩荷载按0.5-1倍洞径计算比较合适。

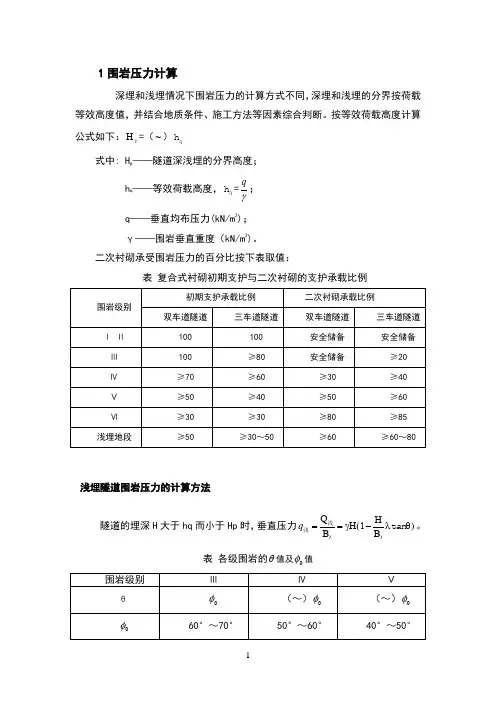
1围岩压力计算深埋和浅埋情况下围岩压力的计算方式不同,深埋和浅埋的分界按荷载等效高度值,并结合地质条件、施工方法等因素综合判断。
按等效荷载高度计算公式如下:HP =(~)qh式中: Hp——隧道深浅埋的分界高度;hq ——等效荷载高度,qh=qγ;q——垂直均布压力(kN/m2);γ——围岩垂直重度(kN/m3)。
二次衬砌承受围岩压力的百分比按下表取值:表复合式衬砌初期支护与二次衬砌的支护承载比例浅埋隧道围岩压力的计算方法隧道的埋深H大于hq而小于Hp时,垂直压力QB Bt tqH==γH(1-λθ)浅浅tan。
表各级围岩的θ值及φ值2(tan 1)tan tan tan c cc ϕ+ϕβϕ+ϕ-θc tan =tan侧压力系数()tan tan tan tan tan tan tan tan cc c β-ϕλ=β1+βϕ-θ+ϕθ⎡⎤⎣⎦作用在支护结构两侧的水平侧压力为:e 1=γh λ ; e 2=γ(h+Ht)λ 侧压力视为均布压力时:Ⅴ级围岩的等效荷载高度hq=×24×[1+×(10-5)]= Hp==27m,H<Hq,故为浅埋。
取φ0=45°,θ=φ0=27°,h=20m ,tan β=,λ=,tan θ=, 计算简图:()212+1e =e e垂直压力q=19×20×20×10)=mPg=πdγ=π××25=m地基反力P=me1=γhλ=19×20×=e2=γ(h+Ht)λ=19×(20+×=水平均布松动压力e=(e1+e2)/2=mⅤ级围岩二衬按承受50%围岩压力进行计算,则垂直压力为q×50%=m地基反力为P×50%=m水平压力为e×50%=m2衬砌结构内力计算表等效节点荷载表轴力、剪力、弯矩详细数据50+0557********51+05409972930652+05240502556953+052115954+0517015内力图分析(1)轴力:由ANSYS建模分析围岩衬砌内力得出轴力图如图,最大轴力出现在仰拱段,其值为。

1围岩压力计算1围岩压力计算深埋和浅埋情况下围岩压力的计算方式不同,深埋和浅埋的分界按荷载等效高度值,并结合地质条件、施工方法等因素综合判断。
按等效荷载高度计算公式如下:HP =(2~2.5)qh式中: Hp——隧道深浅埋的分界高度;hq ——等效荷载高度,qh=qγ;q——垂直均布压力(kN/m2);γ——围岩垂直重度(kN/m3)。
二次衬砌承受围岩压力的百分比按下表取值:表4.1 复合式衬砌初期支护与二次衬砌的支护承载比例围岩级别初期支护承载比例二次衬砌承载比例双车道隧道三车道隧道双车道隧道三车道隧道ⅠⅡ100 100 安全储备安全储备Ⅲ100 ≥80 安全储备≥20 Ⅳ≥70 ≥60 ≥30 ≥40 Ⅴ≥50 ≥40 ≥50 ≥60 Ⅵ≥30 ≥30 ≥80 ≥85浅埋地段≥50 ≥30~50≥60 ≥60~801.1 浅埋隧道围岩压力的计算方法隧道的埋深H 大于hq 而小于Hp 时,垂直压力Q B B t tq H==γH(1-λθ)浅浅tan 。
表4.3 各级围岩的θ值及0φ值围岩级别Ⅲ ⅣⅤθ0.90φ (0.7~0.9)0φ (0.5~0.7)0φ 0φ60°~70°50°~60°40°~50°2(tan 1)tan tan tan c cc ϕ+ϕβϕ+ϕ-θc tan =tan 侧压力系数()tan tan tan tan tan tan tan tan cc c β-ϕλ=β1+βϕ-θ+ϕθ⎡⎤⎣⎦作用在支护结构两侧的水平侧压力为:e 1=γh λ ; e 2=γ(h+Ht)λ 侧压力视为均布压力时:Ⅴ级围岩的等效荷载高度hq=0.45×24×[1+0.1×(10-5)]=10.8m Hp=2.5hq=27m,H<Hq,故为浅埋。
取φ0=45°,θ=0.6φ0=27°,h=20m ,tan β=3.02,λ=0.224,tan θ=0.51, 计算简图:()212+1e =e e3 2072.757146 1543.972843 26425.97397 4953.6865524 2072.800753 1543.507634 26256.11233 9886.1615315 2072.873244 1543.046044 25973.81825 14776.30132 2 2072.974338 1542.589864 24195.36508 23664.97654 7 2073.219875 1542.146273 20103.90754 40260.144586 2073.651412 1541.88012 14076.90744 57497.450139 2074.154041 1541.73685 8935.043764 69728.9710410 2074.661668 1541.61244 6853.524396 83279.0729311 2075.173585 1541.507065 5880.169138 84021.8174612 2075.689079 1541.42087 4898.834757 84650.5451413 2076.20743 1541.353977 3910.852859 85164.4039714 2076.727917 1541.306479 2917.564275 85562.6960915 2077.249814 1541.27844 1920.316498 85844.8859416 2077.772394 1541.269902 920.4626612 86010.5840317 2078.294929 1541.280875 80.64000409 86059.5712718 2078.81669 1541.311344 -1081.63324 85991.7746219 2079.33695 1541.361267 -2081.158789 85807.2914620 2079.854984 1541.430575 -3077.860187 85506.3814621 2080.37007 1541.51917 -4070.385072 85089.4259922 2080.88149 1541.626929 -5057.386718 84557.009323 2081.388532 1541.753702 -6037.525576 83909.86178 2081.890488 1541.899313 -7009.471578 83148.84332 25 2082.285648 1542.168245 -9244.515303 74199.42618 24 2082.510844 1542.589864 -14047.47015 52646.5891327 2082.611937 1543.046044 -19236.06506 36865.6479128 2082.684429 1543.507634 -23588.83673 22476.6373729 2082.728036 1543.972843 -25973.81825 14776.30132 26 2082.742591 1544.439864 -26256.11233 9886.16153130 2082.706135 1545.042547 -26425.97397 4953.68655231 2082.5973 1545.636442 -31304.66167 2146.31214432 2082.417672 1546.212888 -35817.57933 -13486.3166533 2082.169871 1546.76348 -34895.66231 -26741.8859834 2081.85751 1547.280188 -33376.67067 -39539.8892835 2081.485145 1547.755477 -31286.59479 -51661.3504136 2081.058204 1548.182418 -28661.19683 -62898.8811837 2080.582915 1548.554783 -25545.39795 -73060.1921438 2080.066207 1548.867144 -21992.50975 -81971.412939 2079.515615 1549.114945 -18063.32375 -89480.0825240 2078.939169 1549.294573 -13825.06958 -95457.7295441 2078.345274 1549.403408 -9350.264619 -99802.0707842 2077.742591 1549.439864 -4715.473839 -102438.770543 2077.139908 1549.403408 0 -103322.708244 2076.546013 1549.294573 4715.473839 -102438.763145 2075.969566 1549.114945 9350.264619 -99802.0707846 2075.418975 1548.867144 13825.06984 -95457.7368747 2074.902267 1548.554783 18063.324 -89480.0898548 2074.426978 1548.182418 21992.50975 -81971.412949 2074.000037 1547.755477 25545.39769 -73060.1848150 2073.627672 1547.280188 28661.19683 -62898.8811851 2073.315311 1546.76348 31286.59505 -51661.3504152 2073.06751 1546.212888 33376.67067 -39539.8819553 2072.887882 1545.636442 34895.66205 -26741.8859854 2072.779047 1545.042547 35817.57908 -13486.32398表4.8 轴力、剪力、弯矩详细数据节点号轴力弯矩剪力1 -8.92E+05 -13456 -109952 -8.83E+05 -8352.6 -638913 -8.73E+05 21398 -1.19E+054 -8.61E+05 76686 -1.72E+055 -8.69E+05 1.57E+05 -252076 -7.80E+05 1.69E+05 3.16E+057 -2.08E+06 7906.2 339838 -2.06E+06 -11168 325749 -2.05E+06 -29519 2963810 -2.04E+06 -46347 2539511 -2.03E+06 -60967 2007312 -2.02E+06 -72813 1390913 -2.02E+06 -81442 7144.714 -2.02E+06 -86540 26.68815 -2.02E+06 -87920 -7193.616 -2.02E+06 -85526 -1426717 -2.02E+06 -79433 -2094718 -2.03E+06 -69844 -2698819 -2.04E+06 -57093 -3214820 -2.05E+06 -41637 -3619121 -2.07E+06 -24058 -3889122 -2.08E+06 -5056.4 -4002923 -7.88E+05 14553 -3.07E+0524 -8.72E+05 1.60E+05 1869325 -8.67E+05 1.51E+05 1.61E+0526 -8.78E+05 75321 1.12E+0527 -8.89E+05 22802 6085928 -8.97E+05 -5736 1042929 -9.06E+05 -10643 -1582730 -9.04E+05 -976.56 -1884631 -8.96E+05 10731 -2262932 -8.82E+05 24936 -2597333 -8.61E+05 41366 -2494434 -8.33E+05 57370 -1258435 -7.99E+05 66092 2076436 -7.60E+05 54844 4538037 -7.22E+05 28879 5781438 -6.87E+05 -4468.5 5896639 -6.58E+05 -38409 5047240 -6.38E+05 -67143 3459441 -6.27E+05 -86237 1407042 -6.26E+05 -92913 -8065.143 -6.37E+05 -86224 -2867644 -6.57E+05 -67117 -4472845 -6.85E+05 -38371 -5348046 -7.19E+05 -4418.2 -5266647 -7.57E+05 28940 -4064448 -7.94E+05 54916 -1651049 -8.29E+05 66173 1653250 -8.56E+05 57316 2859051 -8.76E+05 40997 2930652 -8.90E+05 24050 2556953 -8.98E+05 9154.2 2115954 -8.99E+05 -3292.6 17015内力图分析(1)轴力:由ANSYS建模分析围岩衬砌内力得出轴力图如图,最大轴力出现在仰拱段,其值为626.383kN。

第一节概述1.地下洞室(underground cavity):指人工开挖或天然存在于岩土体中作为各种用途的构筑物。
2.我国古代的采矿巷道,埋深60m,距今约3000年左右(西周)。
目前,地下洞室的最大埋深已达2500m,跨度已过50m,同时还出现有群洞。
3.分类:按作用分类:交通隧洞(道)、水工隧洞、矿山巷道、地下厂房仓库、地铁等等;按内壁有无水压力:有压洞室和无压洞室;按断面形状为:圆形、矩形或门洞形和马蹄形洞室等;按洞轴线与水平面间的关系分为:水平洞室、竖井和倾斜洞室三类;按介质,土洞和岩洞。
4.地下洞室→引发的岩体力学问题过程:地下开挖→天然应力失衡,应力重分布→洞室围岩变形和破坏→洞室的稳定性问题→初砌支护:围岩压力、围岩抗力(有内压时)(洞室的稳定性问题主要研究围岩重分布应力与围岩强度间的相对关系)第二节围岩重分布应力计算1.围岩:指由于人工开挖使岩体的应力状态发生了变化,而这部分被改变了应力状态的岩体。
2.地下洞室围岩应力计算问题可归纳的三个方面:①开挖前岩体天然应力状态(一次应力、初始应力和地应力)的确定;②开挖后围岩重分布应力(二次应力)的计算;③支护衬砌后围岩应力状态的改善。
3.围岩的重分布应力状态(二次应力状态):指经开挖后岩体在无支护条件下,岩体经应力调整后的应力状态。
一、无压洞室围岩重分布应力计算1.弹性围岩重分布应力坚硬致密的块状岩体,当天然应力,地下洞室开挖后围岩将呈弹性变形状态。
这类围岩可近似视为各向同性、连续、均质的线弹性体,其围岩重分布应力可用弹性力学方法计算。
重点讨论圆形洞室。
(1)圆形洞室深埋于弹性岩体中的水平圆形洞室,可以用柯西求解,看作平面应变问题处理。
无限大弹性薄板,沿X方向的外力为P,半径为R0的小圆孔,如图8.1所示。
任取一点M(r,θ)按平面问题处理,不计体力。
则:图8.1柯西课题分析示意图……………………①式中为应力函数,它是和的函数,也是和的函数。


隧道围岩分级及围岩压力隧道所穿过的地层是千变方化的,可能遇到各种工程性质不同的围岩。
隧道围岩分级是评价隧道围岩稳定性的重要参数,也是隧道支护方案设计和施工工艺确定的主要依据。
分级的正确与否直接影响着隧道施工和运营安全,因此,正确划分隧道围岩分级就显得尤为重要。
在围岩分级确定的情况下,如何确定支护结构上的作用力(即围岩压力)就成为正确、合理设计隧道结构的关键。
4.1 围岩岩性与初始应力4.1.1 围岩岩性隧道工程围岩是指地壳中受开挖活动影响的那一部分岩土体。
这个范围在横断面上约为6~10倍的洞径。
围岩的工程性质,一般包括三个方面:物理性质、水理性质和力学性质。
而对围岩稳定性最有影响的是力学性质,即围岩抵抗变形和破坏的性能。
围岩既可以是岩体,也可以是土体。
本书仅涉及岩体的力学性质。
岩体是在漫长的地质历史中形成的地质体,被许许多多不同方向、不同规模的断层面、层理面、节理面和裂隙面等各种地质界面切割为大小不等、形状各异的各种块体。
这些地质界面称为结构面或不连续面,这些块体称为结构体,岩体可以看作由结构面和结构体组合而成的具有结构特征的地质体。
所以,岩体的力学性质主要取决于岩体的结构特征、结构体岩石的特性及结构面的特性。
环境因素,尤其地下水和地应力对岩体的力学性质影响也很大。
在软弱围岩中,节理和裂隙比较发育,岩体被切割破碎,结构面对岩体的变形和破坏都不起主导作用,所以岩体的特性与结构体岩石的特性并无本质区别。
在完整而连续的岩体中亦是如此。
反之,在坚硬的块状岩体中,由于受软弱结构面切割,块体之间的联系减弱,此时,岩体的力学性质主要受结构面的性质及其在空间的组合所控制。
由此可见,岩体的力学性质必然是诸因素综合作用的结果。
岩体与岩石相比,两者有着很大的区别:与工程总体尺度相比,岩石几乎可以被认为是均质、连续和各向同性的介质;而岩体则具有明显的非均质性、不连续性和各向异性。
岩体抗拉变形能力差,因此,岩体受拉后很容易沿结构面发生断裂。
隧道围岩压力计算公式一、隧道围岩压力计算的基本原理地下隧道施工中,周围岩体对隧道的压力包括岩体重力及地表载荷对围岩的作用力两部分。
计算隧道围岩压力时需要考虑这两部分力的影响。
隧道围岩的重力即为岩体受重力作用的结果。
对于满足平衡条件的岩体,其重力可根据以下公式计算:G=γV其中,G为围岩重力,γ为围岩容重,V为岩体体积。
三、地表载荷计算公式地表载荷包括交通载荷、建筑物荷载等。
根据载荷的类型和特点,可以选取合适的计算公式进行计算。
例如,对于地面交通载荷,可以使用AASHTO公式、Burkill公式等进行计算。
根据隧道岩体的性质和周围环境的情况,可采用各种不同的计算公式。
下面列举几种常见的计算公式。
1. Culmann公式Culmann公式基于假设隧道周围岩体为弹性体,并假设岩体为各向同性的弹性体。
公式如下:P=2aγH/(√π)其中,P为围岩压力,a为自由差,γ为岩体容重,H为覆岩深度。
2. Moller公式Moller公式假设隧道周围岩体为半无限长的弹性体,该公式适用于围岩位于较深位置的隧道计算。
公式如下:P=(H/h)√πaγ其中,P为围岩压力,a为自由差,γ为岩体容重,H为覆岩深度,h 为地平面以上距离。
3.能量原理法能量原理法是根据岩体处于静力平衡状态时的能量等量原理得到的计算公式。
P = (2ah/V)∫(Fzdz)其中,P为围岩压力,a为自由差,V为岩体体积,F为岩体应力,z 为高度。
五、隧道围岩压力计算实例假设一个隧道,覆岩深度为H,岩体容重为γ,自由差为a。
根据Culmann公式,可计算出围岩压力:P=2aγH/(√π)六、综合考虑其他因素在实际工程中,还需要综合考虑其他因素,如地下水压力、地应力分布等。
这些因素会对计算结果产生一定的影响,需要在计算中进行相应的修正。
综上所述,隧道围岩压力计算涉及到地表载荷计算、岩体重力计算和计算公式的选择等多个方面。
在实际工程中,需要根据具体情况选取合适的计算公式,并综合考虑其他因素,以得到准确的围岩压力计算结果。
简析普氏理论求解洞室围岩压力问题作者:石喜梅来源:《科技与创新》2014年第17期摘要:地下开挖对周围地层的力学作用强度是随着距离的变化而逐渐衰减的。
深埋隧道上覆地层变形、松动、坍塌的过程会在地表以下某个相对稳定的范围内终止,就好像坍塌范围的周边出现了能够承受上覆岩层的“压力拱结构”一样,这种现象被称为地层的成拱作用。
此时,拱下坍落的重量决定了顶部的压力。
利用普氏理论求解塌落围岩压力。
关键词:普氏理论;地层;洞室围岩;压力中图分类号:TU457 文献标识码:A 文章编号:2095-6835(2014)17-0131-02该理论是由俄国学者普罗托季亚科诺夫提出的,其基本假定是:①岩体为没有黏聚力的松散体。
他认为,岩体中的结构面完全破坏了岩体的整体性,虽然岩体具有较弱的黏聚力,但是可以忽略;岩体抗拉、抗减、抗弯的能力极其微弱。
②深埋洞室开挖首先会引起洞顶塌落,但是这种塌落是有一定限度的,并在洞顶形成自然平衡拱。
1 普氏理论的受力分析机理普氏理论的受力分析不同于传统的受力分析,主要体现在三个方面:①自然拱的切线方向只作用有压应力,所以,它又被称为压力拱。
②压力拱以上岩体的重量(压力)通过压力拱传递到拱脚和附近岩体中,这可能会导致边墙被破坏。
所以,稳定的压力拱应该是考虑过边墙可能失稳范围后的最终压力拱。
③作用在衬砌上的压力就是压力拱与衬砌之间岩石的重量,与拱外岩体无关。
基于以上三点可知,问题的关键在于正确确定拱的形状。
当地质条件对称时,压力拱的受力和形状必然对称。
将压力拱(线)作为研究对象,把它当成对称问题研究。
取一半拱线分析,上端点受到轴向力Rx,下端点受水平和垂向力的作用(T,N),拱线受垂直和水平应力的作用,一般将水平应力计入拱座水平推力T中,忽略应力随着高度的变化而变化。
2 工程案例以某在建洞室为例,利用普氏理论对其进行围岩压力解析。
洞室的横断面如图1所示。
在图1中,某洞室建在普通的泥灰岩中,宽2a=8 m,高H=5 m。
第六章地下洞室围岩应力与围岩压力计算第一节概述一、地下洞室的定义与分类1、定义: 地下洞室(underground cavity)是指人工开挖或天然存在于岩土体中作为各种用途的地下空间。
2、地下洞室的分类按用途:矿山巷道(井)、交通隧道、水工隧道、地下厂房(仓库)、地下军事工程按洞壁受压情况:有压洞室、无压洞室按断面形状:圆形、矩形、城门洞形、椭圆形按与水平面关系:水平洞室、斜洞、垂直洞室(井)按介质类型:岩石洞室、土洞二、洞室围岩的力学问题(1)围岩应力重分布问题——计算重分布应力1)天然应力:人类工程活动之前存在于岩体中的应力。
又称地应力、初始应力、一次应力等。
2)重分布应力:由于工程活动改变了的岩体中的应力。
又称二次分布应力等。
地下开挖破坏了岩体天然应力的相对平衡状态,洞室周边岩体将向开挖空间松胀变形,使围岩中的应力产生重分布作用,形成新的应力状态,称为重分布应力状态。
(2)围岩变形与破坏问题——计算位移、确定破坏范围在重分布应力作用下,洞室围岩将向洞内变形位移。
如果围岩重分布应力超过了岩体的承受能力,围岩将产生破坏。
(3)围岩压力问题——计算围岩压力围岩变形破坏将给地下洞室的稳定性带来危害,因而,需对围岩进行支护、衬砌,变形破坏的围岩将对支衬结构施加一定的荷载,称为围岩压力(或称山岩压力、地压等)。
(4)有压洞室围岩抗力问题——计算围岩抗力在有压洞室中,作用有很高的内水压力,并通过衬砌或洞壁传递给围岩,这时围岩将产生一个反力,称为围岩抗力。
天然应力,没有工程活动 开挖洞室后的应立场,为重分布应力,与天然应力有所改变在附近开挖第二个洞室,则视前一个洞室开挖后的应力场为天然应力,第二个洞室开挖后的应力场为重分布应力第二节围岩重分布应力计算一、围岩重分布应力的概念围岩:洞室开挖后,应力重分布影响范围内的岩体。
围岩(重分布)应力:应力重分布影响范围内岩体的应力。
围岩应力与围岩性质、洞形、洞室受外力状态有关。
围岩应力计算包括以下步骤:①开挖前岩体天然应力状态的确定;②开挖后围岩重分布应力的计算 ;③支护衬砌后围岩应力状态的改善;围岩应力计算包括以下情形:弹性无压洞室围岩应力塑性无压洞室围岩应力有压洞室围岩应力二、无压洞室围岩应力计算1、弹性围岩应力围岩为坚硬致密的块状岩体,当天然应力大约等于或小于其单轴抗压强度的一半时,围岩呈弹性变形。
可近似视为各向同性、连续、均质的线弹性体(假设1),其围岩重分布应力可根据弹性力学计算。
(1)圆形洞室重分布应力的大小如果洞室半径相对洞长很小,按平面应变问题考虑(假设2),概化为受均布压力的薄板中心小圆孔周边应力分布的计算问题。
并忽略天然应力场沿洞室高度方向的变化(假设3)。
可以把它看成是两个柯西课题的叠加如下图。
根据柯西课题,由σh 产生的重分布应力:σσ根据柯西课题,由σh 产生的重分布应力:σhσhσv和σh同时作用时圆形洞室围岩重分布应力:引入天然应力比值系数:σh=λσV则σv和σh同时作用时圆形洞室围岩重分布应力可表示为:(2)圆形洞室重分布应力的特征1)洞壁上的重分布应力为考察洞壁上的重分布应力的特点令:r =R0代入上式,得洞壁上的重分布应力为:①②由上式可知,洞壁上的重分布应力具有下列特点: ① 洞壁上的τr θ=0,σr =0,为单向应力状态; ② σθ大小与洞室尺寸R0无关 ;③ 当θ=0、180°(侧壁),σθ=3σV —σh=(3—λ)σV ; ④ 当θ=90、270°(顶底),σθ=3σh —σV=(3λ—1)σV ; ⑤ 当λ<1/3时,洞顶底将出现拉应力 ; ⑥ 当1/3<λ<3时,σθ为压应力;⑦ 当λ>3时,洞壁两侧出现拉应力,洞顶底出现较高的压应力集中;圆形洞室洞壁切向应力σθ随角θ的变化规律:(图中λ为天然应力比值系数,即侧压力系数 )31=λVσσθ3=λ2=λ1=λ02461-θXY2)静水压力式天然应力场中的围岩重分布应力静水压力式天然应力场是指水平天然应力与铅直天然应力相等的应力场,即λ=1。
把λ=1(即σv=σh=σ0)代入②式,得静水压力式天然应力场中的围岩重分布应力为:由上式可知,静水压力式天然应力场中的围岩重分布应力具有下列特点:①围岩内重分布应力与θ角无关,仅与R0和σ0有关;②由于τrθ=0,则σr,σθ均为主应力,且σθ恒为最大主应力,σr 恒为最小主应力;③当r=R0(洞壁)时,σr=0,σθ=2σ0,可知洞壁上的应力差最大,且处于单向受力状态,说明洞壁最易发生破坏④r增大,σr增大,σθ减小,都渐趋于σ0值(见下图);⑤在理论上,σr,σθ要在r→∞处才达到σ0值,但实际上σr、σθ趋近于σ0的速度很快,当r=6R0时,σr和σθ与σ0就很接近,如图;所以,一般认为,地下洞室开挖引起的围岩重分布应力范围为6R0。
(2)其他形状洞室重分布应力的特征1)应力集中系数的概念为了最有效和经济地利用地下空间,地下建筑的断面常需根据实际需要,开挖成非圆形的各种形状。
但非圆形洞室的围岩应力很难用解析解表示。
由圆形洞室围岩重分布应力分析可知,重分布应力的最大值在洞壁上,且仅有σθ,因此只要洞壁围岩在重分布应力σθ的作用下不发生破坏,那么洞室内部围岩也是稳定的。
为了研究各种洞形洞壁上的重分布应力及其变化情况,引进应力集中系数的概念。
应力集中系数:是指地下洞室开挖后洞壁上一点的应力与开挖前洞壁处该点天然应力的比值。
该系数反映了洞壁各点开挖前后应力的变化情况。
应力集中系数一般用α,β表示,其大小仅与该点的位置有关。
对于圆形洞室,改写为:所以,圆形洞室应力集中系数α=1-2cos2θ,β=1+2cos2θ2)各种形状洞室重分布应力特点:①椭圆形洞室:长轴两端点应力集中最大,易引起压碎破坏;短轴两端易拉应力集中,不利于围岩稳定;(图中N为侧压力系数)②各种形状洞室的角点或急拐弯处应力集中最大,如正方形或矩形洞室角点等。
③长方形短边中点应力集中大于长边中点,而角点处应力集中最大,围岩最易失稳。
④当岩体中天然应力σh和σv相差不大时,以圆形洞室围岩应力分布最均匀,围岩稳定性最好。
⑤当岩体中天然应力σh和σv相差较大时(高地应力区),则应尽量使洞室长轴平行于最大天然应力的作用方向。
⑥ 在天然应力很大的岩体中,洞室断面应尽量采用曲线形,以避免角点上过大的应力集中。
h 大2、塑性围岩重分布应力地下开挖后,洞壁的应力集中最大,当它超过围岩屈服极限时,洞壁围岩就由弹性状态转化为塑性状态,并在围岩中形成一个塑性松动圈。
随着距洞壁距离增大,径向应力σr由零逐渐增大,应力状态由洞壁的单向应力状态逐渐转化为双向应力状态,围岩也就由塑性状态逐渐转化为弹性状态。
弹性区以外则是应力基本未产生变化的天然应力区(或称原岩应力区)。
塑性松动圈的出现,使圈内一定范围内的应力因释放而明显降低,而最大应力集中由原来的洞壁移至塑、弹圈交界处,使弹性区的应力明显升高。
一般采用弹塑性理论求解塑性圈内的围岩重分布应力。
假设:①在均质、连续、各向同性的岩体中开挖一半径为a的洞室,开挖后形成的塑性松动圈半径为R;②岩体天然应力为:σh=σv=σ0(即λ=1);③圈内岩体强度服从莫尔直线强度条件。
由ΣF=0,得沿r 方向的平衡方程式:解方程组,利用边界条件 时, 得塑性区应力: 径向应力为:切向应力为:剪 应力: (因为λ=1属轴对称问题)aR2sin 2)()(=++++-θθθσσσσθd dr rd dr r d d r r r 0=--rdrd r r σσσθφφσσσσθθCctg rr2sin ++-=又由莫尔强度条件:(1)a r =σσar =φφφφφφφφθφφσσσσCctg Cctg Cctg Cctg ar araa r -+-=-+=--)()(sin 1sin 2sin 1sin 2)(sin 1sin 2)(0=τθr(4)塑性圈内围岩重分布应力与岩体天然应力(σ0)无关,而取决于支护力(σa)和岩体强度(C ,φ)值。
(5)若弹性区边界上的径向应力为σR ,则弹性区的应力:由图可见: (1)塑性区内σθ降低了很多,硐壁上降低最多,但并不为零。
(说明岩石产生了塑性变形后还具有一定的承载能力); (2)在弹性区σθ略有升高。
(这是因为在塑性区内,一部分应力释放了,一部分应力则转嫁给弹性区的结果); (3)σr 变化不大,在硐壁上 。
σσa r =rRr R rR r R RVRV r22222222)1()1(σσσσσσθ-+=+-=三、有压洞室围岩重分布应力计算由于洞室内壁上作用有较高的内水压力,使围岩中的重分布应力更加复杂。
应力变化过程如下:• 围岩最初处于开挖后引起的重分布应力之中 • 进行支护衬砌,使围岩重分布应力得到改善• 洞室建成运行后洞内壁作用有内水压力,使围岩中产生一个附加应力 。
内水压力引起的围岩附加应力,可用弹性厚壁筒理论来计算。
由弹性理论可推导厚壁筒内的应力计算公式:若有压洞室半径为R 0,内水压力为pa 则有压洞室围岩重分布应力为:上ra ra r ara aa rpp 22222222)1()1(-+=+-=σσσσθ有压洞室围岩重分布应力σr和σθ由开挖以后围岩重分布应力和内水压力引起的附加应力两项组成。
上式前项为重分布应力,后项为内水压力引起的附加应力值,即:上式表明:内水压力使围岩产生负的切向应力,即拉应力。
当这个切向应力很大时,则常使围岩产生放射状裂隙。
内水压力使围岩产生附加应力的影响范围大致也为6倍洞半径。
第三节围岩压力的类型及影响因素前面我们讲了地下硐室的围岩应力计算及应力分布。
我们将要讨论的围岩压力与围岩应力是两个不同的概念围岩应力:应力重分布影响范围内岩体的应力。
那么什么叫围岩压力呢?他的分布规律如何?又怎样计算围岩压力?首先来看一、围岩压力的概念开挖硐室应力重分布围岩变形、位移重分布应力<围岩强度时,只产生弹性变形或微量塑性变形。
重分布应力≥围岩强度时,围岩破坏(产生裂缝、滑落、滑塌),硐室不稳定状态(影响使用甚至完全丧失使用条件)为了阻止围岩的过大变形和破坏,保证硐室安全稳定,往往必须对硐室进行必要的支护与衬砌———目的是防止岩石塌落和变形,所以支护与衬砌上必然要受到围岩的压力。
——作用在支护与衬砌结构上的围岩变形挤压力或坍塌岩体的重力统称围岩压力。
二、围岩压力类型:围岩压力是由于围岩的过大变形和破坏而产生的,不同岩性、不同结构的岩体,其变形与破坏的机制不同,因而,并非所有的硐室都需要支护与衬砌。
由于硐室的支护与衬砌要消耗大量的木材,水泥及钢材、人力,直接影响工程造价。
因此,在进行设计与施工时,工程人员必须解决这样的问题a. 硐室要不要支护与衬砌?b. 若要,围岩对支护与衬砌的压力又多大?这就是所要解决的问题不同岩性和结构的围岩,其围岩压力类型不同,所采用的评价理论和计算方法也不一样:(1)比较坚硬完整的围岩:一般重分布应力小于弹性极限(不支护或衬砌仍能维持稳定)重分布应力引起的弹性变形在开挖过程中就完成了,因而没有围岩压力或不显现。