2020普陀区初三一模(2020.1.7)

15. 如图 5，在 Rt△ABC 中， C 90 ， AD 是三角形的角平分线，如果 AB 3 5 ， AC 2 5 ，那么点 D 到直线 AB 的距离等于___________. 16. 如图 6，斜坡 AB 长为 100 米，坡角 ABC 30 ，现因“改小坡度”工程的需要，将斜 坡 AB 改造成坡度 i 1: 5 的斜坡 BD （ A 、 D 、 C 三点在地面的同一条垂线上），那么由 点 A 到点 D 下降了_________米（结果保留根号）
将 P 1 t, 2t 代入 y 4 x2 4x 2
3
得 t1
13
129 4
， t2
13 129 4
（舍），
∴
P2
9
129 4
,13
129 2
综上所述：
P1
3 2
, 5
，
P2
9
129 4
,13 129 2
【总结】直角三角形讨论，构造三直角相似
25.【解析】
（1）作高，构建直角三角形，利用三角比来求解， BE 2 ；
13.【答案】 1 3
【解析】三角形的重心及平行线的应用.
14.【答案】 E C
【解析】三角形相似的判定.
15.【答案】2
【解析】勾股定理与角平分线的综合.
16.【答案】 50 10 3
【解析】锐角三角比的应用.
17.【答案】 15 4
【解析】直角三角形的斜边中线与锐角三角比.
18.【答案】 20 13
∴ AP2 AD AC 13 3
∴ AP 3
22.【解析】易得
3 k
k
2
.整理得
k2
2k
3
0

普陀区2020学年度第一学期初三质量调研综 合 试 卷考生注意：1．试卷中第1~20题为物理部分，第21~41题为化学部分，第42题为跨学科案例分析部分。

2．试卷满分135分。

考试时间120分钟。

3．按要求在答题纸上规定的位置作答，在试卷、草稿纸上答题一律无效。

物 理 部 分一、选择题（共12分）下列各题均只有一个正确选项，请将正确选项的代号用2B 铅笔填涂在答题纸的相应位置上，更改答案时，用橡皮擦去，重新填涂。

1． 下列家用电器正常工作电流接近0.2安的是A ．节能灯B ．白炽灯C ．电饭锅D ．空调器2． 如图1所示，人用手触摸静电球时出现了“怒发冲冠”的现象，可以推断竖起的头发丝所带的电荷一定是 A ．正电荷 B ．负电荷 C ．同种电荷 D ．异种电荷3． 如图2所示，盲道上凸起的圆点是为了A ．增大压力B ．减小压力C ．增大压强D ．减小压强4． 在研究电压时，将它比作水压。

这是采用了A ．等效替代法B ．类比法C ．建模法D ．控制变量法5． 甲和乙是由同种材料制成的两导体，长度关系为l 甲＞l 乙，现将它们串联在同一电路中则关于甲和乙的横截面S ，及导体两端电压U 的大小关系，下列判断不成立的是 A ．若S 甲＞S 乙，则U 甲＞U 乙B ．若S 甲＞S 乙，则U 甲＝U 乙C ．若S 甲＜S 乙，则U 甲＞U 乙D ．若S 甲＜S 乙，则U 甲＝U 乙6． 甲、乙两个完全相同的容器中装满两种不同的液体，现将A 、B 两个小球分别浸没在两杯液体中，如图3所示，排开液体的质量相等。

则下列说法中一定正确的是 ① 甲容器对桌面的压力大于乙容器② A 、B 两球受到的浮力相同③ 甲容器中液体对容器底部压力小于乙的④ A 球受到的浮力大于B 球A ．①②③B ．②③C ．①③④D ．③④图1 图2图3二、填空题（共21分）请将结果填入答题纸的相应位置。

7． 我国家庭照明电路电压为________(1)伏，教室中照明灯与控制它的开关是________(2)连接的（选填“串联”或“并联”），照明灯开的越多，电路中的总电阻越________(3)。

上海市普陀区中考数学一模试卷一、选择题：（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上]1.下列函数中，y关于x的二次函数是（） A．y=ax2+bx+c B．y=x（x﹣1）C．D．y=（x﹣1）2﹣x2【分析】根据二次函数的定义，逐一分析四个选项即可得出结论．【解答】解：A、当 a=0 时，y=bx+c 不是二次函数；B、y=x（x﹣1）=x2﹣x 是二次函数；C、y=不是二次函数；D、y=（x﹣1）2﹣x2=﹣2x+1 为一次函数．故选：B．【点评】本题考查了二次函数的定义，牢记二次函数的定义是解题的关键．2.在Rt△ABC中，∠C=90°，AC=2，下列结论中，正确的是（）A．AB=2sinA B．AB=2cosA C．BC=2tanA D．BC=2cotA【分析】直接利用锐角三角函数关系分别计算得出答案．【解答】解：∵∠C=90°，AC=2，∴cosA==，故AB=，故选项 A，B 错误；A ． tanA= = ，则 BC=2tanA ，故选项 C 正确；则选项 D错误．故选：C ．【点评】此题主要考查了锐角三角函数关系，正确将记忆锐角三角函数关系是解题关键． 3. 如图，在△ABC中，点D 、E 分别在边AB 、AC 的反向延长线上，下面比例式中，不能判断ED∥BC的是（）B ．C ．D ．【分析】根据平行线分线段成比例定理，对各选项进行逐一判断即可．【解答】解：A ．当时，能判断ED∥BC； B. 当时，能判断ED∥BC； C. 当时，不能判断ED∥BC； D. 当时，能判断ED∥BC；故选：C ．【点评】本题考查的是平行线分线段成比例定理，如果一条直线截三角形的两边 （或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边．4.已知，下列说法中，不正确的是（）A．B．与方向相同C．D．【分析】根据平行向量以及模的定义的知识求解即可求得答案，注意掌握排除法在选择题中的应用．【解答】解：A、错误．应该是﹣5=；B、正确．因为，所以与的方向相同；C、正确．因为，所以∥；D、正确．因为，所以||=5||；故选：A．【点评】本题考查了平面向量，注意，平面向量既有大小，又由方向，平行向量，也叫共线向量，是指方向相同或相反的非零向量．零向量和任何向量平行．5.如图，在平行四边形ABCD中，F是边AD上的一点，射线CF和BA的延长线交于点E，如果，那么的值是（）A．B．C．D．【分析】根据相似三角形的性质进行解答即可．【解答】解：∵在平行四边形 ABCD 中，∴AE∥CD，∴△EAF∽△CDF，∵，∴，∴，∵AF∥BC，∴△EAF∽△EBC，∴=，故选：D．【点评】此题考查相似三角形的判定和性质，综合运用了平行四边形的性质和相似三角形的性质是解题关键．6.如图，已知AB和CD是⊙O的两条等弦．OM ⊥AB，ON⊥CD，垂足分别为点M、N，BA、DC的延长线交于点P，联结OP．下列四个说法中：①；②OM=ON；③PA=PC；④∠BPO=∠DPO，正确的个数是（）A．1 B．2 C．3 D．4【分析】如图连接 OB、OD，只要证明Rt△OMB≌Rt△OND，Rt△OPM≌Rt△OPN 即可解决问题．【解答】解：如图连接 OB、OD；∵AB=CD，∴=，故①正确∵OM⊥AB，ON⊥CD，∴AM=MB，CN=ND，∴BM=DN，∵OB=OD，∴Rt△OMB≌Rt△OND，∴OM=ON，故②正确，∵OP=OP，∴Rt△OPM≌Rt△OPN，∴PM=PN，∠OPB=∠OPD，故④正确，∵AM=CN，∴PA=PC，故③正确，故选：D．【点评】本题考查垂径定理、圆心角、弧、弦的关系、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线面构造全等三角形解决问题，属于中考常考题型．二．填空题（本大题共 12 题，每题 4 分，满分 48 分）7．如果 =，那么= ．【分析】利用比例的性质由=得到=，则可设a=2t，b=3t，然后把a=2t，b=3t代入中进行分式的运算即可．【解答】解：∵=，∴=，设 a=2t，b=3t，∴==．故答案为．【点评】本题考查了比例的性质：常用的性质有：内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质．8．已知线段a=4厘米，b=9厘米，线段c是线段a和线段b的比例中项，线段c的长度等于6厘米．【分析】根据比例中项的定义，列出比例式即可得出中项，注意线段不能为负．【解答】解：根据比例中项的概念结合比例的基本性质，得：比例中项的平方等于两条线段的乘积．所以c2=4×9，解得c=±6（线段是正数，负值舍去），∴c=6cm，故答案为：6．【点评】本题考查比例线段、比例中项等知识，解题的关键是熟练掌握基本概念，属于中考常考题型．9．化简：=﹣4+7 ．【分析】根据屏幕绚丽的加法法则计算即可【解答】解：：=﹣4+6=﹣4+7，故答案为；【点评】本题考查平面向量的加减法则，解题的关键是熟练掌握平面向量的加减法则，注意平面向量的加减适合加法交换律以及结合律，适合去括号法则．10.在直角坐标系平面内，抛物线y=3x2+2x在对称轴的左侧部分是下降的（填“上升”或“下降”）【分析】由抛物线解析式可求得其开口方向，再结合二次函数的增减性则可求得答案．【解答】解：∵在 y=3x2+2x 中，a=3＞0，∴抛物线开口向上，∴在对称轴左侧部分 y 随 x 的增大而减小，即图象是下降的，故答案为：下降．【点评】本题主要考查二次函数的性质，利用二次函数的解析式求得抛物线的开口方向是解题的关键．11.二次函数y=（x﹣1）2﹣3的图象与y轴的交点坐标是（0，﹣2）．【分析】求自变量为0时的函数值即可得到二次函数的图象与y轴的交点坐标．【解答】解：把x=0代入y=（x﹣1）2﹣3得y=1﹣3=﹣2，所以该二次函数的图象与y轴的交点坐标为（0，﹣2），故答案为（0，﹣2）．【点评】本题考查了二次函数图象上点的坐标特征，在y轴上的点的横坐标为0．12.将抛物线y=2x2平移，使顶点移动到点P（﹣3，1）的位置，那么平移后所得新抛物线的表达式是y=2（x+3）2+1 ．【分析】由于抛物线平移前后二次项系数不变，然后根据顶点式写出新抛物线解析式．【解答】解：抛物线 y=2x2 平移，使顶点移到点 P（﹣3，1）的位置，所得新抛物线的表达式为 y=2（x+3）2+1．故答案为：y=2（x+3）2+1．【点评】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．13.在直角坐标平面内有一点A（3，4），点A与原点O的连线与x轴的正半轴夹角为α，那么角α的余弦值是．【分析】利用锐角三角函数的定义、坐标与图形性质以及勾股定理的知识求解．【解答】解：∵在直角坐标平面内有一点A（3，4），∴OA==5，∴cosα= ．故答案为：．【点评】本题考查了解直角三角形、锐角三角函数的定义、坐标与图形性质以及勾股定理的知识，此题比较简单，易于掌握．14.如图，在△ABC中，AB=AC，点D、E分别在边BC、AB上，且∠ADE=∠B，如果DE：AD=2：5，BD=3，那么AC= ，．【分析】根据∠ADE=∠B，∠EAD=∠DAB，得出△AED∽△ABD，利用相似三角形的性质解答即可．【解答】解：∵∠ADE=∠B，∵∠EAD=∠DAB，∴△AED∽△ABD，∴，即，∴AB=，∵AB=AC，∴AC=，故答案为：，【点评】本题考查了相似三角形的判定与性质．关键是要懂得找相似三角形，利用相似三角形的性质求解．15.如图，某水库大坝的横断面是梯形ABCD，坝顶宽AD=6米，坝高是20 米，背水坡 AB的坡角为30°，迎水坡CD的坡度为1：2，那么坝底 BC 的长度等于（46+20）米（结果保留根号）【分析】过梯形上底的两个顶点向下底引垂线AE、DF，得到两个直角三角形和一个矩形，分别解Rt△ABE、Rt△DCF求得线段BE、CF的长，然后与EF 相加即可求得 BC 的长．【解答】解：如图，作AE⊥BC，DF⊥BC，垂足分别为点E，F，则四边形ADFE 是矩形．由题意得，EF=AD=6 米，AE=DF=20 米，∠B=30°，斜坡 CD 的坡度为 1： 2，在Rt△ABE 中，∵∠B=30°，∴BE=AE=20米．在Rt△CFD中，∵=，∴CF=2DF=40 米，∴BC=BE+EF+FC=20+6+40=46+20（米）．所以坝底BC的长度等于（46+20）米．故答案为（46+20）．【点评】此题考查了解直角三角形的应用﹣坡度坡角问题，难度适中，解答本题的关键是构造直角三角形和矩形，注意理解坡度与坡角的定义．16.已知Rt△ABC中，∠C=90°，AC=3，BC=，CD⊥AB，垂足为点D，以点D为圆心作⊙D，使得点A在⊙D外，且点B在⊙D内．设⊙D的半径为r，那么r的取值范围是．【分析】先根据勾股定理求出AB的长，进而得出CD的长，由点与圆的位置关系即可得出结论．【解答】解：∵Rt△ABC中，∠ACB=90，AC=3，BC=，∴AB==4．∵CD⊥AB，∴CD=．∵AD•BD=CD2，设AD=x，BD=4﹣x．解得x=∴点 A 在圆外，点 B 在圆内，r的范围是，故答案为：．【点评】本题考查的是点与圆的位置关系，熟知点与圆的三种位置关系是解答此题的关键．17.如图，点D在△ABC的边BC上，已知点E、点F分别为△ABD和△ADC 的重心，如果BC=12，那么两个三角形重心之间的距离EF的长等于4 ．【分析】连接AE并延长交BD于 G，连接AF并延长交CD于 H，根据三角形的重心的概念、相似三角形的性质解答．【解答】解：如图，连接 AE 并延长交 BD 于 G，连接 AF 并延长交 CD 于 H，∵点 E、F 分别是△ABD 和△ACD 的重心，∴DG=BD，DH=CD，AE=2GE，AF=2HF，∵BC=12，∴GH=DG+DH= （BD+CD）= BC= ×12=6，∵AE=2GE，AF=2HF，∠EAF=∠GAH，∴△EAF∽△GAH，∴==，∴EF=4，故答案为：4．【点评】本题考查了三角形重心的概念和性质，三角形的重心是三角形中线的交点，三角形的重心到顶点的距离等于到对边中点的距离的2倍．18.如图，△ABC中，AB=5，AC=6，将△ABC翻折，使得点A落到边BC 上的点A′处，折痕分别交边AB、AC于点E，点F，如果A′F∥AB，那么BE= ．【分析】设BE=x，则AE=5﹣x=AF=A'F，CF=6﹣（5﹣x）=1+x，依据△A'CF ∽△BCA，可得=，即=，进而得到BE=．【解答】解：如图，由折叠可得，∠AFE=∠A'FE，∵A'F∥AB，∴∠AEF=∠A'FE，∴∠AEF=∠AFE，∴AE=AF，由折叠可得，AF=A'F，设 BE=x，则 AE=5﹣x=AF=A'F，CF=6﹣（5﹣x）=1+x，∵A'F∥AB，∴△A'CF∽△BCA，∴=，即=，解得x=，∴BE=，故答案为：．【点评】本题主要考查了折叠问题以及相似三角形的判定与性质的运用，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，对应边和对应角相等．三、解答题（本大题共 7 题，满分 78 分）19．（10分）计算：45°．【分析】直接利用特殊角的三角函数值进而代入化简得出答案．【解答】解：原式=﹣×= ﹣= ．【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键． 20．（10分）已知一个二次函数的图象经过A（0，﹣3），B（1，0），C（m，2m+3），D（﹣1，﹣2）四点，求这个函数解析式以及点C的坐标．【分析】设一般式y=ax2+bx+c，把A、B、D点的坐标代入得，然后解法组即可得到抛物线的解析式，再把 C（m，2m+3）代入解析式得到关于 m 的方程，解关于 m 的方程可确定 C 点坐标．【解答】解：设抛物线的解析式为 y=ax2+bx+c，把A（0，﹣3），B（1，0），D（﹣1，﹣2）代入得，解得，∴抛物线的解析式为 y=2x2+x﹣3，把C（m，2m+3）代入得2m2+m﹣3=2m+3，解得m1=﹣，m2=2，∴C点坐标为（﹣，0）或（2，7）．【点评】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与 x 轴有两个交点时，可选择设其解析式为交点式来求解．21．（10分）如图，已知⊙O经过△ABC的顶点A、B，交边BC于点D，点A恰为的中点，且BD=8，AC=9，sinC=，求⊙O的半径．【分析】如图，连接OA．交BC于H．首先证明OA⊥BC，在Rt△ACH中，求出AH，设⊙O的半径为r，在Rt△BOH中，根据BH2+OH2=OB2，构建方程即可解决问题；【解答】解：如图，连接 OA．交 BC 于 H．∵点A为的中点，∴OA⊥BD，BH=DH=4，∴∠AHC=∠BHO=90°，∵sinC==，AC=9，∴AH=3，设⊙O 的半径为 r，在Rt△BOH 中，∵BH2+OH2=OB2，∴42+（r﹣3）2=r2，∴r=，∴⊙O的半径为．【点评】本题考查圆心角、弧、弦的关系、垂径定理、勾股定理、锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．22．（10分）下面是一位同学的一道作图题：已知线段a、b、c（如图），求作线段x，使a：b=c：x他的作法如下：（1）、以点O为端点画射线OM，ON．（2）、在OM上依次截取OA=a，AB=b．（3）、在ON上截取OC=c．（4）、联结AC，过点B作BD∥AC，交ON于点D．所以：线段CD就是所求的线段x．①试将结论补完整②这位同学作图的依据是平行于三角形一边的直线截其它两边（或两边的延长线），所得对应线段成比例③如果OA=4，AB=5，，试用向量表示向量．【分析】①根据作图依据平行线分线段成比例定理求解可得；②根据“平行于三角形一边的直线截其它两边（或两边的延长线），所得对应线段成比例”可得；③先证△OAC∽△OBD得= ，即BD= AC，从而知= =﹣=﹣．【解答】解：①根据作图知，线段 CD 就是所求的线段 x，故答案为：CD；②这位同学作图的依据是：平行于三角形一边的直线截其它两边（或两边的延长线），所得对应线段成比例；故答案为：平行于三角形一边的直线截其它两边（或两边的延长线），所得对应线段成比例；③∵OA=4、AB=5，且BD∥AC，∴△OAC∽△OBD，∴=，即=，∴BD=AC，∴= =﹣=﹣．【点评】本题主要考查作图﹣复杂作图，解题的关键是熟练掌握平行线分线段成比例定理及向量的计算．23．（12分）已知：如图，四边形ABCD的对角线AC和BD相交于点E，AD=DC，DC2=DE•DB，求证：（1）△BCE∽△ADE；（2）AB•BC=BD•BE．【分析】（1）由∠DAC=∠DCA，对顶角∠AED=∠BEC，可证△BCE∽△ADE．（2）根据相似三角形判定得出△ADE∽△BDA，进而得出△BCE∽△BDA，利用相似三角形的性质解答即可．【解答】证明：（1）∵AD=DC，∴∠DAC=∠DCA，∵DC2=DE•DB，∴=，∵∠CDE=∠BDC，∴△CDE∽△BDC，∴∠DCE=∠DBC，∴∠DAE=∠EBC，∵∠AED=∠BEC，∴△BCE∽△ADE，（2）∵DC2=DE•DB，AD=DC∴AD2=DE•DB，同法可得△ADE∽△BDA，∴∠DAE=∠ABD=∠EBC，∵△BCE∽△ADE，∴∠ADE=∠BCE，∴△BCE∽△BDA，∴= ，∴AB•BC=BD•BE．【点评】本题考查了相似三角形的判定与性质．关键是要懂得找相似三角形，利用相似三角形的性质求解．24．（12分）如图，已知在平面直角坐标系中，已知抛物线y=ax2+2ax+c（其中a、c为常数，且a＜0）与x轴交于点A，它的坐标是（﹣3，0），与y轴交于点B，此抛物线顶点C到x轴的距离为4（1）求抛物线的表达式；（2）求∠CAB的正切值；（3）如果点P是抛物线上的一点，且∠ABP=∠CAO，试直接写出点P的坐标．【分析】（1）先求得抛物线的对称轴方程，然后再求得点 C 的坐标，设抛物线的解析式为y=a（x+1）2+4，将点（﹣3，0）代入求得a的值即可；（2）先求得A、B、C的坐标，然后依据两点间的距离公式可得到BC、AB、AC的长，然后依据勾股定理的逆定理可证明∠ABC=90°，最后，依据锐角三角函数的定义求解即可；（3）记抛物线与x轴的另一个交点为D．先求得D（1，0），然后再证明∠DBO=∠CAB，从而可证明∠CAO=ABD，故此当点P与点D重合时，∠ABP=∠CAO；当点P在AB的上时．过点P作PE∥AO，过点B作BF∥AO，则PE∥BF．先证明∠EPB=∠CAB，则tan∠EPB=，设BE=t，则PE=3t，P（﹣3t，3+t），将P（﹣3t，3+t）代入抛物线的解析式可求得t的值，从而可得到点P 的坐标．【解答】解：（1）抛物线的对称轴为x=﹣=﹣1．∵a＜0，∴抛物线开口向下．又∵抛物线与 x 轴有交点，∴C 在 x 轴的上方，∴抛物线的顶点坐标为（﹣1，4）．设抛物线的解析式为 y=a（x+1）2+4，将点（﹣3，0）代入得：4a+4=0，解得：a=﹣1，∴抛物线的解析式为 y=﹣x2﹣2x+3．（2）将x=0代入抛物线的解析式得：y=3，∴B（0，3）．∵C（﹣1，4）、B（0，3）、A（﹣3，0），∴BC=，AB=3，AC=2，∴BC2+AB2=AC2，∴∠ABC=90°．∴tan∠CAB==．（3）如图1所示：记抛物线与x轴的另一个交点为D．∵点 D 与点 A 关于 x=﹣1 对称，∴D（1，0）．∴tan∠DBO=．又∵由（2）可知：tan∠CAB=．∴∠DBO=∠CAB．又∵OB=OA=3，∴∠BAO=∠ABO．∴∠CAO=∠ABD．∴当点 P 与点 D 重合时，∠ABP=∠CAO，∴P（1，0）．如图2所示：当点P在AB的上时．过点P作PE∥AO，过点B作BF∥AO，则PE∥BF．∵BF∥AO，∴∠BAO=∠FBA．又∵∠CAO=∠ABP，∴∠PBF=∠ CAB．又∵PE∥BF，∴∠EPB=∠PBF，∴∠EPB=∠CAB．∴tan∠EPB=．设BE=t，则PE=3t，P（﹣3t，3+t）．将P（﹣3t，3+t）代入抛物线的解析式得：y=﹣x2﹣2x+3得：﹣9t2+6t+3=3+t，解得t=0（舍去）或t=．∴P（﹣，）．综上所述，点P的坐标为P（1，0）或P（﹣，）．【点评】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、勾股定理的逆定理、等腰直角三角形的性质、锐角三角函数的定义，用含 t 的式子表示点 P 的坐标是解题的关键．25．（14分）如图1，∠BAC的余切值为2，AB=2，点D是线段AB上的一动点（点D不与点A、B重合），以点D为顶点的正方形DEFG的另两个顶点E、F都在射线AC上，且点F在点E的右侧，联结BG，并延长BG，交射线EC于点P．（1）点D在运动时，下列的线段和角中，④⑤是始终保持不变的量（填序号）；①AF；②FP；③BP；④∠BDG；⑤∠GAC；⑥∠BPA；（2）设正方形的边长为x，线段AP的长为y，求y与x之间的函数关系式，并写出定义域；（3）如果△PFG与△AFG相似，但面积不相等，求此时正方形的边长．【分析】（1）作BM⊥AC于M，交DG于N，如图，利用三角函数的定义得到=2，设BM=t，则AM=2t，利用勾股定理得（2t）2+t2=（2）2，解得t=2，即BM=2，AM=4，设正方形的边长为x，则AE=2x，AF=3x，由于tan∠GAF==，则可判断∠GAF为定值；再利用DG∥AP得到∠BDG=∠BAC，则可判断∠BDG为定值；在Rt△BMP中，利用勾股定理和三角函数可判断PB在变化，∠BPM在变化，PF在变化；（2）易得四边形DEMN为矩形，则NM=DE=x，证明△BDG∽△BAP，利用相似比可得到y与x的关系式；（3）由于∠AFG=∠PFG=90°，△PFG与△AFG相似，且面积不相等，利用相似比得到PF=x，讨论：当点P在点F点右侧时，则AP=x，所以=x，当点P在点F点左侧时，则AP= x，所以=x，然后分别解方程即可得到正方形的边长．【解答】解：（1）作BM⊥AC于M，交DG于N，如图，在Rt△ABM中，∵cot∠BAC==2，设 BM=t，则 AM=2t，∵AM2+BM2=AB2，∴（2t）2+t2=（2）2，解得t=2，∴BM=2，AM=4，设正方形的边长为 x，在Rt△ADE中，∵cot∠DAE==2，∴AE=2x，∴AF=3x，在Rt△GAF中，tan∠GAF===，∴∠GAF 为定值；∵DG∥AP，∴∠BDG=∠BAC，∴∠BDG 为定值；在Rt△BMP中，PB=，而PM在变化，∴PB 在变化，∠BPM 在变化，∴PF 在变化，所以∠BDG 和∠GAC 是始终保持不变的量；故答案为④⑤；（2）易得四边形DEMN为矩形，则NM=DE=x，∵DG∥AP，∴△BDG∽△BAP，∴=，即=，∴y=（1≤x＜2）（3）∵∠AFG=∠PFG=90°，△PFG与△AFG相似，且面积不相等，∴=，即=，∴PF=x，当点P在点F点右侧时，AP=x，∴=x，解得x=，当点P在点F点左侧时，AP=AF﹣PF=3x﹣x=x，∴=x，解得x=，综上所述，正方形的边长为或．【点评】本题考查了相似形综合题：熟练掌握锐角三角函数的定义、正方形的性质和相似三角形的判定与性质．。

78 分）
19．解：原式
2 ( 3)2 1
2
2 ···································································（ 4 分）
( 3) 2 4 2
2
31
2 2 ······················································································（ 3 分） 3 22
．
y y5
2．下列二次函数中，如果函数图像的对称轴是
y 轴，那么这个函数是（ ▲ ）
（ A ） y x2 2x ； （B ） y x2 2 x 1； （C） y x2 2 ； （D ） y ( x 1)2 ．
1 3．已知在 Rt△ ABC 中， C 90 ， sin A ，那么下列说法中正确的是（
3
A
A
A
D
D
B
图6
C
C
17．如图 7，在四边形 ABCD 中， ABC
O B 图8
B 图7
90 ，对角线 AC 、 BD 交于点 O ， AO
C
CO ，
CD BD ，如果 CD 3 ， BC 5 ，那么 AB
▲．
18．如图 8，在 Rt△ ABC 中， C 90 ， AC 5 ，sin B 5 ，点 P 为边 BC 上一点， PC 3 ， 13
∵ DE 5 ，∴ BF 5 ． ·····································································（ 1 分）
∵ DE // BC ，

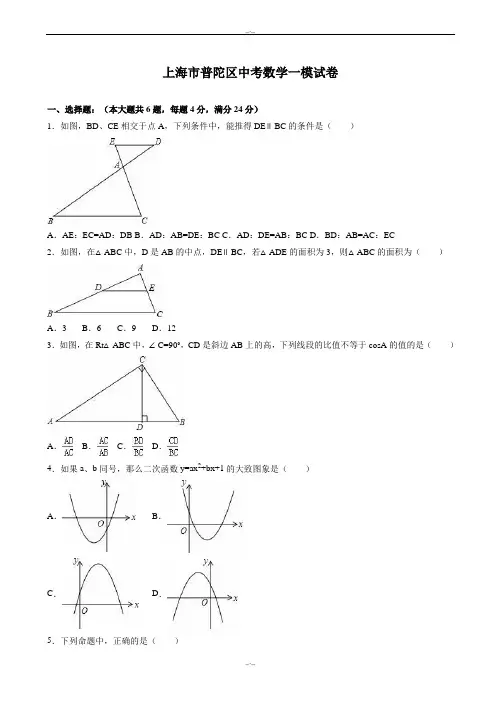
上海市普陀区中考数学一模试卷一、选择题：（本大题共6题，每题4分，满分24分）1．如图，BD、CE相交于点A，下列条件中，能推得DE∥BC的条件是（）A．AE：EC=AD：DB B．AD：AB=DE：BC C．AD：DE=AB：BC D．BD：AB=AC：EC2．如图，在△ABC中，D是AB的中点，DE∥BC，若△ADE的面积为3，则△ABC的面积为（）A．3 B．6 C．9 D．123．如图，在Rt△ABC中，∠C=90°，CD是斜边AB上的高，下列线段的比值不等于cosA的值的是（）A．B．C．D．4．如果a、b同号，那么二次函数y=ax2+bx+1的大致图象是（）A．B．C．D．5．下列命题中，正确的是（）A．圆心角相等，所对的弦的弦心距相等B．三点确定一个圆C．平分弦的直径垂直于弦，并且平分弦所对的弧D．弦的垂直平分线必经过圆心6．已知在平行四边形ABCD中，点M、N分别是边BC、CD的中点，如果=，=，那么向量关于、的分解式是（）A．﹣B．﹣+C．+D．﹣﹣二、填空题：（本大题共12题，每题4分，满分48分）7．如果，那么=．8．计算：2（+）+（﹣）=．9．计算：sin245°+cot30°•tan60°=．10．已知点P把线段分割成AP和PB两段（AP＞PB），如果AP是AB和PB的比例中项，那么AP：AB 的值等于．11．在函数①y=ax2+bx+c，②y=（x﹣1）2﹣x2，③y=5x2﹣，④y=﹣x2+2中，y关于x的二次函数是．（填写序号）12．二次函数y=x2+2x﹣3的图象有最点．（填：“高”或“低”）13．如果抛物线y=2x2+mx+n的顶点坐标为（1，3），那么m+n的值等于．14．如图，点G为△ABC的重心，DE经过点G，DE∥AC，EF∥AB，如果DE的长是4，那么CF的长是．15．半圆形纸片的半径为1cm，用如图所示的方法将纸片对折，使对折后半圆弧的中点M与圆心O重合，则折痕CD的长为cm．16．已知在Rt△ABC中，∠C=90°，点P、Q分别在边AB、AC上，AC=4，BC=AQ=3，如果△APQ与△ABC 相似，那么AP的长等于．17．某货站用传送带传送货物，为了提高传送过程的安全性，工人师傅将原坡角为45°的传送带AB，调整为坡度i=1：的新传送带AC（如图所示）．已知原传送带AB的长是4米．那么新传送带AC的长是米．18．已知A（3，2）是平面直角坐标中的一点，点B是x轴负半轴上一动点，联结AB，并以AB为边在x 轴上方作矩形ABCD，且满足BC：AB=1：2，设点C的横坐标是a，如果用含a的代数式表示D点的坐标，那么D点的坐标是．三、解答题：（本大题共7题，满分78分）19．已知：如图，在梯形ABCD中，AD∥BC，AD=，点M是边BC的中点=，=（1）填空：=，=（结果用、表示）（2）直接在图中画出向量2+．（不要求写作法，但要指出图中表示结论的向量）20．将抛物线y=先向上平移2个单位，再向左平移m（m＞0）个单位，所得新抛物线经过点（﹣1，4），求新抛物线的表达式及新抛物线与y轴交点的坐标．21．如图，已知AD是⊙O的直径，AB、BC是⊙O的弦，AD⊥BC，垂足是点E，BC=8，DE=2，求⊙O 的半径长和sin∠BAD的值．22．已知：如图，有一块面积等于1200cm2的三角形纸片ABC，已知底边与底边BC上的高的和为100cm （底边BC大于底边上的高），要把它加工成一个正方形纸片，使正方形的一边EF在边BC上，顶点D、G分别在边AB、AC上，求加工成的正方形铁片DEFG的边长．23．已知，如图，在四边形ABCD中，∠ADB=∠ACB，延长AD、BC相交于点E．求证：（1）△ACE∽△BDE；（2）BE•DC=AB•DE．24．已知，如图，在平面直角坐标系xOy中，二次函数y=ax2﹣的图象经过点、A（0，8）、B（6，2）、C（9，m），延长AC交x轴于点D．（1）求这个二次函数的解析式及的m值；（2）求∠ADO的余切值；（3）过点B的直线分别与y轴的正半轴、x轴、线段AD交于点P（点A的上方）、M、Q，使以点P、A、Q为顶点的三角形与△MDQ相似，求此时点P的坐标．25．如图，已知锐角∠MBN的正切值等于3，△PBD中，∠BDP=90°，点D在∠MBN的边BN上，点P在∠MBN内，PD=3，BD=9，直线l经过点P，并绕点P旋转，交射线BM于点A，交射线DN于点C，设=x（1）求x=2时，点A到BN的距离；（2）设△ABC的面积为y，求y关于x的函数解析式，并写出函数的定义域；（3）当△ABC因l的旋转成为等腰三角形时，求x的值．上海市普陀区中考数学一模试卷参考答案与试题解析一、选择题：（本大题共6题，每题4分，满分24分）1．如图，BD、CE相交于点A，下列条件中，能推得DE∥BC的条件是（）A．AE：EC=AD：DB B．AD：AB=DE：BC C．AD：DE=AB：BC D．BD：AB=AC：EC【考点】平行线分线段成比例．【分析】根据比例式看看能不能推出△ABC∽△ADE即可．【解答】解：A、∵AE：EC=AD：DB，∴=，∴都减去1得：=，∵∠BAC=∠EAD，∴△ABC∽△ADE，∴∠D=∠B，∴DE∥BC，故本选项正确；B、根据AD：AB=DE：BC不能推出△ABC∽△ADE，即不能得出内错角相等，不能推出DE∥BC，故本选项错误；C、根据AD：DE=AB：BC不能推出△ABC∽△ADE，即不能得出内错角相等，不能推出DE∥BC，故本选项错误；D、根据BD：AB=AC：EC不能推出△ABC∽△ADE，即不能得出内错角相等，不能推出DE∥BC，故本选项错误；故选A．【点评】本题考查了平行线分线段成比例定理的应用，能理解平行线分线段成比例定理的内容是解此题的关键．2．如图，在△ABC中，D是AB的中点，DE∥BC，若△ADE的面积为3，则△ABC的面积为（）A．3 B．6 C．9 D．12【考点】相似三角形的判定与性质；三角形中位线定理．【分析】由平行可知△ADE∽△ABC，且=，再利用三角形的面积比等于相似比的平方可求得△ABC的面积．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∵D是AB的中点，∴=，∴=（）2=，且S△ADE=3，∴=，∴S△ABC=12，故选D．【点评】本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．3．如图，在Rt△ABC中，∠C=90°，CD是斜边AB上的高，下列线段的比值不等于cosA的值的是（）A．B．C．D．【考点】锐角三角函数的定义．【分析】根据余角的性质，可得∠=∠BCD，根据余弦等于邻边比斜边，可得答案．【解答】解：A、在Rt△ABD中，cosA=，故A正确；B、在Rt△ABC中，cosA=，故B正确C、在Rt△BCD中，cosA=cos∠BCD=，故C错误；D、在Rt△BCD中，cosA=cos∠BCD=，故D正确；故选：C．【点评】本题考查了锐角三角函数的定义，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．4．如果a、b同号，那么二次函数y=ax2+bx+1的大致图象是（）A．B．C．D．【考点】二次函数的图象．【分析】分a＞0和a＜0两种情况根据二次函数图象的开口方向、对称轴、与y轴的交点情况分析判断即可得解．【解答】解：a＞0，b＞0时，抛物线开口向上，对称轴x=﹣＜0，在y轴左边，与y轴正半轴相交，a＜0，b＜0时，抛物线开口向下，对称轴x=﹣＜0，在y轴左边，与y轴正半轴坐标轴相交，D选项符合．故选D．【点评】本题考查了二次函数图象，熟练掌握函数图象与系数的关系是解题的关键，注意分情况讨论．5．下列命题中，正确的是（）A．圆心角相等，所对的弦的弦心距相等B．三点确定一个圆C．平分弦的直径垂直于弦，并且平分弦所对的弧D．弦的垂直平分线必经过圆心【考点】命题与定理．【分析】根据有关性质和定理分别对每一项进行判断即可．【解答】解：A、在同圆或等圆中，相等的圆心角所对的弦相等，故本选项错误；B、不在一条直线上的三点确定一个圆，错误；C、平分弦的直径不一定垂直于弦，错误；D、弦的垂直平分线必经过圆心，正确；故选D【点评】此题考查了命题与定理，关键是熟练掌握有关性质和定理，能对命题的真假进行判断．6．已知在平行四边形ABCD中，点M、N分别是边BC、CD的中点，如果=，=，那么向量关于、的分解式是（）A．﹣B．﹣+C．+D．﹣﹣【考点】*平面向量．【分析】首先根据题意画出图形，然后连接BD，由三角形法则，求得，又由点M、N分别是边BC、CD 的中点，根据三角形中位线的性质，即可求得答案．【解答】解：如图，连接BD，∵在平行四边形ABCD中，=，=，∴=﹣=﹣，∵点M、N分别是边BC、CD的中点，∴MN∥BD，MN=BD，∴==（﹣）=﹣+．故选B．【点评】此题考查了平面向量的知识以及三角形的中位线的性质．注意结合题意画出图形，利用图形求解是关键．二、填空题：（本大题共12题，每题4分，满分48分）7．如果，那么=．【考点】比例的性质．【分析】根据比例设x=2k，y=5k，然后代入比例式进行计算即可得解．【解答】解：∵=，∴设x=2k，y=5k，则===．故答案为：．【点评】本题考查了比例的性质，利用“设k法”表示出x、y可以使计算更加简便．8．计算：2（+）+（﹣）=3+．【考点】*平面向量．【分析】直接利用平面向量的加减运算法则求解即可求得答案．【解答】解：2（+）+（﹣）=2+2+﹣=3+．故答案为：3+．【点评】此题考查了平面向量的知识．注意掌握去括号法则．9．计算：sin245°+cot30°•tan60°=．【考点】特殊角的三角函数值．【分析】直接利用特殊角的三角函数值代入求出答案．【解答】解：原式=sin245°+cot30°•tan60°=（）2+×=．故答案为：．【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．10．已知点P把线段分割成AP和PB两段（AP＞PB），如果AP是AB和PB的比例中项，那么AP：AB 的值等于．【考点】黄金分割．【分析】根据黄金分割的概念和黄金比是解答即可．【解答】解：∵点P把线段分割成AP和PB两段（AP＞PB），AP是AB和PB的比例中项，∴点P是线段AB的黄金分割点，∴AP：AB=，故答案为：．【点评】本题考查的是黄金分割的概念，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值叫做黄金比．11．在函数①y=ax2+bx+c，②y=（x﹣1）2﹣x2，③y=5x2﹣，④y=﹣x2+2中，y关于x的二次函数是④．（填写序号）【考点】二次函数的定义．【分析】根据形如y=ax2+bx+c（a≠0）是二次函数，可得答案．【解答】解：①a=0时y=ax2+bx+c是一次函数，②y=（x﹣1）2﹣x2是一次函数；③y=5x2﹣不是整式，不是二次函数；④y=﹣x2+2是二次函数，故答案为：④．【点评】本题考查了二次函数，形如y=ax2+bx+c（a≠0）是二次函数，注意二次项的系数不能为零．12．二次函数y=x2+2x﹣3的图象有最低点．（填：“高”或“低”）【考点】二次函数的最值．【分析】直接利用二次函数的性质结合其开口方向得出答案．【解答】解：∵y=x2+2x﹣3，a=1＞0，∴二次函数y=x2+2x﹣3的图象有最低点．故答案为：低．【点评】此题主要考查了二次函数的性质，得出二次函数的开口方向是解题关键．13．如果抛物线y=2x2+mx+n的顶点坐标为（1，3），那么m+n的值等于1．【考点】二次函数的性质．【专题】推理填空题．【分析】根据抛物线y=2x2+mx+n的顶点坐标为（1，3），可知，从而可以得到m、n的值，进而可以得到m+n的值．【解答】解：∵抛物线y=2x2+mx+n的顶点坐标为（1，3），∴，解得m=﹣4，n=5，∴m+n=﹣4+5=1．故答案为：1．【点评】本题考查二次函数的性质，解题的关键是明确二次函数的顶点坐标公式．14．如图，点G为△ABC的重心，DE经过点G，DE∥AC，EF∥AB，如果DE的长是4，那么CF的长是2．【考点】三角形的重心．【分析】连接BD并延长交AC于H，根据重心的性质得到=，根据相似三角形的性质求出AC，根据平行四边形的判定和性质求出AF，计算即可．【解答】解：连接BD并延长交AC于H，∵点G为△ABC的重心，∴=，∵DE∥AC，∴△BDE∽△BAC，∴==，又DE=4，∴AC=6，∵DE∥AC，EF∥AB，∴四边形ADEF是平行四边形，∴AF=DE=4，∴CF=AC﹣AF=2，故答案为：2．【点评】此题考查了重心的概念和性质：三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．15．半圆形纸片的半径为1cm，用如图所示的方法将纸片对折，使对折后半圆弧的中点M与圆心O重合，则折痕CD的长为cm．【考点】垂径定理；勾股定理．【分析】作MO交CD于E，则MO⊥CD．连接CO．根据勾股定理和垂径定理求解．【解答】解：作MO交CD于E，则MO⊥CD，连接CO，对折后半圆弧的中点M与圆心O重合，则ME=OE=OC，在直角三角形COE中，CE==，折痕CD的长为2×=（cm）．【点评】作出辅助线，构造直角三角形，根据对称性，利用勾股定理解答．16．已知在Rt△ABC中，∠C=90°，点P、Q分别在边AB、AC上，AC=4，BC=AQ=3，如果△APQ与△ABC 相似，那么AP的长等于或．【考点】相似三角形的性质．【分析】根据勾股定理求出AB的长，根据相似三角形的性质列出比例式解答即可．【解答】解：∵AC=4，BC=3，∠C=90°，∴AB==5，当△APQ∽△ABC时，=，即=，解得，AP=；当△APQ∽△ACB时，=，即，解得，AP=，故答案为：或．【点评】本题考查的是相似三角形的性质，掌握相似三角形的对应边的比相等、正确运用分情况讨论思想是解题的关键．17．某货站用传送带传送货物，为了提高传送过程的安全性，工人师傅将原坡角为45°的传送带AB，调整为坡度i=1：的新传送带AC（如图所示）．已知原传送带AB的长是4米．那么新传送带AC的长是8米．【考点】解直角三角形的应用-坡度坡角问题．【分析】根据题意首先得出AD，BD的长，再利用坡角的定义得出DC的长，再结合勾股定理得出答案．【解答】解：过点A作AD⊥CB延长线于点D，∵∠ABD=45°，∴AD=BD，∵AB=4，∴AD=BD=ABsin45°=4×=4，∵坡度i=1：，∴==，则DC=4，故AC==8（m）．故答案为：8．【点评】此题主要考查了勾股定理以及解直角三角形的应用等知识，正确得出DC，AD的长是解题关键．18．已知A（3，2）是平面直角坐标中的一点，点B是x轴负半轴上一动点，联结AB，并以AB为边在x 轴上方作矩形ABCD，且满足BC：AB=1：2，设点C的横坐标是a，如果用含a的代数式表示D点的坐标，那么D点的坐标是（2，）．【考点】相似三角形的判定与性质；坐标与图形性质．【分析】如图，过C作CH⊥x轴于H，过A作AF⊥x轴于F，AG⊥y轴于G，过D作DE⊥AG于E，于是得到∠CHB=∠AFO=∠AED=90°，根据余角的性质得到∠DAE=∠FAB，推出△BCH∽△ABF，根据相似三角形的性质得到，求得BH=AF=1，CH=BF=，通过△BCH≌△ADE，得到AE=BH=1，DE=CH=，求得EG=3﹣1=2，于是得到结论．【解答】解：如图，过C作CH⊥x轴于H，过A作AF⊥x轴于F，AG⊥y轴于G，过D作DE⊥AG于E，∴∠CHB=∠AFO=∠AED=90°，∴∠GAF=90°，∴∠DAE=∠FAB，∵四边形ABCD是矩形，∴∠ABC=90°，∴∠BCH=∠ABF，∴△BCH∽△ABF，∴，∵A（3，2），∴AF=2，AG=3，∵点C的横坐标是a，∴OH=﹣a，∵BC：AB=1：2，∴BH=AF=1，CH=BF=，∵△BCH∽△ABF，∴∠HBC=∠DAE，在△BCH与△ADE中，，∴△BCH≌△ADE，∴AE=BH=1，DE=CH=，∴EG=3﹣1=2，∴D（2，）．故答案为：（2，）．【点评】本题考查了相似三角形的判定和性质，坐标与图形的性质，全等三角形的判定和性质，矩形的性质，正确的画出图形是解题的关键．三、解答题：（本大题共7题，满分78分）19．已知：如图，在梯形ABCD中，AD∥BC，AD=，点M是边BC的中点=，=（1）填空：=，=﹣﹣（结果用、表示）（2）直接在图中画出向量2+．（不要求写作法，但要指出图中表示结论的向量）【考点】*平面向量．【分析】（1）由在梯形ABCD中，AD∥BC，AD=，可求得，然后由点M是边BC的中点，求得，再利用三角形法则求解即可求得；（2）首先过点A作AE∥CD，交BC于点E，易得四边形AECD是平行四边形，即可求得=2，即可知=2+．【解答】解：（1）∵在梯形ABCD中，AD∥BC，AD=，=，∴=3=3，∵点M是边BC的中点，∴==；∴=﹣=﹣（+）=﹣﹣；故答案为：，﹣﹣；（2）过点A作AE∥CD，交BC于点E，∵AD∥BC，∴四边形AECD是平行四边形，∴==，∴=﹣=2，∴=+=2+．【点评】此题考查了平面向量的知识以及平行四边形的性质．注意掌握平行四边形法则与三角形法则的应用是解此题的关键．20．将抛物线y=先向上平移2个单位，再向左平移m（m＞0）个单位，所得新抛物线经过点（﹣1，4），求新抛物线的表达式及新抛物线与y轴交点的坐标．【考点】二次函数图象与几何变换．【分析】利用二次函数平移的性质得出平移后解析式，进而利用x=0时求出新抛物线与y轴交点的坐标．【解答】解：由题意可得：y=（x+m）2+2，代入（﹣1，4），解得：m1=3，m2=﹣1（舍去），故新抛物线的解析式为：y=（x+3）2+2，当x=0时，y=，即与y轴交点坐标为：（0，）．【点评】此题主要考查了二次函数图象与几何变换，正确利用二次函数平移的性质得出解析式是解题关键．21．如图，已知AD是⊙O的直径，AB、BC是⊙O的弦，AD⊥BC，垂足是点E，BC=8，DE=2，求⊙O 的半径长和sin∠BAD的值．【考点】垂径定理；解直角三角形．【分析】设⊙O的半径为r，根据垂径定理求出BE=CE=BC=4，∠AEB=90°，在Rt△OEB中，由勾股定理得出r2=42+（r﹣2）2，求出r．求出AE，在Rt△AEB中，由勾股定理求出AB，解直角三角形求出即可．【解答】解：设⊙O的半径为r，∵直径AD⊥BC，∴BE=CE=BC==4，∠AEB=90°，在Rt△OEB中，由勾股定理得：OB2=0E2+BE2，即r2=42+（r﹣2）2，解得：r=5，即⊙O的半径长为5，∴AE=5+3=8，∵在Rt△AEB中，由勾股定理得：AB==4，∴sin∠BAD===．【点评】本题考查了垂径定理，勾股定理，解直角三角形的应用，能根据垂径定理求出BE是解此题的关键．22．已知：如图，有一块面积等于1200cm2的三角形纸片ABC，已知底边与底边BC上的高的和为100cm （底边BC大于底边上的高），要把它加工成一个正方形纸片，使正方形的一边EF在边BC上，顶点D、G分别在边AB、AC上，求加工成的正方形铁片DEFG的边长．【考点】相似三角形的应用．【分析】作AM⊥BC于M，交DG于N，设BC=acm，BC边上的高为hcm，DG=DE=xcm，根据题意得出方程组求出BC和AM，再由平行线得出△ADG∽△ABC，由相似三角形对应高的比等于相似比得出比例式，即可得出结果．【解答】解：作AM⊥BC于M，交DG于N，如图所示：设BC=acm，BC边上的高为hcm，DG=DE=xcm，根据题意得：，解得：，或（不合题意，舍去），∴BC=60cm，AM=h=40cm，∵DG∥BC，∴△ADG∽△ABC，∴，即，解得：x=24，即加工成的正方形铁片DEFG的边长为24cm．【点评】本题考查了方程组的解法、相似三角形的运用；熟练掌握方程组的解法，证明三角形相似得出比例式是解决问题的关键．23．已知，如图，在四边形ABCD中，∠ADB=∠ACB，延长AD、BC相交于点E．求证：（1）△ACE∽△BDE；（2）BE•DC=AB•DE．【考点】相似三角形的判定与性质．【专题】证明题．【分析】（1）根据邻补角的定义得到∠BDE=∠ACE，即可得到结论；（2）根据相似三角形的性质得到，由于∠E=∠E，得到△ECD∽△EAB，由相似三角形的性质得到，等量代换得到，即可得到结论．【解答】证明：（1）∵∠ADB=∠ACB，∴∠BDE=∠ACE，∴△ACE∽△BDE；（2）∵△ACE∽△BDE，∴，∵∠E=∠E，∴△ECD∽△EAB，∴，∴，∴BE•DC=AB•DE．【点评】本题考查了相似三角形的判定和性质，邻补角的定义，熟练掌握相似三角形的判定和性质是解题的关键．24．已知，如图，在平面直角坐标系xOy中，二次函数y=ax2﹣的图象经过点、A（0，8）、B（6，2）、C（9，m），延长AC交x轴于点D．（1）求这个二次函数的解析式及的m值；（2）求∠ADO的余切值；（3）过点B的直线分别与y轴的正半轴、x轴、线段AD交于点P（点A的上方）、M、Q，使以点P、A、Q为顶点的三角形与△MDQ相似，求此时点P的坐标．【考点】二次函数综合题．【分析】（1）把点A、B的坐标代入函数解析式求得系数a、c的值，从而得到函数解析式，然后把点C的坐标代入来求m的值；（2）由点A、C的坐标求得直线AC的解析式，然后根据直线与坐标轴的交点的求法得到点D的坐标，所以结合锐角三角函数的定义解答即可；（3）根据相似三角形的对应角相等进行解答．【解答】解：（1）把A（0，8）、B（6，2）代入y=ax2﹣，得，解得，故该二次函数解析式为：y=x2﹣x+8．把C（9，m），代入y=x2﹣x+8得到：m=y=×92﹣×9+8=5，即m=5．综上所述，该二次函数解析式为y=x2﹣x+8，m的值是5；（2）由（1）知，点C的坐标为：（9，5），又由点A的坐标为（0，8），所以直线AC的解析式为：y=﹣x+8，令y=0，则0=﹣x+8，解得x=24，即OD=24，所以cot∠ADO===3，即cot∠ADO=3；（3）在△APQ与△MDQ中，∠AQP=∠MQD．要使△APQ与△MDQ相似，则∠APQ=∠MDQ或∠APQ=∠DMQ（根据题意，这种情况不可能），∴cot∠APQ=cot∠MDQ=3．作BH⊥y轴于点H，在直角△PBH中，cot∠P==3，∴PH=18，OP=20，∴点P的坐标是（0，20）．【点评】本题是二次函数的综合题型，其中涉及到的知识点有待定系数法求二次函数、一次函数解析式，相似三角形的判定与性质，锐角三角函数的定义．在求有关动点问题时要注意分析题意分情况讨论结果．25．如图，已知锐角∠MBN的正切值等于3，△PBD中，∠BDP=90°，点D在∠MBN的边BN上，点P 在∠MBN内，PD=3，BD=9，直线l经过点P，并绕点P旋转，交射线BM于点A，交射线DN于点C，设=x（1）求x=2时，点A到BN的距离；（2）设△ABC的面积为y，求y关于x的函数解析式，并写出函数的定义域；（3）当△ABC因l的旋转成为等腰三角形时，求x的值．【考点】几何变换综合题．【分析】（1）由PD∥AH得到=2，即可；（2）由PD∥AH得到，再由tan∠MBN=3，比例式表示出BC，CD，即可；（3）△ABC为等腰三角形时，分三种情况①AB=AC，②CB=CA，③BC=BA利用tan∠MBN=3，建立方程即可．【解答】解：（1）如图1，过点A作AH⊥BC，∵PD⊥BC，∴PD∥AH，∴=2，∴AH=2PD=6，（2）∵PD∥AH，∴=x，∴AH=PD×x=3x，∵tan∠MBN=3，∴BH=3，∵，∴，∴CD=，∴BC=BD+CD=9+=，∴S△ABC=AH×BC=×3x×=，∴y=（1＜x≤9），（3）①当AB=AC时，∵tan∠PCB=tan∠MBC=3，∴=3，∴CD=1，∴BC=BD+CD=10，∴=10，∴x=5，②当CB=CA时，如图2，过点C作CE⊥AB，BE=AB=x，∵tan∠MBN=3，∴cos∠MBN=，∴=，∴，∴x=；③当BA=BC时，x=，∴x=1+，∴△ABC为等腰三角形时，x=5或或1+．【点评】此题是几何变换的综合题，主要考查平行线分线段成比例定理和锐角三角函数，由平行线分线段成比例定理建立方程是解本题的关键．。

2020年上海市普陀区中考语文一模试卷一、文言文阅读（40分）1．（16分）默写。

（1）长风破浪会有时，。

（《行路难》）（2）欲为圣明除弊事，。

（《左迁至蓝关示侄孙湘》）（3），起坐而喧哗者，众宾欢也。

（《醉翁亭记》）（4）所以动心忍性，。

（《生于忧患，死于安乐》）（5）写作时想阐释学习过程中应学思结合，可引用孔子的名言“，。

”2．（12分）阅读下面古诗文，完成下列各题水调歌头明月几时有？把酒问青天。

不知天上宫阙，今夕是何年。

我欲乘风归去，又恐琼楼玉宇，高处不胜寒。

起舞弄清影，何似在人间。

转朱阁，低绮户，照无眠。

不应有恨，何事长向别时圆？人有悲欢离合，月有阴晴圆缺，此事古难全。

但愿人长久，千里共婵娟。

岳阳楼记（节选）至若春和景明，波澜不惊，上下天光，一碧万顷，沙鸥翔集，锦鳞游泳，岸芷汀兰，郁郁青青。

而或长烟一空，皓月千里，浮光跃金，静影沉璧，渔歌互答，此乐何极！登斯楼也，则有心旷神怡，宠辱偕忘，把酒临风，其喜洋洋者矣。

（1）用现代汉语翻译下面的句子。

岸芷汀兰，郁郁青青。

（2）《水调歌头》的作者是，诗人因看到而“把酒问青天”，奇特的想象体现诗人的个性。

（3）《岳阳楼记》中“把酒临风”的意思是，这段抒写了迁客骚人因而“喜洋洋”。

此段描写的作用是。

3．（12分）阅读下文，完成第下列各题苏轼私识范淹庆历三年，轼始总角①，入乡校。

士有自京师来者，以鲁人石守道作《庆历圣德诗》示乡先生②，轼从旁窃．观，则能诵习其词，问先生以所颂十一人者何人也。

先生尽以告之。

且曰：“韩、范、富、欧阳③，此四人者，人杰也。

”时虽未尽了，则已私识之矣。

嘉祜二年，始举．进士，至京师，则范公殁④．既葬，而墓碑出，读之至流涕，曰：“吾得其为人，盖十有五年，而不一见其面，岂非命也欤？”（宋•苏轼《范文正公文集》序，有则改）【注释】①总角：指八九岁到十三四岁的少年。

②乡先生：乡里的私塾先生。

③韩、范、富、欧阳：分别指韩琦、范仲淹、富弼、欧阳修。

普陀区2019学年度第一学期初三质量调研数学试卷（时间：100分钟，满分：150分）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上]1．已知xy35，那么下列等式中，不一定正确的是（▲）（A）5x=3y；（B）x+y8；（C）x+y8y5；（D）x xyy35．2．下列二次函数中，如果函数图像的对称轴是y轴，那么这个函数是（▲）（A）22yxx；（B）221yxx；（C）22yx；（D）2y(x1)．3．已知在Rt△ABC中，C90，sin1A，那么下列说法中正确的是（▲）3（A）1cosB；（B）3cot1A；（C）3tan22A；（D）3cot22B．34．下列说法中，正确的是（▲）（A）如果k0，a是非零向量，那么ka0；（B）如果e是单位向量，那么e1；（C）如果ba，那么ba或ba；（D）已知非零向量a，如果向量b5a，那么a∥b．5．如果二次函数2yxmn的图像如图1所示，y那么一次函数ymxn的图像经过（▲）（A）第一、二、三象限；（B）第一、三、四象限；xO （C）第一、二、四象限；（D）第二、三、四象限．图16．如图2，在Rt△ABC中，ACB90，CDAB，垂足为点D，如果C△ADCC△CDB32，CAD9，那么BC的长是（▲）（A）4；（B）6；（C）213；（D）310．二、填空题：（本大题共12题，每题4分，满分48分）AD图2B7．化简：12(ab)(ab)▲．28．抛物线2y(a2)x在对称轴左侧的部分是上升的，那么a的取值范围是▲．9．已知函数2f(x)3x2x1，如果x2，那么f(x)▲．10．如果抛物线22yaxaxc与x轴的一个交点的坐标是(1,0)，那么与x轴的另一个交点的坐标是▲．11．将二次函数222yxx的图像向下平移m(m0)个单位后，它的顶点恰好落在x 轴上，那么m的值等于▲．12．已知在Rt△ABC中，C90，cot 1B，BC2，那么AC▲．313．如图3，△ABC的中线AD、CE交于点G，点F在边AC上，GF//BC，那么G F BC的值是▲．14．如图4，在△ABC与△AED中，A BBCAEED，要使△ABC与△AED相似，还需添加一个条件，这个条件可以是▲．（只需填一个条件）A AADGEBDC图3 BC图4CD图5B 215．如图5，在Rt△ABC中，C90，AD是三角形的角平分线，如果AB35，AC25，那么点D到直线AB的距离等于▲．16．如图6，斜坡AB长为100米，坡角ABC30，现因“改小坡度”工程的需要，将斜坡AB改造成坡度i1:5的斜坡BD（A、D、C三点在地面的同一条垂线上），那么由点到点下降了▲米．（结果保留根号）ADAAADODB图6 C CB图7BC图817．如图7，在四边形ABCD中，ABC90，对角线AC、BD交于点O，AOCO，CDBD，如果CD3，BC5，那么AB▲．18．如图8，在Rt△ABC中，C90，AC5，sin5B，点P为边BC上一点，PC3，13将△ABC绕点P旋转得到△ABC（点A、B、C分别与点A、B、C对应），使BC //AB，边AC与边AB交于点G，那么AG的长等于▲．三、解答题：（本大题共7题，满分78分）19．（本题满分10分）计算：22sin60cos602tan604cos45．20.（本题满分10分）如图9，在△ABC中，点D、E、F分别在边AB、AC、BC上，DE//BC，EF//AB，AD:AB1:3．（1）当DE5时，求FC的长；（2）设ADa，CFb，那么FE▲，EA▲（用向量a、b表示）．ADEBCF图9 3如图10，在△ABC中，点P、D分别在边BC、AC上，PAAB，垂足为点A，DPBC，垂足为点P，A PBPPDCD．（1）求证：APDC；（2）如果AB3，DC2，求AP的长．ADBPC图10 22．（本题满分10分）y 函数mx与函数yxk（m、k为不等于零的常数）的图像有一个公共点A3,k2，其中正比例函数y的值随x的值增大而减小，求这两个函数的解析式．23．（本题满分12分）已知：如图11，四边形ABCD的对角线AC、BD相交于点O，SS△△．AODBOC（1）求证：D OOBC OOA；CD（2）设△OAB的面积为S，kAB ，求证：2S四边形(k1)S．ABCDDCOAB图11xOy在平面直角坐标系中（如图12），已知抛物线28yax(a)xc(a0)经3过点A3,2，与y轴交于点B0,2，抛物线的顶点为点C，对称轴与x轴交于点D．（1）求抛物线的表达式及点C的坐标；（2）点E是x轴正半轴上的一点，如果AEDBCD，求点E的坐标；（3）在（2）的条件下，点P是位于y轴左侧抛物线上的一点，如果△PAE是以AE为直角边的直角三角形，求点P的坐标．y1O1 x图12如图13，在梯形ABCD中，AD//BC，C90，AD2，BC5，DC3，点E在边BC上，tanAEC3．点M是射线DC上一个动点（不与点D、C重合），联结BM交射线AE于点N，设DMx，ANy．（1）求BE的长；（2）当动点M在线段DC上时，试求y与x之间的函数解析式，并写出函数的定义域；（3）当动点M运动时，直线BM与直线AE的夹角等于45，请直接写出这时线段DM的长．ADMNBEC图13ADBCE6普陀区2019学年度第一学期初三质量调研数学试卷参考答案及评分说明一、选择题：（本大题共6题，每题4分，满分24分）1．(B)；2．(C)；3．(A)；4．(D)；5．(B)；6．(C)．二、填空题：（本大题共12题，每题4分，满分48分）7．a2b；8．a2；9．7；10．(3,0)；11．1；12．6；13．13；14．BE（A BACAEAD等）；15．2；16．50103；17．154；18．2013．三、解答题（本大题共7题，其中第19---22题每题10分，第23、24题每题12分，第25题14分，满分78分）19．解：原式3122()222(3)422···································································（4分）3122 322 ······················································································（3分）322．·····················································································（3分）20．解：（1）∵DE//BC，EF//AB，∴DEBF．···················································································（1分）∵DE5，∴BF5．·····································································（1分）∵DE//BC，∴A DDEABBC．····································∵A DAB13，∴51BC3．···································································（1分）7解得BC15，·················································································（1分）FC10．·······················································································（1分）（2）FE2a，EA1ab．························································（2分+2分）221．解：（1）∵PAAB，DPPC，∴BAPCPD90．····································································（1分）在Rt△ABP与Rt△PCD中，APBPPDCD，∴Rt△ABP∽Rt△PCD．···································································（1分）∴APBPDC．··········································································（1分）∵DPBAPBAPD，DPBPDCC，得APDC．···············································································（2分）（2）∵Rt△ABP∽Rt△PCD．∴BC．∴ABAC．····················································································（1分）∵AB3，DC2，∴AD1．··························································（1分）∵APDC，PADCAP，∴△APD∽△ACP．········································································（1分）∴A DAPAPAC．···············································································（1分）得AP3．····················································································（1分）22．解：由点A3,k2在函数 y x k 的图像上，可得k2 3 k．················································································（1分）整理，得 2230kk ．···································································（1分）解得k 13，k 21．·····································································（2分） ∵正比例函数y 的值随x 的值增大而减小，∴k1．························································································（2分）8得yx ，点A3,3．································································（2分）由点A3,3在函数ym x的图像上，可得m9．···················································································（1分）∴ y9 x ． ····················································································（1分）两个函数的解析式分别为yx ，y9 x． 23．证明：（1）过点A 作AH ⊥BD ，垂足为点H.···················································（1分）1∵S △AOD =DOAH 2 1 ,S△AOB =OBAH2,∴ S S AOD AOB 1 2 1 2DO OB AHAHDO OB .·····························································（2分）SCO同理，BOCSOA AOB．··········································································（1分）∵S S △△， AODBOC∴ D OCO OBOA ．···············································································（1分）（2）∵D OOBC O OA，CODAOB ， ∴△OCD ∽△OAB ．·····································································（1分）∴CDDOCOk ABBOAO．·································································（1分）S S2CDOCD 2．··································································（1分）kABOAB2.·············································（1分） ∵△OAB 的面积为S ，∴S OCD kSSDOAOD，∴SkS又∵kAOD．SOBOAB ···········································（1分）同理，S BOC kS.·····································································（1分）9∴S四边形S△S△S△S△ABCDAOBBOCCODDOAS2kSkS kS(2k2k1)S2(k1)S．·································································（1分）24．解：（1）由抛物线28yax(a)xc经过点A3,2和点B0,2，3c2,8 9a3(a)c2. 3 解得ac4,32.得··············································（2分）∴抛物线的表达式是42yx4x2．3············································（1分）点C的坐标是3(,5)2．··································································（1分）（2）联结AB交CD于点F，过点A作AHOD，H为垂足．∵A3,2，B0,2，∴AB3．由对称性可得3BF．2····································································（1分）∵CD5，∴CF3．在Rt△BCF中，tanBCFBFCF 12 ．·················································（1分）在Rt△AEH中，tan AEH A H EH，∵AEDBCD，∴A HEH12．∴EH4．···································································（1分）∵OH3，∴OE1．∴点E的坐标是1,0．·······································································（1分）（3）∵△PAE是以AE为直角边的直角三角形，∴PAE90或PEA90．设点P点的坐标为42 (m,m4m2)．3①当PAE90时，点P只能在AE的下方．过点P作PGAH，G为垂足．10∴PGm3，42 AGm4m．3∵GAEAHEAEH，GAEPAEPAG，∴PAGAEH．∴tanPAGtanAEH．∴P GAHAGEH．∴m31422m4m3．···················································（1分）解得m3，3 m．2∵m3不合题意舍去，∴3m．2∴点P的坐标是3(,5)2．······························································（1分）②当PEA90时．同理可得点P的坐标是912913129(,)42．··································（2分）25．解：（1）过点A作AHBC，H为垂足．∵AHBC，∴AHE90．∵C90，∴AHEC．∴AH//DC．∵AD//BC，DC3∴AHDC3．·······························································（1分）同理可得HCAD2．··························································································（1分）AH在Rt△AEH中，AHE90，tanAEH3，∴3HE．∴EH1．···············································································································（1分）∵BC5，∴BE2．·····························································································（1分）（2）延长BM、AD交于点G．············································································（1分）∵DG//BC，∴D GDMBCMC．由DMx，DC3，BC5，得D Gx53，解得DGx35xx．·········································································（1分）∴AG 63x3x．·········································································································（1分）∵AG//BC，∴A NAGBNBE．在Rt△AEH中，AHE90，EH1，AH3，11。

2020年上海市普陀区中考化学一模试卷一、选择题1. 属于非金属元素的是（）A. MgB. NaC. AlD. Cl2. 在空气中会造成酸雨的是（）A. O2B. N2C. COD. SO23. 属于纯净物的是（）A. 食盐B. 海水C. 大理石D. 木炭4. 飞艇内可填充的气体是（）A. 氦气B. 氧气C. 空气D. 氮气5. 属于化合物的是（）A. P4B. O2C. SiO2D. C606. CO中氧元素化合价为（）A. −1B. −2C. 0D. +27. 化学方程式书写正确的是（）A. 4P+502P2O5 B. 4Fe+3022Fe2O3 C. Mg+O2MgO D. C+202= 2CO28. 为了让煤炭充分燃烧，方法可行的是（）A. 碾成粉末B. 升高燃烧温度C. 加以湿润D. 加入石灰石9. 在氧气中燃烧产生耀眼白光的是（）A. 铁丝B. 白磷C. 硫粉D. 镁条10. 有关溶液说法错误的是（）A. 具有均一性B. 溶质可能有多种C. 一定为无色透明D. 属于混合物11. 如图所示的实验操作正确的是（）A. 固体加热B. 滴加液体C. 液体振荡D. 读取液体体积12. 水蒸发的过程中，发生变化的是（）A. 物质种类B. 元素种类C. 分子大小D. 分子间的间隔13. 吸水过程中一定发生化学反应的是（）A. 泥沙吸水B. 生石灰吸水C. 活性炭吸水D. 纸巾吸水14. 有关“物质的量”说法正确的是（）A. 属于基本物理量，符号是molB. 物质的量相同则微粒个数相同C. 描述对象一定是微粒D. 物质的量乘以质量等于摩尔质量15. 物质性质和用途关联正确的是（）16. 检验二氧化碳气体是否收集满的方法是（）A. 将带火星的木条伸入集气瓶中B. 将少量澄清石灰水倒入集气瓶中C. 将燃着的木条放在集气瓶口 D. 将pH试纸置于集气瓶口17. 以下1mol物质中所含原子个数最少的是（）A. 铜B. 水C. 氢气D. 二氧化碳18. 下列互为同素异形体的是（）A. 木炭和焦炭B. 白磷和红磷C. 氧化铁和氧化亚铁D. 水和双氧水19. 某温度下一定量的硝酸钾溶液，若将该溶液恒温蒸发掉20g水，溶液恰好达到饱和状态；若在原溶液中加入6g硝酸钾，充分搅拌后，仍有2g不溶解。

2020年上海市普陀区初三一模英语试卷（含答案）（精校Word版）Part 1 Listening（第一部分听力）Part 2 Phonetics, Grammar and Vocabulary（第二部分语音、语法和词汇）Ⅱ. Choose the best answer （选择最恰当的答案）26. Which of the following underlined parts is different in pronunciation from others?A. We should be brave to face the challenge.B. The man was lucky to escape from the fireC. The detective’s work is of great v alue.D. Recycling wastes is better than burning them.27. Garry likes to go for ________ picnic with his family on sunny weekends.A. aB. anC. theD. /28. Jack worked hard and helped us a lot, ________ we selected him as the model student.A. forB. orC. sinceD. so29. We’d better put these tools away________ the time being. They’ll be helpful later.A. onB. inC. atD. for30. ________ wonderful thing it is to explore the city in free time!A. WhatB. What aC. What anD. How a31. ________ of the twin sisters likes the cheese cake because it is too sweet.A. AllB. NeitherC. AnyD. Both32. Ronald started his visit to Canada ________ December 2019.A. withB. onC. inD. of33. Mr. Han has the habit of taking notes on ________ side of the page when he reads.A. anotherB. otherC. othersD. the other34. With a black belt, your blue dress looks much ________ than before.A. beautifulB. more beautifulC. most beautifulD. the most beautiful35. It is hard to make friends with others in a new place ________ we start to talk with them.A. unlessB. whenC. ifD. after36. Terry gets up at 6:30 every morning and then he ________ a bath.A. hasB. haveC. hadD. is having37. David and his younger brother ________ in the station since 1999.A. workB. had workedC. were workingD. have worked38. If you keep ________ five sentences a day, you will be able to speak nice English.A. learnB. to learnC. learningD. learned39. The performance by the funny man made the audience ________ for a long time.A. laughB. to laughC. laughingD. laughed40. Don’t forget ________ some spare batteries when you take photos of these amazing animals.A. takeB. takingC. to takeD. taken41. Kitty ________ the list in her pocket and went out of the room quietly.A. will putB. would putC. putD. has put42. -- ________ will Dad finish cooking the vegetable soup?-- In about 20 minutes.A. How longB. How soonC. How muchD. How far43. The sign says, “Passengers ________ carry matches and knives onto the train.”A. may notB. needn’tC. wouldn’tD. mustn’t44. -- ________. -- I’ve lost my key to the door.A. Is there anything wrong, George?B. What’s your favourite film?C. Let’s go to the concert.D. I’m so sorry for breaking your glass.45. -- I think the Century Park is a good place for camping.-- ________. In my opinion, the National Park is better.A. It’s really a hard job.B. I don’t agree.C. That’s all right.D. Never mind.Ⅲ. Complete the following passage with the words in the box. Each can only be used once （将下列单词填入空格。

2020年上海市普陀区中考数学一模试卷一、选择题（本大题共6小题，共24.0分）1.已知xy =35，那么下列等式中，不一定正确的是()A. 5x=3yB. x+y=8C. x+yy =85D. xy=x+3y+52.下列二次函数中，如果函数图象的对称轴是y轴，那么这个函数是()A. y=x2+2xB. y=x2+2x+1C. y=x2+2D. y=(x−1)223.已知在Rt△ABC中，∠C=90°，sinA=13，那么下列说法中正确的是()A. cosB=13B. cotA=13C. tanA=2√23D. cotB=2√234.下列说法中，正确的是()A. 如果k=0，a⃗是非零向量，那么k a⃗=0B. 如果e⃗是单位向量，那么e⃗=1C. 如果|b⃗ |=|a⃗|，那么b⃗ =a⃗或b⃗ =−a⃗D. 已知非零向量a⃗，如果向量b⃗ =−5a⃗，那么a⃗//b⃗5.如果二次函数y=(x−m)2+n的图象如图所示，那么一次函数y=mx+n的图象经过()A. 第一、二、三象限B. 第一、三、四象限C. 第一、二、四象限D. 第二、三、四象限6.如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为点D，如果C△ADCC△CDB =32，AD=9，那么BC的长是()A. 4B. 6C. 2√13D. 3√10二、填空题（本大题共12小题，共48.0分）7.化简：2(a⃗+12b⃗ )−(a⃗−b⃗ )=______．8.抛物线y=(a−2)x2在对称轴左侧的部分是上升的，那么a的取值范围是______．9.已知函数f(x)=3x2−2x−1，如果x=2，那么f(x)=______．10.如果抛物线y=ax2+2ax+c与x轴的一个交点的坐标是(1,0)，那么与x轴的另一个交点的坐标是______．11.将二次函数y=x2−2x+2的图象向下平移m(m>0)个单位后，它的顶点恰好落在x轴上，那么m的值等于______．12.已知在Rt△ABC中，∠C=90°，cotB=13，BC=2，那么AC=______．13.如图，△ABC的中线AD、CE交于点G，点F在边AC上，GF//BC，那么GFBC的值是______．14.如图，在△ABC与△AED中，ABAE =BCED，要使△ABC与△AED相似，还需添加一个条件，这个条件可以是______(只需填一个条件)．15.如图，在Rt△ABC中，∠C=90°，AD是三角形的角平分线，如果AB=3√5，AC=2√5，那么点D到直线AB的距离等于______．16.如图，斜坡AB长为100米，坡角∠ABC=30°，现因“改小坡度”工程的需要，将斜坡AB改造成坡度i=1：5的斜坡BD(A、D、C三点在地面的同一条垂线上)，那么由点A到点D下降了______米．(结果保留根号)17.如图，在四边形ABCD中，∠ABC=90°，对角线AC、BD交于点O，AO=CO，CD⊥BD，如果CD=3，BC=5，那么AB=______．18.如图，在Rt△ABC中，∠C=90°，AC=5，sinB=513，点P为边BC上一点，PC=3，将△ABC绕点P旋转得到△A′B′C′(点A、B、C分别与点A′、B′、C′对应)，使B′C′//AB，边A′C′与边AB交于点G，那么A′G的长等于______．三、计算题（本大题共1小题，共10.0分） 19. 计算：2sin 260°−cos60°tan 260∘−4cos45∘．四、解答题（本大题共6小题，共68.0分）20. 如图，在△ABC 中，点D 、E 、F 分别在边AB 、AC 、BC 上，DE//BC ，EF//AB ，AD ：AB =1：3． (1)当DE =5时，求FC 的长；(2)设AD ⃗⃗⃗⃗⃗⃗ =a ⃗ ，CF⃗⃗⃗⃗⃗ =b ⃗ ，那么FE ⃗⃗⃗⃗⃗ =______，EA ⃗⃗⃗⃗⃗ =______(用向量a ⃗ ，b ⃗ 表示)．21. 如图，在△ABC 中，点P 、D 分别在边BC 、AC 上，PA ⊥AB ，垂足为点A ，DP ⊥BC ，垂足为点P ，APPD =BPCD ．(1)求证：∠APD =∠C ；(2)如果AB =3，DC =2，求AP 的长．22.函数y=mx 与函数y=xk(m、k为不等于零的常数)的图象有一个公共点A(3,k−2)，其中正比例函数y的值随x的值增大而减小，求这两个函数的解析式．23.已知：如图，四边形ABCD的对角线AC、BD相交于点O，S△AOD=S△BOC．(1)求证：DOOB =COOA；(2)设△OAB的面积为S，CDAB=k，求证：S四边形ABCD=(k+1)2S.24.在平面直角坐标系xOy中(如图)，已知抛物线y=ax2+(a+83)x+c(a≠0)经过点A(−3,−2)，与y轴交于点B(0,−2)，抛物线的顶点为点C，对称轴与x轴交于点D．(1)求抛物线的表达式及点C的坐标；(2)点E是x轴正半轴上的一点，如果∠AED=∠BCD，求点E的坐标；(3)在(2)的条件下，点P是位于y轴左侧抛物线上的一点，如果△PAE是以AE为直角边的直角三角形，求点P的坐标．25.如图，在梯形ABCD中，AD//BC，∠C=90°，AD=2，BC=5，DC=3，点E在边BC上，tan∠AEC=3，点M是射线DC上一个动点(不与点D、C重合)，联结BM交射线AE于点N，设DM=x，AN=y．(1)求BE的长；(2)当动点M在线段DC上时，试求y与x之间的函数解析式，并写出函数的定义域；(3)当动点M运动时，直线BM与直线AE的夹角等于45°，请直接写出这时线段DM的长．答案和解析1.【答案】B【解析】解：A、由比例的性质得到3y=5x，故本选项不符合题意．B、根据比例的性质得到x+y=8k(k是正整数)，故本选项符合题意．C、根据合比性质得到x+yy =85，故本选项不符合题意．D、根据等比性质得到xy =x+3y+5，故本选项不符合题意．故选：B．根据比例的性质作答．考查了比例的性质，需要掌握内项之积等于外项之积、合比性质和等比性质．2.【答案】C【解析】解：二次函数的对称轴为y轴，则函数对称轴为x=0，即函数解析式y=ax2+bx+c中，b=0，故选：C．由已知可知对称轴为x=0，从而确定函数解析式y=ax2+bx+c中，b=0，由选项入手即可．本题考查二次函数的性质；熟练掌握二次函数的图象及性质是解题的关键．3.【答案】A【解析】解：在Rt△ABC中，∠C=90°，sinA=13，则cosA=√1−sin2A=√1−19=2√23A、cosB=sinA=13，故本选项符合题意．B、cotA=cosAsinA =2√2313=2√2.故本选项不符合题意．C、tanA=sinAcosA =132√23=√24.故本选项不符合题意．D、cotB=tanA=√24.故本选项不符合题意．故选：A．利用同角三角函数的关系解答．本题考查同角三角函数关系，(1)平方关系：sin2A+cos2A=1；(2)正余弦与正切之间的关系(积的关系)：一个角的正切值等于这个角的正弦与余弦的比，即tanA=sinAcosA或sinA=tanA⋅cosA．4.【答案】D【解析】解：A、如果k=0，a⃗是非零向量，那么k a⃗=0，错误，应该是k a⃗=0⃗．B、如果e⃗是单位向量，那么e⃗=1，错误．应该是|e⃗|=1．C、如果|b⃗ |=|a⃗|，那么b⃗ =a⃗或b⃗ =−a⃗，错误．模相等的向量，不一定平行．D、已知非零向量a⃗，如果向量b⃗ =−5a⃗，那么a⃗//b⃗ ，正确．故选：D．根据平面向量的性质一一判断即可．本题考查平面向量，平行向量等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．5.【答案】B【解析】解：根据题意得：抛物线的顶点坐标为(m,n)，且在第四象限，∴m>0，n<0，则一次函数y=mx+n经过第一、三、四象限．故选：B．由二次函数解析式表示出顶点坐标，根据图形得到顶点在第四象限，求出m与n的正负，即可作出判断．此题考查了二次函数与一次函数图象与系数的关系，熟练掌握二次函数及一次函数的图象与性质是解本题的关键．6.【答案】C【解析】解：∵∠ACB=90°，∴∠ACD+∠BCD=90°，∵CD⊥AB，∴∠A+∠ACD=90°，∴∠A=∠BCD，又∠ADC=∠CDB，∴△ADC∽△CDB，∴ADCD =CDBD，C△ADCC△CDB=ADCD，∴ADCD =32，即9CD=32，解得，CD=6，∴96=6BD，解得，BD=4，∴BC=√CD2+BD2=√62+42=2√13，故选：C．证明△ADC∽△CDB，根据相似三角形的性质求出CD、BD，根据勾股定理求出BC．本题考查的是相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理是解题的关键．7.【答案】a⃗+2b⃗【解析】解：2(a⃗+12b⃗ )−(a⃗−b⃗ )=2a⃗+b⃗ −a⃗+b⃗ =a⃗+2b⃗ ．故答案为：a⃗+2b⃗ ．直接利用向量加减运算法则去括号合并求出答案．此题主要考查了平面向量，正确掌握运算法则是解题关键．8.【答案】a<2【解析】解：∵抛物线y=(a−2)x2在对称轴左侧的部分是上升的，∴抛物线开口向下，∴a−2<0，解得a<2．故答案为a<2．利用二次函数的性质得到抛物线开口向下，则a−2<0，然后解不等式即可．本题考查了二次函数图象与系数的关系：二次项系数a决定抛物线的开口方向和大小．当a>0时，抛物线向上开口；当a<0时，抛物线向下开口．9.【答案】7【解析】解：f(2)=3×22−2×2−1=7，故答案为7．把x=2代入函数关系式即可求得．本题考查了二次函数图象上点的坐标特征，函数图象上点的坐标适合解析式．10.【答案】(−3,0)【解析】解：∵抛物线y=ax2+2ax+c=a(x+1)2−a+c，∴该抛物线的对称轴是直线x=−1，∵抛物线y=ax2+2ax+c与x轴的一个交点的坐标是(1,0)，∴该抛物线与x轴的另一个交点的坐标是(−3,0)，故答案为：(−3,0)．根据抛物线y=ax2+2ax+c，可以得到该抛物线的对称轴，然后根据二次函数图象具有对称性和抛物线y=ax2+2ax+c与x轴的一个交点的坐标是(1,0)，可以得到该抛物线与x轴的另一个交点坐标．本题考查抛物线与x轴的交点，解答本题的关键是明确题意，利用二次函数的性质解答．11.【答案】1【解析】解：y=x2−2x+2=(x−1)2+1，∴将抛物线y=x2−2x+2沿y轴向下平移1个单位，使平移后的抛物线的顶点恰好落在x轴上，∴m=1，故答案为：1．利用平移的性质得出平移后解析式，进而得出其顶点坐标，再代入直线y=0求出即可．此题主要考查了二次函数的平移以及图形的旋转以及配方法求二次函数顶点坐标等知识，正确记忆二次函数平移规律是解题关键．12.【答案】6【解析】解：∵cotB=BCAC，∴AC=BCcotB =BC13=3BC=6．故答案是：6．根据三角函数的定义即可求解．本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边，余切为邻边比对边．13.【答案】13【解析】解：∵△ABC的中线AD、CE交于点G，∴G是△ABC的重心，∴AGGD =21，∵GF//BC，∴GFDC =AGAD=23，∵DC=12BC，∴GFBC =13，故答案为：13根据三角形的重心和相似三角形的判定和性质解答即可．此题考查三角形重心问题，关键是根据三角形的重心得出比例关系．14.【答案】∠E=∠B(答案不唯一)【解析】解：添加条件：∠B=∠E；∵ABAE =BCED，∠B=∠E，∴△ABC∽△AED，故答案为：∠B=∠E(答案不唯一)．根据两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似可得添加条件：∠B=∠E．此题主要考查了相似三角形的判定，关键是掌握相似三角形的判定定理．15.【答案】2【解析】解：作DE⊥AB于E，如图，在Rt△ABC中，BC=√(3√5)2−(2√5)2=5，∵AD是三角形的角平分线，DE⊥AB，∠C=90°，∴DC=DE，∵S△ACD+S△ABD=S△ABC，∴12×2√5×DC+12×DE×3√5=12×2√5×5，∴DE=2，即点D到直线AB的距离等于2．故答案为2．作DE⊥AB于E，如图，利用勾股定理计算出BC=5，再根据角平分线的性质得DC=DE，然后利用面积法得到12×2√5×DC+12×DE×3√5=12×2√5×5，从而可求出DE．本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．16.【答案】(50−10√3)【解析】解：在Rt△ABC中，∠ABC=30°，∴AC=12AB=50米，BC=AB⋅cso∠ABC=50√3米，∵斜坡BD的坡度i=1：5，∴DC：BC=1：5，∴DC=10√3米，则AD=(50−10√3)米，故答案为：(50−10√3).根据直角三角形的性质求出AC，根据余弦的定义求出BC，根据坡度的概念求出CD，结合图形计算，得到答案．本题考查的是解直角三角形的应用−坡度坡角问题，掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键．17.【答案】154【解析】【分析】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，勾股定理等知识，添加恰当辅助线构造全等三角形和相似三角形是本题的关键．过点A作AE⊥BD，由“AAS”可证△AOE≌△COD，可得CD=AE=3，由勾股定理可求BD=4，通过证明△ABE∽△BCD，可得AEBD =ABBC，即可求解．【解答】解：如图，过点A作AE⊥BD，∵CD⊥BD，AE⊥BD，∴∠CDB=∠AED=90°，且CO=AO，∠COD=∠AOE，∴△AOE≌△COD(AAS)∴CD=AE=3，∵∠CDB=90°，BC=5，CD=3，∴DB=√BC2−CD2=√25−9=4；∵∠ABC=∠AEB=90°，∴∠ABE+∠EAB=90°，∠CBD+∠ABE=90°，∴∠EAB=∠CBD，且∠CDB=∠AED=90°，∴△ABE∽△BCD，∴AEBD =ABBC，∴34=AB5∴AB=154故答案为：154．18.【答案】2013【解析】解：如图，作PH⊥AB于H．在Rt△ABC中，∠C=90°，AC=5，sinB=513，∴ACAB =513，∴AB=13，BC=√AB2−AC2=√132−52=12，∵PC=3，∴PB=9，∵∠BPH∽△BAC，∴PHAC =PBAB，∴PH5=913，∴PH=4513，∵AB//B′C′，∴∠HGC′=∠C′=∠PHG=90°，∴四边形PHGC′是矩形，∴CG′=PH=4513，∴A′G=5−4513=2013，故答案为2013．如图，作PH⊥AB于H.利用相似三角形的性质求出PH，再证明四边形PHGC′是矩形即可解决问题．本题考查旋转变换，平行线的性质，解直角三角形等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．19.【答案】解：原式=2×(√32 )2−12(√3)2−4×√22=32−123−2√2=13−2√2=3+2√2．【解析】本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．根据特殊角三角函数值，可得实数的运算，根据实数的运算，可得答案．20.【答案】解：(1)∵DE//BC ，EF//AB ，∴四边形DEFB 是平行四边形，∴DE =BF =5，∵AD ：AB =DE ：BC =1：3，∴BC =15，∴CF =BC −BF =15−5=10；(2)−2a ⃗ ；12b ⃗−a ⃗ ．【解析】【分析】本题考查平面向量，平行向量等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．(1)利用平行线分线段成比例定理求解即可．(2)利用三角形法则求解即可．【解答】解：(1)见答案；(2)∵AD ：AB =1：3，∴DB ⃗⃗⃗⃗⃗⃗ =2AD ⃗⃗⃗⃗⃗⃗ =2a ⃗ ，∵EF =BD ，EF//BD ，∴FE ⃗⃗⃗⃗⃗ =−DB ⃗⃗⃗⃗⃗⃗ =−2a ⃗ ，∵CF =2DE ，∴ED ⃗⃗⃗⃗⃗ =12CF ⃗⃗⃗⃗⃗ =12b ⃗ ， ∴EA ⃗⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ +DA ⃗⃗⃗⃗⃗ =12b ⃗ −a ⃗ ， 故答案为−2a⃗ ；12b ⃗ −a ⃗ ． 21.【答案】证明：(1)∵PA ⊥AB ，DP ⊥BC ， ∴∠BAP =∠DPC =90°，∵AP PD =BP CD∴AP BP =PD CD ，∴Rt △ABP∽Rt △PCD ，∴∠B=∠C，∠APB=∠CDP，∵∠DPB=∠C+∠CDP=∠APB+∠APD，∴∠APD=∠C；(2)∵∠B=∠C，∴AB=AC=3，且CD=2，∴AD=1，∵∠APD=∠C，∠CAP=∠PAD，∴△APC∽△ADP，∴APAC=ADAP∴AP2=1×3=3∴AP=√3．【解析】本题考查了相似三角形的判定和性质，等腰三角形的性质，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．(1)通过证明Rt△ABP∽Rt△PCD，可得∠B=∠C，∠APB=∠CDP，由外角性质可得结论；(2)通过证明△APC∽△ADP，可得APAC =ADAP，即可求解．22.【答案】解：根据题意可得3k=k−2，整理得k2−2k+3=0，解得k1=−1，k2=3，∵正比例函数y的值随x的值增大而减小，∴k=−1，∴点A的坐标为(3,−3)，∴反比例函数是解析式为：y=−9x；正比例函数的解析式为：y=−x．【解析】把点A(3,k−2)代入y=xk ，即可得出3k=k−2，据此求出k的值，再根据正比例函数y的值随x的值增大而减小，得出满足条件的k值即可求解．此题考查了反比例函数与一次函数的交点问题，将函数图象的交点与方程(组)的解结合起来是解此类题目常用的方法．23.【答案】证明：(1)∵S△AOD=S△BOC，∴S△AOD+S△AOB=S△BOC+S△AOB，即S△ADB=S△ACB，∴CD//AB，∴△DOC∽△BOA，∴DOOB =COOA；(2)∵△DOC∽△BOA∴CDAB =DOBO=COAO=k，S△CODS△AOB=(CDAB)2=k2，∴DO=kOB，CO=kAO，S△COD=k2S，∴S△AOD=kS△OAB=kS，S△COB=kS△OAB=kS，∴S四边形ABCD=S+kS+kS+k2S=(k+1)2S.【解析】本题考查了相似三角形的判定和性质，证明△DOC∽△BOA是本题的关键．(1)由S△AOD=S△BOC易得S△ADB=S△ACB，根据三角形面积公式得到点D和点C到AB的距离相等，则CD//AB，于是可判断△DOC∽△BOA，然后利用相似比即可得到结论；(2)利用相似三角形的性质可得结论．24.【答案】解：(1)将点A(−3,−2)、B(0,−2)代入抛物线y=ax2+(a+83)x+c，得，{−2=9a−3(a+83)+c −2=c，解得，a=43，c=−2，∴y=43x2+4x−2=43(x+32)2−5，∴抛物线解析式为y=43x2+4x−2，顶点C的坐标为(−32,−5)；(2)如图1，连接AB，交对称轴于点N，则N(−32,−2)，在Rt△BCN中，tan∠BCN=BNCN =323=12，∴tan∠AED=12，过点A作AH⊥DE于H，则tan∠AED=AHEH =2EH=12，∴EH=4，∴OE=1，∴E(1,0)；(3)①如图2，当∠EAP=90°时，∵∠HEA+∠HAE=90，∠HAE+∠MAP=90°，∴∠HEA=∠MAP，又∠AHE=∠PMA=90°，∴△AHE∽△PMA，则MPAM =AHHE，设PM=t，则AM=2t，将P(t−3,−2−2t)代入y=43x2+4x−2，得，t1=0(舍去)，t2=32，∴P1(−32,−5)；②如图3，当∠AEP=90°时，∵∠EAG+∠AEG=90°，∠AEG+∠PEN=90°，∴∠AEG=∠EPN，又∵∠N=∠G，∴△AEG∽△PEN，则PNEN =EGAG=12，设PN=t，则EN=2t，将P(1−t,2t)代入y=43x2+4x−2，得，t1=13+√1294，t2=13−√1294(舍)，∴P2(−9+√1294,13+√1292)；综上所述：P1(−32,−5)，P2(−9+√1294,13+√1292).【解析】本题考查了待定系数法求解析式，锐角三角形函数，直角三角形的存在性等，解题关键是能够作出适当的辅助线构造相似三角形，并注意分类讨论思想的运用．(1)将点A、B代入抛物线y=ax2+(a+83)x+c，即可求出抛物线解析式，再化为顶点式即可；(2)如图1，连接AB，交对称轴于点N，则N(−32,−2)，利用相等角的正切值相等即可求出EH的长，OE的长，可写出点E的坐标；(3)分∠EAP=90°和∠AEP=90°两种情况讨论，通过相似的性质，用含t的代数式表示出点P的坐标，可分别求出点P的坐标．25.【答案】解：(1)如图1中，作AH⊥BC于H，∵AD//BC，∠C=90°，∴∠AHC=∠C=∠D=90°，∴四边形AHCD是矩形，∴AD=CH=2，AH=CD=3，∵tan∠AEC=3，∴AHEH=3，∴EH=1，CE=1+2=3，∴BE=BC−CE=5−3=2．(2)延长AD交BM的延长线于G．∵AG//BC，∴DGBC =DMCM，∴DG5=x3−x，∴DG=5x3−x ，AG=2+5x3−x=6+3x3−x，∵ANNE =AGBE，∴y√10−y =6+3x3−x2，∴y=3√10x+6√10x+12(0<x<3)．(3)①如图3−1中，当点M在线段DC上时，∠BNE=∠ABC=45°，∵△EBN∽△EAB，∴EB2=EN⋅AE，∴4=2√10(3−x)12+x⋅√10，解得x=12．②如图3−2中，当点M在线段DC的延长线上时，∠ANB=∠ABE=45°，∵△BNA∽△EBA，∴AB2=AE⋅AN，∴(3√2)2=√10⋅[√10+2√10(x−3) 12+x解得x=13，综上所述DM的长为1或13．2【解析】本题考查四边形综合题，考查了相似三角形的判定和性质，矩形的判定和性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．(1)如图1中，作AH⊥BC于H，解直角三角形求出EH，CH即可解决问题．(2)延长AD交BM的延长线于G.利用平行线分线段成比例定理构建关系式即可解决问题．(3)分两种情形：①如图3−1中，当点M在线段DC上时，∠BNE=∠ABC=45°.②如图3−2中，当点M在线段DC的延长线上时，∠ANB=∠ABE=45°，利用相似三角形的性质即可解决问题．。

普陀区2019学年度第一学期初三质量调研数 学 试 卷（时间：100分钟，满分：150分）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上] 1．已知35x y =，那么下列等式中，不一定正确的是（ ▲ ） （A ）5=3x y ； （B ）+8x y =； （C ）+85x y y =； （D ）35x x y y +=+． 2．下列二次函数中，如果函数图像的对称轴是y 轴，那么这个函数是（ ▲ ）（A ）22y x x =+； （B ）221y x x =++； （C ）22y x =+； （D ）2(1)y x =-． 3．已知在Rt △ABC 中，90C ∠=︒，1sin 3A =，那么下列说法中正确的是（ ▲ ） （A ）1cos 3B =； （B ）1cot 3A =； （C）tan A =； （D）cot B = 4．下列说法中，正确的是（ ▲ ）（A ）如果，a 是非零向量，那么0ka =； （B ）如果e 是单位向量，那么1e =； （C ）如果b a =，那么b a =或b a =-；（D ）已知非零向量a ，如果向量5b a =-，那么a ∥b ．0k =5．如果二次函数()2y x m n =-+的图像如图1所示，那么一次函数y mx n =+的图像经过（ ▲ ） （A ）第一、二、三象限； （B ）第一、三、四象限； （C ）第一、二、四象限； （D ）第二、三、四象限．6．如图2，在Rt △中，90ACB ∠=︒，CD AB ⊥，垂足为点D ，如果32ADC CDB C C =△△，9AD =，那么BC 的长是（ ▲ ）（A ）4； （B ）6； （C） （D）．二、填空题：（本大题共12题，每题4分，满分48分） 7．化简：12()()2a b a b →→→→+--= ▲ ． 8．抛物线2(2)y a x =-在对称轴左侧的部分是上升的，那么a 的取值范围是 ▲ ． 9．已知函数2()321f x x x =--，如果2x =，那么()f x = ▲ ．10．如果抛物线22y ax ax c =++与x 轴的一个交点的坐标是(1,0)，那么与x 轴的另一个交点的坐标是 ▲ ．11．将二次函数222y x x =-+的图像向下平移m (0)m >个单位后，它的顶点恰好落在x轴上，那么m 的值等于 ▲ ．12．已知在Rt △ABC 中，90C ∠=︒，1cot 3B =，2BC =，那么AC = ▲ ．13．如图3，△ABC 的中线AD 、CE 交于点G ，点F 在边AC 上，GF //BC ，那么GFBC的值是 ▲ ．14．如图4，在△ABC 与△AED 中，AB BCAE ED=，要使△ABC 与△AED 相似，还需添加 一个条件，这个条件可以是 ▲ ．（只需填一个条件）ABC 图 3ABCDEG F图2AD CB图5ABCD 图4ABCEDO图115． 如图5，在Rt △中，90C ∠=︒，AD 是三角形的角平分线，如果AB =AC =那么点D 到直线AB 的距离等于 ▲ ．16．如图6，斜坡AB 长为100米，坡角30ABC ∠=︒，现因“改小坡度”工程的需要，将斜坡AB 改造成坡度1:5i =的斜坡BD （、、C 三点在地面的同一条垂线上），那么由点到点下降了 ▲ 米．（结果保留根号）17．如图7，在四边形ABCD 中，90ABC ∠=︒，对角线AC 、BD 交于点O ，AO CO =，CD BD ⊥，如果3CD =，5BC =，那么AB = ▲ ．18．如图8，在Rt △ABC 中，90C ∠=︒，5AC =，5sin 13B =，点P 为边BC 上一点，3PC =， 将△ABC 绕点P 旋转得到△A B C '''（点A 、B 、C 分别与点A '、B '、C '对应），使B C ''//AB ，边A C ''与边AB 交于点G ，那么A G '的长等于 ▲ ． 三、解答题：（本大题共7题，满分78分）19．（本题满分10分）计算：222sin 60cos60tan 604cos45︒-︒︒-︒．20.（本题满分10分）如图9，在△ABC 中，点D 、E 、F 分别在边AB 、AC 、BC 上，DE //BC ，EF //AB ，:1:3AD AB =．（1）当5DE =时，求FC 的长；（2）设AD a =，CF b =，那么FE = ▲ ，EA = ▲ （用向量a 、b 表示）．ABC A D A DABDE F图9图8ABC图7ADC BOAD B图6C如图10，在△ABC 中，点P 、D 分别在边BC 、AC 上，PA AB ⊥，垂足为点A ，DP BC ⊥，垂足为点P ，AP BPPD CD=． （1）求证：APD C ∠=∠；（2）如果3AB =，2DC =，求AP 的长．22．（本题满分10分）函数m y x =与函数xy k=（m 、k 为不等于零的常数）的图像有一个公共点()3,2A k -，其中正比例函数y 的值随x 的值增大而减小，求这两个函数的解析式．23．（本题满分12分）已知：如图11，四边形ABCD 的对角线AC 、BD 相交于点O ，AOD BOC S S =△△． （1）求证：OACOOB DO =； （2）设△OAB 的面积为S ，k ABCD=，求证：2(1)ABCD S k S =+四边形．CDBAO图11图10CDBAP在平面直角坐标系中（如图12），已知抛物线28()3y ax a x c =+++(0)a ≠经过点A ()3,2--，与y 轴交于点B ()0,2-，抛物线的顶点为点C ，对称轴与x 轴交于点D ．（1）求抛物线的表达式及点C 的坐标；（2）点E 是x 轴正半轴上的一点，如果AED BCD ∠=∠，求点E 的坐标；（3）在（2）的条件下，点P 是位于y 轴左侧抛物线上的一点，如果△PAE 是以AE 为直角边的直角三角形，求点P 的坐标．xOy 图12O11如图13，在梯形ABCD 中，AD //BC ，90C ∠=︒，2AD =，5BC =，3DC =，点E 在边BC 上，tan 3AEC ∠=．点M 是射线DC 上一个动点（不与点D 、C 重合），联结BM 交射线AE 于点N ，设DM x =，AN y =． （1）求BE 的长；（2）当动点M 在线段DC 上时，试求y 与x 之间的函数解析式，并写出函数的定义域； （3）当动点M 运动时，直线BM 与直线AE 的夹角等于45︒，请直接写出这时线段DM 的长．备用图ABCD ENM图13AB CDE普陀区2019学年度第一学期初三质量调研数学试卷参考答案及评分说明一、选择题：（本大题共6题，每题4分，满分24分）1．(B)； 2．(C)； 3．(A)； 4．(D)； 5．(B)； 6．(C)．二、填空题：（本大题共12题，每题4分，满分48分）三、解答题（本大题共7题，其中第19---22题每题10分，第23、24题每题12分，第25题14分，满分78分）19．解：原式212⨯-= ··································································· （4分）31-=······················································································· （3分）3=+ ······················································································ （3分）20．解：（1）∵DE //BC ，EF //AB ，∴DE BF =． ··················································································· （1分） ∵5DE =，∴5BF =． ······································································ （1分） ∵DE //BC ，∴AD DEAB BC =． ·················································································· （1分） ∵13AD AB =，∴513BC =． ···································································· （1分） 解得 15BC =， ················································································ （1分）7． 2a b →→+； 8． 2a <； 9． 7； 10．30-(,) ；11．1； 12．6；13． 13；14．B E ∠=∠（AB ACAE AD=等）； 15．2 ； 16．50- 17．154； 18．2013．10FC =． ························································································ （1分） （2）FE =2a -，EA =12a b -+． ······················································· （2分+2分）21．解：（1）∵PA AB ⊥，DP PC ⊥，∴90BAP CPD ∠=∠=︒． ··································································· （1分） 在Rt △ABP 与Rt △PCD 中，AP BPPD CD=， ∴Rt △ABP ∽Rt △PCD ． ·································································· （1分） ∴APB PDC ∠=∠． ··········································································· （1分） ∵DPB APB APD ∠=∠+∠，DPB PDC C ∠=∠+∠，得APD C ∠=∠． ··············································································· （2分） （2）∵Rt △ABP ∽Rt △PCD ． ∴B C ∠=∠．∴AB AC =． ··················································································· （1分） ∵3AB =，2DC =，∴1AD =． ························································· （1分） ∵APD C ∠=∠，PAD CAP ∠=∠，∴△APD ∽△ACP ． ········································································ （1分） ∴AD APAP AC=． ················································································ （1分）得AP ···················································································· （1分）22．解：由点A ()3,2k -在函数xy k=的图像上，可得 32k k-=．················································································ （1分） 整理，得2230k k --=． ·································································· （1分） 解得 13k =，21k =-． ····································································· （2分） ∵正比例函数y 的值随x 的值增大而减小，∴1k =-． ······················································································· （2分） 得 y x =-，点A ()3,3-． ································································· （2分）由点A ()3,3-在函数my x=的图像上，可得 9m =-． ·················································································· （1分） ∴9y x=-． ····················································································· （1分） 两个函数的解析式分别为y x =-，9y x=-．23．证明：（1）过点A 作AH ⊥BD ，垂足为点H . ···················································· （1分）∵S △AOD =AH DO ⋅⋅21, S △AOB =AH OB ⋅⋅21, ∴OB DO AH OB AHDO S S AOBAOD =⋅⋅⋅⋅=∆∆2121.····························································· （2分） 同理，BOC AOB S COS OA∆∆=． ········································································· （1分） ∵AOD BOC S S =△△，∴DO COOB OA=．··············································································· （1分）（2）∵OACOOB DO =，AOB COD ∠=∠， ∴△OCD ∽△OAB ． ····································································· （1分） ∴CD DO COk AB BO AO===． ·································································· （1分） 22k AB CD S S OAB OCD =⎪⎭⎫ ⎝⎛=∆∆． ·································································· （1分） ∵△OAB 的面积为S ，∴S k S OCD ⋅=∆2. ············································ （1分） 又∵k OBDOS S OAB AOD ==∆∆，∴S k S AOD ⋅=∆． ············································ （1分） 同理，S k S BOC ⋅=∆. ······································································ （1分） ∴AOB BOC COD DOA ABCD S S S S S =+++△△△△四边形S k S k S k S ⋅+⋅+⋅+=2 S k k ⋅++=)12(2S k 2)1(+=． ································································ （1分）24．解：（1）由抛物线28()3y ax a x c =+++经过点A ()3,2--和点B ()0,2-，得2,893() 2.3c a a c =-⎧⎪⎨-++=-⎪⎩ 解得4,32.a c ⎧=⎪⎨⎪=-⎩ ··············································· （2分） ∴抛物线的表达式是24423y x x =+-．············································· （1分） 点C 的坐标是3(,5)2--． ··································································· （1分）（2）联结AB 交CD 于点F ，过点A 作AH OD ⊥，H 为垂足．∵A ()3,2--，B ()0,2-，∴3AB =． 由对称性可得 32BF =． ····································································· （1分） ∵5CD =，∴3CF =．在Rt △BCF 中，1tan 2BF BCF CF ∠==．················································· （1分） 在Rt △AEH 中，tan AHAEH EH∠=，∵AED BCD ∠=∠， ∴12AH EH =．∴4EH =．···································································· （1分） ∵3OH =，∴1OE =．∴点E 的坐标是()1,0． ······································································ （1分） （3）∵△PAE 是以AE 为直角边的直角三角形， ∴90PAE ∠=︒或90PEA ∠=︒．设点P 点的坐标为24(,42)3m m m +-．①当90PAE ∠=︒时，点P 只能在AE 的下方． 过点P 作PG AH ⊥，G 为垂足．∴3PG m =+，2443AG m m =--．∵GAE AHE AEH ∠=∠+∠，GAE PAE PAG ∠=∠+∠，∴PAG AEH ∠=∠．∴tan tan PAG AEH ∠=∠． ∴PG AH AG EH =．∴2314243m m m +=--．··················································· （1分） 解得3m =-，32m =-． ∵3m =-不合题意舍去，∴32m =-． ∴点P 的坐标是3(,5)2--． ······························································· （1分） ②当90PEA ∠=︒时．同理可得点P的坐标是． ··································· （2分）25．解：（1）过点A 作AH BC ⊥，H 为垂足．∵AH BC ⊥，∴90AHE ∠=︒．∵90C ∠=︒，∴AHE C ∠=∠．∴AH //DC ．∵AD //BC ，3DC =∴3AH DC ==． ·······························································（1分） 同理可得2HC AD ==． ····························································································（1分） 在Rt △AEH 中，90AHE ∠=︒，tan 3AEH ∠=，∴3AH HE=． ∴1EH =． ················································································································（1分） ∵5BC =，∴2BE =． ·····························································································（1分）（2）延长BM 、AD 交于点G ． ·············································································（1分） ∵DG //BC ，∴DG DM BC MC=． 由DM x =，3DC =，5BC =， 得53DG x x =-，解得53x DG x=-．···········································································（1分） ∴633x AG x+=-． ·········································································································（1分） ∵AG //BC ，∴AN AG BN BE =． 在Rt △AEH 中，90AHE ∠=︒，1EH =，3AH =，可得AE =． ··········································································································（1分）。

2020年上海市普陀区中考数学一模试卷学校:________ 班级:________ 姓名:________ 学号:________一、单选题（共6小题）1.已知＝，那么下列等式中，不一定正确的是（）A．5x＝3y B．x+y＝8 C．＝D．＝2.下列二次函数中，如果函数图象的对称轴是y轴，那么这个函数是（）A．y＝x2+2x B．y＝x2+2x+1 C．y＝x2+2 D．y＝（x﹣1）223.已知在Rt△ABC中，∠C＝90°，sin A＝，那么下列说法中正确的是（）A．cos B＝B．cot A＝C．tan A＝D．cot B＝4.下列说法中，正确的是（）A．如果k＝0，是非零向量，那么k＝0B．如果是单位向量，那么＝1C．如果||＝||，那么＝或＝﹣D．已知非零向量，如果向量＝﹣5，那么∥5.如果二次函数y＝（x﹣m）2+n的图象如图所示，那么一次函数y＝mx+n的图象经过（）A．第一、二、三象限B．第一、三、四象限C．第一、二、四象限D．第二、三、四象限6.如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为点D，如果＝，AD＝9，那么BC的长是（）A．4 B．6 C．2D．3二、填空题（共12小题）7.化简：2（+）﹣（﹣）＝．8.抛物线y＝（a﹣2）x2在对称轴左侧的部分是上升的，那么a的取值范围是．9.已知函数f（x）＝3x2﹣2x﹣1，如果x＝2，那么f（x）＝．10.如果抛物线y＝ax2+2ax+c与x轴的一个交点的坐标是（1，0），那么与x轴的另一个交点的坐标是﹣．11.将二次函数y＝x2﹣2x+2的图象向下平移m（m＞0）个单位后，它的顶点恰好落在x轴上，那么m的值等于．12.已知在Rt△ABC中，∠C＝90°，cot B＝，BC＝2，那么AC＝．13.如图，△ABC的中线AD、CE交于点G，点F在边AC上，GF∥BC，那么的值是．14.如图，在△ABC与△AED中，＝，要使△ABC与△AED相似，还需添加一个条件，这个条件可以是（只需填一个条件）．15.如图，在Rt△ABC中，∠C＝90°，AD是三角形的角平分线，如果AB＝3，AC＝2，那么点D到直线AB的距离等于．16.如图，斜坡AB长为100米，坡角∠ABC＝30°，现因“改小坡度”工程的需要，将斜坡AB改造成坡度i＝1：5的斜坡BD（A、D、C三点在地面的同一条垂线上），那么由点A到点D下降了﹣米．（结果保留根号）17.如图，在四边形ABCD中，∠ABC＝90°，对角线AC、BD交于点O，AO＝CO，CD⊥BD，如果CD＝3，BC＝5，那么AB＝．18.如图，在Rt△ABC中，∠C＝90°，AC＝5，sin B＝，点P为边BC上一点，PC＝3，将△ABC绕点P旋转得到△A'B'C'（点A、B、C分别与点A'、B'、C'对应），使B'C'∥AB，边A'C'与边AB交于点G，那么A'G的长等于．三、解答题（共7小题）19.计算：．20.如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，DE∥BC，EF∥AB，AD：AB＝1：3．（1）当DE＝5时，求FC的长；（2）设＝，＝，那么＝﹣，＝﹣（用向量，表示）．21.如图，在△ABC中，点P、D分别在边BC、AC上，P A⊥AB，垂足为点A，DP⊥BC，垂足为点P，＝．（1）求证：∠APD＝∠C；（2）如果AB＝3，DC＝2，求AP的长．22.函数y＝与函数y＝（m、k为不等于零的常数）的图象有一个公共点A（3，k﹣2），其中正比例函数y的值随x的值增大而减小，求这两个函数的解析式．23.已知：如图，四边形ABCD的对角线AC、BD相交于点O，S△AOD＝S△BOC．（1）求证：＝；（2）设△OAB的面积为S，＝k，求证：S四边形ABCD＝（k+1）2S．24.在平面直角坐标系xOy中（如图），已知抛物线y＝ax2+（a+）x+c（a≠0）经过点A（﹣3，﹣2），与y轴交于点B（0，﹣2），抛物线的顶点为点C，对称轴与x轴交于点D．（1）求抛物线的表达式及点C的坐标；（2）点E是x轴正半轴上的一点，如果∠AED＝∠BCD，求点E的坐标；（3）在（2）的条件下，点P是位于y轴左侧抛物线上的一点，如果△P AE是以AE为直角边的直角三角形，求点P的坐标．25.如图，在梯形ABCD中，AD∥BC，∠C＝90°，AD＝2，BC＝5，DC＝3，点E在边BC上，tan∠AEC＝3，点M是射线DC上一个动点（不与点D、C重合），联结BM交射线AE于点N，设DM＝x，AN ＝y．（1）求BE的长；（2）当动点M在线段DC上时，试求y与x之间的函数解析式，并写出函数的定义域；（3）当动点M运动时，直线BM与直线AE的夹角等于45°，请直接写出这时线段DM的长．2020年上海市普陀区中考数学一模试卷参考答案一、单选题（共6小题）1.【分析】根据比例的性质作答．【解答】解：A、由比例的性质得到3y＝5x，故本选项不符合题意．B、根据比例的性质得到x+y＝8k（k是正整数），故本选项符合题意．C、根据合比性质得到＝，故本选项不符合题意．D、根据等比性质得到＝，故本选项不符合题意．故选：B．【知识点】比例的性质2.【分析】由已知可知对称轴为x＝0，从而确定函数解析式y＝ax2+bx+c中，b＝0，由选项入手即可．【解答】解：二次函数的对称轴为y轴，则函数对称轴为x＝0，即函数解析式y＝ax2+bx+c中，b＝0，故选：C．【知识点】二次函数的性质3.【分析】利用同角三角函数的关系解答．【解答】解：在Rt△ABC中，∠C＝90°，sin A＝，则cos A＝＝＝A、cos B＝sin A＝，故本选项符合题意．B、cot A＝＝＝2．故本选项不符合题意．C、tan A＝＝＝．故本选项不符合题意．D、cot B＝tan A＝．故本选项不符合题意．故选：A．【知识点】同角三角函数的关系4.【分析】根据平面向量的性质一一判断即可．【解答】解：A、如果k＝0，是非零向量，那么k＝0，错误，应该是k＝．B、如果是单位向量，那么＝1，错误．应该是||＝1．C、如果||＝||，那么＝或＝﹣，错误．模相等的向量，不一定平行．D、已知非零向量，如果向量＝﹣5，那么∥，正确．故选：D．【知识点】*平面向量5.【分析】由二次函数解析式表示出顶点坐标，根据图形得到顶点在第四象限，求出m与n的正负，即可作出判断．【解答】解：根据题意得：抛物线的顶点坐标为（m，n），且在第四象限，∴m＞0，n＜0，则一次函数y＝mx+n经过第一、三、四象限．故选：B．【知识点】二次函数的性质、一次函数的性质、一次函数图象上点的坐标特征、二次函数图象上点的坐标特征、二次函数的图象6.【分析】证明△ADC∽△CDB，根据相似三角形的性质求出CD、BD，根据勾股定理求出BC．【解答】解：∵∠ACB＝90°，∴∠ACD+∠BCD＝90°，∵CD⊥AB，∴∠A+∠ACD＝90°，∴∠A＝∠BCD，又∠ADC＝∠CDB，∴△ADC∽△CDB，∴＝，＝，∴＝，即＝，解得，CD＝6，∴＝，解得，BD＝4，∴BC＝＝＝2，故选：C．【知识点】相似三角形的判定与性质二、填空题（共12小题）7.【分析】直接利用向量加减运算法则去括号合并求出答案．【解答】解：2（+）﹣（﹣）＝2+﹣+＝+2．故答案为：+2．【知识点】*平面向量8.【分析】利用二次函数的性质得到抛物线开口向下，则a﹣2＜0，然后解不等式即可．【解答】解：∵抛物线y＝（a﹣2）x2在对称轴左侧的部分是上升的，∴抛物线开口向下，∴a﹣2＜0，解得a＜2．故答案为a＜2．【知识点】二次函数图象上点的坐标特征、二次函数图象与系数的关系9.【分析】把x＝2代入函数关系式即可求得．【解答】解：f（2）＝3×22﹣2×2﹣1＝7，故答案为7．【知识点】二次函数的性质10.【分析】根据抛物线y＝ax2+2ax+c，可以得到该抛物线的对称轴，然后根据二次函数图象具有对称性和抛物线y＝ax2+2ax+c与x轴的一个交点的坐标是（1，0），可以得到该抛物线与x轴的另一个交点坐标．【解答】解：∵抛物线y＝ax2+2ax+c＝a（x+1）2﹣a+c，∴该抛物线的对称轴是直线x＝﹣1，∵抛物线y＝ax2+2ax+c与x轴的一个交点的坐标是（1，0），∴该抛物线与x轴的另一个交点的坐标是（﹣3，0），故答案为：（﹣3，0）．【知识点】抛物线与x轴的交点11.【分析】利用平移的性质得出平移后解析式，进而得出其顶点坐标，再代入直线y＝0求出即可．【解答】解：y＝x2﹣2x+2＝（x﹣1）2+1，∴将抛物线y＝x2﹣2x+2沿y轴向下平移1个单位，使平移后的抛物线的顶点恰好落在x轴上，∴m＝1，故答案为：1．【知识点】二次函数的性质、二次函数图象上点的坐标特征、二次函数图象与几何变换12.【分析】根据三角函数的定义即可求解．【解答】解：∵cot B＝，∴AC＝＝＝3BC＝6．故答案是：6．【知识点】锐角三角函数的定义13.【分析】根据三角形的重心和相似三角形的判定和性质解答即可．【解答】解：∵△ABC的中线AD、CE交于点G，∴G是△ABC的重心，∴，∵GF∥BC，∴＝，∵DC＝BC，∴，故答案为：【知识点】三角形的重心、相似三角形的判定与性质14.【分析】根据两边及其夹角法：两组对应边的比相等且夹角对应相等的两个三角形相似可得添加条件：∠B＝∠E．【解答】解：添加条件：∠B＝∠E；∵，∠B＝∠E，∴△ABC∽△AED，故答案为：∠B＝∠E（答案不唯一）．【知识点】相似三角形的判定15.【分析】作DE⊥AB于E，如图，利用勾股定理计算出BC＝5，再根据角平分线的性质得DC＝DE，然后利用面积法得到×2×DC+×DE×3＝×2×5，从而可求出DE．【解答】解：作DE⊥AB于E，如图，在Rt△ABC中，BC＝＝5，∵AD是三角形的角平分线，∴DC＝DE，∵S△ACD+S△ABD＝S△ABC，∴×2×DC+×DE×3＝×2×5，∴DE＝2，即点D到直线AB的距离等于2．故答案为2．【知识点】角平分线的性质16.【分析】根据直角三角形的性质求出AC，根据余弦的定义求出BC，根据坡度的概念求出CD，结合图形计算，得到答案．【解答】解：在Rt△ABC中，∠ABC＝30°，∴AC＝AB＝50，BC＝AB•cso∠ABC＝50，∵斜坡BD的坡度i＝1：5，∴DC：BC＝1：5，∴DC＝10，则AD＝50﹣10，故答案为：50﹣10．【知识点】解直角三角形的应用-坡度坡角问题17.【分析】如图，过点A作AE⊥BD，由“AAS”可证△AOE≌△COD，可得CD＝AE＝3，由勾股定理可求BD＝4，通过证明△ABE∽△BCD，可得，即可求解．【解答】解：如图，过点A作AE⊥BD，∵CD⊥BD，AE⊥BD，∴∠CDB＝∠AED＝90°，且CO＝AO，∠COD＝∠AOE，∴△AOE≌△COD（AAS）∴CD＝AE＝3，∵∠CDB＝90°，BC＝5，CD＝3，∴DB＝＝＝4；∵∠ABC＝∠AEB＝90°，∴∠ABE+∠EAB＝90°，∠CBD+∠ABE＝90°，∴∠EAB＝∠CBD，且∠CDB＝∠AED＝90°，∴△ABE∽△BCD，∴，∴∴AB＝故答案为：．【知识点】相似三角形的判定与性质18.【分析】如图，作PH⊥AB于H．利用相似三角形的性质求出PH，再证明四边形PHGC′是矩形即可解决问题．【解答】解：如图，作PH⊥AB于H．在Rt△ABC中，∠C＝90°，AC＝5，sin B＝，∴＝，∴AB＝13，BC＝＝＝12，∵PC＝3，∴PB＝9，∵∠BPH∽△BAC，∴＝，∴＝，∴PH＝，∵AB∥B′C′，∴∠HGC′＝∠C′＝∠PHG＝90°，∴四边形PHGC′是矩形，∴CG′＝PH＝，∴A′G＝5﹣＝，故答案为．【知识点】解直角三角形、平行线的判定、旋转的性质三、解答题（共7小题）19.【分析】根据特殊角三角函数值，可得实数的运算，根据实数的运算，可得答案．【解答】解：原式＝＝＝＝3+2．【知识点】特殊角的三角函数值20.【分析】（1）利用平行线分线段成比例定理求解即可．（2）利用三角形法则求解即可．【解答】解：（1）∵DE∥BC，EF∥AB，∴四边形DEFB是平行四边形，∴DE＝BF＝5，∵AD：AB＝DE：BC＝1：3，∴BC＝15，∴CF＝BC﹣BF＝15﹣5＝10．（2）∵AD：AB＝1：3，∴＝2＝2，∵EF＝BD，EF∥BD，∴＝﹣＝﹣2，∵CF＝2DE，∴＝＝，∴＝+＝﹣，故答案为【知识点】*平面向量21.【分析】（1）通过证明Rt△ABP∽Rt△PCD，可得∠B＝∠C，∠APB＝∠CDP，由外角性质可得结论；（2）通过证明△APC∽△ADP，可得，即可求解．【解答】证明：（1）∵P A⊥AB，DP⊥BC，∴∠BAP＝∠DPC＝90°，∵＝∴，∴Rt△ABP∽Rt△PCD，∴∠B＝∠C，∠APB＝∠CDP，∵∠DPB＝∠C+∠CDP＝∠APB+∠APD，∴∠APD＝∠C；（2）∵∠B＝∠C，∴AB＝AC＝3，且CD＝2，∴AD＝1，∵∠APD＝∠C，∠CAP＝∠P AD，∴△APC∽△ADP，∴∴AP2＝1×3＝3∴AP＝．【知识点】相似三角形的判定与性质22.【分析】把点A（3，k﹣2）代入y＝，即可得出，据此求出k的值，再根据正比例函数y的值随x的值增大而减小，得出满足条件的k值即可求解．【解答】解：根据题意可得，整理得k2﹣2k+3＝0，解得k1＝﹣1，k2＝3，∵正比例函数y的值随x的值增大而减小，∴k＝﹣1，∴点A的坐标为（3，﹣3），∴反比例函数是解析式为：；正比例函数的解析式为：y＝﹣x．【知识点】反比例函数与一次函数的交点问题23.【分析】（1）由S△AOD＝S△BOC易得S△ADB＝S△ACB，根据三角形面积公式得到点D和点C到AB的距离相等，则CD∥AB，于是可判断△DOC∽△BOA，然后利用相似比即可得到结论；（2）利用相似三角形的性质可得结论．【解答】证明：（1）∵S△AOD＝S△BOC，∴S△AOD+S△AOB＝S△BOC+S△AOB，即S△ADB＝S△ACB，∴CD∥AB，∴△DOC∽△BOA，∴；（2）∵△DOC∽△BOA∴，＝k2，∴DO＝kOB，CO＝kAO，S△COD＝k2S，∴S△AOD＝kS△OAB＝kS，S△COB＝kS△OAB＝kS，∴S四边形ABCD＝S+kS+kS+k2S＝（k+1）2S．【知识点】相似三角形的判定与性质24.【分析】（1）将点A、B代入抛物线y＝ax2+（a+）x+c，即可求出抛物线解析式，再化为顶点式即可；（2）如图1，连接AB，交对称轴于点N，则N（﹣，﹣2），利用相等角的正切值相等即可求出EH的长，OE的长，可写出点E的坐标；（3）分∠EAP＝90°和∠AEP＝90°两种情况讨论，通过相似的性质，用含t的代数式表示出点P的坐标，可分别求出点P的坐标．【解答】解：（1）将点A（﹣3，﹣2）、B（0，﹣2）代入抛物线y＝ax2+（a+）x+c，得，，解得，a＝，c＝﹣2，∴y＝x2+4x﹣2＝（x+）2﹣5，∴抛物线解析式为y＝x2+4x﹣2，顶点C的坐标为（﹣，﹣5）；（2）如图1，连接AB，交对称轴于点N，则N（﹣，﹣2），在Rt△BCN中，tan∠BCN＝＝＝，∴tan∠AED＝，过点A作AH⊥DE于H，则tan∠AED＝＝＝，∴EH＝4，∴OE＝1，∴E（1，0）；（3）①如图2，当∠EAP＝90°时，∵∠HEA+∠HAE＝90，∠HAE+∠MAP＝90°，∴∠HEA＝∠MAP，又∠AHE＝∠PMA＝90°，∴△AHE∽△PMA，则＝，设PM＝t，则AM＝2t，将P（t﹣3，﹣2﹣2t）代入y＝x2+4x﹣2，得，t1＝0（舍去），t2＝，∴P1（﹣，﹣5）；②如图3，当∠AEP＝90°时，∵∠EAG+∠AEG＝90°，∠AEG+∠PEN＝90°，∴∠AEG＝∠EPN，又∵∠N＝∠G，∴△AEG∽△PEN，则＝＝，设PN＝t，则EN＝2t，将P（1﹣t，2t）代入y＝x2+4x﹣2，得，t1＝，t2＝（舍），∴P2（﹣，）；综上所述：P1（﹣，﹣5），P2（﹣，）．【知识点】二次函数综合题25.【分析】（1）如图1中，作AH⊥BC于H，解直角三角形求出EH，CH即可解决问题．（2）延长AD交BM的延长线于G．利用平行线分线段成比例定理构建关系式即可解决问题．（3）分两种情形：①如图3﹣1中，当点M在线段DC上时，∠BNE＝∠ABC＝45°．②如图3﹣2中，当点M在线段DC的延长线上时，∠ANB＝∠ABE＝45°，利用相似三角形的性质即可解决问题．【解答】解：（1）如图1中，作AH⊥BC于H，∵AD∥BC，∠C＝90°，∴∠AHC＝∠C＝∠D＝90°，∴四边形AHCD是矩形，∴AD＝CH＝2，AH＝CD＝3，∵tan∠AEC＝3，∴＝3，∴EH＝1，CE＝1+2＝3，∴BE＝BC﹣CE＝5﹣3＝2．（2）延长AD交BM的延长线于G．∵AG∥BC，∴＝，∴＝，∴DG＝，AG＝2+＝，∵＝，∴＝，∴y＝（0＜x＜3）．（3）①如图3﹣1中，当点M在线段DC上时，∠BNE＝∠ABC＝45°，∵△EBN∽△EAB，∴EB2＝EN•AE，∴，解得x＝．②如图3﹣2中，当点M在线段DC的延长线上时，∠ANB＝∠ABE＝45°，∵△BNA∽△EBA，∴AB2＝AE•AN，∴（3）2＝•[+解得x＝13，综上所述DM的长为或13．【知识点】四边形综合题。

上海市普陀区中考数学一模试卷一、选择题：（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上]1.下列函数中，y关于x的二次函数是（） A．y=ax2+bx+c B．y=x（x﹣1）C．D．y=（x﹣1）2﹣x2【分析】根据二次函数的定义，逐一分析四个选项即可得出结论．【解答】解：A、当 a=0 时，y=bx+c 不是二次函数；B、y=x（x﹣1）=x2﹣x 是二次函数；C、y=不是二次函数；D、y=（x﹣1）2﹣x2=﹣2x+1 为一次函数．故选：B．【点评】本题考查了二次函数的定义，牢记二次函数的定义是解题的关键．2.在Rt△ABC中，∠C=90°，AC=2，下列结论中，正确的是（）A．AB=2sinA B．AB=2cosA C．BC=2tanA D．BC=2cotA【分析】直接利用锐角三角函数关系分别计算得出答案．【解答】解：∵∠C=90°，AC=2，∴cosA==，故AB=，故选项 A，B 错误；A ．tanA= = ，则 BC=2tanA ，故选项 C 正确；则选项 D 错误． 故选：C ．【点评】此题主要考查了锐角三角函数关系，正确将记忆锐角三角函数关系是解题关键．3. 如图，在△ABC中，点D 、E 分别在边AB 、AC 的反向延长线上，下面比例式中，不能判断ED∥BC的是（）B ．C ．D ．【分析】根据平行线分线段成比例定理，对各选项进行逐一判断即可． 【解答】解：A ．当时，能判断ED∥BC；B. 当时，能判断ED∥BC；C. 当时，不能判断ED∥BC；D. 当时，能判断ED∥BC；故选：C ．【点评】本题考查的是平行线分线段成比例定理，如果一条直线截三角形的两边 （或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边．4.已知，下列说法中，不正确的是（）A．B．与方向相同C．D．【分析】根据平行向量以及模的定义的知识求解即可求得答案，注意掌握排除法在选择题中的应用．【解答】解：A、错误．应该是﹣5=；B、正确．因为，所以与的方向相同；C、正确．因为，所以∥；D、正确．因为，所以||=5||；故选：A．【点评】本题考查了平面向量，注意，平面向量既有大小，又由方向，平行向量，也叫共线向量，是指方向相同或相反的非零向量．零向量和任何向量平行．5.如图，在平行四边形ABCD中，F是边AD上的一点，射线CF和BA的延长线交于点E，如果，那么的值是（）A．B．C．D．【分析】根据相似三角形的性质进行解答即可．【解答】解：∵在平行四边形 ABCD 中，∴AE∥CD，∴△EAF∽△CDF，∵，∴，∴，∵AF∥BC，∴△EAF∽△EBC，∴=，故选：D．【点评】此题考查相似三角形的判定和性质，综合运用了平行四边形的性质和相似三角形的性质是解题关键．6.如图，已知AB和CD是⊙O的两条等弦．OM ⊥AB，ON⊥CD，垂足分别为点M、N，BA、DC的延长线交于点P，联结OP．下列四个说法中：①；②OM=ON；③PA=PC；④∠BPO=∠DPO，正确的个数是（）A．1 B．2 C．3 D．4【分析】如图连接 OB、OD，只要证明Rt△OMB≌Rt△OND，Rt△OPM≌Rt△OPN 即可解决问题．【解答】解：如图连接 OB、OD；∵AB=CD，∴=，故①正确∵OM⊥AB，ON⊥CD，∴AM=MB，CN=ND，∴BM=DN，∵OB=OD，∴Rt△OMB≌Rt△OND，∴OM=ON，故②正确，∵OP=OP，∴Rt△OPM≌Rt△OPN，∴PM=PN，∠OPB=∠OPD，故④正确，∵AM=CN，∴PA=PC，故③正确，故选：D．【点评】本题考查垂径定理、圆心角、弧、弦的关系、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线面构造全等三角形解决问题，属于中考常考题型．二．填空题（本大题共 12 题，每题 4 分，满分 48 分）7．如果 =，那么= ．【分析】利用比例的性质由=得到=，则可设a=2t，b=3t，然后把a=2t，b=3t代入中进行分式的运算即可．【解答】解：∵=，∴=，设 a=2t，b=3t，∴==．故答案为．【点评】本题考查了比例的性质：常用的性质有：内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质．8．已知线段a=4厘米，b=9厘米，线段c是线段a和线段b的比例中项，线段c的长度等于6厘米．【分析】根据比例中项的定义，列出比例式即可得出中项，注意线段不能为负．【解答】解：根据比例中项的概念结合比例的基本性质，得：比例中项的平方等于两条线段的乘积．所以c2=4×9，解得c=±6（线段是正数，负值舍去），∴c=6cm，故答案为：6．【点评】本题考查比例线段、比例中项等知识，解题的关键是熟练掌握基本概念，属于中考常考题型．9．化简：=﹣4+7 ．【分析】根据屏幕绚丽的加法法则计算即可【解答】解：：=﹣4+6=﹣4+7，故答案为；【点评】本题考查平面向量的加减法则，解题的关键是熟练掌握平面向量的加减法则，注意平面向量的加减适合加法交换律以及结合律，适合去括号法则．10.在直角坐标系平面内，抛物线y=3x2+2x在对称轴的左侧部分是下降的（填“上升”或“下降”）【分析】由抛物线解析式可求得其开口方向，再结合二次函数的增减性则可求得答案．【解答】解：∵在 y=3x2+2x 中，a=3＞0，∴抛物线开口向上，∴在对称轴左侧部分 y 随 x 的增大而减小，即图象是下降的，故答案为：下降．【点评】本题主要考查二次函数的性质，利用二次函数的解析式求得抛物线的开口方向是解题的关键．11.二次函数y=（x﹣1）2﹣3的图象与y轴的交点坐标是（0，﹣2）．【分析】求自变量为0时的函数值即可得到二次函数的图象与y轴的交点坐标．【解答】解：把x=0代入y=（x﹣1）2﹣3得y=1﹣3=﹣2，所以该二次函数的图象与y轴的交点坐标为（0，﹣2），故答案为（0，﹣2）．【点评】本题考查了二次函数图象上点的坐标特征，在y轴上的点的横坐标为0．12.将抛物线y=2x2平移，使顶点移动到点P（﹣3，1）的位置，那么平移后所得新抛物线的表达式是y=2（x+3）2+1 ．【分析】由于抛物线平移前后二次项系数不变，然后根据顶点式写出新抛物线解析式．【解答】解：抛物线 y=2x2 平移，使顶点移到点 P（﹣3，1）的位置，所得新抛物线的表达式为 y=2（x+3）2+1．故答案为：y=2（x+3）2+1．【点评】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．13.在直角坐标平面内有一点A（3，4），点A与原点O的连线与x轴的正半轴夹角为α，那么角α的余弦值是．【分析】利用锐角三角函数的定义、坐标与图形性质以及勾股定理的知识求解．【解答】解：∵在直角坐标平面内有一点A（3，4），∴OA==5，∴cosα= ．故答案为：．【点评】本题考查了解直角三角形、锐角三角函数的定义、坐标与图形性质以及勾股定理的知识，此题比较简单，易于掌握．14.如图，在△ABC中，AB=AC，点D、E分别在边BC、AB上，且∠ADE=∠B，如果DE：AD=2：5，BD=3，那么AC= ，．【分析】根据∠ADE=∠B，∠EAD=∠DAB，得出△AED∽△ABD，利用相似三角形的性质解答即可．【解答】解：∵∠ADE=∠B，∵∠EAD=∠DAB，∴△AED∽△ABD，∴，即，∴AB=，∵AB=AC，∴AC=，故答案为：，【点评】本题考查了相似三角形的判定与性质．关键是要懂得找相似三角形，利用相似三角形的性质求解．15.如图，某水库大坝的横断面是梯形ABCD，坝顶宽AD=6米，坝高是20 米，背水坡 AB的坡角为30°，迎水坡CD的坡度为1：2，那么坝底 BC 的长度等于（46+20）米（结果保留根号）【分析】过梯形上底的两个顶点向下底引垂线AE、DF，得到两个直角三角形和一个矩形，分别解Rt△ABE、Rt△DCF求得线段BE、CF的长，然后与EF 相加即可求得 BC 的长．【解答】解：如图，作AE⊥BC，DF⊥BC，垂足分别为点E，F，则四边形ADFE 是矩形．由题意得，EF=AD=6 米，AE=DF=20 米，∠B=30°，斜坡 CD 的坡度为 1： 2，在Rt△ABE 中，∵∠B=30°，∴BE=AE=20米．在Rt△CFD中，∵=，∴CF=2DF=40 米，∴BC=BE+EF+FC=20+6+40=46+20（米）．所以坝底BC的长度等于（46+20）米．故答案为（46+20）．【点评】此题考查了解直角三角形的应用﹣坡度坡角问题，难度适中，解答本题的关键是构造直角三角形和矩形，注意理解坡度与坡角的定义．16.已知Rt△ABC中，∠C=90°，AC=3，BC=，CD⊥AB，垂足为点D，以点D为圆心作⊙D，使得点A在⊙D外，且点B在⊙D内．设⊙D的半径为r，那么r的取值范围是．【分析】先根据勾股定理求出AB的长，进而得出CD的长，由点与圆的位置关系即可得出结论．【解答】解：∵Rt△ABC中，∠ACB=90，AC=3，BC=，∴AB==4．∵CD⊥AB，∴CD=．∵AD•BD=CD2，设AD=x，BD=4﹣x．解得x=∴点 A 在圆外，点 B 在圆内，r的范围是，故答案为：．【点评】本题考查的是点与圆的位置关系，熟知点与圆的三种位置关系是解答此题的关键．17.如图，点D在△ABC的边BC上，已知点E、点F分别为△ABD和△ADC 的重心，如果BC=12，那么两个三角形重心之间的距离EF的长等于4 ．【分析】连接AE并延长交BD于 G，连接AF并延长交CD于 H，根据三角形的重心的概念、相似三角形的性质解答．【解答】解：如图，连接 AE 并延长交 BD 于 G，连接 AF 并延长交 CD 于 H，∵点 E、F 分别是△ABD 和△ACD 的重心，∴DG=BD，DH=CD，AE=2GE，AF=2HF，∵BC=12，∴GH=DG+DH= （BD+CD）= BC= ×12=6，∵AE=2GE，AF=2HF，∠EAF=∠GAH，∴△EAF∽△GAH，∴==，∴EF=4，故答案为：4．【点评】本题考查了三角形重心的概念和性质，三角形的重心是三角形中线的交点，三角形的重心到顶点的距离等于到对边中点的距离的2倍．18.如图，△ABC中，AB=5，AC=6，将△ABC翻折，使得点A落到边BC 上的点A′处，折痕分别交边AB、AC于点E，点F，如果A′F∥AB，那么BE= ．【分析】设BE=x，则AE=5﹣x=AF=A'F，CF=6﹣（5﹣x）=1+x，依据△A'CF ∽△BCA，可得=，即=，进而得到BE=．【解答】解：如图，由折叠可得，∠AFE=∠A'FE，∵A'F∥AB，∴∠AEF=∠A'FE，∴∠AEF=∠AFE，∴AE=AF，由折叠可得，AF=A'F，设 BE=x，则 AE=5﹣x=AF=A'F，CF=6﹣（5﹣x）=1+x，∵A'F∥AB，∴△A'CF∽△BCA，∴=，即=，解得x=，∴BE=，故答案为：．【点评】本题主要考查了折叠问题以及相似三角形的判定与性质的运用，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，对应边和对应角相等．三、解答题（本大题共 7 题，满分 78 分）19．（10分）计算：45°．【分析】直接利用特殊角的三角函数值进而代入化简得出答案．【解答】解：原式=﹣×= ﹣= ．【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键． 20．（10分）已知一个二次函数的图象经过A（0，﹣3），B（1，0），C（m，2m+3），D（﹣1，﹣2）四点，求这个函数解析式以及点C的坐标．【分析】设一般式y=ax2+bx+c，把A、B、D点的坐标代入得，然后解法组即可得到抛物线的解析式，再把 C（m，2m+3）代入解析式得到关于 m 的方程，解关于 m 的方程可确定 C 点坐标．【解答】解：设抛物线的解析式为 y=ax2+bx+c，把A（0，﹣3），B（1，0），D（﹣1，﹣2）代入得，解得，∴抛物线的解析式为 y=2x2+x﹣3，把C（m，2m+3）代入得2m2+m﹣3=2m+3，解得m1=﹣，m2=2，∴C点坐标为（﹣，0）或（2，7）．【点评】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与 x 轴有两个交点时，可选择设其解析式为交点式来求解．21．（10分）如图，已知⊙O经过△ABC的顶点A、B，交边BC于点D，点A恰为的中点，且BD=8，AC=9，sinC=，求⊙O的半径．【分析】如图，连接OA．交BC于H．首先证明OA⊥BC，在Rt△ACH中，求出AH，设⊙O的半径为r，在Rt△BOH中，根据BH2+OH2=OB2，构建方程即可解决问题；【解答】解：如图，连接 OA．交 BC 于 H．∵点A为的中点，∴OA⊥BD，BH=DH=4，∴∠AHC=∠BHO=90°，∵sinC==，AC=9，∴AH=3，设⊙O 的半径为 r，在Rt△BOH 中，∵BH2+OH2=OB2，∴42+（r﹣3）2=r2，∴r=，∴⊙O的半径为．【点评】本题考查圆心角、弧、弦的关系、垂径定理、勾股定理、锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．22．（10分）下面是一位同学的一道作图题：已知线段a、b、c（如图），求作线段x，使a：b=c：x他的作法如下：（1）、以点O为端点画射线OM，ON．（2）、在OM上依次截取OA=a，AB=b．（3）、在ON上截取OC=c．（4）、联结AC，过点B作BD∥AC，交ON于点D．所以：线段CD就是所求的线段x．①试将结论补完整②这位同学作图的依据是平行于三角形一边的直线截其它两边（或两边的延长线），所得对应线段成比例③如果OA=4，AB=5，，试用向量表示向量．【分析】①根据作图依据平行线分线段成比例定理求解可得；②根据“平行于三角形一边的直线截其它两边（或两边的延长线），所得对应线段成比例”可得；③先证△OAC∽△OBD得= ，即BD= AC，从而知= =﹣=﹣．【解答】解：①根据作图知，线段 CD 就是所求的线段 x，故答案为：CD；②这位同学作图的依据是：平行于三角形一边的直线截其它两边（或两边的延长线），所得对应线段成比例；故答案为：平行于三角形一边的直线截其它两边（或两边的延长线），所得对应线段成比例；③∵OA=4、AB=5，且BD∥AC，∴△OAC∽△OBD，∴=，即=，∴BD=AC，∴= =﹣=﹣．【点评】本题主要考查作图﹣复杂作图，解题的关键是熟练掌握平行线分线段成比例定理及向量的计算．23．（12分）已知：如图，四边形ABCD的对角线AC和BD相交于点E，AD=DC，DC2=DE•DB，求证：（1）△BCE∽△ADE；（2）AB•BC=BD•BE．【分析】（1）由∠DAC=∠DCA，对顶角∠AED=∠BEC，可证△BCE∽△ADE．（2）根据相似三角形判定得出△ADE∽△BDA，进而得出△BCE∽△BDA，利用相似三角形的性质解答即可．【解答】证明：（1）∵AD=DC，∴∠DAC=∠DCA，∵DC2=DE•DB，∴=，∵∠CDE=∠BDC，∴△CDE∽△BDC，∴∠DCE=∠DBC，∴∠DAE=∠EBC，∵∠AED=∠BEC，∴△BCE∽△ADE，（2）∵DC2=DE•DB，AD=DC∴AD2=DE•DB，同法可得△ADE∽△BDA，∴∠DAE=∠ABD=∠EBC，∵△BCE∽△ADE，∴∠ADE=∠BCE，∴△BCE∽△BDA，∴= ，∴AB•BC=BD•BE．【点评】本题考查了相似三角形的判定与性质．关键是要懂得找相似三角形，利用相似三角形的性质求解．24．（12分）如图，已知在平面直角坐标系中，已知抛物线y=ax2+2ax+c（其中a、c为常数，且a＜0）与x轴交于点A，它的坐标是（﹣3，0），与y轴交于点B，此抛物线顶点C到x轴的距离为4（1）求抛物线的表达式；（2）求∠CAB的正切值；（3）如果点P是抛物线上的一点，且∠ABP=∠CAO，试直接写出点P的坐标．【分析】（1）先求得抛物线的对称轴方程，然后再求得点 C 的坐标，设抛物线的解析式为y=a（x+1）2+4，将点（﹣3，0）代入求得a的值即可；（2）先求得A、B、C的坐标，然后依据两点间的距离公式可得到BC、AB、AC的长，然后依据勾股定理的逆定理可证明∠ABC=90°，最后，依据锐角三角函数的定义求解即可；（3）记抛物线与x轴的另一个交点为D．先求得D（1，0），然后再证明∠DBO=∠CAB，从而可证明∠CAO=ABD，故此当点P与点D重合时，∠ABP=∠CAO；当点P在AB的上时．过点P作PE∥AO，过点B作BF∥AO，则PE∥BF．先证明∠EPB=∠CAB，则tan∠EPB=，设BE=t，则PE=3t，P（﹣3t，3+t），将P（﹣3t，3+t）代入抛物线的解析式可求得t的值，从而可得到点P 的坐标．【解答】解：（1）抛物线的对称轴为x=﹣=﹣1．∵a＜0，∴抛物线开口向下．又∵抛物线与 x 轴有交点，∴C 在 x 轴的上方，∴抛物线的顶点坐标为（﹣1，4）．设抛物线的解析式为 y=a（x+1）2+4，将点（﹣3，0）代入得：4a+4=0，解得：a=﹣1，∴抛物线的解析式为 y=﹣x2﹣2x+3．（2）将x=0代入抛物线的解析式得：y=3，∴B（0，3）．∵C（﹣1，4）、B（0，3）、A（﹣3，0），∴BC=，AB=3，AC=2，∴BC2+AB2=AC2，∴∠ABC=90°．∴tan∠CAB==．（3）如图1所示：记抛物线与x轴的另一个交点为D．∵点 D 与点 A 关于 x=﹣1 对称，∴D（1，0）．∴tan∠DBO=．又∵由（2）可知：tan∠CAB=．∴∠DBO=∠CAB．又∵OB=OA=3，∴∠BAO=∠ABO．∴∠CAO=∠ABD．∴当点 P 与点 D 重合时，∠ABP=∠CAO，∴P（1，0）．如图2所示：当点P在AB的上时．过点P作PE∥AO，过点B作BF∥AO，则PE∥BF．∵BF∥AO，∴∠BAO=∠FBA．又∵∠CAO=∠ABP，∴∠PBF=∠ CAB．又∵PE∥BF，∴∠EPB=∠PBF，∴∠EPB=∠CAB．∴tan∠EPB=．设BE=t，则PE=3t，P（﹣3t，3+t）．将P（﹣3t，3+t）代入抛物线的解析式得：y=﹣x2﹣2x+3得：﹣9t2+6t+3=3+t，解得t=0（舍去）或t=．∴P（﹣，）．综上所述，点P的坐标为P（1，0）或P（﹣，）．【点评】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、勾股定理的逆定理、等腰直角三角形的性质、锐角三角函数的定义，用含 t 的式子表示点 P 的坐标是解题的关键．25．（14分）如图1，∠BAC的余切值为2，AB=2，点D是线段AB上的一动点（点D不与点A、B重合），以点D为顶点的正方形DEFG的另两个顶点E、F都在射线AC上，且点F在点E的右侧，联结BG，并延长BG，交射线EC于点P．（1）点D在运动时，下列的线段和角中，④⑤是始终保持不变的量（填序号）；①AF；②FP；③BP；④∠BDG；⑤∠GAC；⑥∠BPA；（2）设正方形的边长为x，线段AP的长为y，求y与x之间的函数关系式，并写出定义域；（3）如果△PFG与△AFG相似，但面积不相等，求此时正方形的边长．【分析】（1）作BM⊥AC于M，交DG于N，如图，利用三角函数的定义得到=2，设BM=t，则AM=2t，利用勾股定理得（2t）2+t2=（2）2，解得t=2，即BM=2，AM=4，设正方形的边长为x，则AE=2x，AF=3x，由于tan∠GAF==，则可判断∠GAF为定值；再利用DG∥AP得到∠BDG=∠BAC，则可判断∠BDG为定值；在Rt△BMP中，利用勾股定理和三角函数可判断PB在变化，∠BPM在变化，PF在变化；（2）易得四边形DEMN为矩形，则NM=DE=x，证明△BDG∽△BAP，利用相似比可得到y与x的关系式；（3）由于∠AFG=∠PFG=90°，△PFG与△AFG相似，且面积不相等，利用相似比得到PF=x，讨论：当点P在点F点右侧时，则AP=x，所以=x，当点P在点F点左侧时，则AP= x，所以=x，然后分别解方程即可得到正方形的边长．【解答】解：（1）作BM⊥AC于M，交DG于N，如图，在Rt△ABM中，∵cot∠BAC==2，设 BM=t，则 AM=2t，∵AM2+BM2=AB2，∴（2t）2+t2=（2）2，解得t=2，∴BM=2，AM=4，设正方形的边长为 x，在Rt△ADE中，∵cot∠DAE==2，∴AE=2x，∴AF=3x，在Rt△GAF中，tan∠GAF===，∴∠GAF 为定值；∵DG∥AP，∴∠BDG=∠BAC，∴∠BDG 为定值；在Rt△BMP中，PB=，而PM在变化，∴PB 在变化，∠BPM 在变化，∴PF 在变化，所以∠BDG 和∠GAC 是始终保持不变的量；故答案为④⑤；（2）易得四边形DEMN为矩形，则NM=DE=x，∵DG∥AP，∴△BDG∽△BAP，∴=，即=，∴y=（1≤x＜2）（3）∵∠AFG=∠PFG=90°，△PFG与△AFG相似，且面积不相等，∴=，即=，∴PF=x，当点P在点F点右侧时，AP=x，∴=x，解得x=，当点P在点F点左侧时，AP=AF﹣PF=3x﹣x=x，∴=x，解得x=，综上所述，正方形的边长为或．【点评】本题考查了相似形综合题：熟练掌握锐角三角函数的定义、正方形的性质和相似三角形的判定与性质．。