吉林省吉林市朝鲜族中学高中数学 第二章 统计复习学案(无答案)新人教A版必修3

2.4等比数列【学习目标】理解等比数列、等比中项的概念，能推导并掌握通项公式，能熟练运用通项公式和一些常用性质解决有关问题． 【重点难点】重点：等比数列的定义和通项公式及其应用．难点：等比数列的通项公式的应用．【学法指导】学习本节一定要认真阅读教材，运用从特殊到一般和类比等差数列的定义、通项公式的方法归纳等比数列的定义、通项公式． 一.课前预习阅读课本4852P P 页，弄清下列问题：1．等比数列的概念： ．2．用数学式子表示等比数列的定义： {}n a 是等比数列，则*1()n na q n N a +=∈． 强调：（1）“从第二项起，每一项与它的前一项的比都等于同一个常数”，要防止在求公比 时，把相邻两项比的次序颠倒．（3）当公比q ＝ 时，等比数列是常数列，该数列也是等差数列．（4）等比数列的每一项都不为 ．3．等比数列的通项公式： ． 4．等比中项的定义： ． 5．快乐体验：(1)若等比数列155,45a a ==，求公比q ； (2)若等比数列12,33a q ==，求4a ．(3)若等比数列3312,2a q ==，求1a ； (4)若等比数列的12,54,3,n a a q ===求n ．(5)若4,9a b ==，求,a b 的等比中项．二．课堂学习与研讨例1．某种放射性物质不断变化为其他物质，每经过一年剩留量是原来的84%．这种物质的半衰期为多长？（精确到1年）（参考数据：lg 20.3010,lg0.840.0757,0.30100.0757 3.98==-÷≈）练习1．（教材53P 练习5）某人买了一辆价值13．5万元的新车，专家预测这种车每年按10%的速度折旧． （1）用一个式子表示*()n n N ∈年后这辆车的价值；（2）如果他打算用满4年时卖掉这辆车，他大概能得到多少钱？例2．等比数列的第3项和第4项分别是12和18，求它的第1项和第2项．练习2. 在等比数列{}n a 中，473,81,n a a a ==求.小结：3．等比中项：若,,a G b 成等比数列，则2G ab =． 三.课堂检测1．若a ,22a +,33a +成等比数列，则实数a 的为 ．2．在等比数列中，（1）若已知2514,2a a ==-求n a ． （2）若253618,9,1n a a a a a +=+==，求n .四．作业 1． P53A1 2. 在83和272之间插入3个数，使这五个数成等比数列，求这三数？3. 在等比数列{}n a 中，已知1910185,100,a a a a =⋅=求.2.5等比数列的前n 项和公式【学习目标】1.掌握等比数列的前n 项和公式11,1(1),11n n na q S a q q q =⎧⎪=-⎨⎪≠-⎩2.在等比数列{}n a 中，n n s n d a a 、、、、1五个量中“知三求二”.3.通过公式的灵活运用，进一步渗透方程的思想、分类讨论的思想和等价转化的思想. 【重点难点】重点：等比数列前n 项和公式的推导和运用.难点：等比数列前n 项和公式的推导. 【学法指导】学习本节时好好体会错位相减法求和的思路，分析等比数列的通项公式和前n 项和公式的特点，体会知三求二的方程思想． 一.课前预习 预习课本5557P P 页，回答下列问题：1．传说，很早以前，印度的一位宰相发明了国际象棋，当时的国王非常高兴，决定奖赏他，国王允许宰相提出任何要求，于是这位聪明的宰相便请国王在国际象棋棋盘的第一个格子里放入一颗麦粒，第二个格子里放入两颗麦粒，第三个……，就这样，依此类推，要求从第二个格子起，每个格子里的麦粒数是前一个格子里麦粒数的两倍，他请求国王给予他这些麦粒的总和。

吉林省吉林市朝鲜族中学2020高中数学 2.2.1 用样本的频率分布估计总体分布（第1课时）学案（无答案）新人教A版必修3学习目标（1）通过实例体会分布的意义和作用。

（2）在表示样本数据的过程中，学会列频率分布表，画频率分布直方图。

学习重点会列频率分布表，画频率分布直方图学习难点能通过样本的频率分布估计总体的分布学习内容学法指导一．知识点1. 频率分布的概念：频率分布：频率分布是指一个样本数据在各个小范围内所占的大小。

一般用频率分布直方图反映样本的频率分布。

频数及频率：将一批数据按要求分为若干个组，叫做该组的频数，每组的叫做该组的频率。

2.频率分布直方图（1）绘制步骤：①求，即一组数据中的最大值与最小值的差。

②决定与。

③将数据。

④列出表。

⑤画出频率分布直方图。

其中横轴表示，纵轴表示的比。

（2）意义：频率分布直方图中，每个小矩形的面积表示相应组的，所有小矩形的面积的总和等于。

二．典型例题例1：某地区为了了解知识分子的年龄结构，随机抽样50名，其年龄分别如下：42，38，29，36，41，43，54，43，34，44，40，59，39，42，44，50，37，44，45，29，48，45，53，48，37，28，46，50，37，44，42，39，51，52，62，47，59，46，45，67，53，49，65，47，54，63，57，43，46，58.(1)列出样本频率分布表；(2)画出频率分布直方图；(3)估计年龄在33～53岁的知识分子所占的比例约是多少. 注意掌握本题中关键是列出频率分别表三．当堂检测1.为了解一批数据在各个范围内所占的比例大小，将这批数据分组，落在各个小组里的数据个数叫做（）A、频数B、样本容量C、频率D、频数累计2.在频率分布直方图中，各个小长方形的面积表示（）A、落在相应各组的数据的频数B、相应各组的频率C、该样本所分成的组数D、该样本的容量3.为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17岁~18岁的男生体重(kg)，得到频率分布直方图，如图，据图可得这100名学生中体重在［56.5, 64.5) kg的学生人数是( )A .20 B．30 C．40 D．50 要牢固掌握列频率分别表及画频率分布直方图的步骤与方法检测练习：有一个容量为50的样本数据的分组的频数如下：［12.5, 15.5） 3 ［15.5, 18.5）8［18.5, 21.5）9［21.5, 24.5）11 ［24.5, 27.5）10 ［27.5, 30.5） 5［30.5, 33.5） 4(1)列出样本的频率分布表; (2)画出频率分布直方图;(3)根据频率分布直方图估计,数据落在[15.5, 24.5）的百分比是多少?。

2.2.1 用样本的频率分布估计总体分布A级基础巩固一、选择题1．没有信息的损失，所有的原始数据都可以从图中得到的统计图是( )A．总体密度曲线B．茎叶图C．频率分布折线图D．频率分布直方图答案：B2．下图是某公司10个销售店某月销售某产品数量(单位：台)的茎叶图，则数据落在区间[22，30)内的频率为( )B．C．D．解析：数据总个数n＝10，又落在区间[22，30)内的数据个数为4，故所求的频率为410＝0.4.答案：B3．某雷达测速区规定：凡车速大于或等于70 km/h的汽车视为“超速”，并将受到处罚．下图是某路段的一个检测点对300辆汽车的车速进行检测所得结果的频率分布直方图，则从图中可得出将被处罚的汽车数为( )A．30辆B．40辆C．60辆D．80辆解析：车速大于或等于70 km/h的汽车数为×10×300＝60(辆)．答案：C4．一个社会调查机构就某地区居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图(如图)，为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，则在[2 500，3 000)(单位：元)月收入段应抽出的人数为( )A．5 B．25 C．50 D．2 500解析：组距＝500，在[2 500，3 000)的频率＝0.000 5×500＝，样本数为100，则在[2 500，3 000)内应抽100×＝25(人)．答案：B5．为了了解某校高三学生的视力情况，随机抽查了该校100名高三学生的视力情况，得到频率分布直方图如图所示，由于不慎将部分数据丢失，仅知道后5组的频数和为62.设视力在到之间的学生数为a，最大频率为，则a的值为( )A．27 B．48 C．54 D．64解析：由已知，视力在到之间的学生数为100×＝32，又视力在到之间的频率为1－＋0.5)×－62100＝，所以视力在到之间的学生数为100×＝22，所以视力在到之间的学生数a ＝32＋22＝54.答案：C二、填空题6．某市共有5 000名高三学生参加联考，为了了解这些学生对数学知识的掌握情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：分组/分频数频率[80，90)①②[90，100)[100，110)[110，120)36[120，130)[130，140)12③[140，150]合计④根据上面的频率分布表，可以①处的数值为________，②处的数值为________． 解析：由位于[110，120)的频数为36，频率＝36n＝，得样本容量n ＝120，所以[130，140)的频率＝12120＝，②处的数值＝1－－－－－－＝； ①处的数值为×120＝3. 答案：37．从某小学随机抽取100名同学，将他们的身高(单位：cm)数据绘制成频率分布直方图(如图)．由图中数据可知a ＝________．若要从身高在[120，130)，[130，140)，[140，150]三组内的学生中，用分层抽样的方法抽取18人参加一项活动，则从身高在[140，150]内的学生中抽取的人数应为________．解析：所有小矩形的面积和等于10×＋＋0.020＋a ＋0.035)＝1，解得a ＝；100名同学中，身高在[120，130)内的学生数是10××100＝30，身高在[130，140)内的学生数是10××100＝20，身高在[140，150]内的学生数是10××100＝10，则三组内的总学生数是30＋20＋10＝60，抽样比是1860＝310，所以身高在[140，150]内的学生中选取的人数应为10×310＝3.答案： 38．为了解某校教师使用多媒体进行教学的情况，采用简单随机抽样的方法，从该校200名授课教师中抽取20名教师，调查了他们上学期使用多媒体进行教学的次数，结果用茎叶图表示如下：据此可估计该校上学期200名教师中，使用多媒体进行教学次数在[15，25)内的人数为________．答案：60三、解答题9．为了调查甲、乙两个网站受欢迎的程度，随机选取了14天，统计上午8：00－10：00间各自的点击量，得到如图所示的茎叶图．(1)甲网站点击量在[10，40]间的频率是多少？ (2)甲、乙两个网站哪个更受欢迎？请说明理由．解：(1)甲网站点击量在[10，40]内的有17，20，38，32，共有4天，则频率为414＝27. (2)甲网站的点击量集中在茎叶图的下方，而乙网站的点击量集中在茎叶图的上方，从数据的分布情况来看，甲网站更受欢迎．10．为了了解高一学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图)，图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3，第二小组频数为12.(1)第二小组的频率是多少？样本容量是多少？(2)若次数在110以上(含110次)为达标，试估计该学校全体高一学生的达标率是多少？ 解：(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小，因此第二小组的频率为：42＋4＋17＋15＋9＋3＝0.08.又因为第二小组的频率＝第二小组的频数样本容量，所以样本容量＝第二小组的频数第二小组的频率＝120.08＝150.(2)由题意估计该学校高一学生的达标率约为17＋15＋9＋32＋4＋17＋15＋9＋3×100%＝88%.B 级 能力提升1．为了研究某药品的疗效，选取若干名志愿者进行临床试验，所有志愿者的舒张压数据(单位：kPa)的分组区间为[12，13)，[13，14)，[14，15)，[15，16)，[16，17]，将其按从左到右的顺序分别编号为第一组，第二组，…，第五组，如图所示是根据试验数据制成的频率分布直方图．已知第一组与第二组共有20人，第三组中没有疗效的有6人，则第三组中有疗效的人数为( )A ．6B ．8C ．12D ．18解析：志愿者的总人数为20（＋）×1＝50，所以第三组的人数为50×＝18，有疗效的人数为18－6＝12.答案：C2．在一次马拉松比赛中，35名运动员的成绩(单位：分钟)的茎叶图如图所示．若将运动员按成绩由好到差编为1～35号，再用系统抽样方法从中抽取7人，则其中成绩在区间[139，151]上的运动员人数是________．解析：由题意可知，这35名运动员的分组情况为，第一组(130，130，133，134，135)，第二组(136，136，138，138，138)，第三组(139，141，141，141，142)，第四组(142，142，143，143，144)，第五组(144，145，145，145，146)，第六组(146，147，148，150，151)，第七组(152，152，153，153，153)，故成绩在区间[139，151]上的运动员恰有4组，则运动员人数为4.答案：43．从高一学生中抽取50名参加调研考试，成绩的分组及各组的频数如下(单位：分): [40，50)，2；[50，60)，3；[60，70)，10；[70，80)，15；[80，90)，12；[90，100]，8.(1)列出样本的频率分布表；(2)画出频率分布直方图；(3)估计成绩在[70，80)分的学生所占总体的百分比．解：(1)频率分布表如下：成绩分组频数频率[40，50)2[50，60)3[60，70)10[70，80)15[80，90)12[90，100]8合计50(2)由题意知组距为10，取小矩形的高根据表格画出如下的频率分布直方图：(3)由频率分布直方图，可估计成绩在[70，80)分的学生所占总体的百分比是×10＝＝30%.。

第二章统计教学目标重点：会用随机抽样的基本方法和样本估计总体的思想，解决一些简单的问题．难点：能通过对数据的分析，为合理的决策提供一些依据，认识统计的作用，体会统计思维与确定性思维的差异.能力点：如何利用样本对总体的分布规律、整体水平、稳定程度及相关关系等特性进行估计和预测．教育点：提高学生的认知水平，为学生塑造良好的数学认识结构.自主探究点：例题及变式的解题思路的探寻.易错点：由于学生运算能力差，因此求回归直线方程涉及的运算学生容易出错.学法与教具1.学法：讲授法、讨论法.2.教具：学案导学.(1)作样本频率分布直方图的步骤：注意：频率分布直方图纵坐标表示：____________．(2)茎叶图作图步骤:(3)直方图与茎叶图的优缺点：3.用样本的数据特征估计总体的数据特征(1)利用频率直方图中估计众数、平均数、中位数的值：估计众数______________________________________．估计平均数____________________________________．估计中位数____________________________________．(2)标准差与方差的公式：标准差____________________s=．方差2_____________________s=．(3)标准差与方差的作用：4.变量间的相关关系(1)两变量间的关系有：________________和________________．(2)两变量相关关系的确定方法：____________________________________．(3)用最小二乘法求回归直线方程的步骤：（二）基础检测1.某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，为了调查社会购买力的某项指标，要从中抽取1个容量为100户的样本，记做①；某学校高一年级有12名女排运动员，要从中选出3个调查学习负担情况，记做②.那么完成上述2项调查应采用的抽样方法分别是________________．答案：分层抽样，简单随机抽样．2.一个总体的60个个体的编号为0，1，2，…，59，现要从中抽取一个容量为10的样本，请根据编号按被6样本，则抽取的样本号码是_______________．答案：3，9，15，21，27，33，39，45，51，3.(12山东文高考) 右图是根据部分城市某年6气温(单位:℃)数据得到的样本频率分布直方图气温的范围是[20.5,26.5],样本数据的分组为[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为_________．答案：9．/第3题图4.(10山东理)样本中共有五个个体，其值分别为a ,0,1,2,3， 若该样本的平均值为1，则样本方差为_______________． 答案：2．5.(11辽宁)调查了某地若干户家庭的年收入x （单位：万元）和年饮食支出y （单位：万元），调查显示年收入x 和年饮食支出y 具有线性相关关系，并由调查数据得到y 对x 的回归直线方程：0.2540.321y x =+．由回归直线方程可知，家庭年收入每增加1万元，年饮食支出平均增加_______________万元．答案：0.254． 三、【范例导航】例1．一汽车厂生产A ，B ，C 三类轿车，每类轿车均有舒适型和标A 类轿车10辆．(1)求z 的值； (2)B 类，C 类轿车各应抽取多少？ (3)在C 类轿车中，按型号分层抽样，应各抽取多少？【分析】按类分层或者是按型号分层，抽样比是相同的．【解答】(1)设该厂这个月共生产轿车n 辆，则由题意得5010,100300n =+所以2000n =， 则2000(100300)150450600400z =-+---=.(2)B 类轿车共有150＋450＝600(辆)．按抽样比10400抽取，则应抽取1060015400⨯=(辆)． 同理，C 类应抽取10(400600)25400+⨯=(辆)．(3)在C 类轿车中，按型号抽样时抽样比仍为140.则舒适型应抽取14001040⨯=(辆)；标准型应抽取16001540⨯=(辆)．【点评】通过本题的具体计算可看出，无论是按类抽取还是按型号抽取，每个个体入样的概率都是140. 变式训练：为了了解参加某种知识竞赛的1000名学生的成绩，要从中抽取50名学生的成绩，采用什么抽样方法比较恰当？简述抽样过程． 答案：适宜选用系统抽样，抽样过程如下：(1)随机地将这1000名学生编号为1,2,3,,1000；(2)将总体按编号顺序均分成50部分，每部分包括20个个体； (3)在第一部分的个体编号1,2,3,,20中，利用简单随机抽样抽取一个号码，比如是18；(4) 以18为起始号码，每间隔20抽取一个号码，这样得到一个容量为50的样本：18,38,58,, 998． 小结：1.三种抽样方法的共同特点是在抽样过程中每个个体被抽取的机会相同，体现了这些抽样方法的客观性和公平性．2.当总体中的个体数较少时，常采用简单随机抽样；当总体中的个体数较多时，常采用系统抽样；当总体中的个体有明显的层次差异，层次分明时，常采用分层抽样．3.系统抽样时要注意所得样本号码的特点，而分层抽样要正确确定抽样的比例．例2．为了了解高二学生的体能情况，我校抽取部分高二学生进行一分钟跳绳次数测试，将所得数据整理后，图所示，图中左到右各小长方型的面积之比为小组频数为12．问：(1)(2)(3)求一分钟跳绳的众数，中位数和平均数．(4)若一分钟跳绳次数在110次以上（含110试估计该校全体高一学生的达标率是多少？【分析】(1)考查频率分布折线图与频率分布直方图的关系； (2)根据从左到右各小长方形的面积之比为 2:4:17:15:9:3，第二小组频数为12，用比值做出样本容量．做出的样本容量和第二小组的频率．(3)在频率分布直方图中最高的小长方形的底边的中点就是这组数据的众数的估计值，处在把频率分布直方图所有的小长方形的面积分成两部分的一条垂直与横轴的线对应的横标就是中位数的估计值，平均数的估计值是频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和．(4)根据上面做出的样本容量和前两个小长方形所占的比例，用所0.034 0.0180.03有的符合条件的样本个数之和，除以样本容量得到概率． 【解答】(1)如图所示(2)∵从左到右各小长方形的面积之比为 2:4:17:15:9:3，第二小组频数为12．∴样本容量是(24171593)121504+++++⨯=∴第二小组的频率是 120.08150=．(3)由图可知众数为1101201152+=，又∵前三个小矩形的面积之和为0.46．∴设中位数为120+x ，则0.460.030.5x +⨯=，得x =43，∴中位数为3643，而平均数为0.04950.081050.341150.31250.181350.06145121.8⨯+⨯+⨯+⨯+⨯+⨯=．(4)∵次数在110次以上（含110次）为达标，∴在这组数据中达标的个体数一共有17+15+9+3， ∴全体学生的达标率估计是1715930.8850+++=．【点评】本题考查频率分步直方图的应用，是一个基础题，这种题目解题的关键是看清图中所给的条件，知道小长方形的面积就是这组数据的频率． 变式训练:1.随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位:cm)，获得身高数据的茎叶图为如图(1)根据茎叶图判断哪个班的平均身高较高；用茎叶图分析数据的好处？(2)分别计算甲班、乙班的样本平均数及方差；(3)根据计算结果对两班的身高用其稳定性进行比较，写出统计结论． 答案：(1)由茎叶图不难看出乙班的平均身高较高；用茎叶图处理现有的数据不但可以看出数据的分布情况， 而且可以看出每组中的具体数据.(2)由茎叶图，得甲班的10名同学的身高分别为182 179 179 171 170 168 168 163 162 158甲班 乙班 18171615 3 73 6 8 9 2 5 8 99 9 1 0 2 8 8 3 2 8183 187 173 176 178 179 162 165 168 159， 得他们的平均身高为2173x cm =，22277.2s cm =．(3)由(2)的计算结果可以发现甲班的平均身高为170cm ，乙班的平均身高为173cm ．由此可知乙班的平均身高比甲班的平均身高高，但乙班的身高不够稳定，而甲班的身高比较集中在平均身高附近． 2.某次数学考试中，高一（20）班有20人成绩记录如下：（单位：分）125 121 123 125 127 129 125 128 130 129 126 124 125 127 126 122 124 125 126 128王老师想做出以上数据的频率分布直方图，他把这些数据分成5组，分组情况为[120.5,122.5)，[122.5,124.5)，[124.5,126.5)，[126.5,128.5)，[128.5,130.5]．(1)请你帮他完成频率分布直方图；(2)根据画出的直方图，求这组数据的众数、中位数、平均数． 答案：(1)略. (2) 众数为125.5，中位数为125.75，平均数为125.8． 小结：1.用样本频率分布估计总体频率分布时，通常要对给定的一组数据进行列表、作图处理，列表与作图时要注意其方法步骤；对于茎叶图要正确画图，能够根据图中所给的数据进行分析．2.在频率分布直方图中能够正确估计样本数据的众数、中位数、平均数，并且知道它们给分析数据带来的不同影响，不同的数字特征代表着不同的信息．由于需要不同信息而选择不同的数字特征，对同一组数据的评价可能会相差很大．3.会计算样本数据的方差、标准差，知道它们的作用；在实际应用中当所得数据平均数不同时，须先分析平均水平，再计算标准差（方差）分析稳定情况．例3．假设关于某设备的使用年限x 和所支出的维修费用y (万元)(1)性回归方程y bx a =+的回归系数 b ，a ；(2)估计使用年限为10年时的维修费用．【分析】(1)利用散点图可直接判断两变量是否线性相关；再利用公式1122211()(),()n niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑a y bx =-来计算回归系数．有时为了计算方便常制表对应求出2,,i i i x y x ，以利于求和．(2)获得线性回归方程后，取x =10即得所求． 【解答】(1)散点图如图所示： 由散点图可知两变量线性相关．于是有2112.3 1.23905410b -===-⨯，5 1.2340.08a y bx =-=-⨯=．(2)回归直线方程是 1.230.08y x =+，当x =10(年)时，1.23100.0812.38y =⨯+=(万元)，即估计使用10年时维修费用是12.38万元． 【点评】判断两变量是否线性相关一种简便可行的方法就是绘制散点图．根据散点图可以很容易看出两个变量是否具有相关关系．只有当两个变量之间存在线性相关关系时，才能用回归直线方程对总体进行估计和预测． 变式训练:1.小王记录了产量x （吨）和能耗y （吨标准煤）对应的四组数据，用最小二乘法求出了0.70.35y x =+，不慎将一滴墨水滴于表内，表中第二行第四列的数据已无法看清，据您判断这个数据应该是多少？答案：2.某数学老师身高176cm ，他爷爷、父亲和儿子的身高分别是173cm 、170cm 和182cm ．因儿子的身高与父亲的身高有关，该老师用线性回归分析的方法预测他孙子的身高是多少cm ？答案：185cm ． 小结：求线性回归直线方程应注意：先画散点图判断两变量是否线性相关；若线性相关，再利用公式计算,a b 的值，进而求出回归直线方程，但要注意运算顺序；然后就可以利用回归方程进行估计和预测． 四、【解法小结】1.对于随机抽样问题：掌握三种抽样方法的区别与联系，系统抽样的样本号码的特点以及分层抽样的比例的确定．2.应用频率分布直方图时，需明确纵轴表示的是频率/组距，进而进行相关计算．3.对于标准差、方差记准公式，知道其作用．4.掌握用最小二乘法求回归直线方程的步骤，注意运算顺序． 五、【布置作业】 必做题：1.(2012山东理高考)采用系统抽样方法从960人中抽取32人做问卷调查，为此将他们随机编号为 1,2,,960，分组后在第一组采用简单随机抽样的方法抽到的号码为9．抽到的32人中,编号落入区间 [1,450]的人做问卷A ，编号落入区间[451,750]的人做问卷B ，其余的人做问卷C ．则抽到的人中，做问卷B 的人数为_______________．2. (2012湖北文高考)一支田径运动队有男运动员56人，女运动员42人．现用分层抽样的方法抽取若干人,若抽取的男运动员有8人，则抽取的女运动员有_______________人.3.(2013山东文高考)将某选手的9个得分去掉1个最高分，去掉1个最低分，7个剩余分数的平均分为91分．现场作的9个分数的茎叶图后来有1个数据模糊，无法辨认，在图中以x 表示，则7个剩余分数的方差是_______________．4.(2011广东高考)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系，下表记录了小李某月1号到5号每天打篮球时间x法，预测小李该月6号打6小时篮球的投篮命中率为___________． 5.(2012广东文高考)某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是8 9 7 74 0 1 0 x 9 10.04 0.03 0.02[70,80)，[80，90)，[90，100]. (1)求图中a 的值；(2)根据频率分布直方图,估计这100名学生语文成绩的平均分； (3)若这100名学生的语文成绩某些分数段的人数x 与数学成绩 相应分数段的人数y 之比如下表所示,求数学成绩在[50，90) 之外的人数.6.某学校高一(3)班甲、乙两名同学的最近5次(1)(2)分别用平均数和中位数分析甲、乙两位同学中，哪位同学成绩较好；(3)(单位：分)如下：并说明理由．必做题答案：1.10 2. 6 3.3674. 0.5， 0.535. (1) a =0.005 (2)73 (3)106.(1)甲的平均分、中位数分别为90、95，乙的平均分、中位数分别为86、98；(2)从平均分看，甲的平均分高，甲的成绩较好；从中位数看，乙的中位数大，乙的成绩较好．(3)丙的平均数、中位数、方差分别为90、90、44.4，甲的方差为158.8．由于两人的平均分相同，所以从平均分看，甲、丙成绩同样好；从中位数看，甲的中位数高，甲的成绩高；从方差看，丙的方差小，丙的成绩较稳定，所以丙的成绩好． 选做题：(2012山西模拟)如下图，图甲是某市有关部门根据对当地干部的月收入情况调查后画出的样本频率分布直方图，已知图甲中从左向右第一组的频数为4000．在样本中记月收入在[1000,1500)，[1500,2000)，[2000,2500)，[2500,3000)，[3000,3500)，[3500，4000)的人数依次为A1，A2，…，A6．图乙是统计图中月工资收入在一定范围内的人数的程序框图，图乙输出的S＝______________．(用数字作答)．0.00080.00040.00030.000250.000150.0001。

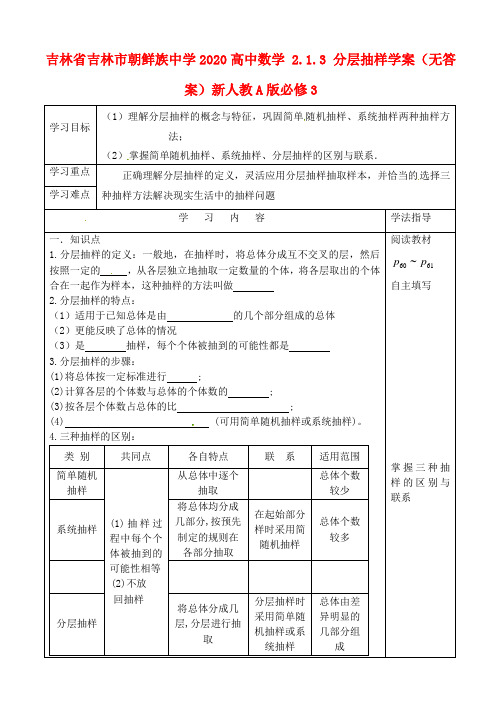
吉林省吉林市朝鲜族中学2020高中数学 2.1.3 分层抽样学案（无答案）新人教A版必修3学习目标（1）理解分层抽样的概念与特征，巩固简单随机抽样、系统抽样两种抽样方法；（2）掌握简单随机抽样、系统抽样、分层抽样的区别与联系．学习重点正确理解分层抽样的定义，灵活应用分层抽样抽取样本，并恰当的选择三种抽样方法解决现实生活中的抽样问题学习难点学习内容学法指导一．知识点1.分层抽样的定义：一般地，在抽样时，将总体分成互不交叉的层，然后按照一定的，从各层独立地抽取一定数量的个体，将各层取出的个体合在一起作为样本，这种抽样的方法叫做2.分层抽样的特点：（1）适用于已知总体是由的几个部分组成的总体（2）更能反映了总体的情况（3）是抽样，每个个体被抽到的可能性都是3.分层抽样的步骤：(1)将总体按一定标准进行 ;(2)计算各层的个体数与总体的个体数的 ;(3)按各层个体数占总体的比 ;(4) (可用简单随机抽样或系统抽样)。

4.三种抽样的区别：类别共同点各自特点联系适用范围简单随机抽样(1)抽样过程中每个个体被抽到的可能性相等(2)不放回抽样从总体中逐个抽取总体个数较少系统抽样将总体均分成几部分,按预先制定的规则在各部分抽取在起始部分样时采用简随机抽样总体个数较多分层抽样将总体分成几层,分层进行抽取分层抽样时采用简单随机抽样或系统抽样总体由差异明显的几部分组成阅读教材6160~pp自主填写掌握三种抽样的区别与联系二．典型例题例1：某班有男生36人,女生24人,从全班抽取一个容量为10的样本,分析某种身体素质指标,已知这种身体素质指标与性别有关. 问应采取什么样抽样方法？并写出抽样过程例2：某高中共有900人，其中高一年级300人，高二年级200人，高三年级400人，现采用分层抽样抽取容量为45的样本，那么高一、高二、高三各年级抽取的人数分别为( )A.15,5,25B.15,15,15C.10,5,30D.15,10,20 三．当堂检测1. 某单位有老年人28人，中年人54人，青年人81人，为了调查他们的身体情况，需从他们中抽取一个容量为36的样本，则适合的抽取方法是（）A、简单随机抽样 B、系统抽样C、分层抽样D、先从老人中剔除1人，然后再分层抽样2.某单位有职工160人，其中业务员有104人，管理人员32人，后勤24人，现用分层抽样从中抽取一容量为20的样本，则抽取管理人员（）人A、3B、4C、7D、123.某大学数学系共有本科生5000人，其中一、二、三、四年级的学生比为4：3：2：1，用分层抽样的方法抽取一个容量为200人的样本，则应抽取三年级的学生为（）人。

吉林省吉林市朝鲜族中学2020高中数学 3.1.2 概率的意义学案（无答案）新人教A版必修3学习目标1.理解概率的意义；2.能正确利用概率知识解决现实中的生活问题.学习重点利用概率知识解决现实中的生活问题学习难点利用概率知识解决现实中的生活问题学习内容学法指导一．知识点1.概率的正确理解：概率是描述随机事件发生的的度量，事件A的概率P(A)越大，其发生的可能性就越____；概率P(A)越小，事件A发生的可能性就越_______.2.概率的实际应用：知道随机事件的概率的大小,有利我们做出正确的 , 还可以某些决策或规则的正确性与公平性.3.游戏的公平性：应使参与游戏的各方的机会为等可能的, 即各方的相等, 根据这一要求确定游戏规则才是的.4.决策中的概率思想：以使得样本出现的最大为决策的准则.5.天气预报的概率解释：降水的概率是指降水的这个随机事件出现的 , 而不是指某些区域有降水或能不能降水.6.遗传机理中的统计规律:利用遗传定律，帮助理解概率统计中的随机性与的关系，以及频率与的关系。

二．典型例题题型一概率的意义例1. 经统计某篮球运动员的投篮命中率是90%，对此有人解释为其投篮100次一定有90次命中，10次不中，你认为正确吗？题型二游戏的公平性判断例2.在乒乓球，排球等比赛中，裁判员都用哪些方法决定谁先发球？这些方法公平吗？例如：通过掷硬币或抽签的方法，决定谁先发球，这两种方法公平吗？那么使用猜拳的方法呢？题型三概率的应用例3. 某人进行打靶练习，共射击10次，其中有2次阅读教材118113~pp自主填写概率是描述随机事件发生的可能性大小的度量。

注意频率与概率的关系中10环，有3次环中9环，有4次中8环，有1次未中靶，试计算此人中靶的频率，假设此人射击1次，试问中靶的概率约为多少？中9环的概率约为多少？三．当堂练习1．下列说法正确的是（）A、某事件发生的频率为p(A)=1.1；B、不可能事件的概率为0，必然事件的概率为1；C、小概率事件就是不可能发生的事件，大概率事件就是必然要发生的事件；D、某事件发生的概率是随着试验次数的变化而变化的。

1．若0a >，且,m n 为整数，则下列各式中正确的是 （ ）A m m n n a a a ÷=B n m n m a a a •=•C ()n m m n a a +=D 01n n a a -÷=2.有以下四个结论 ① l g(l g10)=0 ② l g(l n e )=0 ③若10=l g x ,则x=10 ④ 若e =ln x,则x =e 2, 其中正确的是 （ ）A. ① ③B.② ④C. ① ②D. ③ ④3.已知10<<a ，0log log <<n m a a ，则 （ ）A m n <<1B n m <<1C 1<<n mD 1<<m n4．函数22log (1)y x x =+≥的值域为 （ ）A ()2,+∞B (),2-∞C [)2,+∞D [)3,+∞5．设 1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭，则 （ ） A 312y y y >> B 213y y y >> C 132y y y >> D 123y y y >>6.计算lg52lg2)lg5()lg2(22•++等于 （ ）A 0B 1C 2D 37.已知3log 2a =，那么33log 82log 6-用a 表示是 （ ）A 52a -B 2a -C 23(1)a a -+D 231a a -- 8.函数log (2)1a y x =++的图象过定点 （ ）A.（1，2）B.（2，1）C.（-2，1）D.（-1，1）9.函数y= | lg （x-1）| 的图象是 （ ）10.函数265y x x =---的值域为 （ ）A []0,2B []0,4C (],4-∞D [)0,+∞11.已知不等式为27331<≤x ，则x 的取值范围（A ）321<≤-x （B ）321<≤x （C ）R （D ）3121<≤x 12.函数12+=-x a y (0>a ，且1≠a )的图象必经过点(A)(0，1) (B)(1，1) (C) (2， 0) (D) (2，2)13. 函数y ＝log 2x ＋3（x≥1）的值域是 ; 函数21()log (2)f x x =-的定义域是 ．14．已知幂函数的图像经过点（2，32）则它的解析式是 .15．试比较2212208090log 71...., ., .的大小关系,并按照从小到大的顺序排列是16．函数)x 2x (log y 221-=的单调递减区间是_______________．17．求下列函数的定义域：（1）3)1(log 1)(2-+=x x f （2）2log 2-=x y18.计算：（1） ()[]2175.034303101.016254064.0++-+⎪⎭⎫ ⎝⎛-----（2）21log 31324lg 22493+-19.已知函数xx x f -+=11lg)(，（1）求)(x f 的定义域； （2）使0)(>x f 的x 的取值范围.。