浙江省桐庐分水高级中学2013届高三上学期第二次阶段性教学质量检测数学理试题

高中数学学习材料鼎尚图文*整理制作高2013级高三第二次诊断性测试数 学（文史类）本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）．第Ⅰ卷1至2页，第Ⅱ卷3至4页．考生作答时，须将答案答在答题卡上，在本试卷、草稿纸上答题无效．满分150分，考试时间120分钟. 考试结束后，将本试题卷和答题卡一并交回.第Ⅰ卷（选择题，共50分）注意事项：必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑．一、选择题:本大题共10个小题,每小题5分,共50分；在每小题给出的四个选项中,只有一项是符合题目要求的.1．设集合{}11A x x =-≤≤，{}03B x x =<<，则A B =I(A) {}01x x <≤ (B) {}01x x << (C) {}13x x -≤< (D) {}13x x ≤< 2．在复平面内，复数31i 1i++对应的点位于 （A ）第一象限（B ）第二象限 （C ）第三象限 （D ）第四象限3．2016年3月“两会”期间，有代表提出适当下调“五险一金”的缴存比例，现拟从某工厂职工中抽取20名代表调查对这一提案的态度，已知该厂青年，中年，老年职工人数分别为350，500，150，按分层抽样的方法，应从青年职工中抽取的人数为(A) 5 (B) 6 (C) 7 (D) 104．下列函数中，最小正周期为π且图象关于y 轴对称的函数是(A) cos(2)2y x π=+(B) sin y x =(C) 2sin ()4y x π=-(D) sin 2cos 2y x x =+5．执行如图所示的程序框图，若输入x 的值为5-，则输出y 的值是(A) －1 (B) 1 (C) 2 (D) 146．已知函数2()x f x a-=，()log a g x x =（其中0a >且1a ≠），若(5)(3)0f g ⋅->，则()f x ，()g x 在同一坐标系内的大致图象是(A) (B) (C) (D)7．已知直线2100x y +-=过双曲线22221(0,0)x y a b a b-=>>的焦点且与该双曲线的一条渐近线垂直，则该双曲线的方程为(A)221169x y -= (B)221205x y -= (C) 221520x y -= (D) 221916x y -= 8．设52()ln(1)f x x x x =+++，则对任意实数a ，b ，“0a b +≥”是“()()0f a f b +≥”的(A) 充分不必要条件 (B) 必要不充分条件 (C) 充要条件(D) 既不充分也不必要条件9．设实数x ，y 满足约束条件324040120x y x y x y a ⎧⎪-+≥⎪+-≤⎨⎪⎪--≤⎩，已知2z x y =+的最大值是7，最小值是26-，则实数a 的值为(A) 6 (B) 6- (C) 1-(D) 110.已知抛物线2:4C y x =的焦点为F ，它的准线与对称轴的交点为,H 过点H 的直线与抛物线C 交于A B 、两点，过点A 作直线AF 与抛物线C 交于另一点1B ，过点1A B B 、、的圆的圆心坐标为,a b （），半径为r ，则下列各式成立的是(A) 2214a r =-(B) a r = (C) 2214a r =+(D) 221a r =+第Ⅱ卷（非选择题，共100分）注意事项：必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答．作图题可先用铅笔绘出，确认后再用0.5毫米黑色墨迹签字笔描清楚．试题卷上作答无效.二、填空题：本大题共5小题，每小题5分，共25分.11．计算：51log 25lg ln 100e ++= .12．已知等腰三角形ABC 的底边AB 的长为4，则AC AB ⋅= .13．已知βα,3(,)4ππ∈，4cos()5αβ+=，5cos()413πβ-=-,则sin()4πα+=________.14．某三棱锥的正视图，侧视图，俯视图如图所示，则该三棱锥的表面积是 .15．若存在实数0x 和正实数x ∆，使得函数)(x f 满足00()()4f x x f x x +∆=+∆，则称函数)(x f 为“可翻倍函数”，则下列四个函数 ① ()f x x =； ②2()2,[0,3]f x x x x =-∈；③()4sin f x x =； ④ ()ln x f x e x =-. 其中为“可翻倍函数”的有 （填出所有正确结论的番号）.三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤．不能答试卷上，请答在答题卡相应的方框内.16．(本小题满分12分)已知等比数列{}n a 的各项均为正数，且21231761,9a a a a a +==.（Ⅰ）求数列{}n a 的通项公式； （Ⅱ）设3132333log log log log n n b a a a a =++++，求数列1n b ⎧⎫⎨⎬⎩⎭的前n 项和n S .17．(本小题满分12分)某人设置一种游戏，其规则是掷一枚均匀的硬币4次为一局，每次掷到正面时赋值为1，掷到反面时赋值为0，将每一局所掷4次赋值的结果用(,,,)a b c d 表示，其中,,,a b c d 分别表示掷第一、第二、第三、第四次的赋值，并规定每局中“正面次数多于反面次数时获奖”. （Ⅰ）写出每局所有可能的赋值结果； （Ⅱ）求每局获奖的概率；（Ⅲ）求每局结果满足条件“+++2a b c d ≤”的概率. 18．（本小题满分12分）在ABC ∆中，内角,,A B C 所对的边分别为,,a b c ，若()()a b c a b c bc +--+=. （Ⅰ）求A 的值；（Ⅱ）已知向量m (,31)c =+,n (,2)b =,若m 与n 共线，求tan C .19．（本小题满分12分）如图，在四棱锥O ABCD -中，底面ABCD 是边长为2的正方形，侧棱OB ⊥底面ABCD ，且侧棱OB 的长是2，点,,E F G 分别是,,AB OD BC 的中点. （Ⅰ）证明：EF //平面BOC ； （Ⅱ）证明:OD ⊥平面EFG ； （Ⅲ）求三棱锥G EOF -的体积.20．（本小题满分13分）已知椭圆Γ：22221(0)x y a b a b +=>>的离心率等于22，椭圆Γ上的点到它的中心的距离的最小值为2.（Ⅰ）求椭圆Γ的方程；（Ⅱ）过点(0,4)E 作关于y 轴对称的两条直线分别与椭圆Γ相交，y 轴左边的交点由上到下依AD B C OEFG次为A B ,，y 轴右边的交点由上到下依次为,C D ，求证：直线AD 过定点，并求出定点坐标.21．(本小题满分14分)已知函数()2xf x me x =--.（其中e 为自然对数的底数）.（Ⅰ）若曲线()y f x =过点(0,1)P ，求曲线()f x 在点(0,1)P 处的切线方程； （Ⅱ）若()0f x >在R 上恒成立，求m 的取值范围；（Ⅲ）若()f x 的两个零点为12,x x ，且12x x <，求21211()()x xx x y e e m e e=--+的值域.高2013级高三第二次诊断性测试数学(文史类)参考答案说明：一、本解答给出了一种解法供参考，如果考生的解法与本解答不同，可比照评分意见制订相应的评分细则．二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半，如果后继部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数，选择题和填空题不给中间分． 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 答案ADCBACBCDD二、填空题 11.12 12.8 13.3365- 14.4+3 15. ①④ 三、解答题16.解：（Ⅰ）设等比数列公比为为q ,因各项为正,有0q > …………………….…（1分）由1121122426317111616139913a a a a a q a a a a q a q q ⎧=⎪+=+=⎧⎧⎪⇒⇒⎨⎨⎨==⎩⎩⎪=⎪⎩……………………………….…（5分） 1()3n n a ∴= (n *∈N ) …………………………………………….…. …（6分）（Ⅱ）n n a a a a b 3332313log log log log ++++= 312log ()n a a a =⋅⋅⋅⋅⋅⋅12+31log ()3n++= (1)2n n +=-…………………………………………………...（9分） 12112()(1)1n b n n n n ∴=-=--++………………………………………….…（10分） ∴⎭⎬⎫⎩⎨⎧n b 1的前n 项和12111111111+212231n n S b b b n n ⎡⎤⎛⎫⎛⎫⎛⎫=++=--+-++- ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦21n n =-+…（12分） 17.解：（Ⅰ）每局所有可能的赋值结果为：(1,1,1,1)， (1,1,1,0)，(1,1,0,1)，(1,1,0,0)，(1,0,1,1)，(1,0,1,0)，(1,0,0,1)，(1,0,0,0)，(0,1,1,1)， (0,1,1,0)，(0,1,0,1)，(0,1,0,0)，(0,0,1,1)，(0,0,1,0)，(0,0,0,1)，(0,0,0,0) ……………………………..…（4分）（Ⅱ）设每局获奖的事件为A ，以（Ⅰ）中结果为基本事件，A 所含的基本事件有5个，∴每局获奖的概率P A =（）516………………………………………..………（8分） （III ）设满足条件“+++2a b c d ≤”的事件为B ，由（Ⅰ）知B 所含的的基本事件有11个，∴ P B （）=1116…………………………………………..…..（12分） 法2：+++2a b c d ≤⇔所掷4次中至多2次正面向上，为（Ⅱ）中A 的对立事件A ，∴ 51111616P A =-=（） 18.解: （Ⅰ）()()a b c a b c bc +--+=∴2222a b c bc bc --+=∴222b c a bc +-= ………………………………………..(3分) 由余弦定理知：2222cos b c a bc A +-= ………………..…(5分)∴1cos2A = 0A π<<∴ 3A π=…………………………….(6分)（Ⅱ）m 与n 共线∴ 2(31)c b =+ ……………………………...(7分)由正弦定理知：2sin (31)sin C B =+ …………….………...(8分) 又在ABC ∆中， sin sin()B A C =+∴2sin (31)sin()3C C π=++ ……………………………………..(10分)即：312sin (31)(cos sin )22C C C =++ (33)sin (33)cos C C -=+∴tan 23C =+ ………………………………………….（12分）19.（Ⅰ）证明：作OC 的中点H ,连接,FH BH ,,F H 分别是,OD OC 的中点 ∴FH //12CD ……………………………………………………(1分) 又在正方形ABCD 中，E 是AB 的中点,∴EB //12CD …………………………………………………………（2分）∴EB //FH∴四边形BEFH 是平行四边形∴//EF BH ,又EF ⊄平面BOC ，BH ⊂平面BOC∴EF //平面BOC ………………………………………………(4分) （Ⅱ）证明:四边形ABCD 是边长为2的正方形，E 是AB 的中点,∴5DE =又侧棱OB ⊥底面ABCD ,AB ⊂面ABCD ∴OB ⊥AB又2,1OB EB ==∴5OE =∴5,DE OE ==∴ODE ∆是等腰三角形， F 是OD 的中点,∴EF OD ⊥ ………………………………………….……………..(5分) 同理5,DG DG ==∴ODG ∆是等腰三角形， F 是OD 的中点,FG OD ∴⊥ ……………………………………………………….（6分） EF FG F = ,EF FG ⊂面EFGOD ⊥平面EFG ……………………………………………………(8分)（Ⅲ）解:侧棱OB ⊥底面ABCD ,BD ⊂面ABCD∴OB ⊥BD2,22OB DB ==∴23OD =由（Ⅱ）知：OD ⊥平面EFGOF 是三棱锥O 到平面EFG 的距离 F 分别是OD 的中点3OF = …………………………………………………………(9分)5,DE OE ==EF OD ⊥, ∴2EF =5,DG DG ==FH OD ⊥∴2FG =四边形ABCD 是边长为2的正方形，,E G 是,AB BC 的中点AD BC OEFGH∴2EG =∴三角形EFG 是等边三角形∴32EFG S = ……………………………………………………………（11分）01132G EOF EFG V V Sh --=== …………………………………………（12分）20.解：（Ⅰ）由已知222222c a b a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩， ……………………………………………..……（2分）得222a b ⎧=⎪⎨=⎪⎩， 椭圆Γ的方程为22184x y += ……………..…（4分） （Ⅱ）证明：由已知可设AB 方程为4(0),y kx k =+>代入22184x y += 得22(12)16240k x kx +++=………………………………………..……（5分）设1122(,),(,)A x y B x y ，则1212221624,1212k x x x x k k+=-=++.…..……（6分） 由对称性知22(,)D x y -，AD ∴方程为121112(),y y y y x x x x --=-+.……（8分）11224,4y kx y kx =+=+，AD ∴方程可化为121112()()4k x x y x x kx x x -=-+++……………………………………..……（9分）1212111212()()4k x x k x x x x kx x x x x --=-++++2122121121212224()2()124241612k x x x k x x k x kx x k k x x x x x x k --+=++=+⨯++++-+1212()1k x x x x x -=++ …………………………………………………..……（12分）AD ∴恒过定点，定点为(0,1)……………………………………………..……（13分）其它证法，参照给分。

桐庐分水高级中学2013届高三上第二次阶段性质检数学理试题时间：120分钟 分值：150分一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{}023>+=x x A ，{}0)3)(1(>-+=x x x B ，则=B A （ ）A ．)1,(--∞B ．⎭⎬⎫⎩⎨⎧--32,1C ．)3,32(-D ．),3(+∞ 2．“4m =-”是“直线820mx y +-=与直线210x my +-=平行”的（ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ． 既不充分又非必要条件3．:①a b ab +<;③a b <;（ ）A ．①②B ．②③C ．①④D ．③④ 4．已知等差数列}a {n 的公差为2，若431a ,a ,a 成等比数列，则1a =（ ） A ．－4B ．－8C ．－6D ．－105．若圆03222=+-+by ax y x 的圆心位于第三象限，则直线0=++b ay x 一定不经过第（ ）象限A ．四B ．三C ．二D ．一 6．若||1,||2,a b c a b ===+，且c a ⊥，则向量a 与b 的夹角为 ( ) A ．30° B ．60° C ．120° D ．150°7．在区间],[n m 上有最大值10，则函数)(x f 在区间],[m n --上有( )A. 最大值-10B. 最小值-10C. 最小值—26D. 最大值-26 8．等比数列{}n a 的各项均为正数，且564718a a a a +=，则3132310lo g lo g lo g a a a ++=（ ） A ．12B ．10C ．8D ．32log 5+9 ） A.2B.3C.4D.510．已知函数)0()(23≠+++=a d cx bx ax x f 的对称中心为00(,)M x y ，记函数)(x f 的导函数为)(/x f ，)(/x f 的导函数为)(//x f ，则有0)(0//=x f .若函数()323f x x x =-，） A ．4023 B ．4023- C ．8046 D ．8046-二、填空题：本大题共7小题，每小题4分，共28分。

浙江杭高2013届高三第二次月考数学（理）试题注意事项：1．本试卷考试时间为120分钟，满分为150分，不得使用计算器； 2．答案一律做在答卷页上．一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1． 设集合{}{}1log ,0122<=>-=x x B x x A ，则B A 等于 A ．{|1}x x <- B ．{}20<<x xC ．{}21<<x xD ．{|121}x x x <<<-或2． 函数)56(log )(221+-=x x x f 的单调递减区间是A ．(,3)-∞B ．(3,)+∞C ．(,1)-∞D ．(5,)+∞3． 以下有关命题的说法错误的是A ．命题“若0232=+-x x ,则1=x ”的逆否命题为“若1≠x ，则0232≠+-x x ”B ．“1=x ”是“0232=+-x x ”的充分不必要条件C ．若q p ∧为假命题，则q p 、均为假命题D ．对于命题R x p ∈∃:使得012<++x x ，则R x p ∈∀⌝:，均有012≥++x x 4． 已知函数)0,0,0)(cos()(πϕωϕω<<>>+=A x A x f 为奇函数，该函数的部分图象如图所示，EFG ∆是边长为2的等边三角形，则)1(f 的值为A ．23-B ．26-C ．3D ． 3-5．函数xxa y x=(01)a <<的图象的大致形状是6． 定义在R 上的函数)(x f y =满足)()5(x f x f -=+，0)()25(/>-x f x ，已知21x x <，则)()(21x f x f >是521<+x x 的（ ）条件．A ．充分不必要B ．必要不充分C ．充分必要D ．既不充分也不必要7． 已知非零向量a ，b 满足|a + b | =|a –b a |，则a + b 与a –b 的夹角为A ． 30︒B ．60︒C ．120︒D ．150︒8． 已知二次函数2()1f x ax bx =++的导函数为()f x '，(0)0f '>，f （x ）与x 轴恰有一个交点，则(1)(0)f f '的最小值为A ． 2B ．32C ． 3D ．529． 当x ∈（－2，－1）时，不等式（x+1）2<log a |x|恒成立，则实数a 的取值范围是 A ．[2,+∞） B ．（1,2] C ．（ 1,2） D ．（0,1） 10． 已知函数()f x 满足：()114f =，()()()()()4,f x f y f x y f x y x y R =++-∈，则()2010f =A ．12B ．13C ．14D ．1二、填空题：本大题共7小题，每小题4分，共28分． 11． 已知53)4sin(=-x π，则x 2sin 的值为 12． 函数)cos lg(sin )(22x x x f -=的定义域是_______________ 13． 已知函数x ax x x f 331)(23++=在（0， 1）上不是单调函数，则实数a 的取值范围为 _____14． 已知在平面直角坐标系中，O B A ),3,1(),0,2(-为原点，且,OB OA OM βα+=（其中1,,αβαβ+=均为实数），若N （1，0），则||MN 的最小值是15．如图，在平行四边形ABCD 中 ，AP ⊥BD ，垂足为P ，3AP =且AP AC =16． 若函数y =)1(log 2+-ax x a 有最小值，则a 的取值范围是________17． 已知)3)(2()(++-=m x m x m x f ，22)(-=xx g ，若R x ∈∀，0)(<x f 或0)(<x g ，则m 的取值范围是_________三、解答题：本大题共5小题，共72分．解答应写出文字说明，证明过程或演算步骤． 18．（本题满分14分） 来已知等差数列{}n a 满足：37a =，5726a a +=．{}n a 的前n 项和为n S ．（Ⅰ）求n a 及n S ；（Ⅱ）令211n n b a =-（n N +∈）,求数列{}n b 的前n 项和n T ．19． （本题满分14分）[来已知函数21()cos cos ,2f x x x x x R =--∈． （1） 求函数)(x f 的最小值和最小正周期；（2）已知ABC ∆内角A B C 、、的对边分别为a b c 、、，且3,()0c f C ==，若向量(1,sin )m A =u r 与(2,sin )n B =r共线，求a b 、的值．20．（本题满分14分） 已知点O 为ABC ∆的外心，角A ，B ，C 的对边分别为a ，b ，c 。

2013年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题1．已知i 是虚数单位，则=-+-)2)(1(i iA ．i +-3 B. i 31+- C. i 33+- D.i +-1 2．设集合}043|{},2|{2≤-+=->=x x x T x x S ，则=⋃T S C R )( A ．(2,1]- B. ]4,(--∞ C. ]1,(-∞ D.),1[+∞ 3．已知y x ,为正实数，则A.y x y x lg lg lg lg 222+=+B.lg()lg lg 222x y x y+=⋅ C.lg lg lg lg 222x yx y ⋅=+ D.lg()lg lg 222xy x y =⋅ 4．已知函数),0,0)(cos()(R A x A x f ∈>>+=ϕωϕω，则“)(x f 是奇函数”是2πϕ=的A ．充分不必要条件 B. 必要不充分条件C. 充分必要条件D.既不充分也不必要条件 5．某程序框图如图所示，若该程序运行后输出的值是59，则 A.4=a B.5=a C. 6=a D.7=a6．已知210cos 2sin ,=+∈αααR ，则=α2tan A.34 B. 43C.43-D.34-7．设0,P ABC ∆是边AB 上一定点，满足AB B P 410=，且对于边AB 上任一点P ，恒有（第5题图）00PB PC P B PC ⋅≥⋅。

则 A. 090=∠ABC B. 090=∠BAC C. AC AB = D.BC AC = 8．已知e 为自然对数的底数，设函数)2,1()1)(1()(=--=k x e x f k x ，则A ．当1=k 时，)(x f 在1=x 处取得极小值B ．当1=k 时，)(x f 在1=x 处取得极大值C ．当2=k 时，)(x f 在1=x 处取得极小值D ．当2=k 时，)(x f 在1=x 处取得极大值9．如图，21,F F 是椭圆14:221=+y x C 与双曲线2C 的公共焦点，B A ,分别是1C ，2C 在第二、四象限的公共点。

浙江省杭州市2013届高三第二次教学质检检测数学（理）试题一、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知i 是虚数单位，则11i ii i++=+（ ） A ．1322i -+ B ．1322i - C ．3122i + D ．3122i - 2．已知集合{|sin()sin ,(0,)},{|cos()cos ,2A k Z kB k Z k pp q q q p q q q =?=??=(0,)},()2z A B p= 则ð（ ）A ．{|2,}k k n n Z =B ．{|21,}k k n n Z =-C ．{|4,}k k n n Z =D ．{|41,}k k n n Z =- 3．设P 为函数()sin()f x x p =的图象上的一个最高点，Q 为函数()cos()g x x p =的图象上的一个最低点，则|PQ|最小值是（ ）AB ．2 CD ．4．设直线：:(0)l y kx m m =+ ，双曲线2222:1(0,0)x y C a b a b+=>>，则“b k a =-”是“直线l 与双曲线C 恰有一个公共点“的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分条件D ．既不充分也不必要条件5．若存在实数x ，y 使不等式组0320,60x y x y x y ì- ïïï-+ íïï+- ïïî与不等式20x y m -+ 都成立，则实数m 的取值范围是（ ）A ．m≥0B ． m≤3C ．m≥lD ．m≥36．设数列{a n }是首项为l 的等比数列，若11{}2n n a a ++是等差数列，则12231111()()22a a a a +++2012201311()2a a +++ 的值等于（ ） A ． 2012B ． 2013C ． 3018D ． 30197．已知双曲线2222:1(0,0)y x C a b a b+=>>，A ，B 是双曲线的两个顶点．P 是双曲线上的一点，且与点B在双曲线的同一支上．P 关于y 轴的对称点是Q 若直线AP ，BQ 的斜率分别是k 1，k 2，且k 1·k 2=45-，则双曲线的离心率是（ ）A．5B ．94C ．32D ．958．若函数()(1).xf x x e =+，则下列命题正确的是（ ）A ．对任意21m e <-，都存在x R Î,使得()f x m < B ．对任意21m e >-，都存在x R Î，使得()f x m < C ．对任意21m e <-，方程()f x m =只有一个实根 D ．对任意21m e>-，方程()f x m =总有两个实根9．在直角坐标中，A （3，1），B （－3，－3），C （l ．4）．P 是AB 和AC夹角平分线上的一点，且AP =2，A ．()1313- B ．(-C ．(55-D (-10．如图，平面a 与平面b 交于直线l ，A ，C 是平面a 内 不同的两点，B ，D 是平面b 内不同的两点，且A ，B ． C ．D 不在直线l 上，M ，N 分别是线段AB ，CD 的中点，下列判断正确的是（ ）A ．若AB 与CD 相交，且直线AC 平行于l 时，则直线BD与l 可能平行也有可能相交B ．若AB ，CD 是异面直线时，则直线MN 可能与l 平行C ．若存在异于AB ，CD 的直线同时与直线AC ，MN ，BD都相交，则AB ，CD 不可能是异面直线D ．M ，N 两点可能重合，但此时直线AC 与l 不可能相交 二、填空题（本大题共7小题，每小题4分，共28分）11．已知2cos ()3x x R =，则cos()3x p-= 。

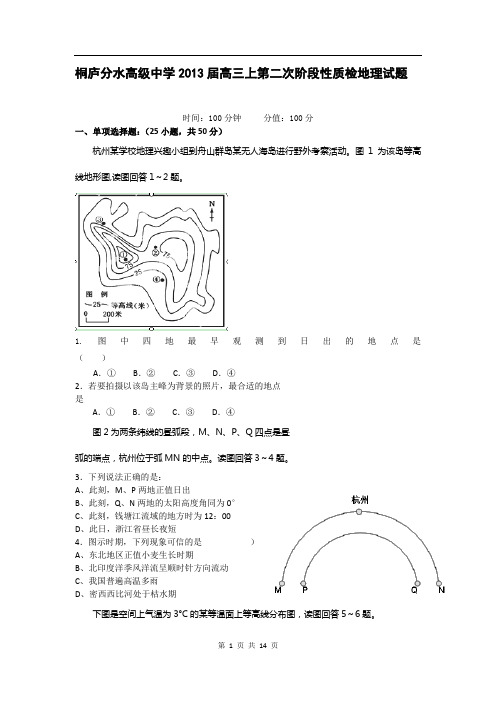
桐庐分水高级中学2013届高三上第二次阶段性质检地理试题时间：100分钟分值：100分一、单项选择题：（25小题，共50分）杭州某学校地理兴趣小组到舟山群岛某无人海岛进行野外考察活动。

图1为该岛等高线地形图,读图回答1～2题。

1.图中四地最早观测到日出的地点是（）A．①B．②C．③D．④2．若要拍摄以该岛主峰为背景的照片，最合适的地点是A．①B．②C．③D．④图2为两条纬线的昼弧段，M、N、P、Q四点是昼弧的端点，杭州位于弧MN的中点。

读图回答3～4题。

3．下列说法正确的是：A、此刻，M、P两地正值日出B、此刻，Q、N两地的太阳高度角同为0°C、此刻，钱塘江流域的地方时为12：00D、此日，浙江省昼长夜短4．图示时期，下列现象可信的是）A、东北地区正值小麦生长时期B、北印度洋季风洋流呈顺时针方向流动C、我国普遍高温多雨D、密西西比河处于枯水期下图是空间上气温为3°C的某等温面上等高线分布图，读图回答5～6题。

5．从热力环流原理看图示近地面：A．①为海洋④陆地B．①为谷地④为山地C．①郊区④为城区D．①为陆地④为海洋6．若图示近地面地势低平，气温都为21．5°C则飞机在图中①、②、③、④四处飞行时飞行员感觉最颠簸的是：A．①B．②C．③D．④下图是世界某区域的经纬网，图中箭头为地球自转方向，阴影为黑夜，此时在丙地正好可以看到日落的景观，读图完成第7题。

7．若此刻丙地是17：30，此时有一架飞机从乙地取最短路径飞往甲地，行程用了2小时30分钟，则下列说法正确的是A．飞机先向东北后向东南飞B．飞机先向东南后向东北飞C．抵达甲地时，当地时间为当日18：00D．抵达甲地时，当地时间为当日20时读河曲及河床剖面图图，回答8～9题：8．右侧的四幅图是沿M-N的河床剖面图。

能正确表示河床和水流特征的是A．A B．B C．C D．D9．以下关于这种河段的叙述，正确的是A．若水流方向与图示相反，则N岸侵蚀，M岸堆积B．这种特征的河流多分布在崎岖的山区C．这种特征的河流河面宽阔，水流平稳，非常有利于航行D．其发展趋势是越来越弯曲，最后突然变直10、图中气压带和风带由南向北排序正确的是A、②①③④B、②③①④C、④③①②D、④①③②11.有关图示气压带和风带的叙述，正确的是A、长江中下游地区的伏旱天气与气压带M无关B、南亚夏季风的形成与风带c的北移有关C、风带a和c之间的区域终年温和湿润D、气压带M和风带b交替控制下形成热带草原气候某校地理研究性学习小组分析了各种气候类型的成因与分布关系，并进行了各种模拟演示，读图回答12～13题：12.当黄赤交角为0°时，该小组在模拟演示中发现M地气候类型在地球上无法再找到。

浙江省杭州市桐庐分水高级中学高二数学测试（7）班级________ 姓名________ 得分一、选择题（每小题4分，共40分）1）ABCD2．如果角θ的终边经过点，则=θtan （ ）3．在平面直角坐标系中，已知(1,2)A -，(3,0)B ，那么线段AB 中点的坐标为（ ）A ．(2,1)-B ． (2,1)C ．(4,2)-D ．(1,2)-4．在三角形ABC 中,若AB=2,AC=3,角A= 060,则BC 的长为（ ）C.35．过点（－1，3）且垂直于直线x －2y+3=0的直线方程为（ ）A.2x+y －1=0B.2x+y －5=0C.x+2y －5=0D.x －2y+7=06．已知函数))(2sin(2)(R x x x f ∈-=π，下列结论错误的是 （ ）A.函数)(x f 的最小正周期为π2B. 函数)(x f 在区间],0[π上是增函数C. 函数)(x f 的图像关于直线0=x 对称D. 函数)(x f 是奇函数 7．如图，一个空间几何体的主视图、左视图、俯视图均为全等的等腰直角三角形，且直角三角形的直角边长为1，那么这个几何体的体积为（ ）A ．16B ．13C ．12D ．1 8.设α，β为不重合的平面，m ，n 为不重合的直线，则下列命题正确的是( )A ．若m ⊂α，n ⊂β，m ∥n ，则α∥βB ．若n ⊥α，n ⊥β，m ⊥β，则m ⊥αC ．若m ∥α，n ∥β，m ⊥n ，则α⊥βD ．若α⊥β，n ⊥β，m ⊥n ，则m ⊥α9．在正方体1111ABCD A B C D -中,E 为线段11AC 的中点,则异面直线DE 与1BC 所成的角的大小 （ ）主视图 左视图俯视图A.15度B.30度C. 45度D.60度10.已知点P 在直线x ＋3y －1＝0上，点Q 在直线x ＋3y ＋3＝0上，PQ 中点为M (x 0，y 0)，且y 0≥x 0＋2，则y 0x 0的取值范围为( ) A. 11,37⎛⎫-- ⎪⎝⎭ B.11,,37⎛⎤⎡⎫-∞-⋃-+∞ ⎪⎥⎢⎝⎦⎣⎭ C.11,37⎛⎤- ⎥⎝⎦D. 11,37⎛⎤-- ⎥⎝⎦二、填空题（每小题4分，共20分）11. .已知圆C 的圆心为（1，-2），半径为3的圆的标准方程为 ；12.点A （1,2）到直线y=2x-1的距离为： ；13．函数f (x )＝2cos 2x －3sin2x (x ∈R )的最小正周期是 ；f (x )的最大值为 ；14．已知函数k x A x f ++=)sin ()(φω（2,0πφω≤>）图象一部分如图所示，则函数的解析式为 .15．若直线m 被两平行线12:10:30l x y l x y -+=-+=与所截得的线段的长为22，则m 的倾斜角可以是 ①15 ②30 ③45 ④60 ⑤75其中正确答案的序号是 .（写出所有正确答案的序号）三、解答题（共40分）16．（8）求经过直线0323:,0532:21=--=-+y x l y x l 的交点且平行于直线032=-+y x 的直线方程.17．（5+6+7）如图，ABCD 是正方形，O 是该正方形的中心，P 是平面 ABCD 外一点，PO ⊥底面 ABCD ，E 是 PC 的中点．求证：(1)PA ∥平面 BDE ；(2)平面BDE ⊥平面 PAC .（3）若2,2==PO AB ，求AP 与平面ABCD 所成角的正切值。

桐庐分水高级中学2013届高三上第二次阶段性质检化学试题时间：90分钟分值：100分本卷可能用到的相对原子质量H—1 C—12 N—14 O—16 Cu—64 Na—23 Fe—56一、选择题（下列每小题只有一个选项符合题意。

共24小题，每题2分，共48分）1．化学已渗透到人类生活的各个方面。

下列说法正确的是A．光导纤维导电能力很强，是一种很好的通讯材料B．氢氧燃料电池、纽扣电池、硅太阳能电池都利用了原电池原理C．在入海口的钢铁闸门上装一定数量的铜块可防止闸门被腐蚀D．禁止使用四乙基铅作汽油抗爆震剂，可减少汽车尾气污染2．通过复习总结，你认为下列对化学知识概括合理的是A．金属氧化物都是强电解质B．一种元素可能有多种氧化物，但同种化合价只对应一种氧化物C．在化学反应中，一定有化学键的断裂和形成，并伴有能量的变化D．能与金属镁反应产生氢气的溶液一定是酸溶液3．将足量CO2气体通入水玻璃(Na2SiO3水溶液)中，然后加热蒸干，再在高温下充分灼烧，最后得到的固体物质是A．Na2SiO3B．Na2CO3、Na2SiO3C．Na2CO3、SiO2D．SiO2 4．下列化学用语使用正确的是A．F－离子的结构示意图：B．水分子的球棍模型：C．HCN分子的结构式：H—C≡N D．二氧化碳的电子式5．N A代表阿伏加德罗常数，下列说法正确的是A．7gCnH2n中含有的氢原子数目为N AB．18 g D2O中含有的质子数目为10NAC．标准状况下，22.4LCHCl3中含有氯原子数目为3N AD．1 L0.5mol/LNa2CO3溶液中含有的CO32－数目为0.5NA6．下列反应的离子方程式正确的是A．Ba(OH)2溶液中加入少量KAl(SO4)2溶液：3Ba2＋+6OH－+2Al3＋+3SO42－=BaSO4↓+2Al(OH)3↓B．FeCl3溶液中加入过量Na2S溶液：2Fe3＋+S2－= 2Fe2＋+S↓C．将适量SO2通入Ca(ClO)2溶液中Ca2＋+2ClO－+SO2+H2O= CaSO3 ↓+2HClOD．向Ca(OH)2溶液中加入过量的NaHCO3溶液Ca2＋+2HCO3－+2OH－=CO32－+CaCO3↓+2H2O 7．A、B、C短周期元素在周期表中的位置如右图所示，已知A、C可分别与B形成化合物X 和Y，A与B的质子数之和等于C的质子数，现有以下说法，判断正确的是A ．B 形成的单质存在同素异形体，C 的单质不存在同素异形体 B ．C 的最高价氧化物对应的水化物能与A 的常见氢化物形成三种盐 C ．常温下，B 的氢化物中无H +D ．Y 的种类比X 多8．下列离子组一定能大量共存的是A ．甲基橙呈黄色的溶液中：I －、Cl －、NO 3－、Na +B ．pH=1的溶液中：Fe 2+、NO 3－、SO 42－、Na +C ．含大量Al 3+的溶液中：K +、Na +、NO 3－、ClO －D ．c (H +)/c (OH －)=1012 的溶液中：NH 4+、Al 3+、Cl －、NO 3－9．500mL 含有0.40 mol 碳酸钠的溶液和某浓度的400 mL 盐酸，不管将前者滴加入后者，还是将后者滴加入前者，都有气体产生，但最终生成的气体体积不同，则盐酸的浓度合理的是 A ．1.2mol/LB ．2 mol/LC ．0.2 mol/LD ．0.4mol/L10．下列各组物质中，气体X 和气体Y 在通常条件下同时通入盛有溶液z 的洗气瓶中(如右图所示)，可能没有沉淀生成的是11．新华网2005年4月2日讯：美国研究人员在网络版《科学》杂志上发表论文说，他们开发出了一种新的固体氧化物燃料电池，在用碳氢化合物――异辛烷做燃料时，能源转换效率有望达到50%。

卜人入州八九几市潮王学校高三理科数学参考答案一、选择题〔本大题一一共12小题，每一小题5分，一共60分〕131174.F+V －E=21(,1]-∞ 三、解答题〔本大题一一共6小题，一共70分〕17、解：〔1〕∵2222cos 4ca b ab C =+-=∴2c =故ABC ∆的周长为5.………………………………………………………………………………6分〔2〕∵1cos 4C =且C 为ABC ∆的内角∴sin C =由正弦定理sin sin a c A C =得sin A =∴7cos 8A = ∴11cos()cos cos sin sin 16A C A C A C -=+=…………………………………………………………………………12分 18、解：(1〕依题知21()2n n n S a a =+……………………………………………………………………………………………………①∴21111()2a a a =+，又0n a >∴11a =21111(a a ),n 22n n n S ---=+≥……………………………………………………………………………………………②由①-②得22111()2n n n n n a a a a a --=-+-∴22111,0nn n n n a a a a a ---+=-->n 且a ,那么11n n a a --=∴{}n a 是等差数列，∴1(1)1n a n n =+-⨯=…………………………………………………………………………6分(2)∵11()()22n n nn b a n ==， ∴2311112()3()222n T n =⨯++⨯+⋅⋅⋅+⨯n1（）2，∴23411111()2()3()2222n T n =⨯++⨯+⋅⋅⋅+⨯n+11（）2，两式相减得123111111()()()-()22222n n T n +=+++⋅⋅⋅+⨯n 1（）2，∴11()112()2(2)()12212nn n n T n n -=-=-+-.…………………………………………………………………………12分19．解：〔1〕证明：在梯形ABCD 中，因为0//,1,60AB CD AD DC CB ABC ===∠=，所以2AB =，所以22202cos 603AC AB BC AB BC =+-=，所以222AB AC BC =+，所以BC AC ⊥．．．．．．．．．．．．．．．．．．．3分因为平面ACFE ⊥平面ABCD ，平面ACFE平面ABCD AC =，因为BC⊂平面ABCD ，所以BC ⊥平面ACFE ．．．．．．．．．．．．5分〔2〕由〔1〕可建立分别以直线,,CA CB CF 为x 轴，y 轴，z 轴的如下列图的空间直角坐标系，令(03FMλλ=≤≤，那么())()()0,0,0,3,0,0,0,1,0,M ,0,1C AB λ，∴()()3,1,0,,1,1AB BM λ=-=-，设()1,,n x y z =为平面MAB 的一个法向量，由1100n AB n BM ⎧=⎪⎨=⎪⎩得300y x y z λ⎧+=⎪⎨-+=⎪⎩，取1x =，那么()11,3,3n λ=-，．．．．．．．．．．．7分∵()21,0,0n =是平面FCB 的一个法向量．．．．．．．．．．．．．．．．．．．．．．．8分∴()()122212cos 133134n n n n θλλ===++-⨯-+．．．．．．．．．．．．．．10分∵03λ≤≤，∴当0λ=时，cos θ7，当3λ=cos θ有最大值12． ∴71cos 2θ⎤∈⎥⎦．．．．．．．．．．．．．．．．．．12分20..解：(1)当l 1与x 轴重合时，k 1＋k 2＝k 3＋k 4＝0，即k 3＝－k 4， ∴l 2垂直于x 轴，得|AB |＝2a ＝2，|CD |＝＝，得a ＝，b ＝，∴椭圆E 的方程为＋＝1. -----------------------------------------------------------4分 (2)焦点F 1，F 2坐标分别为(－1，0)，(1，0)，当直线l 1或者l 2斜率不存在时，P 点坐标为(－1，0)或者(1，0)， ------------------------------------5分 当直线l 1，l 2斜率存在时，设斜率分别为m 1，m 2，设A (x 1，y 1)，B (x 2，y 2)， 由得(2＋3m )x 2＋6mx ＋3m －6＝0，∴x 1＋x 2＝－，x 1x 2＝，k 1＋k 2＝＋＝m 1＝m 1＝m 1＝－， --------------------------------------------------------------------7分同理k 3＋k 4＝－， -----------------------------------------------------------------------------8分 ∵k 1＋k 2＝k 3＋k 4，∴＝，即(m 1m 2＋2)(m 2－m 1)＝0，由题意知m 1≠m 2，∴m 1m 2＋2＝0 -------------------------------------------------------------------9分 设P (x ，y )，那么·＋2＝0，即＋x 2＝1(x ≠±1)， ------------------------------------------------10分又当直线l 1或者l 2斜率不存在时，P 点坐标为(－1，0)或者(1，0)也满足此方程， ∴点P (x ，y )在椭圆＋x 2＝1上，存在点M (0，－1)和点N (0，1)，使得|PM |＋|PN |为定值，定值为2. ---------------------------------12分21、解〔1〕10,(),x f x a x'>=-………………………………………………………………………1分 ()0,()0+f x f x '>∞若a<0,在（，）上单调递增,3)0,0(),ae x f x =->→→-∞3且f(e 时，此时，f(x)存在唯一零点；………………3分10,x a'==1-ax 若a>0,f (x)=x -4当-lna-4>0,即0<a<e 时，f(x)有两个零点。

桐庐分水高级中学2013届高三上第二次阶段性质检数学理试题时间：120分钟 分值：150分一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{}023>+=x x A ，{}0)3)(1(>-+=x x x B ，则=B A I （ ）A ．)1,(--∞B ．⎭⎬⎫⎩⎨⎧--32,1C ．)3,32(-D ．),3(+∞ 2．“4m =-”是“直线820mx y +-=与直线210x my +-=平行”的（ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ． 既不充分又非必要条件3．若110,a b <<则下列不等式:①a b ab +<;②a b >;③a b <;④2b a a b +>中正确的是（ ）A ．①②B ．②③C ．①④D ．③④ 4．已知等差数列}a {n 的公差为2，若431a ,a ,a 成等比数列，则1a =（ ） A ．－4B ．－8C ．－6D ．－105．若圆03222=+-+by ax y x 的圆心位于第三象限，则直线0=++b ay x 一定不经过第（ ）象限A ．四B ．三C ．二D ．一6．若||1,||2,a b c a b ===+r r r r r，且c a ⊥r r ，则向量a r 与b r 的夹角为 ( )A ．30°B ．60°C ．120°D ．150° 7．函数82sin )(3-++=xax x x f )(R a ∈在区间],[n m 上有最大值10，则函数)(x f 在区间],[m n --上有( )A. 最大值-10B. 最小值-10C. 最小值—26D. 最大值-26 8．等比数列{}n a 的各项均为正数，且564718a a a a +=，则3132310log log log a a a ++=L （ ） A ．12B ．10C ．8D ．32log 5+9．函数21()3cos log 22f x x x π=--的零点个数为（ ） A.2B.3C.4D.510．已知函数)0()(23≠+++=a d cx bxax x f 的对称中心为00(,)M x y ，记函数)(x f 的导函数为)(/x f ，)(/x f 的导函数为)(//x f ，则有0)(0//=x f.若函数()323f x x x =-，则可求得1220122012f f ⎛⎫⎛⎫++⎪ ⎪⎝⎭⎝⎭4022...2012f ⎛⎫+ ⎪⎝⎭40232012f ⎛⎫+= ⎪⎝⎭（ ） A ．4023 B ．4023- C ．8046 D ．8046-二、填空题：本大题共7小题，每小题4分，共28分。