下载文档原格式
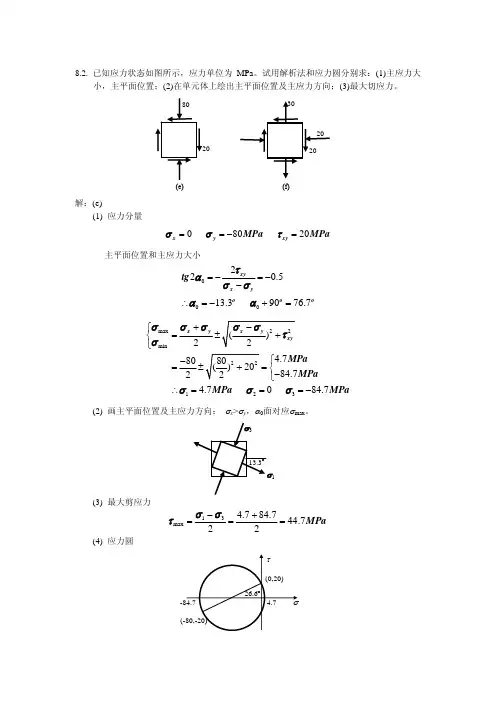
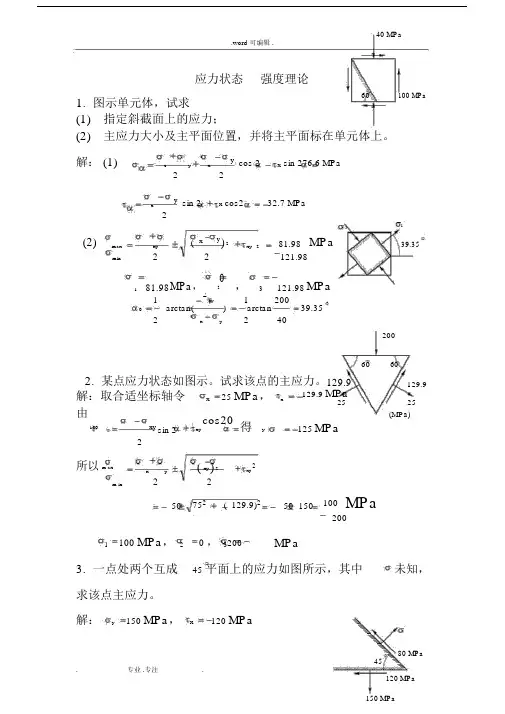
40 MPa.word 可编辑 .应力状态强度理论1. 图示单元体，试求60100 MPa(1)指定斜截面上的应力；(2)主应力大小及主平面位置，并将主平面标在单元体上。
解： (1)x y xy cos 2x sin 276.6 MPa22xy sin 2x cos232.7 MPa231 (2)max xy( x y) 2xy281.98MPa39.35min22121.98181.98MPa，2，3121.98MPa12xy12000arctan()arctan39.352x y24020060602. 某点应力状态如图示。
试求该点的主应力。
129.9129.9解：取合适坐标轴令x25 MPa，x由120xy sin 2xy cos20 得y2所以m axx y( xy ) 2xy 2m in 22129.9 MPa2525(MPa)125MPa50752( 129.9)250 150100 MPa2001 100MPa，20 ，3200MPa3. 一点处两个互成45 平面上的应力如图所示，其中未知，求该点主应力。
解：y150 MPa，x120 MPa.word 可编辑 .由得45xy sin 2xy cos 2x 15080 22x10MPa所以max xy(x y)2222xy min yx454545214.22 MPa 74.221214.22 MPa，20 ，45374.22MPa4.图示封闭薄壁圆筒，内径 d 100 mm，壁厚 t 2 mm，承受内压 p 4 MPa，外力偶矩 M e 0.192 kN·m。
求靠圆筒内壁任一点处的主应力。
0.19210 3解：xπ(0.10440.14)0.05 5.75MPat32x y pd MPa504tpd MPa1002tM e p M emax x y(x y ) 2xy2min22100.7 MPa 49.351100.7MPa，249.35 MPa，3 4 MPa5.受力体某点平面上的应力如图示，求其主应力大小。
22-６ 图示受力板件，试证明A 点处各截面的正应力、剪应力均为零证明：若在尖点A 处沿自由边界取三角形单元体如图所示，设单元体 、面上的应力分量为、和、，自由边界上的应力分量为，则有由于、，因此，必有、、。
这时，代表A 点应力状态的应力圆缩为 坐标的原点，所以A 点为零应力状态。
22-7 图示槽形刚体，在槽内放置一边长为10mm 、的立方钢块，钢块顶面受到合力为P=8kN 的均布压力作用，试求钢块的三个主应力和最大剪应力。
已知材料的弹性模量GPa E 200=，泊松比3.0=μ。
解： 选取坐标轴x 、y 、z 如图。
x σ＝0， σz ＝－10101083⨯⨯＝－80MPa ，εy ＝1E 〔σy －μ（σz ＋σx ）〕＝1E〔σy －μσz 〕＝0 由此得 σy ＝μσz ＝0.3×（－80）=－24 MPa 。
Ｐxzyo将x σ、y σ、z σ按代数值大小排列，得三个主应力为 σ1＝0 、σ2 ＝－24 MPa 、σ3=－80 MPa 。
最大剪应力 τm a x =σσ132-＝280＝40 MPa 。
22-12 试比较图示正方形棱柱体在下列两种情况下的相当应力3xd σ：(a )棱柱体自由受压：(b )棱柱体在刚性方模内受压。
弹性常数E 、μ均为已知.解：对于图（a ）中的情况，应力状态如图（c ）对于图（b ）中的情况，应力状态如图（d ）所以，，22-20 N O.28a普通热轧工字钢简支梁如图所示。
今由贴在中性层上某点K处、与轴线夹45º角方向上的应变片测得ε45º=-260×10-6。
已知钢材的E=210GPa，μ=0.28。
求作用在梁上的载荷F P。
材料⼒学习题第六章应⼒状态分析答案详解第6章应⼒状态分析⼀、选择题1、对于图⽰各点应⼒状态，属于单向应⼒状态的是（A ）。
20（MPa ）20d20（A ）a 点；（B ）b 点；（C ）c 点；（D ）d 点。
2、在平⾯应⼒状态下，对于任意两斜截⾯上的正应⼒αβσσ=成⽴的充分必要条件，有下列四种答案，正确答案是（ B ）。
（A ）,0x y xy σστ=≠；（B ）,0x y xy σστ==；（C ）,0x y xy σστ≠=；（D ）x y xy σστ==。
3、已知单元体AB 、BC ⾯上只作⽤有切应⼒τ，现关于AC ⾯上应⼒有下列四种答案，正确答案是（ C ）。
（A ）AC AC /2,0ττσ==；（B ）AC AC /2,/2ττσ==；（C ）AC AC /2,/2ττσ==；（D ）AC AC /2,/2ττσ=-=。
4、矩形截⾯简⽀梁受⼒如图（a ）所⽰，横截⾯上各点的应⼒状态如图（b ）所⽰。
关于它们的正确性，现有四种答案，正确答案是（ D ）。
(b)(a)（A）点1、2的应⼒状态是正确的；（B）点2、3的应⼒状态是正确的；（C）点3、4的应⼒状态是正确的；（D）点1、5的应⼒状态是正确的。
5、对于图⽰三种应⼒状态（a）、（b）、（c）之间的关系，有下列四种答案，正确答案是（ D ）。
τ(a) (b)(c)（A）三种应⼒状态均相同；（B）三种应⼒状态均不同；（C）（b）和（c）相同；（D）（a）和（c）相同；6、关于图⽰主应⼒单元体的最⼤切应⼒作⽤⾯有下列四种答案，正确答案是（ B ）。
(A) (B) (D)(C)解答：maxτ发⽣在1σ成45o的斜截⾯上7、⼴义胡克定律适⽤范围，有下列四种答案，正确答案是（ C ）。
（A）脆性材料；（B）塑性材料；（C）材料为各向同性，且处于线弹性范围内；（D）任何材料；8、三个弹性常数之间的关系：/[2(1)]G E v =+ 适⽤于（ C ）。
应力状态分析与强度理论
基 本 概 念 题
一、选择题
1. 三种应力状态分别如图(a )、(b )、(c )所示，则三者间的关系为（ ）。
A ．完全等价
B ．完全不等价
C ．图(b )、图(c )等价
D ．图(a )、图(c )等价
题1图
2. 已知应力情况如图所示，则图示斜截面上的应力为（ ）。
（应力单位为 MPa)。
A ．70-=ασ，30-=ατ
B ．0=ασ，30=ατ
C ．70-=ασ，30=ατ
D ．0=ασ，30-=ατ
3. 在纯剪切应力状态中，其余任意两相互垂直截面上的 正应力，必定是（ ）。
A ．均为正值
B ．一为正值一为负值
C ．均为负值 题2图
D ．均为零值
4. 单元体的应力状态如图所示，由x 轴至1σ方向的夹角为（ ）。
A ．︒
5.13 B ．︒-5.76 C ．︒5.76 D ．︒-5.13
题4图 题5图
5. 单元体的应力状态如图所示，则主应力1σ、2σ分别为（ ）。
(应力单位MPa). -33-
A ．901=σ，102-=σ
B ．1001=σ，102-=σ
C ．901=σ，02=σ
D ．1001=σ，02=σ 6. 如图6所示单元体最大剪应力m ax τ为（ ）。
A ．100 MPa
B ．50 MPa
C ．25 MPa
D ．0
题6图 题7图
7. 单元体如图所示，关于其主应力有下列四种答案，正确的是（ ）。
A ．1σ＞2σ，03=σ B ．3σ＜2σ＜0，03=σ01=σ C ．1σ＞0，2σ= 0，3σ＜0，1σ＜3σ D ．1σ＞0，2σ= 0，3σ＜0，1σ＞3σ
8. 已知应力圆如图7-22所示，图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力，则与应力圆所对应的单元体为( )。
A ．图(a )
B ．图(b )
C ．图(c )
D ．图(d )
题8图
9. 在图示四种应力状态中，其应力圆具有相同的圆心和相同的半径是（ ）。
-34-
题9图
A ．图(a )、图(d )
B ．图(b )、图(c )
C ．图(a )、图(b )、图(c ) 、图(d )
D ．图(a )、图(d )、图(b )、图(c )
10. 如图所示，较大体积的钢块上开有一贯穿的槽，槽内嵌入一铝质立方体，铝块受到均布压力P 作用，假设钢块不变形，铝块处于（ ）。
A ．单向应力、单向应变状态
B ．单向应力、二向应变状态
C ．二向应力、二向应变状态
D ．三向应力、三向应变状态
题10图 题11图
11. 平面应力状态如图所示，设︒=45α，材料沿n 方向的正应力ασ和线应变αε为（ ）。
A ．τσ
σα+=2
，E ⎪⎭
⎫
⎝⎛+=τσ
εα2 B ．τσσα-=2，E ⎪⎭⎫ ⎝⎛-=τσεα2
C ．τσ
σα+=2
，()()E E τμσμεα++-=121 D ．τσ
σα-=
2
，()()E E τμσμεα+--=121
12. 广义虎克定律的适用范围是( )
A ．脆性材料
B ．塑性材料
C ．任何材料
D ．材料为各向同性，且处于线弹性范围内
13. 在图所列单元体中，必须采用强度理论进行强度计算的是（ ）。
题13图
14. 铸铁试件拉伸时，沿横截面断裂；扭转时沿与轴线成︒45倾角的螺旋面断裂，这与（ ）有关。
-35-
A ．最大剪应力
B ．最大拉应力
C ．最大剪应力和最大拉应力
D ．最大拉应变
15. 塑性材料构件内有四个点处的应力状态分别如图15(a )、(b )、(c )、(d )所示，其中最容易屈服的点是（ ）。
A ．图(a )
B ．图(b )
C ．图(c )
D ．图(d )
题15图
二、判断题(正确的打“√”，错的打“×”)
1. 单元体最大正应力面上的剪应力恒等于零。
（ ）
2. 单元体最大剪应力面上的正应力恒等于零。
（ ）
3. 正应力最大的面与剪应力最大的面相交成︒45角。
（ ）
4. 正应力最大的面与正应力最小的面必互相垂直。
( )
5. 纯剪应力状态中最大剪应力与最大正应力的值相等。
( )
6. 等截面杆受轴向拉伸，如图所示，A 、B 两点应力状态不相同。
( )
题6图 题7图
7. 某点处应力状态如图所示，材料为各向同性，弹性系数E 、μ已知，线应变x ε、y
ε已知，则)(y x z εεμε+-=。
( )
8. 若受力杆件一点处，沿某方向线应变为零，则该方向的正应力必为零。
( )
9. 应力圆半径是
2
y
x σσ-。
( )
10. 若各向同性材料单元体的三个正应力x σ＞y σ＞z σ，则对应的三个线应变也有x ε＞y ε＞z ε。
( )
-36-
11. 对受力构件进行强度计算时，都需要考虑强度理论。
( )
三、填空题
1. 画出图示各受力构件上指定点处的单元体。
题1图
2. 图示两个单元体的应力状态分别是（ ）和（ ）应力状态(应力单位：MPa)。
题2图
3. 若单元体处于平面应力状态，当x σ、y σ、xy τ三者满足条件x σ=y σ=xy τ＞0时，则该单元体处于（ ）应力状态；当x σ、y σ、xy τ三者满足条件x σ=y σ=xy τ＜0时，则该单元体为（ ）应力状态。
4. 图示梁的A 、B 、C 、D 、E 五点中，，单向应力状态的点是( )，纯剪切应力状态的点是（ ），在任何截面上应力均为零的点是( )。
题4图 题5图
5. 图示应力状态的主应力1σ、2σ、3σ和最大剪应力m ax τ，的值分别为(单为MPa) -37-
图(a )：1σ=（ ），2σ=（ ），3σ=（ ）， m ax τ=（ ）； 图(b )：1σ=（ ），2σ=（ ），3σ=（ ）， m ax τ=（ ）。
6. 图示应力圆各表示什么应力状态? 画出与之相应的单元体及其各面上的应力。
题6图
7. 火车轮轮缘与钢轨接触点处的主应力为 –800 MPa 、–900 MPa 和–1100 MPa ， 按第三和第四强度理论，相当应力分别为（ ）MPa 。
8. 强度理论的任务是（ ）。
9. 四种应力状态如图所示，按第三强度理论，其相当应力最大的是（
），最小的是（ ）。
题9图
计 算 题
1. 构件受力如图所示。
(1)确定危险点的位置。
(2)用单元体表示危险点的应力状态。
题1图
2. 在图示各单元体中，试用解析法和图解法求斜截面ab 上的应力。
应力的单位为MPa 。
-38-
题2图
3. 已知应力状态如图所示，图中应力单位皆为MPa。
试用解析法及图解法求：
(1)主应力大小，主平面位置；
(2)在单元体上绘出主平面位置及主应力方向；
(3)最大切应力。
题3图
4. 二向应力状态如图所示，应力单位为MPa。
试求主并作应力圆。
题4图题5图
5. 在处于二向应力状态的物体的边界bc上，A点处的最大切应力为35 MPa。
试求A 点的主应力。
若在A点周围以垂直于x轴和y
轴的平面分割出单元体，试求单元体各面上的应
力分量。
6. 在通过一点的两个平面上，应力如图所
示，单位为MPa。
试求主应力的数值及主平面
的位置，并用单元体的草图表示出来。
题6图
7. 试求图示各应力状态的主应力及最大切应力（应力单位为MPa）。
-39-
题7图
-40-。
