中考数学专题训练---反比例函数的综合题分类含详细答案

中考数学总复习《反比例函数与一次函数综合》专题训练-附含答案学校:___________班级：___________姓名：___________考号：___________ 1．如图，在平面直角坐标系xOy 中，一次函数1y ax b （a ，b 为常数，且0a ≠）与反比例函数2m y x=（m 为常数，且0m ≠）的图象交于点()2,1A -和()1,B n ．(1)求反比例函数与一次函数的解析式．(2)连接OA 、OB ，求△AOB 的面积．(3)直接写出当12y y <时，自变量x 的取值范围．2．定义：在平面直角坐标系中，如果一个点的纵坐标等于它的横坐标的三倍，则称该点为“纵三倍点”．例如()()()1,3,2,6,2,32--都是“纵三倍点”． (1)下列函数图象上只有一个“纵三倍点”的是______；（填序号）△21y x =-+；△21y x=；△21y x x =++． (2)已知抛物线2y x mx n =++（,m n 均为常数）与直线4y x =+只有一个交点，且该交点是“纵三倍点”，求抛物线的解析式；(3)若抛物线232y ax bx （,a b 是常数，0a >）的图象上有且只有一个“纵三倍点”，令226w b b a =-+，是否存在一个常数t ，使得当1t b t ≤≤+时，w 的最小值恰好等于t ，若存在，求出t 的值；若不存在，请说明理由．3．如图，点A 在反比例函数()0k y x x=>的图象上，AB y ⊥轴于点B ，且24OB AB ==．(1)求反比例函数的解析式； (2)点C 在这个反比例函数图象上，连接AC 并延长交x 轴于点D ，且45ADO ∠=︒，求点C 的坐标． 4．如图，在平面直角坐标系中，一次函数3yx 的图象与反比例函数(0)k y x x=>的图象交于点(,4)A a ，求此反比例函数的表达式．5．如图，一次函数()10y mx n m =+≠的图象与反比例函数()20k y k x=≠的图象交于(),1A a -，()1,3B -两点，且一次函数的图象交x 轴于点C ，交y 轴于点D ．(1)求一次函数和反比例函数的解析式；(2)在第四象限的反比例图象上有一点P ，使得4=△△OCP OBD S S ，请求出点P 的坐标；(3)对于反比例函数()20k y k x=≠，当3y ≤时，直接写出x 的取值范围． 6．如图，已知反比例函数11k y x =的图象与直线22y k x b =+相交于()1,3A -，(3,)B n 两点．(1)求反比例函数与一次函数的解析式； (2)求△AOB 的面积；(3)直接写出当12y y >时，对应的x 的取值范围．7．如图，在平面直角坐标系中，一次函数1y k x b =+（10k ≠）的图象与反比例函数2k y x=（20k ≠）的图象相交于()3,4A ，()4,B m -两点．(1)求一次函数和反比例函数的解析式，并直接写出一次函数的值大于反比例函数的值时x 的取值范围；(2)若点D 在x 轴上，位于原点右侧，且OA OD =，求:ABO ABD S S △△．8．如图，一次函数5y x =-+的图象与函数(0,0)n y n x x=>>的图象交于点(4,)A a 和点B ．(1)求n 的值；(2)若0x >，根据图象直接写出当5n x x-+>时x 的取值范围； (3)点P 在线段AB 上，过点P 作x 轴的垂线，交函数n y x =的图象于点Q ，若POQ △的面积为1，求点P 的坐标．9．如图，一次函数()110y k x b k =+≠与反比例函数()220k y k x=≠的图象交于点()2,3A 和(),1B a -，设直线AB 交x 轴于点C ．(1)求反比例函数和一次函数的表达式；(2)若点P 是反比例函数图象上的一点，且POC △是以OC 为底边的等腰三角形，求P 点的坐标． 10．如图，在平面直角坐标系xOy 中，一次函数1152y x =+和22y x =-的图象相交于点A ，反比例函数3k y x =的图象经过点A ．(1)则反比例函数的表达式为________；(2)当13y y <时，x 的取值范围为________．(3)求AOB 的面积．11．如图，已知反比例函数k y x=的图象与一次函数y mx =图象的一个交点为()4,,A m AB x ⊥轴，且AOB 的面积为4．(1)求k 和m 的值；(2)若两函数图象的另一交点为C ，直接写出点C 的坐标__________．12．已知 ()()4428A B --，，，是一次函数y kx b =+的图象和反比例函数m y x=的图象的两个交点，直线AB 与y 轴交于点C ．(1)求反比例函数和一次函数的关系式；(2)求AOC 的面积；(3)结合图象直接写出不等式m kx b x +>的解集． 13．如图，直线32y x =与双曲线(0)k y k x=≠交于A ，B 两点，点A 的坐标为(,3)m -，点C 是双曲线第一象限分支上的一点，连结BC 并延长交x 轴于点D ，且2BC CD =．(1)求k 的值，并直接写出点B 的坐标；(2)点G 是y 轴上的动点，连结GB ，GC ，求GB GC +的最小值和点G 坐标；(3)P 是坐标轴上的点，Q 是平面内一点，是否存在点P ，Q ，使得四边形ABPQ 是矩形？若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．14．如图，直线3y x b =+与x 轴交于点()1,0A -，与反比例函数()0ky x x=>的图象相交于点()1,B m ．(1)求反比例函数的表达式；(2)C 是反比例函数()0k y x x=＞的图象上的一点，连接AC ，若45CAO ∠=︒，求直线BC 的函数表达式． 15．如图，一次函数1=y ax b +的图象过点()40A -，，与y 轴交于点B ，与反比例函数(2>0)k y x x =的图象交于点C ．D 为AB 的中点，过点D 作x 轴的平行线，交反比例函数的图象于点E ，连接OE ．(1)当=3OB ，=6DE 时，求k 的值；(2)若635OB OE ==，，求一次函数的解析式和点C 的坐标．参考答案： 1．(1)2y x=- =1y x -- (2)1.5(3)20x -<<或1x >2．(1)△△(2)238y x x =-+(3)1t =3．(1)8y x= (2)()4,2C4．反比例函数的表达式为4y x =． 5．(1)一次函数的解析式为12y x =-+；(2)点P 的坐标为3,44⎛⎫- ⎪⎝⎭(3)1x ≤-或0x >6．(1)13y x=- 22y x =-+； (2)4；(3)10x -<<或3x >．7．(1)一次函数的关系式为1y x =+；40x -<<或3x >(2)1:68．(1)4(2)14x <<(3)(2,3)P 或(3,2)9．(1)6y x = 122y x =+(2)()2,3P --10．(1)38y x =-(2)8x <-或20x -<<(3)1511．(1)18,2k m ==(2)()4,2--12．(1)16y x = 24y x =+(2)8(3)40x -<<或2x >13．(1)623k B =，，(2)217(3)存在，点P 的坐标为1302⎛⎫ ⎪⎝⎭， 或1303⎛⎫⎪⎝⎭，14．(1)反比例函数的表达式为6y x =；(2)直线BC 的函数表达式为39y x =-+．15．(1)6k =(2)162y x =+，点C 的坐标为()29，。

反比例函数1．正比例函数y ＝6x 的图象与反比例函数y ＝6x的图象的交点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第一、三象限[解析] D ∵正比例函数y ＝6x 与反比例函数y ＝6x 中比例系数k ＝6＞0，∴两函数的图象都经过第一、三象限，∴两函数图象的交点有两个，分别位于第一、三象限，故选择D .2． 若ab ＜0，则正比例函数y ＝ax 和反比例函数y ＝bx在同一坐标系中的大致图象可能是( )图1－ZT －1[解析] C (1)当a>0，b<0时，可知正比例函数y ＝ax 的图象经过第一、三象限，反比例函数y ＝bx 的图象在第二、四象限；(2)当a<0，b>0时，可知正比例函数y ＝ax 的图象经过第二、四象限，反比例函数y ＝bx的图象在第一、三象限．通过比较可得正确选项是C .3．[鄂州中考] 已知正比例函数y ＝－4x 与反比例函数y ＝kx 的图象交于A ，B 两点，若点A 的坐标为(x ，4)，则点B 的坐标为________．[答案] (1，－4)[解析] 把y ＝4代入y ＝－4x ，得x ＝－1，∴A(－1，4)．∵正比例函数与反比例函数的图象在不同象限的交点关于原点成中心对称，∴点B 的坐标为(1，－4)．类型之二 反比例函数与一次函数的综合应用4．[陕西中考] 如果一个正比例函数的图象与一个反比例函数y ＝6x 的图象交于A(x 1，y 1)，B(x 2，y 2)两点，那么(x 2－x 1)(y 2－y 1)的值为________．[答案] 24[解析] ∵点A ，B 在反比例函数y ＝6x 的图象上，∴x 1y 1＝6.∵正比例函数与反比例函数的图象在不同象限的交点关于原点成中心对称，∴x 2＝－x 1，y 2＝－y 1，∴(x 2－x 1)(y 2－y 1)＝(－x 1－x 1)(－y 1－y 1)＝4x 1y 1＝4×6＝24.5．[郴州中考] 已知直线l 平行于直线y ＝2x ＋1，并与反比例函数y ＝1x 的图象交于点A(a ，1)．求直线l 的函数表达式．解：∵反比例函数y ＝1x 的图象过点A(a ，1)，∴1＝1a ，∴a ＝1，∴点A 的坐标为(1，1)． ∵直线l 平行于直线y ＝2x ＋1，∴可设直线l 的函数表达式为y ＝2x ＋b ，把点A(1，1)的坐标代入，得 1＝2×1＋b ，∴b ＝－1，∴直线l 的函数表达式为y ＝2x －1.6．如图1－ZT －2，在平面直角坐标系xOy 中，一次函数y ＝ax ＋b 的图象与x 轴交于点A(－2，0)，与y 轴交于点C ，与反比例函数y ＝kx 在第一象限的图象交于点B(m ，n)，连接OB ，若S △AOB ＝6，S △BOC ＝2.(1)求一次函数的表达式； (2)求反比例函数的表达式．图1－ZT －2解：过点B 分别作x 轴、y 轴的垂线，垂足分别为E ，D. 因为S △AOB ＝6，S △BOC ＝2， 所以S △AOC ＝4.又点A(－2，0)，所以OA ＝2， 所以OC ＝4.又S △BOC ＝2，所以BD ＝1， 因为AO ＝2，S △AOB ＝6，所以BE ＝6，所以点B 的坐标为(1，6)．(1)因为一次函数y ＝ax ＋b 的图象过点A ，B ，所以⎩⎪⎨⎪⎧－2a ＋b ＝0，a ＋b ＝6，解得⎩⎪⎨⎪⎧a ＝2，b ＝4，即一次函数的表达式为y ＝2x ＋4.(2)因为反比例函数y ＝kx 的图象过点B ，所以6＝k1，即k ＝6，所以反比例函数的表达式为y ＝6x.7．如图1－ZT －3所示，直线y ＝k 1x ＋b 与双曲线y ＝k 2x 相交于A(1，2)，B(m ，－1)两点．(1)求直线和双曲线的函数表达式；(2)若A 1(x 1，y 1)，A 2(x 2，y 2)，A 3(x 3，y 3)为双曲线上的三点，且x 1＜x 2＜0＜x 3，请直接写出y 1，y 2，y 3的大小关系；(3)观察图象，请直接写出不等式k 1x ＋b ＞k 2x的解集．图1－ZT －3解：(1)∵双曲线y ＝k 2x 经过点A(1，2)，∴k 2＝2，∴双曲线的函数表达式为y ＝2x .∵点B(m ，－1)在双曲线y ＝2x 上，∴m ＝－2，则B(－2，－1)．由A(1，2)，B(－2，－1)两点在直线y ＝k 1x ＋b 上，得⎩⎪⎨⎪⎧k 1＋b ＝2，－2k 1＋b ＝－1，解得⎩⎪⎨⎪⎧k 1＝1，b ＝1，∴直线的函数表达式为y ＝x ＋1. (2)y 2<y 1<y 3. (3)x>1或－2<x<0.类型之三 反比例函数与几何图形的综合应用8．如图1－ZT －4，在平面直角坐标系中，反比例函数y ＝kx (x>0)的图象和矩形ABCD 在第一象限，AD 平行于x 轴，且AB ＝2，AD ＝4，点A 的坐标为(2，6)．(1)直接写出B ，C ，D 三点的坐标；(2)若将矩形向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求矩形的平移距离和反比例函数的表达式．图1－ZT －4解：(1)B(2，4)，C(6，4)，D(6，6)．(2)点A ，C 同时落在反比例函数的图象上．如图1－ZT －5，矩形ABCD 平移后得到矩形A ′B ′C ′D ′.图1－ZT －5设平移距离为a ，则A′(2，6－a)，C ′(6，4－a)． ∵点A′，C ′在函数y ＝kx 的图象上，∴2(6－a)＝6(4－a)，解得a ＝3，∴点A′(2，3)，∴矩形的平移距离为3，反比例函数的表达式为y ＝6x.9．如图1－ZT －6，已知反比例函数y ＝k 13x 的图象与一次函数y ＝k 2x ＋m 的图象交于A(－1，a)，B(13，－3)两点，连接AO. (1)求反比例函数和一次函数的表达式；(2)设点C 在y 轴上，且与点A ，O 构成等腰三角形，请直接写出点C 的坐标．图1－ZT －6解：(1)∵反比例函数y ＝k 13x 的图象经过点B(13，－3)，∴k 1＝3×13×(－3)＝－3.∵反比例函数y ＝k 13x 的图象经过点A(－1，a)，∴a ＝1.由直线y 2＝k 2x ＋m 过点A ，B ，得 ⎩⎪⎨⎪⎧－k 2＋m ＝1，13k 2＋m ＝－3，解得⎩⎪⎨⎪⎧k 2＝－3，m ＝－2， ∴反比例函数的表达式为y ＝－1x，一次函数的表达式为y ＝－3x －2.(2)点C 在y 轴上，且与点A ，O 构成等腰三角形，则点C 的坐标为(0，－2)或(0，2)或(0，2)或(0，1)．10．如图1－ZT －7，一次函数y ＝kx ＋b 的图象与反比例函数y ＝mx (x ＞0)的图象交于点P(n ，2)，与x 轴交于点A(－4，0)，与y 轴交于点C ，PB ⊥x 轴于点B ，且AC ＝BC.(1)求一次函数、反比例函数的表达式．(2)反比例函数图象上是否存在一点D ，使四边形BCPD 为菱形，如果存在，求出点D 的坐标；如果不存在，请说明理由．图1－ZT －7解：(1)∵AC＝BC ，CO ⊥AB ，∴AO ＝BO. ∵A(－4，0)，∴B(4，0)，∴P(4，2)． 把P(4，2)的坐标代入y ＝mx ，得m ＝8，∴反比例函数的表达式为y ＝8x.把A(－4，0)，P(4，2)的坐标代入y ＝kx ＋b ，得⎩⎪⎨⎪⎧0＝－4k ＋b ，2＝4k ＋b ，解得⎩⎪⎨⎪⎧k ＝14，b ＝1.∴一次函数的表达式为y ＝14x ＋1.(2)存在点D ，使四边形BCPD 为菱形． ∵AC ＝BC ，∴∠CAB ＝∠ABC. ∵PB ⊥x 轴，∴∠APB ＋∠CAB＝90°，∠PBC ＋∠ABC＝90°， ∴∠APB ＝∠PBC，∴CP ＝CB.由y ＝14x ＋1，知当x ＝0时，y ＝1，如图1－ZT －8过点C 作CD 平行于x 轴，交PB 于点E ，交反比例函数y ＝8x的图象于点D ，连接PD ，BD.图1－ZT －8∴点D 的坐标为(8，1)，BP ⊥CD ， ∴PE ＝BE ＝1，∴CE ＝DE ＝4， ∴PB 与CD 互相垂直平分， ∴四边形BCPD 为菱形， ∴点D(8，1)即为所求．。

中考数学《反比例函数》专项复习综合练习题-附含答案一、单选题1．已知反比例函数y=- 12x,则（）A．y随x的增大而增大B．当x>-3且x≠0时，y>4C．图象位于一、三象限D．当y<-3时，0<x<42．甲、乙、丙三位同学分别正确指出了某一个函数的一个性质．甲：函数图象经过第一象限；乙：函数图象经过第三象限；丙：每第一个象限内 y值随x值的增大而减小．根据他们的描述这个函数表达式可能是（）A．y=2x B．y= 2x C．y=﹣1xD．y=2x23．反比例函数y=kx(k>0)在第一象限内的图象如图，点M是图象上一点 MP垂直x轴于点P 如果△MOP 的面积为1 那么k的值是( )A．1 B．2 C．4 D．√24．如图，反比例函数y=kx(x<0)交边长为10的等边△ OAB的两边于C、D两点，OC＝3BD，则k的值（）A．−9√3B．9√3C．－10√3D．10√35．抛物线y=ax2+bx+c图象如图所示，则一次函数y=﹣bx﹣4ac+b2与反比例函数y= a+b+cx在同一坐标系内的图象大致为（）A．B．C．D．√3 6．如图，点D是▱OABC内一点，AD与x轴平行，BD与y轴平行，BD=√3∠BDC=120°S△BCD=92 (x<0)的图象经过C、D两点，则k的值是（）若反比例函数y=kxA．−6√3B．-6 C．−12√3D．-127．如图，已知在平面直角坐标系xOy中，O是坐标原点，点A是函数y=1（x＜0）图象上一点，AO的延长x（x＞0 k是不等于0的常数）的图象于点C，点A关于y轴的对称点为A′，点C关于x 线交函数y=k2x轴的对称点为C′，交于x轴于点B 连结AB AA′、 A′C′．若△ABC的面积等于6，则由线段AC CC′C′A′ A′A所围成的图形的面积等于（）A．8 B．10 C．3√10D．4√68．如图，反比例函数y=kx与一次函数y=kx﹣k+2在同一直角坐标系中的图象相交于A B两点其中A（﹣1 3）直线y=kx﹣k+2与坐标轴分别交于C D两点下列说法：①k＜0；②点B的坐标为（3 ﹣1）；③当x＜﹣1时kx ＜kx﹣k+2；④tan∠OCD=﹣1k其中正确的是（）A．①③B．①②④C．①③④D．①②③④二、填空题9．已知反比例函数y=﹣2x若y≤1，则自变量x的取值范围是．10．在平面直角坐标系中若一条平行于x轴的直线l分别交双曲线y=﹣6x 和y= 2x于A B两点 P是x轴上的任意一点，则△ABP的面积等于11．如图，在平面直角坐标系中正方形ABCD的面积为20 顶点A在y轴上顶点C在x轴上顶点D在双曲线y=kx(x>0)的图象上边CD交y轴于点E 若CE=ED，则k的值为.12．如图，点 P 是反比例函数图象上的一点 过点 P 向 x 轴作垂线 垂足为 M 连结 PO 若阴影部分面积为 6 ，则这个反比例函数的关系式是 ．13．如图，已知A （ 12 y 1） B （2 y 2）为反比例函数y ＝ 1x 图象上的两点 动点P （x 0）在x 轴正半轴上运动 当线段AP 与线段BP 之差达到最大时 点P 的坐标是 .三、解答题14．如图，反比例函数y =kx (x >0)的图像分别交正方形OABC 的边AB 、BC 于点D 、E 若A 点坐标为(1，0) 若△ODE 是等边三角形 求k 的值.15．某水果生产基地在气温较低时 用装有恒温系统的大棚栽培一种新品种水果 如图是试验阶段的某天恒温系统从开启到关闭后 大棚内的温度y(℃)与时间x(ℎ)之间的函数关系 其中线段AB 、BC 表示恒温系统开启后阶段 双曲线的一部分CD 表示恒温系统关闭阶段．．．．．．．．．．． 请根据图中信息解答下列问题：（1）这个恒温系统设定的恒定温度为多少℃；（2）求全天的温度y(℃)与时间x(ℎ)之间的函数表达式；（3）若大棚内的温度低于10℃时 蔬菜会受到伤害．问：这天内恒温系统最多可以关闭多少小时 才能避免水果生长受到影响？16．如图，已知点A在反比函数y=kx(k<0)的图象上点B在直线y=x−3的图象上点B的纵坐标为－1 AB⊥x轴且S△OAB=4．（1）求点A的坐标和k的值；（2）若点P在反比例函数y=kx(k<0)的图象上点Q在直线y=x−3的图象上P、Q两点关于y轴对称设点P的坐标为(m，n)求nm +mn的值．17．如图，点A在反比例函数y=kx(x>0)的图象上AB⊥x轴于点B AB的垂直平分线PD交双曲线与点P．（1）若点A的坐标为(1 8)，则点P的坐标为．（2）若AP⊥BP点A的横坐标为m．①求k与m之间的关系式；②连接OA OP若△AOP的面积为6 求k的值．18．如图，一次函数y＝k1x+b与反比例函数y＝k2x的图象交于A（2 m） B（n ﹣2）两点．过点B作BC⊥x轴垂足为C 且S△ABC＝5．（1）求一次函数与反比例函数的解析式；（2）根据所给条件请直接写出不等式k1x+b＞k2x的解集；（3）若P（p y1） Q（﹣2 y2）是函数y＝k2x 图象上的两点且y1≥y2求实数p的取值范围．答案1．D 2．B 3．B 4．A 5．D 6．C 7．B 8．C9．x ≤﹣2或x ＞0 10．4 11．4 12．y =−12x 13．(52, 0)14．解：由题意可得△OAD ≅△OCE 设AD =x ，则：DB =EB =1−x 因为OD 2=x 2+1 且△ODE 是等边三角形所以 x 2+1=(1−x)2+(1−x)2 x 1=2+√3 x 2=2−√3 2+√3>1舍去 所以x =2−√3则K =1∗(2−√3)=2−√315．（1）解：设线段AB 表达式为y =kx +b(k ≠0) ∵线段AB 过点(0，10) (2，14)∴{b =102k +b =14解得{b =10k =2∴线段AB 的表达式为：y =2x +10(0≤x ≤5) 当x =5时 y =2×5+10=20 ∴恒定温度为：20℃； （2）解：由（1）可知：线段AB 的表达式为：y =2x +10(0≤x ≤5) B 坐标为(5，20) ∴根据图象可知线段BC 的表达式为：y =20(5<x ≤10)设双曲线CD 解析式为：y =m x(m ≠0)∵C(10，20)∴可得：m10=20 解得：m =200∴双曲线CD 的解析式为：y =200x(10<x ≤24)∴y 关于x 的函数表达式为：y ={2x +10(0≤x ≤5)20(5<x ≤10)200x (10<x ≤24)；（3）解：把y =10代入y =200x中得10=200x解得：x =20∴20−10=10（小时）∴恒温系统最多可以关闭10小时． 16．（1）解：由题意B(2，−1)∵12×2×AB =4 ∴AB =4∵AB//y 轴∴A(2，−5)∵A(2，−5)在y =kx 的图象上 ∴k =−10.（2）解：设P(m ，−10m )，则Q(−m ，−10m ) ∵点Q 在y =x −3上∴−10m=−m −3 整理得：m 2+3m −10=0 解得m =−5或2 当m =−5 n =2时 n m +m n =−2910 当m =2 n =−5时 nm +m n=−2910故n m +m n=−2910.17．（1）（2 4）（2）解：①由题意得 点A 的纵坐标为km 即AB ＝km ∵PD 垂直平分AB ∴PA ＝PB ∵AP ⊥BP∴△PAB 是等腰直角三角形 ∴∠PAB ＝∠PBA ＝45° ∵PD ⊥AB∴△DAP 和△DBP 是等腰直角三角形 ∴DA ＝DB ＝DP ＝k2m ∴P （m +k2m ，k 2m ）将P （m +k2m ，k2m ）代入y =kx 可得：(m +k2m )⋅k2m =k 整理得：k =2m 2；②过点P 作PC ⊥x 轴于点C ，则四边形PABC 是梯形∵S △AOB ＝S △POC ＝k2 ∴S △AOE ＝S 四边形PEBC ∴S △AOP ＝S 梯形PABC ＝6 ∴(k 2m +k m )⋅k2m2=6 整理得：k 2=16m 2∵k =2m 2 ∴k 2=8k解得：k =8或k =0（舍去） ∴k =8．18．（1）把 A(2，m) B(n ，−2) 代入 y =k 2x得： k 2=2m =−2n即m=−n则A(2，−n)过A作AE⊥x轴于E过B作BF⊥y轴于F延长AE、BF交于D ∵A(2，−n)B(n，−2)∴BD=2−n AD=−n+2BC=|−2|=2∵SΔABC=12·BC·BD∴12×2×(2−n)=5解得：n=−3即A(2，3)B(−3，−2)把A(2，3)代入y=k2x得：k2=6即反比例函数的解析式是y=6x；把A(2，3)B(−3，−2)代入y=k1x+b得：{3=2k1+b−2=−3k1+b解得：k1=1b=1即一次函数的解析式是y=x+1；（2）∵A(2，3)B(−3，−2)∴不等式k1x+b>k2x的解集是−3<x<0或x>2；（3）分为两种情况：当点P在第三象限时要使y1⩾y2实数p的取值范围是p⩽−2当点P在第一象限时要使y1⩾y2实数p的取值范围是p>0即P的取值范围是p⩽−2或p>0。

2023年九年级中考数学专题专练--反比例函数与一次函数的综合1．如图，在平面直角坐标系中，点A(m ，n)（m ＞0）在双曲线y ＝ 上.4x （1）如图1，m ＝1，∠AOB ＝45°，点B 正好在y ＝ （x ＞0）上，求B 点坐标； 4x （2）如图2，线段OA 绕O 点旋转至OC ，且C 点正好落在y ＝ 上，C(a ，b)，试求m 与a4x 的数量关系.2．如图，一次函数y=kx+3的图象与反比例函数y= 的图象交于P 、Q 两点，PA ⊥x 轴于点A ，mx 一次函数的图象分别交x 轴、y 轴于点C ，点B，其中OA=6，且 ．12OC CA（1）求一次函数和反比例函数的表达式； （2）求△APQ 的面积；（3）根据图象写出当x 取何值时，一次函数的值小于反比例函数的值．3．如图，已知一次函数y 1=k 1x+b （k 1为常数，且k 1≠0）的图象与反比例函数y 2= （k 2为常数，2k x 且k 2≠0）的图象相交于A （1，2），B （m ，﹣1）两点．（1）求一次函数和反比例函数的解析式；（2）若A 1（m 1，n 1），A （m 2，n 2），A 3（m 3，n 3）为反比例函数图象上的三点，且m 1＜m 2＜0＜m 3，请直接写出n 1、n 2、n 3的大小关系式；（3）结合图象，请直接写出关于x 的不等式k 1x+b ＞ 的解集．2k x 4．如图，在平面直角坐标系xOy 中，直线y=x﹣2与双曲线y= (k≠0)相交于A，B 两点，且点Akx 的横坐标是3.（1）求k 的值；（2）过点P(0，n)作直线，使直线与x 轴平行，直线与直线y=x﹣2交于点M ，与双曲线y=kx (k≠0)交于点N ，若点M 在N 右边，求n 的取值范围.5．已知双曲线y= 和直线y=kx+4．6x （1）若直线y=kx+4与双曲线y= 有唯一公共点，求k 的值．6x（2）若直线y=kx+4与双曲线交于点M （x 1，y 1），N （x 2，y 2）．当x 1＞x 2，请借助图象比较y 1与y 2的大小．6．如图，已知A （﹣2，﹣2），B （1，4）是一次函数y ＝kx+b （k≠0）的图象和反比例函数（m≠0）的图象的两个交点，直线AB 与y 轴交于点C.my x =（1）求一次函数和反比例函数的解析式；（2）求△AOC 的面积；（3）结合图象直接写出不等式的解集.mkx b x +＜7．如图，在平面直角坐标系系中，一次函数y 1=kx+b(k0）与反比例函数y 2= （m≠0）的图象交mx 于第二、第四象限A ，B 两点，过点A 作AD ⊥x 轴，垂足为D ，AD=4，sin ∠AOD= ，且点B 的45坐标为（n ，-2）．（1）求一次函数与反比例函数的表达式；（2）将一次函数y 1=kx+b(k0）向下移动2个单位的函数记为y 3，当y 3<y 2时，求x 的取值范围。

中考数学教材重点--- 反比例函数与一次函数的综合真题练习（含答案解析）1．（2023•攀枝花模拟）如图，已知直线y＝mx与双曲线的一个交点坐标为（﹣1，3），则它们的另一个交点坐标是（）A．（1，3）B．（3，1）C．（1，﹣3）D．（﹣1，3）【分析】反比例函数的图像是中心对称图形，则与经过原点的直线的两个交点一定关于原点对称．【解答】解：因为直线y＝mx过原点，双曲线的两个分支关于原点对称，所以其交点坐标关于原点对称，一个交点坐标为（﹣1，3），另一个交点的坐标为（1，﹣3）．故选：C．2．（2023•滨湖区一模）在平面直角坐标系xOy中，反比例函数与一次函数y ＝ax+b（a＞0）的图像相交于A（﹣8，m）、B（﹣2，n）两点，若△AOB面积为15，则k的值为（）A．﹣8B．﹣7.5C．﹣6D．﹣4【分析】过点A、B分别作y轴的垂线，垂足分别为C、D，根据点A（﹣8，m）、B（﹣2，n）都在反比例函数的图像上，推出n＝4m，根据S梯形ACDB＝S△OAB＝15，求得n﹣m＝3，进一步计算即可求解．【解答】解：∵反比例函数与一次函数y＝ax+b（a＞0）的图像相交于A （﹣8，m）、B（﹣2，n）两点，∴A（﹣8，m）、B（﹣2，n）两点在第二象限，过点A、B分别作y轴的垂线，垂足分别为C、D，则AC＝8，BD＝2，OC＝m，OD＝n，∴CD＝n﹣m，∵点A（﹣8，m）、B（﹣2，n）都在反比例函数的图像上，∴S△AOC＝S△BOD，﹣8m＝﹣2n，即n＝4m，∵S△AOC+S梯形ACDB＝S△BOD+S△OAB，∴S梯形ACDB＝S△OAB＝15，即，∴n﹣m＝3，∴4m﹣m＝3，解得m＝1，∴A（﹣8，1），∴k＝﹣8×1＝﹣8．故选：A．3．（2023•宁波模拟）如图，一次函数y1＝x﹣1的图像与反比例函数的图像交于点A （2，m），B（n，﹣2），当y1＞y2时，x的取值范围是（）A．x＜﹣1或x＞2B．x＜﹣1或0＜x＜2C．﹣1＜x＜0或0＜x＜2D．﹣1＜x＜0或x＞2【分析】先把B（n，﹣2）代入y1＝x﹣1，求出n值，再根据图像直接求解即可．【解答】解：把B（n，﹣2）代入y1＝x﹣1，得﹣2＝n﹣1，解得：n＝﹣1，∴B（﹣1，﹣2），∵图像交于A（2，m）、B（﹣1，﹣2）两点，∴当y1＞y2时，﹣1＜x＜0或x＞2．故选：D．4．（2023•宁德模拟）如图，已知直线l与x，y轴分别交于A，B两点，与反比例函数的图像交于C，D两点，连接OC，OD．若△AOC和△COD的面积都为3，则k的值是（）A．﹣2B．﹣3C．﹣4D．﹣6【分析】由S△AOC＝S△COD得，AC＝CD，设C（，m），A（0，n），由中点坐标公式得，D（，2m﹣n），代入解析式得到n＝m，过点作CH⊥y轴于H，利用S△AOC＝3，可求出k．【解答】解：如图，∵S△AOC＝S△COD，以AC，CD作底，高相同∴AC＝CD，即C为AD的中点，设C（，m），A（0，n），由中点坐标公式得，D（，2m﹣n），∵D（，2m﹣n）在反比例函数y＝的图像上，∴，∴n＝m过点作CH⊥y轴于H，则CH＝﹣，OA＝n＝m，∵S△AOC＝3，∴OA•CH＝3，∴×m×（﹣）＝3，∴k＝﹣4．故选：C．5．（2023•宿迁模拟）如图，在平面直角坐标系中，直线l与函数的图像交于A、B两点，与x轴交于C点，若OA＝AB，且∠OAB＝90°，则tan∠AOC的值为（）A．B．C．D．【分析】作AE⊥x轴于E，BF⊥y轴于F，交于点D，设A（m，），则OE＝m，AE＝，通过证得△AOE≌△BAD（AAS），求得B（），代入，即可得到（m﹣）（m+）＝k，整理得m2﹣＝k，方程两边同除k得﹣＝1，设＝y，则方程变为﹣y＝1，化为y2+y﹣1＝0，解得y＝，即可求得tan∠AOC ＝＝＝＝．【解答】解：作AE⊥x轴于E，BF⊥y轴于F，交于点D，设A（m，），则OE＝m，AE＝，∵∠OAB＝90°，∴∠OAE+∠DAB＝90°，∵∠OAE+∠AOE＝90°，∴∠DAB＝∠AOE，∵OA＝AB，∠AEO＝∠ADB＝90°，∴△AOE≌△BAD（AAS），∴AD＝OE＝m，BD＝AE＝，∴B（），∵函数的图像过B点，∴（m﹣）（m+）＝k，整理得m2﹣＝k，方程两边同除以k得﹣＝1，设＝y，则方程变为﹣y＝1，化为y2+y﹣1＝0，解这个方程得y＝，∴k＞0，∴＞0，∴＝，∴tan∠AOC＝＝＝＝．故选：A．6．（2023•呼和浩特一模）如图，在平面直角坐标系中，直线y＝﹣3x+3交x轴于A点，交y轴于B点，以AB为边在第一象限作正方形ABCD，其中顶点D恰好落在双曲线上，现将正方形ABCD沿y轴向下平移a个单位，可以使得顶点C落在双曲线上，则a的值为（）A．B．C．2D．【分析】作CE⊥y轴于点E，作DF⊥x轴于点F，作CH⊥x轴于点H，交双曲线于点G，由函数解析式确定B的坐标是（0，3），A的坐标是（1，0），根据全等三角形的判定和性质得出△OAB≌△FDA≌△BEC，AF＝OB＝EC＝3，DF＝OA＝BE＝1，结合图形求解即可．【解答】解：作CE⊥y轴于点E，作DF⊥x轴于点F，作CH⊥x轴于点H，交双曲线于点G在y＝﹣3x+3中，令x＝0，解得：y＝3，即B的坐标是（0，3），令y＝0，解得：x＝1，即A的坐标是（1，0），则OB＝3，OA＝1．∵∠BAD＝90°，∴∠BAO+∠DAF＝90°，∵直角△ABO中，∠BAO+∠OBA＝90°，∴∠DAF＝∠OBA，在△OAB和△FDA中，，∴△OAB≌△FDA（AAS），同理，△OAB≌△FDA≌△EBC，∴AF＝OB＝EC＝3，DF＝OA＝BE＝1，故D的坐标是（4，1），C的坐标是（3，4），代入y＝得：k＝4，则函数的解析式是：y＝．∴OE＝4，则C的纵坐标是4，把x＝3代入y＝得：y＝．即G的坐标是，∴CG＝4﹣＝，∴a＝，故选：A．7．（2023•徐州模拟）如图，一次函数的图像与反比例函数的图像交于点A，与y轴交于点C，AD⊥x轴于点D，点D坐标为（4，0），则△ADC的面积为（）A．3B．6C．8D．12【分析】根据AD⊥x轴，D（4，0）求出点A的横坐标，代入一次函数表达式中求出点A纵坐标，再利用三角形面积公式计算．【解答】解：∵AD⊥x轴，D（4，0），∴x A＝4，代入中，∴，即A（4，3），∴△ADC的面积为，故选：B．8．（2023•茅箭区一模）如图已知反比例函数C1：的图像如图所示，将该曲线绕点O顺时针旋转45°得到曲线C2，点N是由曲线C2上一点，点M在直线y＝﹣x 上，连接MN、ON，若MN＝ON，△MON的面积为，则k的值为（）A．B．C．﹣2D．﹣1【分析】将直线y＝﹣x和曲线C2绕点O逆时针旋转45°，则直线y＝﹣x与x轴重合，曲线C2与曲线C1重合，即可求解．【解答】解：∵将直线y＝﹣x和曲线C2绕点O逆时针旋转45°后直线y＝﹣x与x轴重合，∴旋转后点N落在曲线C1上，点M落在x轴上，如图所示，设点M和点N的对应点分别为点M'和N'，过点N'作N'P⊥x轴于点P，连接ON'，M'N'，∵MN＝ON，∴M'N'＝ON'，M'P＝OP，∴S△MON＝2S△PN'O＝2×＝|k|＝，∵k＜0，∴k＝﹣．故选：B．9．（2023•西安二模）如图，在平面直角坐标系中，直线y＝﹣x+1与x轴，y轴分别交于点A，B，与反比例函数的图像在第二象限交于点C，若AB＝BC，则k的值为﹣2．【分析】过点C作CH⊥x轴于点H．求出点C的坐标，可得结论．【解答】解：过点C作CH⊥x轴于点H．∵直线y＝﹣x+1与x轴，y轴分别交于点A，B，∴A（1，0），B（0，1），∴OA＝OB＝1，∵OB∥CH，∴△AOB∽△AHC，∴，∴＝＝1，∴OA＝OH＝1，∴CH＝2OB＝2，∴C（﹣1，2），∵点C在y＝的图像上，∴k＝﹣2，故答案为：﹣2．10．（2023•双流区模拟）如图，已知一次函数的图像与反比例函数图像交于A，B两点．若AC∥x轴，且AC＝BC，则△ABC面积的最小值为4．【分析】由题意设点A的坐标为（m，m+b），点B的坐标为（n，n+b），即可推出m+n＝﹣，mn＝﹣3，利用勾股定理求得AB2＝4b2+16，进而推出S△ABC ＝AB•CT＝AB2＝b2+4，利用二次函数的性质即可求得△ABC的面积有最小值为4．【解答】解：由题意设点A的坐标为（m，m+b），点B的坐标为（n，n+b），联立，得x2+3bx﹣9＝0，∴m+n＝﹣，mn＝﹣3，∴AB2＝（m﹣n）2+（m+b﹣n﹣b）2＝（m﹣n）2＝[（m+n）2﹣4mn]＝4b2+16，如图，过点C作CT⊥AB于点T，∵AC＝BC，∴AT＝BT＝AB，由一次函数可知，∠CAB＝30°，∴CT＝AT＝AB，∴S△ABC＝AB•CT＝AB2＝b2+4，∴当b＝0时，△ABC的面积有最小值为4，故答案为：4．11．（2023•青羊区模拟）如图，在平面直角坐标系中，一次函数y＝3x与反比例函数的图像交于A，B两点，C是反比例函数位于第一象限内的图像上的一点，作射线CA交y轴于点D，连接BC，BD，若，△BCD的面积为30，则k＝6．【分析】作CF⊥y于点I，BF⊥x，交CI的延长线于点F，作AE⊥CF于点E，设BC交y轴于点M，设A（m，3m），则B（﹣m，﹣3m），k＝3m2，设点C的横坐标为a，则C （a，），可证明tan∠CAE＝tan∠CBF＝，则∠CAE＝∠CBF，即可推导出∠CDM ＝∠CMD，则CD＝CM，所以＝＝＝，则CI＝4FI，所以a＝4m，C（4m，），由＝tan∠CMD＝tan∠CBF＝，得DI＝MI＝3m，则DM＝6m，于是得×6m ×m+×6m×4m＝30，则m2＝2，所以k＝3m2＝6．【解答】解：作CF⊥y于点I，BF⊥x，交CI的延长线于点F，作AE⊥CF于点E，设BC交y轴于点M，∵直线y＝3x经过原点，且与双曲线y＝交于A，B两点，∴点A与点B关于原点对称，设A（m，3m），则B（﹣m，﹣3m），k＝3m2，设点C的横坐标为a，则C（a，），F（﹣m，），∵tan∠CAE＝＝＝，tan∠CBF＝＝＝，∴tan∠CAE＝tan∠CBF，∴∠CAE＝∠CBF，∵AE∥BF∥DM，∠CAE＝∠CDM，∠CBF＝∠CMD，∴∠CDM＝∠CMD，∴CD＝CM，∵＝＝＝，∴CI＝4FI，∴a＝4m，∴C（4m，），∵＝tan∠CMD＝tan∠CBF＝＝＝，∴DI＝MI＝CI＝×4m＝3m，∴DM＝DI+MI＝6m，∵DM•FI+DM•CI＝S△BCD＝30，∴×6m×m+×6m×4m＝30，∴m2＝2，∴k＝3m2＝3×2＝6，故答案为：6．12．（2023•余姚市校级模拟）如图，点A在y＝（x＞0）的图像上，点B，C在y＝（x ＜0）的图像上（C在B左边），直线AB经过原点O，直线AC交y轴于点M，直线BC 交x轴于点N．则＝；＝m，＝n，则＝．【分析】作AD⊥y轴交y轴于D，BE⊥x轴交x轴于E，CF⊥x轴交x轴于F，CG⊥y 轴交y轴于G，再设点A的坐标为（a，），点B的坐标为（b，），点C的坐标为（c，），从而可以表示出AD＝a，OE＝﹣bCG＝﹣c，CF＝﹣，BE＝﹣，再根据三角形相似的判定定理得出△BEO∽△ODA，△CGM∽△ADM，△NCF∽△NBE，可分别表示出OA：OB，MC：MA，NB：NC，再由直线AB经过原点O，可以表示出及的值，最后代入即可得到答案．【解答】解：如图所示，作AD⊥y轴交y轴于D，BE⊥x轴交x轴于E，CF⊥x轴交x 轴于F，CG⊥y轴交y轴于G，设点A的坐标为（a，），点B的坐标为（b，），点C的坐标为（c，），则AD＝a，OE＝﹣b，CG＝﹣c，CF＝﹣，BE＝﹣，∵BE⊥x轴，∴BE∥y轴，∴∠EBO＝∠BOG，∵∠BOG＝∠DOA，∴∠EBO＝∠DOA，∵AD⊥y轴，∴∠BEO＝∠ODA＝90°，∴△BEO∽△ODA，∴OA：OB＝AD：OE＝﹣，∵AD⊥y轴，CG⊥y轴，∴△CGM∽△ADM，∴＝＝﹣＝m，∵BE⊥x，CF⊥x轴，∴△NCF∽△NBE，∴＝＝＝＝n，∴＝＝﹣，∵直线AB经过原点O，∴＝，＝，∴＝，＝，由图像可知，a＞0，c＜b＜0，∴＝﹣，＝﹣，∴＝﹣＝，＝﹣＝，故答案为：；．13．（2023•岳阳一模）如图，已知正比例函数y1＝x的图像与反比例函数y2＝的图像相交于点A（3，n）和点B．（1）求n和k的值；（2）请结合函数图像，直接写出不等式x﹣＜0的解集；（3）如图，以AO为边作菱形AOCD，使点C在x轴正半轴上，点D在第一象限，双曲线交CD于点E，连接AE、OE，求△AOE的面积．【分析】（1）先把点A（3，n）代入正比例函数解析式求出n的值，再把求出的点A坐标代入反比例函数解析式即可求出k值；（2）根据正比例函数和反比例函数都是关于原点成中心对称的，可得出点B的坐标，然后根据图像即可写出解集；（3）根据题意作出辅助线，然后求出OA的长，根据菱形的性质求出OC的长，可推出，然后求出菱形的面积即可求出△AOE的面积．【解答】解：（1）把点A（3，n）代入正比例函数可得：n＝4，∴点A（3，4），把点A（3，4）代入反比例函数，可得：k＝12；（2）∵点A与点B是关于原点对称的，∴点B（﹣3，﹣4），∴根据图像可得，不等式x﹣＜0的解集为：x＜﹣3或0＜x＜3；（3）如图所示，过点A作AG⊥x轴，垂足为G，∵A（3，4），∴OG＝3，AG＝4在Rt△AOG中，AO＝＝5∵四边形AOCD是菱形，∴OC＝OA＝5，，∴．14．（2023•锦江区模拟）如图，在平面直角坐标系xOy中，一次函数y＝2x+b的图像与x 轴交于点A（﹣2，0），与反比例函数交于点B（1，m）．（1）求反比例函数的表达式；（2）点M为反比例函数在第一象限图像上的一点，过点M作x轴垂线，交一次函数y ＝2x+b图像于点N，连接BM，若△BMN是以MN为底边的等腰三角形，求△BMN的面积；（3）点P为反比例函数图像上一点，连接PB，若∠PBA＝∠BAO，求点P的坐标．【分析】（1）用待定系数法即可求解；（2）若△BMN是以MN为底边的等腰三角形，则点B在MN的中垂线上，进而求解；（3）取AB的中点M，过点M作MH⊥AB交x轴于点H，点M是AB的中点且MH⊥AB，则∠PBA＝∠BAO，进而求解．【解答】解：（1）将点A的坐标代入一次函数表达式得：0＝﹣4+b，解得：b＝4，即一次函数的表达式为：y＝2x+4，当x＝1时，y＝2x+4＝6，则点B（1，6），将点B的坐标代入反比例函数表达式得：k＝1×6＝6，即反比例函数表达式为：y＝；（2）设点N的坐标为（t，2t+4），则点M（t，），若△BMN是以MN为底边的等腰三角形，则点B在MN的中垂线上，则（2t+4+）＝6，解得：t＝1（舍去）或3，则点M、N的坐标分别为：（3，10）、（3，2），则△BMN的面积＝MN•（x M﹣x B）＝（10﹣2）×（3﹣1）＝8；（3）取AB的中点M，过点M作MH⊥AB交x轴于点H，∵点M是AB的中点且MH⊥AB，则∠PBA＝∠BAO，由中点坐标公式得，点M（﹣，3），在Rt△AMH中，由AB的表达式知，tan∠BAO＝2，则tan∠MHA＝，则直线MH表达式中的k值为﹣，则直线MH的表达式为：y＝﹣（x+）+3，令y＝﹣（x+）+3＝0，则x＝，即点H（，0），由点B、H的坐标得，直线BH的表达式为：y＝﹣x+，联立y＝﹣x+和y＝并解得：x＝1（舍去）或，则点P的坐标为：（，）．。

一、反比例函数真题与模拟题分类汇编（难题易错题）1．如图．一次函数y=x+b的图象经过点B（﹣1，0），且与反比例函数（k为不等于0的常数）的图象在第一象限交于点A（1，n）．求：（1）一次函数和反比例函数的解析式；（2）当1≤x≤6时，反比例函数y的取值范围．【答案】（1）解：把点B（﹣1，0）代入一次函数y=x+b得： 0=﹣1+b，∴b=1，∴一次函数解析式为：y=x+1，∵点A（1，n）在一次函数y=x+b的图象上，∴n=1+1，∴n=2，∴点A的坐标是（1，2）．∵反比例函数的图象过点A（1，2）．∴k=1×2=2，∴反比例函数关系式是：y=（2）解：反比例函数y= ，当x＞0时，y随x的增大而减少，而当x=1时，y=2，当x=6时，y= ，∴当1≤x≤6时，反比例函数y的值：≤y≤2【解析】【分析】（1）根据题意首先把点B（﹣1，0）代入一次函数y=x+b求出一次函数解析式，又点A（1，n）在一次函数y=x+b的图象上，再利用一次函数解析式求出点A的坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出当x=1，x=6时的y值，即可得到答案．2．心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y 随时间x（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？【答案】（1）解：设线段AB所在的直线的解析式为y1=k1x+20，把B（10，40）代入得，k1=2，∴y1=2x+20．设C、D所在双曲线的解析式为y2= ，把C（25，40）代入得，k2=1000，∴当x1=5时，y1=2×5+20=30，当，∴y1＜y2∴第30分钟注意力更集中．（2）解：令y1=36，∴36=2x+20，∴x1=8令y2=36，∴，∴∵27.8﹣8=19.8＞19，∴经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目．【解析】【分析】（1）根据一次函数和反比例函数的应用，用待定系数法求出线段AB所在的直线的解析式，和C、D所在双曲线的解析式；把x1=5时和进行比较得到y1＜y2，得出第30分钟注意力更集中；（2）当y1=36时，得到x1=8，当y2=36，得到，由27.8﹣8=19.8＞19，所以经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目.3．抛物线y= +x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；（3）若射线NM交x轴于点P，且PA•PB= ，求点M的坐标．【答案】（1）解：y= x2+x+m= （x+2）2+（m﹣1）∴顶点坐标为（﹣2，m﹣1）∵顶点在直线y=x+3上，∴﹣2+3=m﹣1，得m=2；（2）解：过点F作FC⊥NB于点C，∵点N在抛物线上，∴点N的纵坐标为： a2+a+2，即点N（a， a2+a+2）在Rt△FCN中，FC=a+2，NC=NB﹣CB= a2+a，∴NF2=NC2+FC2=（ a2+a）2+（a+2）2，=（ a2+a）2+（a2+4a）+4，而NB2=（ a2+a+2）2，=（ a2+a）2+（a2+4a）+4∴NF2=NB2，NF=NB（3）解：连接AF、BF，由NF=NB，得∠NFB=∠NBF，由（2）的思路知，MF=MA，∴∠MAF=∠MFA，∵MA⊥x轴，NB⊥x轴，∴MA∥NB，∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°，∴2∠MAF+2∠NBF=180°，∠MAF+∠NBF=90°，∵∠MAB+∠NBA=180°，∴∠FBA+∠FAB=90°，又∵∠FAB+∠MAF=90°，∴∠FBA=∠MAF=∠MFA，又∵∠FPA=∠BPF，∴△PFA∽△PBF，∴ = ，PF2=PA×PB= ，过点F作FG⊥x轴于点G，在Rt△PFG中，PG= = ，∴PO=PG+GO= ，∴P（﹣，0）设直线PF：y=kx+b，把点F（﹣2，2）、点P（﹣，0）代入y=kx+b，解得k= ，b= ，∴直线PF：y= x+ ，解方程 x2+x+2= x+ ，得x=﹣3或x=2（不合题意，舍去），当x=﹣3时，y= ，∴M（﹣3，）．【解析】【分析】（1）利用配方法将二次函数化成顶点式，写出顶点坐标，由顶点再直线y=x+3上，建立方程求出m的值。

中考数学反比例函数专题训练（含答案）一、反比例函数的图象与性质1.已知反比例函数的解析式为y＝( |a|－2 ) / x，则a 的取值范围是( )A. a ≠2B. a ≠－2C. a ≠±2D. a＝±22.反比例函数y＝－3 / x，下列说法不正确的是( )A. 图象经过点(1，－3)B. 图象位于第二、四象限C. 图象关于直线y＝x 对称D. y 随x 的增大而增大3.下列各点中，与点(－3，4) 在同一个反比例函数图象上的点的是( )A. (2，－3)B. (3，4)C. (2，－6)D. (－3，－4)4.点M(a，2a) 在反比例函数y＝8 / x 的图象上，那么a 的值是( )A. 4B. －4C. 2D. ±25.如果反比例函数y＝(a－2) / x ( a 是常数) 的图象在第一、三象限，那么a 的取值范围是( )A. a＜0B. a＞0C. a＜2D. a＞26.若点A(－3，y1)，B(－2，y2)，C(1，y3) 都在反比例函数y＝－12 / x 的图象上，则y1，y2，y3 的大小关系是( )A. y2＜y1＜y3B. y3＜y1＜y2C. y1＜y2＜y3D. y3＜y2＜y17.反比例函数y＝k / x 的图象经过点A(－1，2)，则当x＞1 时，函数值y 的取值范围是( )A. y＞－1B. －1＜y＜0C. y＜－2D. －2＜y＜08.若点A(a，b) 在反比例函数y＝3 / x 的图象上，则代数式ab－1 的值为________．9.反比例函数y＝(2m－1)xm2－2，x＞0时，y 随着x 的增大而增大，则m 的值是________.10.已知一个反比例函数的图象位于第二、四象限内，点P(x0，y0) 在这个反比例函数的图象上，且x0y0＞－4.请你写出这个反比例函数的表达式__________．(写出符合题意的一个即可)11.已知A(x1，y1)，B(x2，y2) 都在反比例函数y＝－2 / x 的图象上．若x1x2＝－4，则y1y2 的值为________．12.已知A(1，m)，B(2，n) 是反比例函数y＝k/x 图象上的两点，若m－n＝4，则k 的值为________．13.已知反比例函数的图象经过三个点A(－4，－3)、B(2m，y1)、C(6m，y2)．若y1－y2＝4，则m 的值为________．14.已知反比例函数y＝m / x 在其所在象限内y 随x 的增大而减小，点P(2－m，m＋1) 是该反比例函数图象上一点，则m 的值为________．15.已知A(x1，y1)，B(x2，y2) 是反比例函数y＝k / x 图象上的两点，且x1＋x2＝－2，x1·x2＝2，y1＋y2＝－4/3，则k＝________．16.已知点A(x1，y1)、B(x2，y2) 是反比例函数y＝k/x 图象上的两点，且(x1－x2)(y1－y2)＝9，3x1＝2x2，则k 的值为________．17.在平面直角坐标系xOy 中，点A(a，b) (a＞0，b＞0) 在双曲线y＝k1/x 上，点A 关于x 轴的对称点B 在双曲线y＝k2/x 上，则k1＋k2 的值为________．18.反比例函数y＝k/x 的图象上有一点P(2，n)，将点P 向右平移1 个单位，再向下平移1 个单位得到点Q，若点Q 也在该函数的图象上，则k＝________．19.已知A、B 两点分别在反比例函数y＝(2m－3) / x ( m ≠3/2 ) 和y＝(3m－2) / x ( m ≠2/3) 的图象上，且点A 与点B 关于y 轴对称，则m 的值为________．【参考答案】二、反比例函数与几何图形或一次函数结合1.若一次函数y＝ax＋6 (a≠0) 的图象与反比例函数y＝3/x 的图象只有一个交点，则a 的值为________．2.若直线y＝－x＋m 与双曲线y＝n/x (x＞0) 交于A(2，a)，B(4，b) 两点，则mn 的值为________．3.一次函数y1＝－x＋6 与反比例函数y2＝8/x (x＞0) 的图象如图所示，当y1＞y2 时，自变量x 的取值范围是________．4. 如图，在平面直角坐标系中，直线y＝－x＋2 与反比例函数y＝1/x 的图象有唯一公共点．若直线y＝－x＋b 与反比例函数y＝1/x 的图象没有公共点，则b 的取值范围是________.5.如图，过x 轴的正半轴上任意一点P，作y 轴的平行线，分别与反比例函数y＝3/x (x＞0)，y＝－6/x (x＞0) 的图象相交于点A，B，若C 为y 轴上任意一点，连接AC，BC，则△ABC 的面积为________．6.如图，矩形ABCD 的顶点A，C 在反比例函数y＝k/x (k＞0，x＞0) 的图象上，若点A 的坐标为(3，4)，AB＝2，AD∥x 轴，则点C 的坐标为________．7.如图，正方形ABCD 的边长为2，点B 与原点O 重合，与反比例函数y＝k/x 的图象交于E、F 两点，若△DEF 的面积为9/8，则k 的值为________．8.如图，已知反比例函数y＝4/x 的图象经过Rt△OAB 斜边OB 的中点D，与直角边AB 相交于点C，则△OBC 的面积为________．9.如图，反比例函数y＝k/x 的图象经过平行四边形ABCD 对角线的交点P，已知点A、C、D 在坐标轴上，BD⊥DC，平行四边形ABCD 的面积为6，则k＝________．10.如图，点A，C 分别是正比例函数y＝x 的图象与反比例函数y＝4/x 的图象的交点，过A 点作AD⊥x 轴于点D，过C 点作CB⊥x 轴于点B，则四边形ABCD 的面积为________．11.如图，点A 是反比例函数y＝－8/x 图象上的一点，过点A 的直线与y 轴交于点B，与反比例函数y＝k/x (x＞0) 的图象交于点C、D.若AB＝BC＝CD，则k 的值为________．12.如图，△OAC 和△BAD 都是等腰直角三角形，∠ACO＝∠ADB＝90°，反比例函数y＝k/x 在第一象限的图象经过点B，若OA2－AB2＝8，则k 的值为________．【参考答案】。

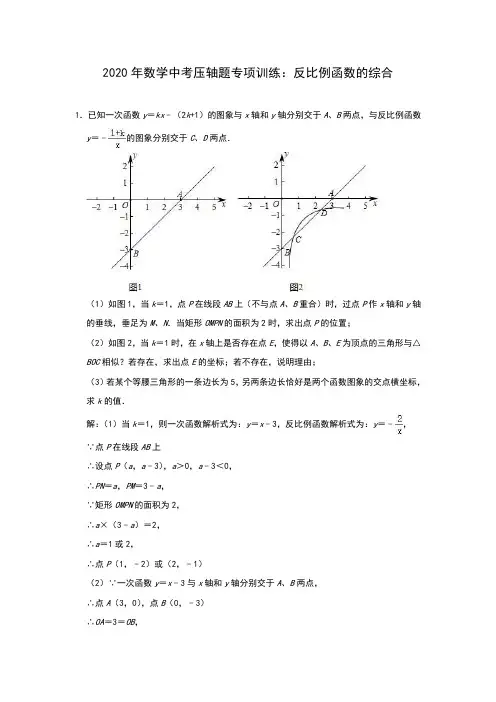
2020年数学中考压轴题专项训练：反比例函数的综合1．已知一次函数y＝kx﹣（2k+1）的图象与x轴和y轴分别交于A、B两点，与反比例函数y＝﹣的图象分别交于C、D两点．（1）如图1，当k＝1，点P在线段AB上（不与点A、B重合）时，过点P作x轴和y轴的垂线，垂足为M、N．当矩形OMPN的面积为2时，求出点P的位置；（2）如图2，当k＝1时，在x轴上是否存在点E，使得以A、B、E为顶点的三角形与△BOC相似？若存在，求出点E的坐标；若不存在，说明理由；（3）若某个等腰三角形的一条边长为5，另两条边长恰好是两个函数图象的交点横坐标，求k的值．解：（1）当k＝1，则一次函数解析式为：y＝x﹣3，反比例函数解析式为：y＝﹣，∵点P在线段AB上∴设点P（a，a﹣3），a＞0，a﹣3＜0，∴PN＝a，PM＝3﹣a，∵矩形OMPN的面积为2，∴a×（3﹣a）＝2，∴a＝1或2，∴点P（1，﹣2）或（2，﹣1）（2）∵一次函数y＝x﹣3与x轴和y轴分别交于A、B两点，∴点A（3，0），点B（0，﹣3）∴OA＝3＝OB，∴∠OAB＝∠OBA＝45°，AB＝3，∵x﹣3＝﹣∴x＝1或2，∴点C（1，﹣2），点D（2，﹣1）∴BC＝＝，设点E（x，0），∵以A、B、E为顶点的三角形与△BOC相似，且∠CBO＝∠BAE＝45°，∴，或，∴，或＝，∴x＝1，或x＝﹣6，∴点E（1，0）或（﹣6，0）（3）∵﹣＝kx﹣（2k+1），∴x＝1，x＝，∴两个函数图象的交点横坐标分别为1，，∵某个等腰三角形的一条边长为5，另两条边长恰好是两个函数图象的交点横坐标，∴1＝，或5＝∴k＝2．如图，已知直线y＝kx+b与反比例函数y＝（x＞0）的图象交于A（1，4）、B（4，1）两点，与x轴交于C点．（1）求一次函数与反比例函数的解析式；（2）根据图象直接回答：在第一象限内，当x取何值时，一次函数值大于反比例函数值？（3）点P是y＝（x＞0）图象上的一个动点，作PQ⊥x轴于Q点，连接PC，当S△CPQ ＝S时，求点P的坐标．△CAO解：（1）把A （1，4）代入y ＝（x ＞0），得m ＝1×4＝4，∴反比例函数为y ＝；把A （1，4）和B （4，1）代入y ＝kx +b 得， 解得：， ∴一次函数为y ＝﹣x +5．（2）根据图象得：当1＜x ＜4时，一次函数值大于反比例函数值；（3）设P （m ，），由一次函数y ＝﹣x +5可知C （5，0），∴S △CAO ＝＝10，∵S △CPQ ＝S △CAO ，∴S △CPQ ＝5， ∴|5﹣m |•＝5，解得m ＝或m ＝﹣（舍去）， ∴P （，）．3．如图，直线y ＝kx +b （b ＞0）与抛物线y ＝x 2相交于点A （x 1，y 1），B （x 2，y 2）两点，与x 轴正半轴相交于点D ，于y 轴相交于点C ，设△OCD 的面积为S ，且kS +8＝0．（1）求b 的值．（2）求证：点（y 1，y 2）在反比例函数y ＝的图象上．（1）解：∵直线y＝kx+b（b＞0）与x轴正半轴相交于点D，于y轴相交于点C，∴D（0，b），C（﹣，0）∴由题意得OD＝b，OC＝﹣，∴S＝∴k•（）+8＝0，∴b＝4（b＞0）；（2）证明：∵，∴，∴x1•x2＝﹣16∴，∴点（y1，y2）在反比例函数y＝的图象上．4．如图，双曲线y＝上的一点A（m，n），其中n＞m＞0，过点A作AB⊥x轴于点B，连接OA．（1）已知△AOB的面积是3，求k的值；（2）将△AOB绕点A逆时针旋转90°得到△ACD，且点O的对应点C恰好落在该双曲线上，求的值．解：（1）∵双曲线y＝上的一点A（m，n），过点A作AB⊥x轴于点B，∴AB＝n，OB＝m，又∵△AOB的面积是3，∴mn＝3，∴mn＝6，∵点A在双曲线y＝上，∴k＝mn＝6；（2）如图，延长DC交x轴于E，由旋转可得△AOB≌△ACD，∠BAD＝90°，∴AD＝AB＝n，CD＝OB＝m，∠ADC＝90°，∵AB⊥x轴，∴∠ABE＝90°，∴四边形ABED是矩形，∴∠DEB＝90°，∴DE＝AB＝n，CE＝n﹣m，OE＝m+n，∴C（m+n，n﹣m），∵点A，C都在双曲线上，∴mn＝（m+n）（n﹣m），即m2+mn﹣n2＝0，方程两边同时除以n2，得+﹣1＝0，解得＝，∵n＞m＞0，∴＝．5．在平面直角坐标系xOy 中，对于点P （a ，b ）和实数k （k ＞0），给出如下定义：当ka +b ＞0时，将以点P 为圆心，ka +b 为半径的圆，称为点P 的k 倍相关圆．例如，在如图1中，点P （1，1）的1倍相关圆为以点P 为圆心，2为半径的圆．（1）在点P 1（2，1），P 2（1，﹣3）中，存在1倍相关圆的点是 P 1 ，该点的1倍相关圆半径为 3 ．（2）如图2，若M 是x 轴正半轴上的动点，点N 在第一象限内，且满足∠MON ＝30°，判断直线ON 与点M 的倍相关圆的位置关系，并证明．（3）如图3，已知点A 的（0，3），B （1，m ），反比例函数y ＝的图象经过点B ，直线l 与直线AB 关于y 轴对称．①若点C 在直线l 上，则点C 的3倍相关圆的半径为 3 ．②点D 在直线AB 上，点D 的倍相关圆的半径为R ，若点D 在运动过程中，以点D 为圆心，hR 为半径的圆与反比例函数y ＝的图象最多有两个公共点，直接写出h 的最大值．解：（1）由题意知，k＝1，（2，1），a＝2，b＝1，针对于P1∴ka+b＝2+1＝3＞0，∴点P（2，1）的1倍相关圆为以点P为圆心，3为半径的圆，1（1，﹣3），a＝1，b＝﹣3，针对于P2∴ka+b＝1﹣3＝﹣2＜0，∴点P（1，﹣3）不存在1倍相关圆2；3；故答案为：P1（2）如图2中，结论：直线ON与点M的倍相关圆的位置关系是相切．理由：设点M的坐标为（n，0），过M点作MP⊥ON于点P，∴点M的倍相关圆半径为n．∴OM＝n．∵MP⊥ON，∴∠OPM＝90°，∵∠MON＝30°，∴MP＝OM＝n，∴点M的倍相关圆的半径为MP，∴直线ON与点M的倍相关圆相切；（3）①如图3中，记直线AB与x轴的交点为E，直线l与x轴的交点为F，∵B（1，m）在反比例函数y＝的图象上，∴m＝6，∴B（1，6）∵A（0，3），∴直线AB的解析式为y＝3x+3，令y＝0，则3x+3＝0，∴x＝﹣1，∴E（﹣1，0），∵直线l是直线AB关于y轴对称，∴点F与点E关于y轴对称，∴F（1，0），∴直线l的解析式为y＝﹣3x+3，∵点C在直线l上，∴设C（c，﹣3c+3），由题意知，k＝3，∴3c+（﹣3c+3）＝3，∴点C的3倍相关圆的半径是3，故答案为：3；②∵点D在直线AB上，设D（d，3d+3），由题意知，k＝，∴R＝d+（3d+3）＝d+3＞0，∴d＞﹣．6．如图，在平面直角坐标系中，直线y＝2x+2与x轴、y轴分别交于A，B两点，与反比例函数y＝的图象交于点M，且B为AM的中点．（1）求反比例函数y＝的表达式；（2）过B做x轴的平行线，交反比例函数y＝图象于点C，连接MC，AC．求△AMC的面积．解：（1）过点M作MH⊥y轴，垂足为H．∵AB＝MB，∠MHB＝∠AOB，∠MBH＝∠ABO，∴△ABO≌△MBH（AAS），∴BH＝BO，MH＝AO，∵直线y＝2x+2与x轴，y轴分别交于A，B两点，∴当y＝0时，x＝﹣1．当x＝0时，y＝2．∴A（﹣1，0），B（0，2）．∴BH＝BO＝2，MH＝AO＝1．∴M（1，4）．把M（1，4）代入中，得k＝4．∴反比例函数的解析式为．（2）∵AB＝BM，∴S△ABC ＝S△BCM．∵点C在反比例函数图象上，且BC∥x轴，∴点C纵坐标为2．把y＝2代入，得x＝2．∴点C坐标为（2，2），∴，∴S△AMC＝4．7．已知：如图，在平面直角坐标系xOy中，点A（0，2），正方形OABC的顶点B在函数y ＝（k≠0，x＜0）的图象上，直线l：y＝﹣x+b与函数y＝（k≠0，x＜0）的图象交于点D，与x轴交于点E．（1）求k的值；（2）横、纵坐标都是整数的点叫做整点．①当一次函数y＝﹣x+b的图象经过点A时，直接写出△DCE内的整点的坐标；②若△DCE内的整点个数恰有6个，结合图象，求b的取值范围．解：（1）依题意知：B（﹣2，2），∴反比例函数解析式为y＝﹣．∴k的值为﹣4；（2）①∵一次函数y＝﹣x+b的图象经过点A，∴b＝2，∴一次函数的解析式为y＝﹣x+2，解得，，，∴D（1﹣，1+），E（2，0），∴△DCE内的整点的坐标为（﹣1，1），（﹣1，2），（0，1）；②当b＝2时，△DCE内有3个整点，当b＝3时，△DCE内有6个整点，∴b的取值范围是2＜b≤3．8．如图，在平面直角坐标系xOy中，函数y＝（x＜0）的图象经过点A（﹣1，6）．（1）求k的值；（2）已知点P（a，﹣2a）（a＜0），过点P作平行于x轴的直线，交直线y＝﹣2x﹣2于点M，交函数y＝（x＜0）的图象于点N．①当a＝﹣1时，求线段PM和PN的长；②若PN≥2PM，结合函数的图象，直接写出a的取值范围．解：（1）∵函数y＝（x＜0）的图象经过点A（﹣1，6）．∴k＝﹣1×6＝﹣6．（2）①当a＝﹣1时，点P的坐标为（﹣1，2）．∵直线y＝﹣2x﹣2，反比例函数的解析式为y＝﹣，PN∥x轴，∴把y＝2代入y＝﹣2x﹣2，求得x＝﹣2，代入y＝﹣求得x＝﹣3，∴M（﹣2，2），N（﹣3，2），∴PM＝1，PN＝2．②∵当a＝﹣1或a＝﹣3时，PN＝2PM，∴根据图象PN≥2PM，a的取值范围为a≤﹣3或﹣1≤a＜0．9．如图，已知点D在反比例函数y＝的图象上，过点D作DB⊥y轴，垂足为B（0，3），直线y＝kx+b经过点A（5，0），与y轴交于点C，且BD＝OC，OC：OA＝2：5．（1）求反比例函数y＝和一次函数y＝kx+b的表达式；（2）连结AD，求∠DAC的正弦值．解：（1）∵BD＝OC，OC：OA＝2：5，点A（5，0），点B（0，3），∴OA＝5，OC＝BD＝2，OB＝3，又∵点C在y轴负半轴，点D在第二象限，∴点C的坐标为（0，﹣2），点D的坐标为（﹣2，3）．∵点D（﹣2，3）在反比例函数的图象上，∴a＝﹣2×3＝﹣6，∴反比例函数的表达式为．将A（5，0）、C（0，﹣2）代入y＝kx+b，得，解得：，∴一次函数的表达式为．（2）∵OA＝BC＝5，OC＝BD＝2，∠DBC＝∠AOC＝90°，∴△BDC≌△OCA（SAS），∴∠DCB＝∠OAC，DC＝CA，∴∠DCA＝90°，∴△DCA是等腰直角三角形，∴∠DAC＝45°，∴．10．如图，A为反比例函数y＝（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝4．连接OA、AB，且OA＝AB＝2．（1）求k的值；（2）过点B作BC⊥OB，交反比例函数y＝（x＞0）的图象于点C．①连接AC，求△ABC的面积；②在图上连接OC交AB于点D，求的值．解：（1）过点A作AH⊥x轴，垂足为点H，AH交OC于点M，如图所示．∵OA＝AB，AH⊥OB，∴OH＝BH＝OB＝2，∴AH＝＝＝6，∴点A的坐标为（2，6）．∵A为反比例函数y＝图象上的一点，∴k＝2×6＝12；（2）①∵BC⊥x轴，OB＝4，点C在反比例函数y＝上，∴BC＝＝3．∵AH⊥OB，∴AH∥BC，∴点A到BC的距离＝BH＝2，＝×3×2＝3；∴S△ABC②∵BC⊥x轴，OB＝4，点C在反比例函数y＝上，∴BC＝＝3．∵AH∥BC，OH＝BH，∴MH＝BC＝，∴AM＝AH﹣MH＝．∵AM∥BC，∴△ADM∽△BDC，∴＝．11．如图，反比例函数y＝的图象与一次函数y＝x+1的图象相交于点A（2，3）和点B．（1）求反比例函数的解析式和点B的坐标；（2）连接OA，OB，求△AOB的面积．（3）结合图象，请直接写出使反比例函数值小于一次函数值的自变量x的取值范围．解：（1）把A（2，3）代入得，∴k＝6．∴反比例函数的解析式为．联立解得或，∴点B的坐标为（﹣3，﹣2）．（2）设直线AB与y轴交于点C．可知C点的坐标为（0，1），∴OC＝1．∴．（3）当﹣3＜x＜0或x＞2时，反比例函数值小于一次函数值．12．如图1，直线y＝x与双曲线y＝交于A，B两点，根据中心对称性可以得知OA＝OB．（1）如图2，直线y＝2x+1与双曲线y＝交于A，B两点，与坐标轴交点C，D两点，试证明：AC＝BD；（2）如图3，直线y＝ax+b与双曲线y＝交于A，B两点，与坐标轴交点C，D两点，试问：AC＝BD还成立吗？（3）如果直线y＝x+3与双曲线y＝交于A，B两点，与坐标轴交点C，D两点，若DB+DC ≤5，求出k的取值范围．解：（1）如图1中，作AE⊥x轴于E，BF⊥y轴于F，连接EF，AF，BE．∵AE∥y轴，∴S△AOE ＝S△AEF＝，∵BF∥x轴，∴S△BEF ＝S△OBF＝，∴S△AEF ＝S△BEF，∴AB∥EF，∴四边形ACFE，四边形BDEF都是平行四边形，∴AC＝EF，BD＝EF，∴AC＝BD．（2）如图1中，如图1中，作AE⊥x轴于E，BF⊥y轴于F，连接EF，AF，BE．∵AE∥y轴，∴S△AOE ＝S△AEF＝，∵BF∥x轴，∴S△BEF ＝S△OBF＝，∴S△AEF ＝S△BEF，∴AB∥EF，∴四边形ACFE，四边形BDEF都是平行四边形，∴AC＝EF，BD＝EF，∴AC＝BD．（3）如图2中，∵直线y＝x+3与坐标轴交于C，D，∴C（0，3），D（3，0），∴OC＝OD＝3，CD＝3，∵CD+BD≤5，∴BD≤2，当BD＝2时，∵∠CDO＝45°，∴B（1，2），此时k＝2，观察图象可知，当k≤2时，CD+BD≤5，13．综合与探究如图1，平面直角坐标系中，直线l：y＝2x+4分别与x轴、y轴交于点A，B．双曲线y ＝（x＞0）与直线l交于点E（n，6）．（1）求k的值；（2）在图1中以线段AB为边作矩形ABCD，使顶点C在第一象限、顶点D在y轴负半轴上．线段CD交x轴于点G．直接写出点A，D，G的坐标；（3）如图2，在（2）题的条件下，已知点P是双曲线y＝（x＞0）上的一个动点，过点P作x轴的平行线分别交线段AB，CD于点M，N．请从下列A，B两组题中任选一组题作答．我选择①组题．A．①当四边形AGNM的面积为5时，求点P的坐标；②在①的条件下，连接PB，PD．坐标平面内是否存在点Q（不与点P重合），使以B，D，Q为顶点的三角形与△PBD全等？若存在，直接写出点Q的坐标；若不存在，说明理由．B．①当四边形AGNM成为菱形时，求点P的坐标；②在①的条件下，连接PB，PD．坐标平面内是否存在点Q（不与点P重合），使以B，D，Q为顶点的三角形与△PBD全等？若存在，直接写出点Q的坐标；若不存在，说明理由．解：（1）由已知可得A（﹣2，0），B（0，4），E（1，6），∴k＝6；（2）∵AB⊥BC，∴BC的解析式为y＝﹣x+4，联立，∴C（2，3），∵CD＝AB＝2，∴D（0，﹣1），∴CD的解析式为y＝2x﹣1，∴G（，0）；（3）A①设P（m，），∵MN∥x轴，∴M（﹣2，），N（+，），∴MN＝，∵四边形AGNM的面积为5，∴×＝5，∴m＝3，∴P（3，2）；②Q（3，1）、Q（﹣3，1）、Q（﹣3，2）时B，D，Q为顶点的三角形与△PBD全等．B①∵四边形AGNM成为菱形，MN＝AM，∴＝∴m＝，∴P（，）；②Q（﹣，）、Q（，3﹣）、Q（﹣，3﹣）时B，D，Q为顶点的三角形与△PBD全等．14．如图，直线AB与反比例函数y＝（x＞0）的图象交于点A，已知点A（3，4），B（0，﹣2），点C是反比例函数y＝（x＞0）的图象上的一个动点，过点C作x轴的垂线，交直线AB于点D．（1）求反比例函数的解析式；（2），求△ABC的面积；（3）在点C运动的过程中，是否存在点C，使BC＝AC？若存在，请求出点C的坐标；若不存在，请说明理由．解：（1）∵反比例函数y＝（x＞0）的图象经过点A（3，4），∴k＝xy＝3×4＝12，∴反比例函数的解析式为：y＝；（2）作AE⊥y轴于点E，交CD于点F，则BE∥CD，∴＝＝，∵点A的坐标为（3，4），∴EF＝1，FA＝2，∴点F的横坐标为1，∴点C的坐标为（1，12），设直线AB的解析式为：y＝kx+b，则，解得，，∴直线AB的解析式为：y＝2x﹣2，则点D的坐标为：（1，0），即CD＝12，∴△ABC的面积＝×12×1+×12×2＝18；（3）不存在，理由如下：设点C的坐标为（m，），∵BC＝AC，∴m2+（+2）2＝（3﹣m）2+（﹣4）2，整理得，6m2﹣21m+144＝0，△＝212﹣4×6×144＜0，则此方程无解，∴点C不存在．15．如图，在平面直角坐标系第一象限中，已知点A坐标为（1，0），点D坐标为（1，3），点G坐标为（1，1），动点E从点G出发，以每秒1个单位长度的速度匀速向点D方向运动，与此同时，x轴上动点B从点A出发，以相同的速度向右运动，两动点运动时间为t（0＜t＜2），以AD、AB分别为边作矩形ABCD，过点E作双曲线交线段BC于点F，作CD 中点M，连接BE、EF、EM、FM．（1）当t＝1时，求点F的坐标．（2）若BE平分∠AEF，则t的值为多少？（3）若∠EMF为直角，则t的值为多少？解：（1）当t＝1时， EG＝1×1＝1＝AB∴点E（1，2）设双曲线解析式：y＝∴k＝1×2＝2∴双曲线解析式：y＝∵OB＝OA+AB＝2，∴当x＝2时，y＝1，∴点F（2，1）（2）∵EG＝AB＝t，∴点E（1，1+t），点B（1+t，0）设双曲线解析式：y＝∴m＝1+t∴双曲线解析式：y＝当x＝1+t时，y＝1∴点F（1+t，1）∵BE平分∠AEF∴∠AEB＝∠BEF，∵AD∥BC∴∠AEB＝∠EBF＝∠BEF∴EF＝BF＝1∴＝t＝1∴t＝（3）延长EM，BC交于点N，∵EG＝AB＝t，∴点E（1，1+t），点B（1+t，0）∴DE＝AD﹣AE＝3﹣（1+t）＝2﹣t，设双曲线解析式：y＝∴n＝1+t∴双曲线解析式：y＝当x＝1+t时，y＝1∴点F（1+t，1）∵AD∥BC，∴∠ADC＝∠NCD，∠DEM＝∠MNC，且DM＝CM，∴△DEM≌△CNM（AAS）∴EM＝MN，DE＝CN＝2﹣t，∵CF＝BC﹣BF＝2∴NF＝CF+CN＝2﹣t+2＝4﹣t，∵∠EMF为直角，∴∠EMF＝∠NMF＝90°，且EM＝MN，MF＝MF，∴△EMF≌△NMF（SAS），∴EF＝NF，∴t＝4﹣t∴t＝4﹣4。

2021年九年级中考数学一轮复习专题《反比例函数综合》1．在平面直角坐标系xOy中，直线l：y＝ax+b与双曲线y＝交于点A（1，m）和B （﹣2，﹣1）．点A关于x轴的对称点为点C．（1）①求k的值和点C的坐标；②求直线l的表达式；（2）过点B作y轴的垂线与直线AC交于点D，经过点C的直线与直线BD交于点E．若30°≤∠CED≤45°，直接写出点E的横坐标t的取值范围．2．如图，Rt△ABP的直角顶点P在第四象限，顶点A、B分别落在反比例函数y＝图象的两支上，且PB⊥x轴于点C，PA⊥y轴于点D，AB分别与x轴，y轴相交于点F 和E．已知点B的坐标为（1，3）．（1）填空：k＝；（2）证明：CD∥AB；（3）当四边形ABCD的面积和△PCD的面积相等时，求点P的坐标．3．如图，在平面直角坐标系中，直线y＝+n（n＜0）与坐标轴交于A、B两点，与y ＝（x＞0）交于点E，过点E作EF⊥x轴，垂足为F，且△OAB∽△FEB，相似比为．（1）若，求m的值；（2）连接OE，试探究m与n的数量关系，并直接写出直线OE的解析式．4．如图，反比例函数y＝（k＞0）的图象与正比例函数y＝x的图象交于A、B两点（点A在第一象限）．（1）当点A的横坐标为2时，求k的值；（2）若k＝12，点C为y轴正半轴上一点，∠ACB＝90°，①求△ACB的面积；②以A、B、C、D为顶点作平行四边形，直接写出第四个顶点D的坐标．5．如图，在平面直角坐标系xOy中，线段AB两个端点的坐标分别为A（1，2），B（4，2），以点O为位似中心，相似比为2，在第一象限内将线段AB放大得到线段CD．已知点B在反比例函数y＝（x＞0）的图象上．（1）求反比例函数的解析式，并画出图象；（2）判断点C是否在此函数图象上；（3）点M为直线CD上一动点，过M作x轴的垂线，与反比例函数的图象交于点N．若MN≥AB，直接写出点M横坐标m的取值范围．6．如图，一次函数y＝kx+1的图象与反比例函数的图象交于点A（2，a），点B为x轴正半轴上一点，过B作x轴的垂线交反比例函数的图象于点C，交一次函数的图象于点D．（1）求a的值及一次函数y＝kx+1的表达式；（2）若BD＝10，求△ACD的面积．7．如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），点A在x轴的正半轴上，直线y＝x﹣1．交边AB、OA于点D、M，反比例函数y＝（x＞0）的图象经过点D，与BC的交点为N．（1）求BN的长．（2）点P是直线DM上的动点（点P不与点D、点M重合），连接PB、PC、MN，当△BCP的面积等于四边形ABNM的面积时，求点P的坐标．（3）在（2）的条件下，连接CP，以CP为边作矩形CPEF，使矩形的对角线的交点G 落在直线DM上，请直接写出点G的坐标．8．如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（，1）在反比例函数y＝的图象上．（1）求反比例函数y＝的表达式；（2）求△AOB的面积；（3）在坐标轴上是否存在一点P，使得以O、B、P三点为顶点的三角形是等腰三角形若存在，请直接写出所有符合条件的点P的坐标；若不存在，简述你的理由．9．在平面直角坐标系xOy中，已知一次函数y＝ax+b（a≠0）与反比例函数的图象交于点A（1，m）和B（﹣2，﹣1）．点A关于x轴的对称点为点C．（1）求这两个函数的表达式．（2）直接写出关于x的不等式的解．（3）过点B作y轴的垂线与直线AC交于点D，经过点C的直线与直线BD交于点E，且30°≤∠CED≤60°，直接写出点E的横坐标t的取值范围．10．已知，如图，在平面直角坐标系xOy中，双曲线与直线y＝2x都经过点A（2，m）．（1）求k与m的值；（2）此双曲线又经过点B（n，2），点C是y轴的负半轴上的一点，且点C到x轴的距离是2，联结AB、AC、BC，①求△ABC的面积；②点E在y轴上，△ACE为等腰三角形，请直接写出点E的坐标．参考答案1．解：（1）①∵点B（﹣2，﹣1）在双曲线y＝上，∴k＝﹣2×（﹣1）＝2，∴反比例函数解析式为y＝，∵点A（1，m）在双曲线y＝上，∴m＝2，∴A（1，2），∵点A关于x轴的对称点为点C，∴C（1，﹣2）；②∵直线l：y＝ax+b经过点A（1，2）和B（﹣2，﹣1），∴，∴，Array∴直线l的解析式为y＝x+1；（2）如图，∵点A关于x轴的对称点为点C，∴AC∥y轴，∵BD⊥y轴，∴∠BDC＝90°，D（1，﹣1），∵C（1，﹣2），∴CD＝1，①当点E在点D左侧时，当∠CED＝45°时，DE＝CD＝1，∴t＝0，当∠CE'D＝30°时，DE'＝CD＝，∴t＝1﹣，∵30°≤∠CED≤45°，∴1﹣≤t≤0；②当点E在点D右侧时，同①的方法得，2≤t≤1+，即：1﹣≤t≤0或2≤t≤1+．2．（1）解：∵B点（1，3）在反比例函数y＝的图象，∴k＝1×3＝3．故答案为：3．（2）证明：∵反比例函数解析式为，∴设A点坐标为（a，）．∵PB⊥x轴于点C，PA⊥y轴于点D，∴D点坐标为（0，），P点坐标为（1，），C点坐标为（1，0），∴PB＝3﹣，PC＝﹣，PA＝1﹣a，PD＝1，∴，，∴．又∵∠P＝∠P，∴△PDC∽△PAB，∴∠CDP＝∠A，∴CD∥AB．（3）解：∵四边形ABCD 的面积和△PCD 的面积相等，∴S△PAB ＝2S △PCD ，∴×（3﹣）×（1﹣a ）＝2××1×（﹣），整理得：（a ﹣1）2＝2，解得：a 1＝1﹣，a 2＝1+（舍去），∴P 点坐标为（1，﹣3﹣3）．3．解：（1）当时，直线方程是y ＝﹣，当x ＝0时，y ＝﹣，即A （0，﹣），则OA ＝．当y ＝0时，x ＝1，即B （1，0），则OB ＝1．∵△OAB ∽△FEB ，相似比为，∴EF ＝2OA ＝1，BF ＝2OB ＝2，OF ＝OB +BF ＝1+2＝3，∴点E 的坐标为（3，1）．∵点E 在反比例函数y ＝（x ＞0）的图象上，∴m ＝3×1＝3；（2）∵直线y ＝+n （n ＜0）与坐标轴交于A 、B 两点，∴当x ＝0时，y ＝n ，即A （0，n ），则OA ＝﹣n ．当y ＝0时，x ＝﹣2n ，即B （﹣2n ，0），则OB ＝﹣2n ．∵△OAB ∽△FEB ，相似比为，∴EF ＝2OA ＝﹣2n ，BF ＝2OB ＝﹣4n ，OF ＝OB +BF ＝﹣6n ，∴点E 的坐标为（﹣6n ，﹣2n ）．∵点E 在反比例函数y ＝（x ＞0）的图象上，∴m ＝（﹣6n ）•（﹣2n ）＝12n 2；由点E 的坐标为（﹣6n ，﹣2n ）得到直线OE 的解析式为：y ＝x ．4．解：（1）当x ＝2时，y ＝×2＝，∴点A 坐标为（2，），∵点A 在反比例函数y ＝（k ＞0）的图象上，∴k ＝2×＝3，（2）①∵k ＝12，∴反比例函数解析式为y ＝， 联立方程组可得：，解得：或，∴点A（4，3），点B（﹣4，﹣3），∴AO＝BO＝5，又∵∠ACB＝90°，∴CO＝AO＝BO＝5，∴点C（0，5），∴△ACB的面积＝×5×4+×5×4＝20；②设点D坐标为（x，y），若AB为对角线，则四边形ACBD是平行四边形，∴AB与CD互相平分，∴，，∴x＝0，y＝﹣5，∴点D（0，﹣5）；若AC为对角线，则四边形ABCD是平行四边形，∴AC与BD互相平分，∴，，∴x＝8，y＝11，∴点D（8，11）；若BC为对角线，则四边形ACDB是平行四边形，∴BC与AD互相平分，∴，＝，∴x＝﹣8，y＝﹣1，∴点D（﹣8，﹣1），综上所述：点D坐标为（0，﹣5）或（8，11）或（﹣8，﹣1）．5．解：（1）将点B（4，2）代入反比例函数y＝中，得，∴k＝8，Array∴反比例函数的解析式为y＝，图象如图1所示，（2）∵以点O为位似中心，相似比为2，在第一象限内将线段AB放大得到线段CD，且A（1，2），∴C（1×2，2×2），即C（2，4），由（1）知，反比例函数解析式为y＝，当x＝2时，y＝＝4，∴点C在反比例函数图象上；（3）∵以点O为位似中心，相似比为2，在第一象限内将线段AB放大得到线段CD，且B（4，2），∴D（4×2，2×2），即D （8，4），由（2）知，C （2，4），∴直线CD 的解析式为y ＝4，∵点M 的横坐标为m ，则M （m ，4），N （m ，），∴MN ＝|4﹣|，∵A （1，2），B （4，2），∴AB ＝3，∵MN ≥AB ，∴|4﹣|≥3，∴m ≥8或m ≤，即0＜m ≤或m ≥8．6．解：（1）把点A （2，a ）代入反比例函数得，a ＝＝4， ∴点A （2，4），代入y ＝kx +1得，4＝2k +1，解得k ＝∴一次函数的表达式为； （2）∵BD ＝10，∴D 的纵坐标为10， 把y ＝10代入得，x ＝6，∴OB ＝6，当x ＝6代入y ＝得，y ＝，即BC ＝，∴CD ＝BD ﹣BC ＝10﹣＝，∴S △ACD ＝×（6﹣2）＝．7．解：（1）依题意，得：点A 的坐标为（3，0），点B 的坐标为（3，3）． 当x ＝3时，y ＝x ﹣1＝2，∴点D 的坐标为（3，2）．将D （3，2）代入y ＝，得：2＝，解得：m ＝6，∴反比例函数解析式为y ＝．当y ＝3时，＝3，解得：x ＝2，∴点N 的坐标为（2，3），∴BN ＝3﹣2＝1．（2）当y ＝0时，x ﹣1＝0，解得：x ＝1，∴点M 的坐标为（1，0），∴AM ＝2，∴S 梯形ABNM ＝（BD +AM ）•AB ＝．设点P 的坐标为（x ，x ﹣1）（x ≠1，x ≠3），∴S △BCP ＝BC •|3﹣y P |＝|4﹣x |＝，解得：x 1＝1（舍去），x 2＝7，∴点P 的坐标为（7，6）．（3）过点C 作CF ⊥CP ，交DM 于点F ，如图2所示．设点F 的坐标为（n ，n ﹣1）．∵点C 的坐标为（0，3），点P 的坐标为（7，6），∴PC 2＝（0﹣7）2+（3﹣6）2＝58，CF 2＝（n ﹣0）2+（n ﹣1﹣3）2＝2n 2﹣8n +16，PF2＝（n ﹣7）2+（n ﹣1﹣6）2＝2n 2﹣28n +98．∵∠PCF ＝90°，∴PF 2＝PC 2+CF 2，即2n 2﹣28n +98＝58+2n 2﹣8n +16，解得：n ＝，∴点F 的坐标为（，）．又∵点G 为线段PF 的中点，∴点G 的坐标为（，）．8．解：（1）将A （，1）代入y ＝，得：1＝， 解得：k ＝，∴反比例函数的表达式为y ＝． （2）∵点A 的坐标为（，1），AB ⊥x 轴于点C ，∴OC ＝，AC ＝1，∴OA ＝＝2＝2AC ，∴∠AOC ＝30°．∵OA ⊥OB ，∴∠AOB ＝90°，∴∠B ＝∠AOC ＝30°，∴AB ＝2OA ＝4，∴S △AOB ＝AB •OC ＝×4×＝2． （3）在Rt △AOB 中，OA ＝2，∠AOB ＝90°，∠ABO ＝30°，∴OB ＝＝2． 分三种情况考虑：①当OP ＝OB 时，如图2所示，∵OB ＝2，∴OP ＝2，∴点P 的坐标为（﹣2，0），（2，0），（0，﹣2），（0，2）；②当BP ＝BO 时，如图3，过点B 做BD ⊥y 轴于点D ，则OD ＝BC ＝AB ﹣AC ＝3， ∵BP ＝BO ，∴OP ＝2OC ＝2或OP ＝2OD ＝6，∴点P 的坐标为（2，0），（0，﹣6）；③当PO ＝PB 时，如图4所示．若点P 在x 轴上，∵PO ＝PB ，∠BOP ＝60°，∴△BOP 为等边三角形，∴OP ＝OB ＝2，∴点P 的坐标为（2，0）；若点P 在y 轴上，设OP ＝a ，则PD ＝3﹣a ， ∵PO ＝PB ，∴PB2＝PD2+BD2，即a2＝（3﹣a）2+12，解得：a＝2，∴点P的坐标为（0，﹣2）．综上所述：在坐标轴上存在一点P，使得以O、B、P三点为顶点的三角形是等腰三角形，点P的坐标为（﹣2，0），（2，0），（0，﹣2），（0，2），（0，﹣6），（0，﹣2）．9．解：（1）∵点B（﹣2，﹣1）在反比例函数y＝的图象上，∴k＝﹣2×（﹣1）＝2，∴反比例函数的表达式为y＝；当x＝1时，m＝＝2，∴点A的坐标为（1，2）．将A（1，2），B（﹣2，﹣1）代入y＝ax+b，得：，解得：，∴一次函数的表达式为y＝x+1．（2）观察函数图象，可知：当x＜﹣2或0＜x＜1时，一次函数图象在反比例函数图象的下方，∴不等式的解为x≤﹣2或0＜x≤1．（3）∵点A的坐标为（1，2），点A，C关于x轴对称，∴点C的坐标为（1，﹣2）．∵点B的坐标为（﹣2，﹣1），BD⊥AC，∴点D的坐标为（1，﹣1），∴CD＝﹣1﹣（﹣2）＝1．在Rt△CDE中，CD＝1，∠CDE＝90°，30°≤∠CED≤60°，∴cot∠CED＝，∴≤DE≤，∴1﹣≤t≤1﹣或1+≤t≤1+．10．解：（1）∵直线y ＝2x 经过点A （2，m ），∴m ＝2×2＝4，∴点A 的坐标为（2，4）．∵双曲线经过点A （2，4）， ∴4＝，∴k ＝8．（2）①由（1）得：双曲线的表达式为y ＝．∵双曲线y ＝经过点B （n ，2），∴2＝，∴n ＝4，∴点B 的坐标为（4，2）．∵点C 是y 轴的负半轴上的一点，且点C 到x 轴的距离是2， ∴点C 的坐标为（0，﹣2），∴AB ＝＝2，BC ＝＝4，AC ＝＝2．∵（2）2+（4）2＝（2）2，∴AB 2+BC 2＝AC 2，∴∠ABC ＝90°，∴S △ABC ＝AB •BC ＝×2×4＝8．②设点E 的坐标为（0，a ），∴AE 2＝（0﹣2）2+（a ﹣4）2＝a 2﹣8a +20，CE 2＝[a ﹣（﹣2）]2＝a 2+4a +4，AC 2＝40．分三种情况考虑，如图2所示．（i ）当AE ＝AC 时，a 2﹣8a +20＝40，解得：a 1＝﹣2（舍去），a 2＝10，∴点E 1的坐标为（0，10）；（ii ）当CE ＝AC 时，a 2+4a +4＝40，解得：a 3＝﹣2+2，a 4＝﹣2﹣2，∴点E 2的坐标为（0，﹣2+2），点E 3的坐标为（0，﹣2﹣2）； （iii ）当CE ＝AE 时，a 2+4a +4＝a 2﹣8a +20，解得：a ＝，∴点E 4的坐标为（0，）．综上所述：点E 的坐标为（0，10），（0，﹣2+2），（0，﹣2﹣2）或（0，）．。