第一章 有理数 复习小结
- 格式:ppt
- 大小:958.00 KB
- 文档页数:18


第一章有理数期末复习一、正数:大于0的数叫做正数。
负数:正数前加上符号“—”(负)的数叫做负数。
注意:0既不是正数,也不是负数;0是正数和负数的分界。
考点题目:1.如果80m表示向东走80m,那么-60m表示_____________2.在跳远测试中,合格的标准是4.00m,小明跳出了3.96m,记做-0.04m,小强的成绩被记做+0.18m,则小强跳了______m3.洗衣粉包装袋上有:“净重:300±5g”,请说明这段文字的含义袋号 1 2 3 4 5净重 303 298 300 294 305根据上面的数据解释这5袋洗衣粉的净重是否合格。
4.飞机在距地面800m的高空做飞行表演,它第一次上升了200m,第二次下降了300m,第三次又上升了-100米,此时它距地面多高?二、有理数:整数和分数统称为有理数。
整数:正整数,0,负整数统称为整数;分数:正分数,负分数统称为分数注意:小数可以化为分数,所以把小数看成分数;百分数也是分数。
正有理数:正整数,正分数有理数{ 0负有理数:负整数,负分数有理数{整数:正整数负整数 0分数:正分数负分数含有“π”的数均不是有理数。
考点题目:1.“0”的意义:①0是整数,也是有理数。
②0不是正数也不是负数。
③0是自然数2.把下列各数填在相应的集合中:-22,-π,-5%,92 ,-0.66……,0.121121112……,3.14正整数集合:。
负整数集合:。
负分数集合:。
有理数集合:。
负有理数集合:。
三、数轴:规定了单位长度,原点,正方向的直线。
考点题目:1.数轴上表示表示3的点和表示-6的点之间的距离是_____2.数轴上-3与2之间有___个整数,有____个有理数。
3.点A为数轴上表示-2的点,当点A沿数轴移动4个单位长度时,它所表示的数是_____4.在数轴上到原点的距离等于2的点所表示的数为_______5.把数轴上表示2的点移动5个单位长度后,所得的对应的点表示的数是_______6.画出数轴并标出下列各数对应的点四、相反数:只有符号不同的两个数叫做互为相反数注意:a和-a互为相反数(a表示任意一个数,正数,负数,0)0的相反数是0;互为相反数的两个数相加得0考点题目:1.-3的相反数是_______;0的相反数是_______;2.化简各数的符号:-(-5)=_______ +(+5)=_______ +(-5)=_______(+5)=________3.如果a=-a,那么表示数a的点在数轴的位置是_______4.如果a+2的相反数是-8,那么a=_______如果a的相反数是-9,那么a=_______5.一个数在数轴上所对应的点向左移动8个单位后,得到表示他的相反数的点,这个数是_______6.若a+2的相反数是-8,那么a=_______五、绝对值:数轴上表示数a的点与原点的距离叫做a的绝对值,记作|a|。


第一章有理数知识点、考点、难点总结归纳大家好,今天我们来聊聊有理数这个知识点。
有理数是我们日常生活中经常会遇到的一种数,它们可以表示为两个整数的比值,比如1/2、3/4等等。
有理数在数学中非常重要,因为它们可以帮助我们解决很多问题。
有理数有哪些知识点呢?下面我们就来一一梳理。
我们来说说有理数的基本概念。
有理数包括正有理数、负有理数和零。
正有理数就是大于零的有理数,比如1/2、3/4等等;负有理数就是小于零的有理数,比如-1/2、-3/4等等;零是有理数,但它既不大于零也不小于零。
我们来看一下有理数的运算。
有理数的加法、减法、乘法和除法都很简单,我们可以通过以下几个例子来说明。
例一:正有理数相加。
假设我们有两个正有理数a和b,那么它们的和就是a+b。
例如,1/2+1/3=5/6。
例二:正有理数相减。
假设我们有两个正有理数a和b,那么它们的差就是a-b。
例如,3/4-1/2=1/4。
例三:正有理数相乘。
假设我们有两个正有理数a和b,那么它们的积就是a*b。
例如,1/2*3/4=3/8。
例四:正有理数相除。
假设我们有两个正有理数a和b(b≠0),那么它们的商就是a/b。
例如,3/4÷1/2=3/2=1.5。
有理数的运算还有很多其他的形式,比如负有理数的加法、减法、乘法和除法等。
但是这些都比较复杂,我们以后再学吧。
除了基本的运算之外,有理数还有一些重要的性质和定理。
比如,有理数的相反数是它的负倒数;有理数的绝对值是它的大小;有理数的平方根有两个,一个是正的,一个是负的;有理数的小数部分可以无限精确地表示为分数形式等等。
这些性质和定理在解决一些实际问题时非常有用。
我们来说说有理数的解题方法。
其实,有理数的解题方法和其他类型的题目差不多。
我们需要先理解题目的意思,然后根据题目的要求选择合适的方法进行计算。
有时候,我们还需要运用一些特殊的技巧来简化计算过程。
只要我们掌握了有理数的基本知识和解题方法,就可以轻松地解决很多数学问题了!今天我们就来聊到这里。
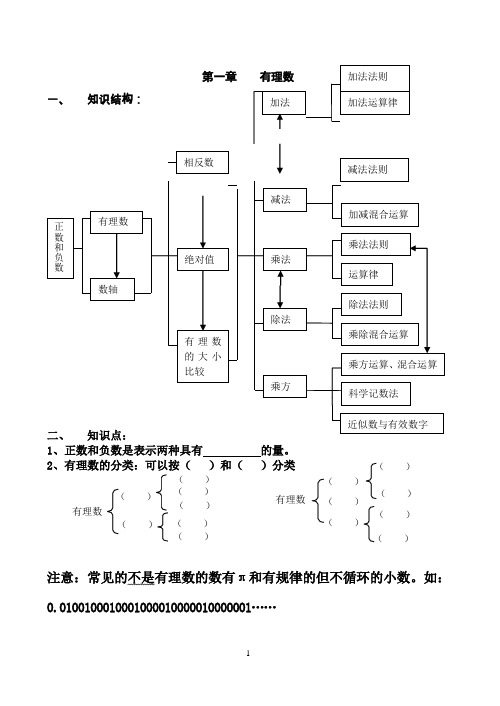
第一章有理数 一、 知识结构:二、 知识点: 1、正数和负数是表示两种具有 的量。
2、有理数的分类:可以按( )和( )分类注意:常见的不是有理数的数有π和有规律的但不循环的小数。
如:0.0100100010001000010000010000001……3、数轴三要素是 、 、 。
数轴是 线。
4、数轴上表示一个数的点到原点的 叫这个数的绝对值。
绝正数和负数 有理数 数轴 绝对值 有理数的大小比较 减法乘法 除法乘方 加减混合运算乘法法则 运算律除法法则乘除混合运算乘方运算、混合运算科学记数法加法 加法法则 加法运算律 减法法则近似数与有效数字 相反数 有理数 ( ) ( ) ( ) ( ) ( ) ( ) ( ) 有理数 ( )( ) ( ) ( )( ) ( ) ( )对值具有非负性,即┃a┃ 0.互为相反数的两个数的绝对值。
若表示两个非负数的式子和为0(或这两个式子互为相反数),则这两个式子都等于。
即非负条件式。
如:若(x-3)2+┃x+y+7┃=0,求y x的值。
5、数轴上的两点之间的距离就是表示这两个点的数的差的绝对值:表示数a的点A与表示数b的点B之间的距离AB=︱a-b︱或AB=︱b -a︱。
与表示数m的点的距离为a(a>0)的点有两个:表示的数是m±a.6、数轴上在两侧且到的距离相等的两个点表示的两个数互为相反数(几何定义),只有符号不同的两个数互为相反数(代数定义)。
0的相反数是,a的相反数是。
求一个数的相反数就是在这个数前添“”号后再化简。
7、互为倒数的两个数的乘积等于。
互为倒数的两个数符号。
互为负倒数的两个数的乘积等于。
互为相反数的两个数的商等于。
8、有理数的绝对值的取法:(a>0) (a≥0) (a>0)|a|= (a=0)或|a|= 或|a|=___(a<0) (a<0) (a≤0)9、有理数的大小比较:异号两数大;两个负数大的反而小;0大于而小于;数轴上原点边的数大于边的数。

人教版七年级数学上册第一章有理数全章知识点归纳人教版七年级数学上册第一章有理数全章知识点归纳一、知识要点1、正数和负数大于的数叫做正数。
在正数前面加上负号“-”的数叫做负数。
数既不是正数,也不是负数,是正数与负数的分界。
在同一个问题中,分别用正数与负数表示的量具有相反的意义。
2、有理数凡能写成分数形式的数,都是有理数,整数和分数统称有理数。
注意:即不是正数,也不是负数;-a不一定是负数,如:-(-2)=4,这个时候的a=-2.不是有理数;正有理数包括正整数和正分数,负有理数包括负整数和负分数。
3、数轴【重点】用一条直线上的点表示数,这条直线叫做数轴。
它满足以下要求:1.在直线上任取一个点表示数,这个点叫做原点;2.通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;3.选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3…;从原点向左,用类似的方法依次表示-1,-2,-3…数轴的三要素:原点、正方向、单位长度。
画数轴的步骤:一画(画一条直线并选取原点);二取(取正反向);三选(选取单位长度);四标(标数字)。
数轴的规范画法:是条直线,数字在下,字母在上。
注意:所有的有理数都可以用数字上的点表示,但是数轴上的所有点并不都表示有理数。
4、相反数只有符号不同的两个数叫做互为相反数。
a的相反数是-a;a-b的相反数是b-a;a+b的相反数是-(a+b)=-a-b;非零数的相反数的商为-1;相反数的绝对值相等。
一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,他们分别在原点的两侧,表示a和-a,我们说这两点关于原点对称。
3、相反数的概念a和-a互为相反数。
一个数的相反数是指,正数的相反数是负数,负数的相反数是正数。
每个数都有它自己的相反数。
4、相反数的运用在任意一个数前面添加“-”号,这个新的数就表示原数的相反数。
如果两个数a和b互为相反数,那么a+b=0;反之,如果a+b=0,则a和b互为相反数。
第一章《有理数》复习总结有理数是整数和分数的统称,包括正数、负数和零。
有理数可以表示为p/q的形式,其中p和q都是整数,且q不等于0。
p称为分子,q称为分母。
1.有理数的大小比较:(1)对于同号的有理数,绝对值越大,数值越大;(2)对于异号的有理数,正数大于负数,绝对值越小,数值越大。
2.有理数的加减乘除:(1)加法:拆分有理数,按照整数部分和小数部分相加;(2)减法:将减数变为相反数,再进行加法运算;(3)乘法:分别计算分子和分母的乘积,然后化简;(4)除法:将除数变为倒数,再进行乘法运算。
3.有理数的约分和化简:(1)约分:将分子和分母同时除以最大公因数,使得分数不可再约分;(2)化简:将带有分数线的有理数化为最简形式。
4.有理数的绝对值:(1)正数的绝对值是其本身;(2)负数的绝对值是其相反数;(3)零的绝对值是零。
5.有理数的相反数:(1)正数的相反数是负数;(2)负数的相反数是正数;(3)零的相反数是零。
6.计算混合数的值:(1)将整数部分和小数部分分开,分别计算;(2)将结果相加或相减,得到最终的结果。
7.有理数的乘方:(1)有理数的整数次方,将底数连乘或连除相应次数;(2)底数是分数,将底数化为整数的形式进行计算。
8.有理数的乘法逆元:(1)有理数的乘法逆元是其倒数;(2)除零外,任意非零有理数的乘法逆元存在。
9.有理数的混合运算:(1)先进行括号内的运算,再进行乘除法运算,最后进行加减法运算;(2)若有多个加法或减法运算,按照从左到右的顺序进行。
10.有理数在坐标轴上的表示:(1)正数表示点在原点的右侧;(2)负数表示点在原点的左侧;(3)零表示点在原点。
有理数在数学中有着广泛的应用,比如在数轴上定位、计算中的加减乘除、分数和小数的运算等。
学好有理数不仅需要掌握各种运算规则和性质,还需要大量的练习和实践。
通过不断的练习和思考,可以提高解决实际问题的能力,培养思维和逻辑思维能力。
总之,有理数作为数学的一个重要概念,是我们平日生活中接触最多的数的形式。
第一章有理数小结与复习教学目标1.复习本章的重点内容,整理本章知识,形成知识体系,体会研究问题的思路和方法.2.进一步提高计算能力及有条理地思考和表达的能力.教学重难点【学习重点】有理数的概念及有理数的运算.【学习难点】有理数的运算,数形结合思想的运用.教学方法 :分层教学,讲授、练习相结合教学过程设计:一、情景导入 生成问题本章知识结构图:二、自学互研 生成能力一 有理数的相关概念典例1:在下列四个数中,在-1和2之间的数是( )A .0B .-2C .-3D .3典例2.:如果a 与1互为相反数,则|a +2|等于( )A .2B .-2C .1D .-1典例3:在数2,-1,-4.5,0,-32,3.1中,正数有( ) A .1个B .2个C .3个D .4个典例4:若x 的相反数为1,则|x -4|等于( )A .2B .-3C .-5D .5二 有理数的运算典例5:计算:(1)-23+(-0.1)2÷⎝⎛⎭⎫-14-(-2)3×⎝⎛⎭⎫-14;(2)⎣⎡⎦⎤2-⎝⎛⎭⎫1-0.3×13×[3-(-2)2]; (3)⎝⎛⎭⎫-76×(-15)×⎝⎛⎭⎫-67×15;(4)⎪⎪⎪⎪12-1+⎪⎪⎪⎪13-12+⎪⎪⎪⎪14-13+…+⎪⎪⎪⎪11000-1999;(5)14×5+15×6+16×7+17×8.三 科学记数法和近似数典例6:用科学记数法表示下列各数.(1)3500000= ; (2)100300000= .典例7:下列由四舍五入法得到的近似数,各精确到哪一位?(1)132.4;(2)0.0572;(3)2.58万.典例8:用科学记数法表示下列各数:(1)70600= ; (2)-3480000= .典例9:用四舍五入法对下列各数取近似数.(1)0.00786≈ (精确到万分位); (2)81.65≈ (精确到个位).三、交流展示 生成新知【交流预展】1.将阅读教材时“生成的问题”和通过“自主学习、合作探究”得出的“结论”展示在各小组的小黑板上.并将疑难问题也板演到黑板上,再一次通过小组间就上述疑难问题相互释疑.2.各小组由组长统一分配展示任务,由代表将“问题和结论”展示在黑板上,通过交流“生成新知”.【课堂小结】一 有理数的相关概念二 有理数的运算三 科学记数法和近似数四、检测反馈 达成目标【当堂检测】1.下列交换加数位置的变形中,正确的是( )A .1-4+5-4=1-4+4-5B .1-2+3-4=2-1-4-3C .5.5-4.2-2.5+1.2=5.5-2.5+1.2-4.2D .13+2.3-5-4.3=13+5-2.3-4.32.在股票交易中,买、卖一次各需交8‰的各种费用,某投资者以每股10元的价格买入某种股票1000股,当该股票涨到13元时全部卖出,则该投资者实际盈利为( )A .3000元B .2920元C .2896元D .2816元3.填空:(1)(-81)÷(-3)2×3= ; (2)-32-(-2)3= ;(3)4-(-2)2-32÷(-1)+0×(-5)2= .4.计算:(1)338×⎝⎛⎭⎫813-318÷1124×827; (2)⎝⎛⎭⎫1112-56+78-2324×(-48).。