第一单元有理数小结与复习教案.doc

第一章有理数小结与复习一、引入：本章我们在小学的基础上，进一步认识了负数，使数的范围扩充到有理数，并研究了有理数的加、减、乘、除、乘方的运算，本节课，我们对本章知识作一个系统的归纳、整理。

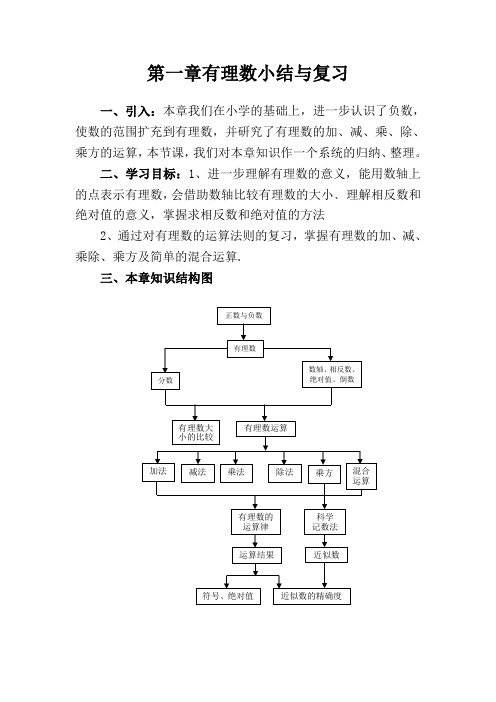
二、学习目标：1、进一步理解有理数的意义，能用数轴上的点表示有理数，会借助数轴比较有理数的大小﹑理解相反数和绝对值的意义，掌握求相反数和绝对值的方法2、通过对有理数的运算法则的复习，掌握有理数的加、减、乘除、乘方及简单的混合运算.三、本章知识结构图四、本章知识点1、有理数可以写成qp (p 、q 是整数，q ≠0)形式；另一方面，形如qp (p 、q 是整数，q ≠0)的数都是有理数有理数的分类 按整、分性分类按正、负性分类注意：分类要有标准，要做到不重复，不遗漏.2、数轴是一条具有原点、正方向、和单位长度的直线。

数轴的三要素：原点、正方向、单位长度数轴是一个很好的工具，它将数与形结合起来了，任何一个有理数都可以用数轴上的时唯一一个点表示出来，数轴上的很多点表示的是有理数．一般地设a 是一个正数则数轴上表示a的点在原点的右边，与原点的距离是a个长度单位；表示一a的点在原点的左边，与原点的距离是a个单位长度3、相反数的意义：只有符号不同的两个数叫做互为相反数.特别地0的相反数是0. 注意：（1）只有符号不同，而不是只要符号不同，（2）相反数是成对出现的，（3）在数轴上表示互为相反数的两个点，分别位于原点的两侧，且与原点的距离相等，这两个点关于原点对称, （4）0的相反数是其本身.一般地:a与-a互为相反数注意：这里的a表示任意一个数，可以是正数，负数，也可以是0，利用相反数的概念可以进行符号简化.如：-（+a）=-a, +(-a)=-a,-(-a)=a.4、绝对值的几何意义：一般地数轴上表示数a的点与原点的距离叫做数a的绝对值，记作│a│绝对值的代数意义：○1文字语言，一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0○2符号语言若a＞0, 则│a│= a若a=0，则│a│= 0若a＜0，则│a│= - a一个数的绝对值是一个非负数，即│a│≥05、有理数的大小比较方法（1）两个正数，绝对值大的这个正数就大；（2）正数大于0，0大于负数，正数大于负数；（3）两个负数，绝对值大的反而小.注意：数轴上表示某数的点，越靠右，这个数就越大.（1）异号两数比较大小，要注意它们的符号；（2）同号两数比较大小，要注意它们的绝对值.（3）在比较有理数的大小之前，要先简化数.6、有理数的运算有理数的加法法则（1）同号两数相加，取相同的符号，并把绝对值相加（2）绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值。

初一数学上册第一章有理数复习教案最新3篇篇一：数学《有理数》教案篇一一、教材分析：（一）教材的地位和作用：本节课的内容是《新人教版七年级数学》教材中的第一章第四节，“有理数的乘除法”是把“有理数乘法”和“有理数除法”的内容进行整合，在“有理数的加减混合运算”之后的一个学习内容。

在本章教材的编排中，“有理数的乘法”起着承上启下的作用，它既是有理数加减的深入学习，又是有理数除法、有理数乘方的基础，在有理数运算中有很重要的地位。

“有理数的乘法”从具体情境入手，把乘法看做连加，通过类比，让学生进行充分讨论、自主探索与合作交流的形式，自己归纳出有理数乘法法则。

通过这个探索的过程，发展了学生观察、归纳、猜测、验证的能力，使学生在学习的过程中获得成功的体验，增强了自信心。

所以本节课的学习具有一定的现实地位。

（二）学情分析：因为学生在小学的学习里已经接触过正数和0的乘除法，对于两个正数相乘、正数与0相乘、两个正数相除、0与正数相除的情况学生已经掌握。

同时由于前面学习了有理数的加减法运算，学生对负数参与运算有了一定的认识，但仍还有一定的困难。

另外，经过前一阶段的教学，学生对数学问题的研究方法有了一定的了解，课堂上合作交流也做得相对较好。

（三）教学目标分析：基于以上的学情分析，我确定本节课的教学目标如下1、知识目标：让学生经历学习过程，探索归纳得出有理数的乘除法法则，并能熟练运用。

2、能力目标：在课堂学习过程中，使学生经历探索有理数乘除法法则的过程，发展观察、猜想、归纳、验证、运算的能力，同时在探索法则的过程中培养学生分类和归纳的数学思想。

3、情感态度和价值观：在探索过程中尊重学生的学习态度，树立学生学习数学的自信心，培养学生严谨的数学思维习惯。

4、教学重点：会进行有理数的乘除法运算。

5、教学难点：有理数乘除法法则的探索与运用。

确定教学目标的理由依据是：新课标中指出课堂教学中应体现知识与技能、过程与方法、情感态度与价值观的三维目标，同时也基于本节内容的地位与作用。

第一章有理数总结教案第一章：有理数总结教案一、教学目标通过本章学习，学生应掌握以下能力：掌握有理数的基本概念，包括正数、负数、整数、分数等。

掌握有理数的四则运算，包括加法、减法、乘法、除法及乘方。

理解并能够运用有理数的性质，如相反数、绝对值等。

能够在实际问题中运用有理数的知识，进行简单的数学建模。

二、教学内容及方法有理数的概念：通过实例引入正数、负数、整数、分数等概念，让学生明确有理数的范围和分类。

有理数的四则运算：通过例题讲解和课堂练习，让学生掌握加法、减法、乘法、除法的运算方法和运算律。

同时，引入乘方的概念，让学生理解其运算规则。

有理数的性质：讲解相反数和绝对值的概念，通过实例让学生理解并运用这些性质。

数学建模：选取一些实际问题，引导学生运用有理数的知识建立数学模型，提高其解决实际问题的能力。

三、教学重点与难点重点：有理数的概念和四则运算。

这些是有理数学习的基础，对于后续的学习至关重要。

难点：有理数的性质理解和运用，特别是绝对值的概念。

需要通过大量的实例和练习帮助学生理解。

四、教学评价与反馈课堂练习：通过课堂练习，检查学生对有理数知识的掌握情况，及时发现并纠正学生的错误。

课后作业：布置适量的有理数练习题，要求学生按时完成，巩固所学知识。

单元测试：进行单元测试，全面了解学生对有理数知识的掌握程度，为后续教学提供依据。

反馈与指导：根据学生的练习、作业和测试情况，进行有针对性的反馈和指导，帮助学生解决学习中遇到的问题。

五、教具和多媒体资源黑板：用于展示例题和重要的概念、公式。

投影仪：用于展示PPT课件，帮助学生更好地理解有理数的概念和运算过程。

教学软件：使用数学教育软件进行辅助教学，如GeoGebra等，可以动态展示数学概念和运算过程。

教学卡片：用于制作各种数学概念的卡片，便于学生进行复习和记忆。

教学模型：如数轴等，可以帮助学生直观理解数学概念和性质。

六、学生活动设计分组讨论：将学生分成小组，让他们在小组内讨论有理数的概念和性质，互相交流学习心得。

第一章《有理数》复习一、基本概念 1.有理数生活中的一些具有相反意义的量： 1.飞机上升500米与下降500米； 2.向东走5米与向西走6米； 3.存入1000元和支出900元。

请你将右图连线：我们可以把一种意义的量规定为正.同时把另一种与它相反意义的量规定为负，分别称它们为 正数和负数。

0既不是正数，也不是负数。

〖练一练〗“一个数,如果不是负数,就是正数。

”这句话对吗，为什么？在小学学过的数（零除外）前面加一个“—”号表示负数！ 在小学学过的数（零除外）前面加一个“+”号表示正数！(通常正号可以省略) 例1 如果温度上升8℃记作 +8,下降3℃记作 －3，那么下列各数分别表示什么？（1）+5 （2）―6.8 (3) 0正数 有理数 0负数1(口答)读出下列各数,它们各是哪一类数?7 ,－7.46 , 0 , +50/7, ―2/3，-2, －7, －8, +1.3, -0.82.填空:(1) 规定赢利为正,某公司去年亏损了 2.5万元,记做____万元,今年盈 利了3.2万元, 记做_____万元;(2)规定海平面以上的海拔高度为正.新疆乌鲁木齐市高于海平面918米,记做海拔____ 米;吐鲁番盆地最低点低于海平面155米,记做海拔____米.例2 下列给出的各数,哪些是正数?哪些是负数?哪些是整数? 哪些是分数?哪些是有理数?―8.4, 22, +17/6, 0.33, 0, ―3/5盈利 存入 增加 运进 上升 涨 输 进球 南失球 赢 支出 跌 亏损 减少 运出 下降 东【选一选】把”存入银行+50元”改成使用负数的说法是( )(A)取出+50元 (B)取出-50元 (C)存入+50元 (D)存入-50元你能解释”前进-50米”的意思吗?〖课内练习〗 1 填空:(1) 汽车在一条南北走向的高速公路上行驶,规定向北行驶的路程为正. 汽车向北行驶75千米,记做____km,(或＿＿km ），汽车向南行驶１００km ，记做＿＿km.(2)如果向银行存入５０元记为５０元，那么－３０．５０元表示＿＿＿＿＿＿＿＿；(3)规定增加的百分比为正，增加２５%记做＿＿，－１２ %表示＿＿＿＿＿＿＿＿＿＿．引进了负数之后，数的范围扩大了整数有理数分数小结①表示大小：②在实际中表示意义相反的量 上升5米记为：5， -8则表示下降8米。

第一章有理数全章教案有理数教学目标〔知识与技能〕1、了解正数、负数的实际意义，会判断一个数是正数还是负数。

2、掌握数轴的画法，能将已知数在数轴上表示出来，能说出数轴上已知点所表示的数。

3、理解相反数、绝对值的几何意义和代数意义，会求一个数的相反数和绝对值.4、会利用数轴和绝对值比较有理数的大小。

5、理解乘方的意义，会进行乘方的计算。

掌握有理数加减、乘除、乘方的混合运算。

6、通过实例进一步感受大数，并能用科学记数法表示；了解近似数和有效数字的概念。

〔过程与方法〕1、经历探索有理数运算法则和运算律的过程，体会类比、转化、数形结合等思想方法.2、培养学生应用数学知识的意识，提高学生运用知识解决实际问题的能力。

〔情感、态度与价值观〕1、通过教学活动，激励学生学习数学的兴趣；使学生感受数学知识与现实世界的联系。

2、给学生渗透辩证唯物主义思想。

重点难点有理数的运算是重点；准确理解负数、绝对值的意义和运算符号的确定是难点。

课时分配1.1正数和负数2课时1.2有理数5课时1.3有理数的加减法3课时1.4有理数的乘除法5课时1.5有理数的乘方4课时本章小结2课时人教版数学第一章有理数全章教案1．1．1 正数和负数的概念〔教学目标〕1、了解负数产生是生活、生产的需要；2、掌握正、负数的概念和表示方法，理解数0表示的量的意义；3、理解具有相反意义的量的含义。

〔重点难点〕正确理解正、负数的概念，数0表示的量的意义和具有相反意义的量是重点；正确理解负数、数0表示的量的意义是难点。

〔教学过程〕一、负数的引入我们知道，数产生于人们实际生产和生活的需要。

[投影1～3：图1.1-1]人们由记数、排序，产生了数1，2，3 ；为了表示“没有”、“空位”引进了数0，测量和分配有时不能得到整数的结果，为此产生了分数和小数。

在生活、生产、科研中经常遇到数的表示与数的运算的问题。

[投影4]（1）北京冬季里某天的温度为－3～3℃，它的确切含义是什么？这一天北京的温差是多少？（2）有三个队参加的足球比赛中，红队胜黄队（4U1），黄队胜蓝队（1U0），蓝队胜红队（1U0），三个队的净胜球分别是2，－2，0，如何确定排名顺序？（3）2022年我国产量比上年增长1.8％，油菜籽产量比上年增长－2.7％，这里的增长－2.7％代表什么意思？上面三个问题中，哪些数的形式与以前学习的数有区别？数－3、－2、－2.7％与以前学习的数有区别。

第1章有理数小结与复习一、教学目标1.复习有理数的意义及其有关概念，其内容包括正负数、有理数、数轴、有理数大小的比 较、相反数与绝对值等，通过复习使学生系统掌握有理数这一章的有关基本概念；2.会运用有理数的运算法则、运算律，熟练进行有理数的运算；3.用四舍五入法，按要求(精确度)确定运算结果；4.会利用计算器进行有理数的简单计算和探索数的规律.二、教学重点、难点重点：1.掌握有理数的概念；2.理解并会用有理数的加、减、乘、除和乘方五种运算法则进行有理数的混合运算；3.学会借助数轴来理解绝对值、有理数比较大小等相关知识；4.理解科学记数法，近似数.难点：准确地掌握有理数的运算顺序和运算中的符号问题.三、教学过程知识梳理一、正数和负数1.小学学过的除0以外的数都是正数.在正数前面加上符号“-”(负)的数叫做负数.2.用正、负数表示具有相反意义的量.二、有理数1.有理数的概念整数和分数统称为有理数.2.有理数的分类(1)按定义分类 (2)按符号分类⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 3.数轴(1)规定了原点、正方向、单位长度的直线叫做数轴.(2)任何一个有理数都可以用数轴上的一个点来表示.4.相反数(1)只有符号不同的两个数叫做互为相反数.(2)互为相反数的两个数到原点的距离相等.5.绝对值(1)一个数在数轴上对应的点到原点的距离叫做这个数的绝对值.(2)一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0.6.有理数大小的比较(1)数轴上表示的两个数，右边的总比左边的大.(2)正数大于0，0大于负数，正数大于负数；两个负数，绝对值大的反而小.三、有理数的运算1.有理数的加法有理数加法法则1.同号两数相加，取相同的符号，并把绝对值相加.2.绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值. 互为相反数的两个数相加得0；3.一个数同0相加，仍得这个数.⎩⎨⎧++=+++=+)()(c b a c b a a b b a 加法的结合律加法的交换律加法的运算律 2.有理数的减法减法法则：减去一个数，等于加上这个数的相反数.3.有理数的乘法乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数与0相乘，都得0.⎪⎩⎪⎨⎧+=+==ac ab c b a bc a c ab ba ab )(:)()(::结合律结合律交换律乘法的运算律 4.有理数的除法除法法则：除以一个不等于0的数，等于乘以这个数的倒数.5.有理数的乘方求几个相同因数的积的运算，叫做乘方.6.有理数的混合运算(1)先乘方，再乘除，最后加减；(2)同级运算，从左到右进行；(3)如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行.四、科学记数法把大于10的数记成a×10n的形式，其中1.1≤a＜102.n为原数的整数位减去1五、近似数1.按照要求取近似数四舍五入到某一位，就说这个近似数精确到那一位.2.由近似数判断精确度考点讲练考点一正、负数的意义例1 如果＋4米表示向东走4米，那么向西走2米记作_____.针对训练1.下列语句中，含有相反意义的两个量是( )A.盈利2千元和收入2千元B.上升8米和前进8米C.存入2千元和取出2千元D.超过2厘米和上涨2厘米2.水位下降9cm记作－9cm，那么水位上升8cm记作_______.考点二正、负数的概念例2 判断:①不带“－”号的数都是正数……………………( )②如果a是正数，那么－a一定是负数…………( )③不存在既不是正数，也不是负数的数…………( )④一个有理数不是正数就是负数…………………( )⑤0℃表示没有温度…………………………………( )方法总结0既不是正数也不是负数，0的相反数是它本身.0不仅能表示没有，而且表示正、负之间的分界值.考点三有理数的分类例3 将下列各数分别填入相应的圈内：3.5，－3.5，0，|－2|，－2，531-，31-，0.5●针对训练3.在2.3，0，＋3，－6，23-，－0.9中，负分数有____个. 考点四 相反数、倒数、绝对值例4 填表：考点五 数轴、有理数比较大小例5 请将下面的数在数轴上表示出来，并将它们用“＞”连接起来.3.5，－3.5，0，－2，53. 解：表示如下3.5＞53＞0＞-2＞-3.5 针对训练4.在数轴上，点A 所表示的数为－2，那么到点A 的距离等于5个单位长度的点所表示的数是_______.5.某日零点，北京、上海、重庆、宁夏的气温分别是－4℃、5℃、6℃、－8℃，当时这四个城市中，气温最低的是( )A.北京B.上海C.重庆D.宁夏考点六 科学记数法例6 将数2 560 000 000km 用科学记数法表示____________m.针对训练6.某城市常住人口总数为563.8万人，用科学记数法表示为____________人.考点七 近似数例7 2017年我国全年出境旅游人数达1.27亿人次.这里的1.27亿精确到______位. 针对训练7.由四舍五入法得到的近似数2.96×105精确到____位，如果精确到万位可写成_________. 考点八 有理数的运算例8 计算 (1) 25.03211813413125.0-⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛++ 解：原式=81+341-381+1132-41=(81-381)+(341-41)+1132=(-3)+3+1132=1132 (2) ()361856543127-⨯⎪⎭⎫ ⎝⎛+-+- 解：原式=-127×(-36)+43×(-36)-65×(-36)+185×(-36) =21+(-27)-(-30)+(-10)=21-27+30-10=14(3) ()⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-÷-1211212 解：原式=-2÷121÷121=-2×12×12=288 (4) ()()2245.0612153222--⎪⎭⎫ ⎝⎛-⨯+⎪⎭⎫ ⎝⎛÷- 解：原式=-16÷(38)2+211×(-61)-(-21)2 =-16×649+(-1211)-41 =-49-1211-41=-1227-1211-123=-1241针对训练8.计算(1) －3＋8－7－15 (2) 23－6×(－3)＋2×(－4)(3)75.04.34353.075.053.1⨯-⨯+⨯- (4)()512423⨯-÷-参考答案：(1) -17 (2) 33 (3) -3.3 (4) -516。

第三讲《有理数》小结与复习一、引学1、有理数：和、和2．数轴：规定了 ___ _ __ 3.相反数：只有、统称有理数。

统称整数；和和的的两个数互为相反数。

统称分数。

叫做数轴。

a 的相反数为4.倒数：；0 的相反数是。

若a、b互为相反数，则有的两个数，称它们互为倒数。

a b ____ 。

数 a(a 0) 的倒数是。

零没有倒数；若a、b 互为倒数，则 ab___5.绝对值：数轴上表示数a的点与的距离叫做绝对值，记作 a 。

一个正数的绝对值是；一个负数的绝对值是它的_ _ _ _；零的绝对值是__。

6．有理数的大小比较：在以右为正方向的数轴上，右侧的点表示的数总比左侧的点表示的数。

两个正数，绝对值较大的数；两个负数比较大小，绝对值大的反而 ______。

7、有理数的运算：包含、、、和运算；混淆运算次序：先算_ _____, 再算 ____ ___, 最后算 __ ____ ，假如有括号，就________ ___. 同级运算从左至右挨次进行。

8. 实数的运算律：加法互换律： ________________________；加法联合律： ________________ ___ ；乘法互换律： ______________ _ ___；乘法联合律： ________________ ___ ；乘法对加法的分派律：__________ ___________ 。

9、科学记数法：把一个大于 1 的数记作的形式（此中1≤a ＜ 10，n为正整数），这类记数方法叫做科学记数法。

二、引思：1、世界上最高的山岳——珠穆朗玛峰，海拔高度为8844.43 米，记作“＋8844.43 ”作。

2、实数 a 、 b 在数轴上对应点的地点如下图，则 ab （填“＞”、“＜”或“＝”）。

3、 －6 的绝对值是（）11 A ． 6 B ．－6 C ．6D ．－64、1的相反数是（）2A. 1B.1 C. 2D.﹣ 2225. 2 的倒数是（ ）A. 1B. 1C. 2D. ﹣ 22 26、在1， 0,1 ，－ 2 这四个数中，最小的数是（） 2 A. 1 B.0C. 1 D.－227、现有以下四个结论：①绝对值等于其自己的有理数只有零；②相反数等于其自己的有理数只有零；③倒数等于其自己的有理数只有1；?④平方等于其自己的有理数只有 1．此中正确的有（ ）A ．0 个B． 1 个 C ． 2 个D．大于 2个8、以下等式建立是 （）A.22B.( 1)1C.1÷( 3)1 2 3 6D.39、衢州市“十二五”规划大纲指出，力求到 2015 年，全市农民人均年纯收入超出13000 元，数 13000 用科学记数法能够表示为（ ）A. 13 103B.1.3 104C.0.13 105D.130 10210、一个纸环链，纸环按红黄绿蓝紫的次序重复摆列，截去此中的一部分，剩下部分如下图，则被截去部分纸环的个数可能是（）（A ）2011（ B ） 2011（C ）2012（D ）2013,,红黄绿蓝紫红黄绿黄绿蓝紫（第 10 题）三、引练：1、计算：⑴． ( 6)( 3)⑵． 8 ( 13)⑶． 8 13⑷． (7) 4 (3) (4) 52、计算⑴． 7( 3)⑵．( 8) ( 13) ⑶． ( 8)(3)75⑷． 481453、计算：⑴．( 7) ( 3) ⑵． ( 7) 3⑶．( 4)( 18) ( 25)⑷． 24 (15 7 )3 6 124、计算：⑴．( 9)( 3) ⑵．( 9) 3⑶． 21 3⑷．1(2)(4)(1)331525、计算：⑴． ( 2)3⑵． ( 3)2⑶． ( 5)2( 1)256、计算：⑴．22(2)(1)⑵． ( 81)9 4 ( 16) 24 9⑶． (21) 1 ( 1) ⑷．( 3)213 223 2 3053四、引伸：1、若| a － 3| － 3＋ a ＝0 , 那么， a 的取值范围是（）A． a ≤3 B ． a ＜3 C ． a ≥3 D ． a ＞32、据相关部门统计， 2010 年一季度，我国城镇新增就业人数为289 万人，用科学记数法表示 289 万正确的选项是（）．．．．A. 2.89 107B. 2.89 106C. 28.9 105D. 289 1042、定义新运算：已知符号 a 表示数字 a 的整数部分，如 4.16 4 ， a 表示数字 a 的小数部分，如 4.16 0.16 。

第一章 有理数 小结与复习一、教学目标：1、理解正负数的意义，掌握有理数的概念和分类；2、借助数轴来理解相反数绝对值，有理数比较大小等知识,解决相关问题。

二、重点难点：重点：求数轴、绝对值、相反数等；难点：与绝对值有关的化简问题。

三、板书设计：第一章 有理数复习课（1） 例3一、正数和负数二、有理数1、有理数的分类2、数轴 例43、相反数4、绝对值5、比较大小四、知识梳理：（速答，快速复习，增强学生对有理数的理解，加深并巩固第一章的内容。

）1.正数和负数（1）定义：大于0的数叫做_____.“+”在正数前面加上符号“-”（负）的数叫做_____.（2）0既不是_____，也不是_____（0还可以表示正数和负数的分界）（3）.可以用正、负数表示具有_____ 的量2、有理数（1）.有理数的概念：_____和_____统称有理数（2）.有理数的分类(a)按定义分类 (b)按符号分类_______________⎧⎧⎫⎪⎪⎬⎨⎭⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩_ _ _ _ _ _ _ _ _有理数　_ _ _ _ __ _ _ _ _ _ _ _ _ _ __________⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩_ _ _ _ _ _ _ _有理数零_ _ _ _ _ _ _ _ （c ）.无限不循坏小数不可化成分数，所以不是有理数，比如_____。

3.数轴(1)定义：可以用一条直线上的点表示数，这条直线叫做_____.(2)数轴的三要素：_____、______、______。

4.相反数（1）定义：只有_____不同的两个数叫做互为相反数（2）规律：正数的相反数是_____，负数的相反数是_____，0的相反数是_____。

（3）若a 、b 互为相反数，则a+b=_____。

（1）数轴上表示数a 的点到原点的距离叫做数a 的_____，记作|a|.（2）一个正数的绝对值是它本身；一个负数的绝对值是它的_____，0的绝对值是0。

七年级上册第1章有理数复习课教案二篇4：《有理数》七年级数学上册教案教学目标【知识与能力目标】掌握有理数的概念，会对有理数按照一定的标准进行分类，培养分类能力。

【过程与方法目标】体验分类是数学上的常用处理问题的方法。

【情感态度价值观目标】要求学生树立勇于探索、积极实践的学习态度，通过合作交流培养协作精神，撰写小论文进一步了解数的发展历史。

教学重难点【教学重点】正确理解有理数的概念。

【教学难点】正确理解分类的标准和按照一定的标准进行分类。

课前准备复习正负数，尝试将之前学过的数进行合理的分类。

教学过程探索新知之前我们已经学习了很多不同类型的数，通过上节课的学习，又知道了现在的数包括了负数，现在请同学们在草稿纸上任意写出3个数(同时请3个同学在黑板上写出)。

问题1：观察黑板上的9个数，并给它们进行分类。

学生思考讨论和交流分类的情况。

学生可能只给出很粗略的分类，如只分为“正数”和“负数”或“零”三类，此时，教师应给予引导和鼓励。

例如：对于数5，可这样问：5和5. 1有相同的类型吗?5可以表示5个人，而5. 1可以表示人数吗?(不可以)所以它们是不同类型的数，数5是正数中整个的数，我们就称它为“正整数”，而5. 1不是整个的数，称为“正分数，。

··…(由于小数可化为分数，以后把小数和分数都称为分数)通过教师的引导、鼓励和不断完善，以及学生自己的概括，最后归纳出我们已经学过的5类不同的数，它们分别是“正整数，零，负整数，正分数，负分数，’。

按照书本的说法，得出“整数”“分数”和“有理数”的概念。

看书了解有理数名称的由来。

“统称”是指“合起来总的名称”的意思。

试一试：按照以上的分类，你能画出一张有理数的分类表吗?你能说出以上有理数的分类是以什么为标准的吗?(是按照整数和分数来划分的)练一练1、任意写出三个有理数，并说出是什么类型的数，与同伴进行交流。

2、教科书第8页练习。

此练习中出现了集合的概念，可向学生作如下的说明。