单回路控制系统整定
- 格式:doc
- 大小:278.50 KB
- 文档页数:11

实验6:气体压力PID单回路控制系统的设计与整定1、测试实验目的1)掌握压力PID单回路控制系统的常用方法。
2)熟悉压力PID单回路控制系统组态。
3)掌握压力PID控制器参数整定方法。
2、实验原理1)压力作用于单位面积上的垂直力,工程上称为压力,物理学中称为压强。
压力依据零点参考压力的不同,分为绝对压力、表压力、压力差、负压力(真空)和真空度。
绝对压力:以完全真空为零标准所表示的压力。
表压力:以大气压为零标准所表示的压力,等于高于大气压力的绝对压力与大气压力之差。
大气压力:一个标准大气压是在纬度45度,温度为0℃,重力加速度为9.80665m/s2海平面上,空气气柱重量所产生的绝对压力,其值是101325Pa。
压差:除大气压力以外的任意两个压力的差值。
负压:绝对压力小于大气压时,大气压力与绝对压力之差为负压。
负压的绝对值称为真空。
真空度:绝对压力小于大气压时的绝对压力。
压力测量常用的单位有:①帕斯卡(Pa),其物理意义是,1牛顿的力作用于1平方米的面积上的压强(力)。
工程中常用MPa表示压力,1 MPa=106 Pa,②工程大气压(kgf/cm2),垂直作用于每平方厘米面积上的力,以公斤数为计量单位。
工程上常用kg/cm2表示。
1 kgf/cm2=9.80665×105 Pa=0.980665 MPa。
③物理大气压(atm),即上面所述的标准大气压。
④毫米汞柱(mmHg)、毫米水柱(mmH2O),垂直作用于底面积上的水银柱或水柱的高度为计量单位。
1 atm=760 mmHg。
许多生产过程都是在不同的压力下进行的,有些需要很高的压力,例如,高压聚乙烯、合成氨生产过程等,有些需要很高的真空度。
压力是化学反应的重要参数,不但影响到反应平衡关系,也影响到反应速率。
生产过程中的其它参数也经常通过压力间接测量,例如,流量、液位、温度等可以转换为压力进行测量。
2)压力的测量压力(压差)的测量方法主要有,液体式、弹性式、活塞式、电动式(电感、电容、电位、应变、压电、霍尔、力平衡、电涡流等)、气动式、光学式(光纤、光干涉、光电、激光等)。




单回路控制系统整定实验报告本文是对单回路控制系统整定实验的总结和分析,主要包括实验目的、实验原理、实验过程、实验结果以及实验分析等方面的内容。
一、实验目的本实验的主要目的是掌握单回路控制系统整定方法,了解控制系统的稳态误差和动态响应特性,提高实际应用控制系统的能力。
二、实验原理单回路控制系统是一种基本的控制系统形式,它由被控对象、传感器、执行机构、控制器和控制信号等组成。
例如,温度控制系统、速度控制系统、压力控制系统等都是单回路控制系统的应用。
在通过控制器使被控对象产生控制输出信号的过程中,存在稳态误差和动态响应特性问题,对其进行整定是控制系统设计中重要的环节。
稳态误差是指控制器输出的控制信号与被控对象实际输出之间的误差。
当被控对象达到稳定状态时,控制器输出的控制信号与被控对象实际输出之间的误差称为稳态误差,在实际控制系统设计中,应尽可能使稳态误差达到最小。
动态响应特性是指控制系统对负载扰动、控制信号变化等外部干扰的响应能力。
在实际应用控制系统中,需要考虑控制系统的动态响应特性,以此保证系统稳定性和控制效果。
控制系统的整定就是调整控制器参数,使系统的稳态误差和动态响应特性达到最优状态,从而获得最佳控制效果。
三、实验过程本实验是基于MATLAB/Simulink软件进行的模拟实验。
实验系统模型:本实验模拟一个简单的单回路负反馈控制系统,其模型如图所示。
其中,控制器采用比例积分控制器(PI控制器),其控制方程为:$$u(t) = K_p e(t) + K_i \int_0^t e(τ) \, dτ$$传感器和被控对象之间的关系用传递函数表示为:$$G(s) = \frac{1}{s(1+0.5s)}$$控制器的参数Kp和Ki需进行整定。
实验过程中,先通过手动调节的方式获得基本的参数范围,再通过曲线法和频率法对其进行精细调整。
曲线法:首先设置一个阶跃参考信号,观察系统的单位阶跃响应曲线,根据曲线特征调整控制器参数。



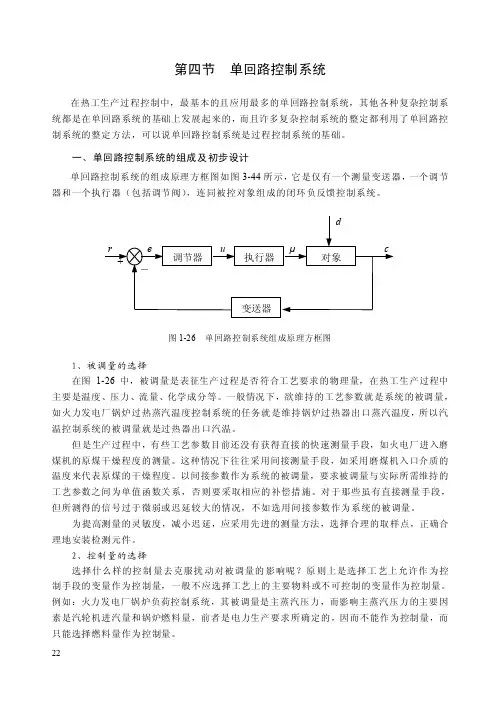
第四节单回路控制系统在热工生产过程控制中,最基本的且应用最多的单回路控制系统,其他各种复杂控制系统都是在单回路系统的基础上发展起来的,而且许多复杂控制系统的整定都利用了单回路控制系统的整定方法,可以说单回路控制系统是过程控制系统的基础。
一、单回路控制系统的组成及初步设计单回路控制系统的组成原理方框图如图3-44所示,它是仅有一个测量变送器,一个调节器和一个执行器(包括调节阀),连同被控对象组成的闭环负反馈控制系统。
图1-26 单回路控制系统组成原理方框图1、被调量的选择在图1-26中,被调量是表征生产过程是否符合工艺要求的物理量,在热工生产过程中主要是温度、压力、流量、化学成分等。
一般情况下,欲维持的工艺参数就是系统的被调量,如火力发电厂锅炉过热蒸汽温度控制系统的任务就是维持锅炉过热器出口蒸汽温度,所以汽温控制系统的被调量就是过热器出口汽温。
但是生产过程中,有些工艺参数目前还没有获得直接的快速测量手段,如火电厂进入磨煤机的原煤干燥程度的测量。
这种情况下往往采用间接测量手段,如采用磨煤机入口介质的温度来代表原煤的干燥程度。
以间接参数作为系统的被调量,要求被调量与实际所需维持的工艺参数之间为单值函数关系,否则要采取相应的补偿措施。
对于那些虽有直接测量手段,但所测得的信号过于微弱或迟延较大的情况,不如选用间接参数作为系统的被调量。
为提高测量的灵敏度,减小迟延,应采用先进的测量方法,选择合理的取样点,正确合理地安装检测元件。
2、控制量的选择选择什么样的控制量去克服扰动对被调量的影响呢?原则上是选择工艺上允许作为控制手段的变量作为控制量,一般不应选择工艺上的主要物料或不可控制的变量作为控制量。
例如:火力发电厂锅炉负荷控制系统,其被调量是主蒸汽压力,而影响主蒸汽压力的主要因素是汽轮机进汽量和锅炉燃料量,前者是电力生产要求所确定的,因而不能作为控制量,而只能选择燃料量作为控制量。
给定值 调节器 对象被调量 - μ 扰动 扰动 图1-28 单回路调节系统 3、控制通道和扰动通道单回路控制系统的组成如图1-27所示,图中W 01(s )为对象的传递函数,它是包括了检测元件、测量变送器、执行机构和调节阀在内的广义对象特性;W c (s )为调节器的传递函数,D 为扰动信号,W 02(s )为被调量与扰动信号间的传递函数。


单回路控制系统实验单回路控制系统概述实验三单容水箱液位定值控制实验实验四双容水箱液位定值控制实验实验五锅炉内胆静(动)态水温定值控制实验实验三实验项目名称:单容液位定值控制系统实验项目性质:综合型实验所属课程名称:过程控制系统实验计划学时:2学时一、实验目的1.了解单容液位定值控制系统的结构与组成。
2.掌握单容液位定值控制系统调节器参数的整定和投运方法。
3.研究调节器相关参数的变化对系统静、动态性能的影响。
4.了解P、PI、PD和PID四种调节器分别对液位控制的作用。
5.掌握同一控制系统采用不同控制方案的实现过程。
二、实验内容和(原理)要求本实验系统结构图和方框图如图3-4所示。
被控量为中水箱(也可采用上水箱或下水箱)的液位高度,实验要求中水箱的液位稳定在给定值。
将压力传感器LT2检测到的中水箱液位信号作为反馈信号,在与给定量比较后的差值通过调节器控制电动调节阀的开度,以达到控制中水箱液位的目的。
为了实现系统在阶跃给定和阶跃扰动作用下的无静差控制,系统的调节器应为PI或PID控制。
三、实验主要仪器设备和材料1.实验对象及控制屏、SA-11挂件一个、计算机一台、万用表一个;2.SA-12挂件一个、RS485/232转换器一个、通讯线一根;3.SA-44挂件一个、CP5611专用网卡及网线、PC/PPI通讯电缆一根。
四、实验方法、步骤及结果测试本实验选择中水箱作为被控对象。
实验之前先将储水箱中贮足水量,然后将阀门F1-1、F1-2、F1-7、F1-11全开,将中水箱出水阀门F1-10开至适当开度,其余阀门均关闭。
具体实验内容与步骤按二种方案分别叙述。
(一)、智能仪表控制1.按照图3-5连接实验系统。
将“LT2中水箱液位”钮子开关拨到“ON”的位置。
图3-4 中水箱单容液位定值控制系统(a)结构图(b)方框图图3-5 智能仪表控制单容液位定值控制实验接线图2.接通总电源空气开关和钥匙开关,打开24V开关电源,给压力变送器上电,按下启动按钮,合上单相Ⅰ、Ⅲ空气开关,给智能仪表及电动调节阀上电。
单回路控制系统参数整定首先,为了实现良好的控制系统性能,我们需要确定四个关键参数:比例增益(Kp),积分时间常数(Ti),微分时间常数(Td)和控制器增益(Kc)。
整定这些参数需要考虑系统的稳态和动态性能。
下面将依次介绍这些参数。
比例增益(Kp)是最基本的一个参数,通过增加或减少输出与输入之间的比例关系来调节系统的响应速度。
当Kp过大时,系统容易产生震荡或不稳定的行为;而Kp过小则会导致系统的响应速度较慢。
Kp的大小一般由试验和经验确定。
积分时间常数(Ti)是对系统的稳态性能进行调节的参数。
增大Ti可以减小系统的稳态误差,但可能会带来较长的调节时间。
根据所需的稳态误差来选择合适的Ti,一般建议取值较大,以避免过度调节。
微分时间常数(Td)用于调节系统的动态响应速度。
增大Td可以减小系统的超调量,但过大的Td可能会导致系统对噪声敏感。
一般来说,选择适当的Td可以使系统具有较好的响应速度和较小的超调量。
控制器增益(Kc)是控制器输出和输入差值的倍数关系。
通过增大或减小Kc来调节控制器的输出量级,从而使控制系统达到预期的性能指标。
一般情况下,Kc的选择需要考虑系统的稳定性和灵敏度。
除了试探法,还有一些优化算法可用于系统参数整定,如:遗传算法、模糊控制和神经网络。
这些算法通过优化目标函数来确定最优的参数值,可以有效减少参数整定的时间和工作量。
然而,这些算法需要较高的计算资源和较长的计算时间,因此在实际应用中需要权衡其效果和成本。
总结起来,单回路控制系统参数整定是实现控制系统性能的关键步骤。
参数整定需要综合考虑系统的稳态和动态性能,并采用适当的方法和技术来确定最优的参数值。
合理的参数整定可以使控制系统达到预期的性能指标,提高系统的稳定性和控制效果。
实验七 SIMULINK 仿真——单回路控制系统及PID 控制器参数整定一、实验目的及要求:1.熟悉SIMULINK 工作环境及特点;2.熟悉控制线性系统仿真常用基本模块的用法;3.掌握SIMULINK 的建模与仿真方法。
二、实验内容:用SIMULINK 建立被控对象的传递函数为11010)(23+++=s s s x G ,系统输入为单位阶跃,采用PID 控制器进行闭环调节。
①练习模块、连线的操作,并将仿真时间定为300 秒,其余用缺省值;②试用稳定边界法(过程控制P5工程整定法之一)设置出合适的PID 参数,得出满意的响应曲线。
③设计M 文件在一个窗口中绘制出系统输入和输出的曲线,并加图解。
三、实验报告要求:①阐述用SIMULINK 进行控制系统仿真的一般过程;②说明用工程整定法——稳定边界法整定PID 参数的过程。
M文件denz=[10];numz=[1 1 10 1];sysz=tf(denz,numz)%传递函数denk=[0 0.539];numk=[0 1];deni=[0 2];numi=[1 0];dend=[0.25 0];numd=[0 1];sysk=tf(denk,numk)%p调节器sysi=tf(deni,numi)%I调节器sysd=tf(dend,numd)%D调节器[denki,numki]=parallel(denk,numk,deni,numi);%P调节器与I调节器相并联[denpid,numpid]=parallel(dend,numd,denki,numki);%PI调节器与D调节器相并联组成PID调节器syspid=tf(denpid,numpid)[denkh,numkh]=series(denpid,numpid,denz,numz);%PID与传递函数串联组成开环控制系统syskh=tf(denkh,numkh)[denbh,numbh]=feedback(denkh,numkh,1,1,-1);%组成单位负反馈闭环系统sysbh=tf(denbh,numbh)t=0:0.1:300;%加入0到300的仿真时间,步进值为0.1subplot(2,1,1)plot(t,1,'b')%显示单位阶跃函数subplot(2,1,2)step(sysbh,t)%显示闭环系统对于单位阶跃函数的响应函数曲线。
单回路控制系统整定
一、实验目的
(1) 掌握动态建模的创建方法。
(2) 掌握单回路控制系统的理论整定方法和工程整定方法。
(3) 了解调节器参数对控制品质的影响。
(4) .熟悉控制线性系统仿真常用基本模块的用法 二、实验仪器
计算机一台、MATLAB 软件 三、实验内容:
用SIMULINK 建立被控对象的传递函数为()
4
1
()101G x s =
+,系统输
入为单位阶跃,采用PID 控制器进行闭环调节。
①练习模块、连线的操作,并将仿真时间定为300 秒,其余用缺省值;
②试用稳定边界法和衰减曲线法设置出合适的PID 参数,得出满意的响应曲线。
③设计M 文件在一个窗口中绘制出系统输入和输出的曲线,并加图解。
四、实验原理
. PID (比例-积分-微分)控制器是目前在实际工程中应用最为广泛的一种控制策略。
PID 算法简单实用,不要求受控对象的精确数学模
型。
.模拟PID 控制器
典型的PID 控制结构如图所示。
. PID 控制规律写成传递函数的形式为
s K s
Ki
K s T s T K s U s E s G d p d i p ++=++==
)11()()()( 式中,P K 为比例系数;i K 为积分系数;d K 为微分系数;i
p i K K T =为积
分时间常数;p
d
d K K T =为微分时间常数;简单来说,PID 控制各校正环节的作用如下:
(1)比例环节:成比例地反映控制系统的偏差信号,偏差一旦产生,
控制器立即产生控制作用,以减少偏差。
(2)积分环节:主要用于消除静差,提高系统的无差度。
积分作用
的强弱取决于积分时间常数i T ,i T 越大,积分作用越弱,反之则越强。
(3)微分环节:反映偏差信号的变化趋势(变化速率),并能在偏差
信号变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减少调节时间。
五、实验步骤
(1)启动计算机,运行MATLAB应用程序。
(2)在MATLAB命令窗口输入Smulink,启动Simulink。
(3)在Simulink库浏览窗口中,单击工具栏中的新建窗口快捷按钮或在Simulink库窗口中选择菜单命令File→New→Modeel,打开一个标题为“Untitled”的空白模型编辑窗口。
(4)用鼠标双击信号源模块库(Source)图标,打开信号源模块库,将光标移动到阶跃信号模块(Step)的图标上,按住鼠标左键,将其拖放到空白模型编辑窗口中。
用鼠标双击附加模块库(Simulink Extra)图标,打开Additional Liner模块库,将光标移动到PID Conttroller图标上,按住鼠标左键,将其拖放到空白模型编辑窗口中。
(5用同样的方法从数学运算模块库(Math Operations)、连续系统模块库(Continuous)和接受模块库(Sinks)中,中把传递函数模块(Transfer Fcn)、示波器模块(Scope)和加法器模块()Sum)拖放到空白模型编辑窗口中。
(6)用鼠标单击一个模块的输出端口并用鼠标拖放到另一模块的输入端口,完成模块间的连接,若需要画支线时,把光标移到有向线段任意点处,按下“Ctrl”键同时按下鼠标左键,拖动鼠标到所需模块。
(7)构造图1所示的单回路反馈系统的仿真模型,其中控制对象由子系统创建,如图2
图1
图2
示,创建子系统的方法是:用鼠标选定待构成子系统的各个模块,包括它们之间的连接线,单击鼠标右键再单击Create Subsystem 即可。
(8)设调节器为比例调节器,对象传递函数为:
0(1)
n
K T s +(其中001,10,4K T n ===),用广义频率特性法按衰减率0.75 计算调节器的
参数;根据 计算结果设置PID 调节器的参数,启动仿真,通过示波器模块观测并记录系统输出的变化曲线。
(9)用响应曲线法整定调节器的参数。
①求出对象的阶跃响应曲线。
②根据响应曲线求取对象的动态特性参数。
③按表1计算调节器的参数,并根据计算结果设置PID 调节器的参数。
④启动仿真,通过示波器模块观测并记录系统输出的变化曲线。
(10)用临界曲线法整定调节器参数。
①先将调节器改成纯比例作用(使,0i d T T =∞=),并将比例增益置于较小的数值,然后将系统投入闭环运行。
启动仿真,通过示波器模块观测并记录系统输出的变化曲线。
逐渐增加比例增益,观测不同比例
增益下的调节过程,直到调节过程出现等幅振荡为止,记录此时的比例带 k δ 和系统的临界振荡周期 k T 。
②根据求得的k δ和k T ,由表2可求得调节器的整定参数。
③将调节器参数设置好,作系统的定值阶跃扰动试验,观测控制过程,并根据响应曲线适当修改整定参数。
(11)用衰减曲线法整定调节器参数。
①先将调节器改成纯比例作用,0i d T T =∞=,并将比例增益置于较小的数值,然后将系统投入闭环运行。
启动仿真,通过示波器模块观测并记录系统输出的变化曲线。
逐渐增加比例增益,观测不同比例②增益下的调节过程,直到调节过程出现衰减率为0.75的振荡为止,记录此时的比例带s δ和系统的临界振荡周期s T 。
由表3可求得调节器的整定参数。
将调节器参数设置好,作系统的定值阶跃扰动试验,观测控制过程,适当修改整定参数,直到控制过程满意为止。
表4-3 临界曲线法整定参数计算表
表4-4 衰减曲线法整定参数计算表
六、实验曲线及数据处理、, 1)临界曲线法
将调节器改成纯比例积分,即i K =0,d K =0。
调整p K 到出现等幅震荡,此时4P K =。
如图3。
图3 由图可知k δ=
1
p
K =0.25,k T =66s 又由临界曲线法整定参数计算表及以下公式关系
1
P k
K δ=
, p i i
K T K =
, d
d P
K T K =
得到调节器的参数:P K =2.4,i K =0.0727,d K =19.8 修改PID 参数得到的曲线图4
图4 (2) 衰减曲线法
将调节器改成纯比例积分,i K =0,d K =0。
调整p K 直到调节过程衰减率为0.75的震荡为止,此时 1.87P K =。
如图5
图5 由图可知1
s P
K δ=
=0.535,s T =78s 由衰减曲线法整定参数计算表及以下公式关系
1
P s
K δ=
, p i i
K T K =
, d
d P
K T K =
得到调节器的参数:p K =2.33, p K =0.09996, i K =18.174 修改PID 参数得到的曲线图
6
图6 七、实验总结
1、P控制规律控制及时但不能消除余差,I控制规律能消除余差但控制不及时且一般不单独使用,D控制规律控制很及时但存在余差且不能单独使用。
2、比例系数越小,过渡过程越平缓,稳态误差越大;反之,过渡过程振荡越激烈,稳态误差越小;若K p过大,则可能导致发散振荡。
T i越大,积分作用越弱,过渡过程越平缓,消除稳态误差越慢;反之,过渡过程振荡越激烈,消除稳态误差越快。
T d越大,微分作用越强,过渡过程趋于稳定,最大偏差越小;但T d过大,则会增加过渡过程的波动程度。
3、。
PID控制器校正后系统响应速度最快,但超调量最大。
学院
过程控制系统实验报告书
实验名称单回路控制系统整定
专业自动化专业
班级
指导教师
姓名
学号
实验日期。