第三章 内压薄壁容器的强度计算(1)
- 格式:pptx
- 大小:228.12 KB
- 文档页数:16




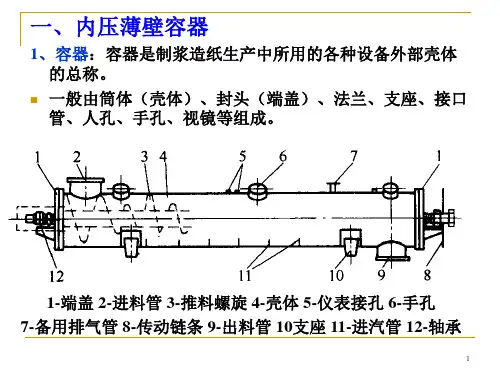

第三章内压薄壁容器设计第一节内压薄壁圆筒设计【学习目标】通过内压圆筒应力分析和应用第一强度理论,推导出内压圆筒壁厚设计公式。
掌握内压圆筒壁厚设计公式,了解边缘应力产生的原因及特性。
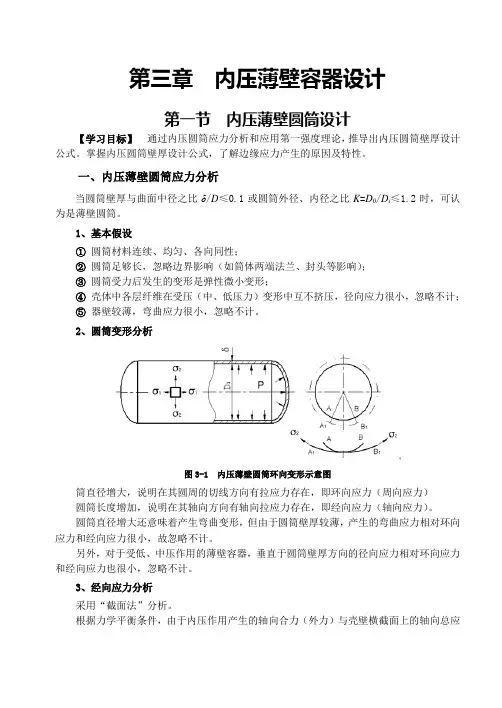
一、内压薄壁圆筒应力分析当圆筒壁厚与曲面中径之比δ/D≤0.1或圆筒外径、内径之比K=D0/D i≤1.2时,可认为是薄壁圆筒。
1、基本假设①圆筒材料连续、均匀、各向同性;②圆筒足够长,忽略边界影响(如筒体两端法兰、封头等影响);③圆筒受力后发生的变形是弹性微小变形;④壳体中各层纤维在受压(中、低压力)变形中互不挤压,径向应力很小,忽略不计;⑤器壁较薄,弯曲应力很小,忽略不计。
2、圆筒变形分析图3-1 内压薄壁圆筒环向变形示意图筒直径增大,说明在其圆周的切线方向有拉应力存在,即环向应力(周向应力)圆筒长度增加,说明在其轴向方向有轴向拉应力存在,即经向应力(轴向应力)。
圆筒直径增大还意味着产生弯曲变形,但由于圆筒壁厚较薄,产生的弯曲应力相对环向应力和经向应力很小,故忽略不计。
另外,对于受低、中压作用的薄壁容器,垂直于圆筒壁厚方向的径向应力相对环向应力和经向应力也很小,忽略不计。
3、经向应力分析采用“截面法”分析。
根据力学平衡条件,由于内压作用产生的轴向合力(外力)与壳壁横截面上的轴向总应力(内力)相等,即:124δσππD p D =由此可得经向应力: δσ41pD=图3-2 圆筒体横向截面受力分析4、环向应力分析 采用“截面法”分析。
图3-3 圆筒体纵向截面受力分析根据力学平衡条件,由于内压作用产生的环向合力(外力)与壳壁纵向截面上的环向总应力(内力)相等,即:22δσL LDp = (3-3)由此可得环向应力: δσ22pD= (3-4) 5、结论通过以上分析可以得到结论:122σσ=,即环向应力是经向应力的2倍。
因此,对于圆筒形内压容器,纵向焊接接头要比环向焊接接头危险程度高。
在圆筒体上开设椭圆形人孔或手孔时,应当将短轴设计在纵向,长轴设计在环向,以减少开孔对壳体强度的影响。


《化工设备机械基础》习题解答第三章 内压薄壁容器的应力分析一、名词解释A 组:⒈薄壁容器:容器的壁厚与其最大截面圆的内径之比小于0.1的容器。
⒉回转壳体:壳体的中间面是直线或平面曲线绕其同平面内的固定轴线旋转360°而成的壳体。
⒊经线:若通过回转轴作一纵截面与壳体曲面相交所得的交线。
⒋薄膜理论:薄膜应力是只有拉压正应力没有弯曲正应力的一种两向应力状态,也称为无力矩理论。
⒌第一曲率半径:中间面上任一点M 处经线的曲率半径。
⒍小位移假设:壳体受力以后,各点位移都远小于壁厚。
⒎区域平衡方程式:计算回转壳体在任意纬线上径向应力的公式。
⒏边缘应力:内压圆筒壁上的弯曲应力及连接边缘区的变形与应力。
⒐边缘应力的自限性:当边缘处的局部材料发生屈服进入塑性变形阶段时,弹性约束开始缓解,原来不同的薄膜变形便趋于协调,边缘应力就自动限制。
二、判断题(对者画√,错着画╳)A 组:1. 下列直立薄壁容器,受均匀气体内压力作用,哪些能用薄膜理论求解壁内应力?哪些不能?(1) 横截面为正六角形的柱壳。
(×)(2) 横截面为圆的轴对称柱壳。
(√)(3) 横截面为椭圆的柱壳。
(×)(4) 横截面为圆的椭球壳。
(√)(5) 横截面为半圆的柱壳。
(×)(6) 横截面为圆的锥形壳。
(√)2. 在承受内压的圆筒形容器上开椭圆孔,应使椭圆的长轴与筒体轴线平行。
(×)3. 薄壁回转壳体中任一点,只要该点的两个曲率半径R R 21=,则该点的两向应力σσθ=m。
(√)4. 因为内压薄壁圆筒的两向应力与壁厚成反比,当材质与介质压力一定时,则壁厚大的容器,壁内的应力总是小于壁厚小的容器。
(×)5. 按无力矩理论求得的应力称为薄膜应力,薄膜应力是沿壁厚均匀分布的。
(√) B 组:1. 卧式圆筒形容器,其内介质压力,只充满液体,因为圆筒内液体静载荷不是沿轴线对称分布的,所以不能用薄膜理论应力公式求解。
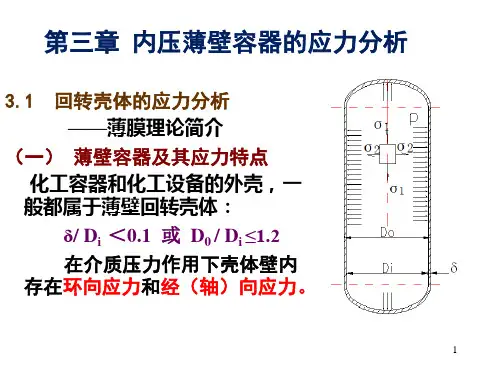
压力容器壁厚计算及说明一、压力容器的概念同时满足以下三个条件的为压力容器,否则为常压容器。
1、最高工作压力P :9.8×104Pa ≤P ≤9.8×106Pa ,不包括液体静压力;2、容积V ≥25L ,且P ×V ≥1960×104L Pa;3、介质:气体,液化气体或最高工作温度高于标准沸点的液体。
二、强度计算公式1、受内压的薄壁圆筒当K=1.1~1.2,压力容器筒体可按薄壁圆筒进行强度计算,认为筒体为二向应力状态,且各受力面应力均匀分布,径向应力σr =0,环向应力σt =PD/4s ,σz = PD/2s ,最大主应力σ1=PD/2s ,根据第一强度理论,筒体壁厚理论计算公式,δ理=PPD -σ][2 考虑实际因素,δ=P PD φ-σ][2+C 式中,δ—圆筒的壁厚(包括壁厚附加量),㎜;D — 圆筒内径,㎜;P — 设计压力,㎜;[σ] — 材料的许用拉应力,值为σs /n ,MPa ;φ— 焊缝系数,0.6~1.0;C — 壁厚附加量,㎜。
2、受内压P 的厚壁圆筒①K >1.2,压力容器筒体按厚壁容器进行强度计算,筒体处于三向应力状态,且各受力面应力非均匀分布(轴向应力除外)。
径向应力σr =--1(222a b Pa 22r b ) 环向应力σθ=+-1(222ab Pa 22r b ) 轴向应力σz =222a b Pa - 式中,a —筒体内半径,㎜;b —筒体外半径,㎜;②承受内压的厚壁圆筒应力最大的危险点在内壁,内壁处三个主应力分别为:σ1=σθ=P K K 1122-+ σ2=σz =P K 112-σ3=σr =-P第一强度理论推导处如下设计公式σ1=P K K 1122-+≤[σ] 由第三强度理论推导出如下设计公式σ1-σ3=P K K 1122-+≤[σ] 由第四强度理论推导出如下设计公式:P K K 132-≤[σ] 式中,K =a/b3、受外压P 的厚壁圆筒径向应力σr =---1(222a b Pb 22r a ) 环向应力σθ=-+-1(222ab Pb 22r a ) 4、一般形状回转壳体的应力计算经向应力 σz =sP 22ρ 环向应力 sP t z =+21ρσρσ 式中,P —内压力,MPa ;ρ1—所求应力点回转体曲面的第一主曲率半径,㎜;(纬)ρ2—所求应力点回转体曲面的第一主曲率半径,㎜;(经)s —壳体壁厚,㎜。
第三章、 3—1内压薄壁壳体强度计算目的要求:使学生掌握内压圆筒内压球形壳体的强度计算,以及各类厚度的相互关系。
重点难点:掌握由第一强度理论推出的内压圆筒,内压球形壳体的强度计算公式。
第三章 内压薄壁容皿本章的任务就是在回转薄壁壳体应力分析的基础上,推导出内压薄壁容皿强度计公式。
本章的压力容皿设计计算公式,各种参数制造要求以及检验标准均与GB150-1998《钢制压力容皿》保持一致。
第一节 压内薄壁壳体强度计算一、 内压圆筒为了保证圆筒受压后不破裂,[根据第一强度理论]应使筒体上最大应力,即环向应力2σ小于等于材料在设计温度下的许用应力[]t σ 用公式表达:2[]2t P D σσδ=≤ ,其中P-设计压力。
1)中径0()2i D D +此外还应考虑到,筒体在焊接的过程中,对焊金属组织的影响以及焊接缺陷(夹渣、气孔、未焊透等)影响缝焊的强度(使整本强度降低),所以将钢板的许用应力乘以一个小于1的焊接接头系数,以弥补焊接可能出现的强度削弱,故2[]2t P D σσδ=≤:[]2t P D σϕδ≤ 此外,工艺计算时通常以i D 做为基本尺寸,故将i D D δ=+代入上式: 则()[]2t i P D δσϕδ+≤ 可解出δ,同时根据GB150-1998规定,确定厚度时的压力用计算压力c p 代替。
最终内压薄壁圆筒体的计算厚度δ:2[]C i t CP D P δσϕ=- 适用:0.4[]t C P σ≤ 考虑到介质时皿壁的腐蚀,确定钢板厚度时,再加上腐蚀裕量: 2C d δδ+=——圆筒的设计厚度再考虑到钢板供货时的厚度偏差,将设计厚度加上厚度负偏差,再向上圆整三规格厚度,这样得到名义厚度。
筒体强度计算公式,除了可以决定承压筒体所需的最小壁厚外,还可用该公式确定设计温度下圆筒的最大允许工作压力,对容皿进行强度校核;可以计算其设计温度下计算应力,判断指定压力下筒体的安全。
例:设计温度下圆筒的最大允用工作压力 由()[]2t i p D δσδ+≤ 推导而来 设计温度下圆筒的计算应力:采用计算压力c p 及i D 代替D ,并考虑焊接头系数ϕ的影响上式变形成: 则设计温度下球壳的厚度计算:考虑腐蚀裕量,设计厚度:再考虑钢板厚度负偏差C 1,再向上图整得到钢板的名义厚度12n C C δδ=+++,同理,确定球壳的最大允许工作压力[Pw],并对其强度进行校核。