下载文档原格式
光子角动量与偏振光子角动量与偏振光子是光的基本粒子，具有能量和动量。
除此之外，光子还具有一种特殊的属性，即角动量。
光子的角动量是指光子围绕其传播方向自旋的动量。
在光学研究中，光子的角动量被广泛应用于光学通信、光学计算、光学操控等领域。
光子角动量的概念最早由爱因斯坦在1905年提出。
他发现，光子的角动量与其偏振状态相关。
偏振是指光波在传播过程中的振动方向。
光波可以是线偏振、圆偏振或椭圆偏振。
不同偏振状态的光波具有不同的角动量。
线偏振光是指光波的电场矢量在一个平面内振动，而在垂直于该平面的方向上没有振动。
对于线偏振光，其角动量大小为0。
圆偏振光是指光波的电场矢量在一个平面内按照圆轨迹旋转。
对于圆偏振光，其角动量大小为ħ（h/2π）。
椭圆偏振光是指光波的电场矢量在一个平面内按照椭圆轨迹旋转。
对于椭圆偏振光，其角动量大小介于0和ħ之间。
光子角动量的大小与其偏振状态有关，但方向与偏振状态无关。
这意味着不同偏振状态的光子具有相同大小的角动量，只是方向不同而已。
这一性质使得光子角动量成为一种重要的信息载体。
利用光子角动量可以实现光学通信中的信息传输和编码。
传统的光学通信系统主要利用光强进行信息传输，但受到信道容量限制。
而利用光子角动量进行信息传输可以大大提高信道容量。
通过调整光子的偏振状态，可以实现多个信息位的编码和传输。
这种技术被称为“空间分割多路复用”，可以同时传输多个独立的信息流。
除了在通信领域，光子角动量还被广泛应用于光学计算和光学操控。
通过调整光子的偏振状态和角动量大小，可以实现对光场的精确控制和操作。
这种技术被称为“光学超分辨率显微镜”，可以实现对微观物体的高分辨率成像。
此外，光子角动量还在量子信息领域发挥着重要作用。
利用光子的偏振状态和角动量可以实现量子比特的编码和传输。
这种技术被称为“量子通信”，可以实现安全和高效的信息传输。
总之，光子角动量与偏振是光学研究中的重要概念。
它们不仅具有理论意义，还具有广泛的应用前景。
光子轨道角动量
光子轨道角动量是光学领域中一个重要的概念，描述了光子在传播过
程中的角动量，是解释和设计光学现象的关键因素。
在光学当中，光子轨道角动量可通过两个重要的物理量来描述：极化
和波前曲率。
极化反映了光子转动的方向，而波前曲率表明了光子旋
转的速度。
光子轨道角动量的研究已经成为了物理学和光学领域中的热门话题，
它不仅有助于我们更深入地理解光学现象，还为我们开发新型的光学
器件提供了奠基之作。
对于光子轨道角动量的研究还有许多问题需要解决。
例如，我们需要
进一步了解在不同波长和极化状况下，光子轨道角动量的变化情况，
以及如何利用这一特性来实现高效率和高精度的光学器件设计和制造。
在未来的研究中，我们需要把握住这一机遇，深入挖掘光子轨道角动
量在光学理论和实践中的作用，并研究新的技术和方法，以期更好地
应用于实际生产和科学发展中。
总之，光子轨道角动量是一个重要的光学概念，对理解和设计光学器件起着关键作用。
通过深入研究光子轨道角动量，我们将探索出更高效和更精密的光学应用，提升光学领域的科研水平，不断推动科学技术的发展进步。
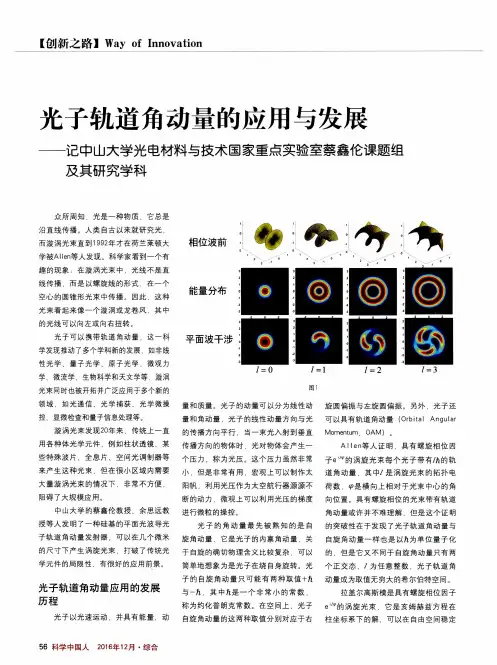
【创新之路】Way of Innovation众所周知，光是一种物质，它总是沿直线传播。
人类自古以来就研究光，而漩涡光束直到1992年才在荷兰莱顿大学被Allen等人发现。
科学家看到一个有趣的现象：在漩涡光束中，光线不是直线传播，而是以螺旋线的形式，在一个空心的圆锥形光束中传播。
因此，这种光束看起来像一个漩涡或龙卷风，其中的光线可以向左或向右扭转。
光子可以携带轨道角动量，这一科学发现推动了多个学科新的发展，如非线性光学、量子光学、原子光学、微观力学、微流学、生物科学和天文学等，漩涡光束同时也被开拓并广泛应用于多个新的领域，如光通信、光学捕获、光学微操控、显微检查和量子信息处理等。
漩涡光束发现20年来，传统上一直用各种体光学元件，例如柱状透镜、某些特殊波片、全息片、空间光调制器等来产生这种光束，但在很小区域内需要大量漩涡光束的情况下，非常不方便，阻碍了大规模应用。
中山大学的蔡鑫伦教授、余思远教授等人发明了一种硅基的平面光波导光子轨道角动量发射器，可以在几个微米的尺寸下产生涡旋光束，打破了传统光学元件的局限性，有很好的应用前景。
光子轨道角动量应用的发展历程光子以光速运动，并具有能量、动量和质量。
光子的动量可以分为线性动量和角动量，光子的线性动量方向与光的传播方向平行，当一束光入射到垂直传播方向的物体时，光对物体会产生一个压力，称为光压。
这个压力虽然非常小，但是非常有用，宏观上可以制作太阳帆，利用光压作为太空航行器源源不断的动力，微观上可以利用光压的梯度进行微粒的操控。
光子的角动量最先被熟知的是自旋角动量，它是光子的内禀角动量，关于自旋的确切物理含义比较复杂，可以简单地想象为是光子在绕自身旋转。
光子的自旋角动量只可能有两种取值+与-，其中是一个非常小的常数，称为约化普朗克常数。
在空间上，光子自旋角动量的这两种取值分别对应于右旋圆偏振与左旋圆偏振。
另外，光子还可以具有轨道角动量（Orbital AngularMomentum, OAM）。
北京航空航天大学课程名称：非线性光学学院：物理科学与核能过程学院姓名：张浩学号：SY1119222光子角动量发展及应用摘要：本文介绍了光子角动量的发展，早在1909年，Poyatmg就认识到光具有角动量—自旋角动量，并将光的角动量与光波的偏振联系起来。
1936年，princeton大学的Beth等人根据四分之一波片可改变圆偏振旋向的性质，利用力学实验巧妙地验证了左、右圆偏振光子分别具有自旋角动量± [4]。
1992年，Leidon大学的Allen等人才认识到了光子也可以携带另一种形式的角动量——轨道角动量。
最后介绍了近年来带有明确角动量的光束高斯一拉盖尔(Laguerre—Gaussian beam，LG光束)光束。
带有角动量的光束可以对微米粒子产生力的作用，进而控制微米粒子。
带有轨道角动量的LG模和像散高斯光束，兼有光学镊子和光学扳手的双重功能。
关键词：角动量，轨道角动量，拉盖尔—高斯1.引言光是非常有趣的，因为我尚未完全地知道它究竟是什么，它的某些属性还令人捉摸不定。
光是什么?这是数百年来人们一直在探索的问题。
1666年，英国物理学家Newton提出了光的微粒说(Corpuscular theory)，把光描绘成为从发光物体发射出来的，作高速运动的一种非常细小的粒子。
1679年，荷兰物理学家Huygens提出了光的波动说，他认为，光是在充满空间的特殊介质“以太”(ether) 中传播的某种弹性波。
Huygens还发现了方解石中光的偏振现象。
但由于Newton 是当时的权威科学家，因此，微粒说一直占上风。
直到1801年，英国物理学家Young做了著名的杨氏双缝干涉实验，1819年法国物理学家Fresnel又用波动理论解释了光的传播和衍射，光的波动说才渐渐为人们所接受。
1861．1862年，英国物理学家Maxwell根据他发现的麦克斯韦方程组大胆预言：光是一种电磁波。
他的预言随后被德国物理学家Hertz的实验所证实。
我国科学家⾸次实现光⼦轨道⾓动量纠缠的量⼦存储
我国科学家⾸次实现光⼦轨道⾓动量纠缠的量⼦存
储
我国科学家在国际上⾸次实现了光⼦轨道⾓动量纠缠的量⼦存储，进⼀步证明了基于⾼维量⼦中继器实现远距离⼤信息量量⼦信息传输的可⾏性。
该研究成果近⽇发表在国际物理学权威期刊《物理评论快报》上。
这是中国科学技术⼤学郭光灿院⼠领导的中科院量⼦信息重点实验室史保森⼩组在⾼维量⼦中继研究⽅向取得的重要进展。
光⼦的轨道⾓动量产⽣于电磁波螺旋前进的波前，可以构成⼀个⽆限维的编码空间。
将光⼦编码在轨道⾓动量空间，可以⼤幅度增加光⼦的信息携带量。
此外，利⽤光⼦的⾼维编码态还可以提⾼量⼦密钥传输的安全性，实现⼆维编码态⽆法完成的量⼦信息协议，并进⾏量⼦⼒学基本问题的研究。
⽽要实现⼤信息量、长距离的量⼦信息传输，必须借助量⼦中继器，⽽量⼦存储单元是构成量⼦中继器的核⼼，因此必须⾸先实现⾼维量⼦纠缠的存储。
史保森教授和博⼠⽣丁冬⽣等继2013年在国际上⾸次实现携带轨道⾓动量的单光⼦存储后，最近他们⼜在该研究⽅向取得重要进展，⾸次实现了光⼦轨道⾓动量纠缠在两个存储单元之间的存储。
他们利⽤两个磁光阱制备了两个冷原⼦团，在其中⼀个冷原⼦团制备了单光⼦与原⼦系综之间的纠缠，然后将该光⼦存储在另⼀个冷原⼦团中，从
⽽实现了轨道⾓动量纠缠在两个原⼦系综之间的存储。
为了检验纠缠特性，他们利⽤量⼦层析技术重构了存储纠缠态的密度矩阵。
通过对⽐存储前后双光⼦⼲涉可视度和计算存储保真度等，来检验存储过程对纠缠程度的影响。
实验结果表明，轨道⾓动量纠缠可以被⾼保真地存储。
第 43 卷第 3 期2024年 5 月Vol.43 No.3May 2024中南民族大学学报（自然科学版）Journal of South-Central Minzu University（Natural Science Edition）石墨烯混合等离子体波导光子轨道角动量产生及转换器设计肖之伟，陈竞翔，江莹，曹振洲*，杨春勇（中南民族大学a.电子信息工程学院；b.智能物联技术湖北省工程研究中心；c.智能无线通信湖北省重点实验室武汉430074）摘要为满足现代社会对通信容量日益增长的需求，设计了一种基于石墨烯混合等离子体波导的可重构光子轨道角动量产生及转换器，利用时域有限差分法对器件的性能进行了仿真分析.仿真结果表明：石墨烯费米能级为0 eV时，该装置实现了拓扑荷由+1向−1或者−1向+1的光子轨道角动量的转换，转换效率达到93.6%；石墨烯费米能级为0.9 eV时，该装置可以将线偏振光转换为携带轨道角动量的涡旋光，此时该器件还可以用于识别拓扑荷为±1的涡旋光.关键词光子轨道角动量；石墨烯；混合等离子体波导；双折射效应；模式耦合中图分类号TN814 文献标志码 A 文章编号1672-4321（2024）03-0378-06doi：10.20056/ki.ZNMDZK.20240312Design of graphene hybrid plasmonic waveguide device for thegeneration and conversion of photonic orbital angular momentum XIAO Zhiwei，CHEN Jingxiang，JIANG Ying，CAO Zhenzhou*，YANG Chunyong（South-Central Minzu University， a.College of Electronics and Information Engineering； b.Hubei Engineering Research Center of Intelligent IOT Technology；c.Hubei Key Laboratory of Intelligent Wireless Communications， Wuhan 430074， China）Abstract A reconfigurable photonic orbital angular momentum generator and converter based on graphene hybrid plasma waveguide was designed to meet the increasing demand for communication capacity in modern society. The performance of the device was simulated by the time-domain finite-difference method. The simulation results showed that when the Fermi level of graphene was 0 eV， the device realized the photonic orbital angular momentum conversion of topological charge from +1 to −1 or −1 to +1 with a conversion efficiency of up to 93.6%. When the Fermi level of graphene was 0.9 eV， the device could convert the linearly polarized light to vortex light carrying orbital angular momentum. In this case， the device can also be used to identify vortex light with topological charge ±1.Keywords photonic orbital angular momentum； graphene； hybrid plasmonic waveguide； birefringence effect； mode coupling当前，视频互联、云计算、大数据等技术广泛应用所产生的海量数据对通信传输容量提出了更高的要求，为此，学者们提出空分复用技术以提升传输容量.空分复用技术与目前应用的偏振复用、波分复用、先进的信号调制格式技术相互兼容，每增加一个空间信道，就能够使现有的通信容量翻倍，实现光通信的持续扩容.王健等［1］实现了携带轨道角动量（Orbital Angular Momentum，OAM）的四束涡旋光复用/解复用，证实了涡旋光通信的可行性.袁小聪等［2］提出了一种基于光纤的OAM（解）复用器，在一个端口直接复用OAM光波，在另一个端口解复用OAM光波，通过对载波信号经过5 km少模光纤传输后的误码率的测量，验证了该方案的有效性，有利于基于OAM大规模光纤通信的应用.余思远等［3］利用环芯光纤中OAM模式的传输和调控特性，实现了多芯OAM光纤系统中纤芯间、纤芯内部模式组信道之间的同时低串扰发射和传输，为光纤通信实现扩容提供了有效的解决方案.光子角动量分为自旋角动量（Spin Angular Momentum，SAM）和轨道角动量，分别与光波的圆偏收稿日期2022-10-04* 通信作者曹振洲（1981-），男，副教授，博士，研究方向：集成光学，E-mail：***********************基金项目国家自然科学基金资助项目（62171487）；中央高校基本科研业务费专项资金资助项目（YZF20001）第 3 期肖之伟，等：石墨烯混合等离子体波导光子轨道角动量产生及转换器设计振态和螺旋相位波前相关.每个光子携带的轨道角动量为l ℏ，其中l 表示拓扑荷［4］.携带轨道角动量的涡旋光模式正交，可避免信道串扰，易于实现模分复用；涡旋光束本征态数目的无穷性，可提高复用通信的维度.光子轨道角动量产生主要有螺旋相位板法［5-6］、模式转换法［7］和计算全息法［8］等.螺旋相位板在模式转换效率以及纯度方面具有较好的效果，但一种螺旋相位板结构只能生成一种OAM 光束，可适用性不强；模式转换法中的柱透镜尺寸相对较大；计算全息法虽能产生任意拓扑荷的涡旋光，但对光栅制作工艺要求严格；空间光调制器可利用编程技术实时改变光束的相位和偏振态，但是其应用于自由空间，无法集成.光子轨道角动量转换主要有超表面［9-10］，其主要应用于自由空间.集成波导具有体积小、损耗低和波导模式稳定等优点［11-12］.蔡鑫伦等［13］提出利用波导产生光子轨道角动量；黄旭光等［14］提出利用波导操纵光子轨道角动量，基于波导模式耦合原理，实现在波导中产生和转换光子轨道角动量.这些方案利用了特定的波导结构调整光波的偏振态和相位分布，灵活性还需要进一步增强.本文设计的基于石墨烯混合等离子体波导的可重构光子轨道角动量产生及转换器，利用一根波导实现光子轨道角动量的产生和转换功能，使器件更紧凑、易于集成，极大地拓展了OAM 在太赫兹通信中的应用.1 器件设计及原理1.1 器件的整体设计及原理设计的基于石墨烯混合等离子体波导的光子轨道角动量产生器如图1所示.该器件由以下部分构成：掺杂硅（Polysilicon ）和高密度聚乙烯（HDPE ）［15-16］共同构成的基底、高密度聚乙烯包层、砷化镓（GaAs ）波导芯、位于高密度聚乙烯介质包层上表面和侧面的石墨烯（Graphene ）.其中，凹槽波导长度L 1=160 µm ，石墨烯总长度L 2=227 µm ，聚乙烯包层的宽度和高度a =30 µm ，砷化镓波导芯的宽度和高度b =22 µm ，石墨烯的宽度c =10 µm ，石墨烯薄层与砷化镓波导之间的间隔s =4 µm .利用FDTD 软件对器件进行仿真，仿真域在各个方向上被划分成相同的立方体，网格间距在各个坐标轴方向（x ，y ，z ）均为0.5 µm ，边界条件选择完美匹配层［17］.该器件的工作波长λ=100 µm ，这是一种用于科学、军事和商业的典型太赫兹波长［18］，如量子级联激光器［19］和超低损耗波导［20］.砷化镓和高密度聚乙烯的材料折射率分别设置为3.6和1.54.石墨烯的费米能级为0.9 eV 时，TM 线偏振光从波导A 端口输入，在波导B 端口输出携带轨道角动量的涡旋光.在波导中，TM 线偏振模式可分解为两个与水平方向夹角为±π/4线偏振光，这两个线偏振光还可以进一步分解为横向电场分量E T 和纵向电场分量E Z ，如图2（a ）所示.横向电场分量E T 与光波的自旋角动量相关.波导中光波的纵向电场分量E Z 指向光波的传播方向，两个纵向电场分量E Z 经过石墨烯混合等离子体波导后相位差达到π/2并在波导输出端口组合形成携带轨道角动量的涡旋光，如图2（b ）所示.1.2 石墨烯混合等离子体波导的设计及功能在太赫兹波段，石墨烯被认为是一个极薄的导电层，与单层石墨烯表面等离子体的传播特性相比，少数层石墨烯对表面模式的约束较弱，传播损耗较小［21］.本文该器件使用了几层石墨烯构造石墨烯混合等离子体波导.在随机相位近似的条件下，根据Kubo 公式［22］，单层石墨烯的表面电导率为：图 1 石墨烯混合等离子体波导的光子角动量产生及转换器Fig.1 Graphene hybrid plasmonic waveguide device for generationand conversion of photonic angular momentum图 2 波导的模场分布Fig.2 Field distribution of waveguide379第 43 卷中南民族大学学报（自然科学版）σg(ω，τ，T，E f)=2ie2k B Tπℏ(ω+iτ-1)ln[2cosh(E f2k B T)]+ e24ℏ[12+1πarctan(ℏω-2E f2k B T)]- i2πln[(ℏω+2E f)2(ℏω-2E f)2+(2k B T)2]，（1）式中：ℏ为简化后的普朗克常数，ω为角频率，k B为波尔兹曼常数，室温T=300 K，载流子弛豫时间τ=0.5 ps，石墨烯的费米能级可由E f=ℏυf(πn g)1/2（υf为费米速度，n g为载流子浓度）确定.少数层石墨烯可以看作是若干层没有相互作用的单层石墨烯的叠加，其电导率可以表示为Nσg·当石墨烯的层数N<6层时，随着石墨烯层数的增加，石墨烯附近的光波损耗逐渐下降［23］，在器件仿真过程中，设置石墨烯的层数N=5.设计的石墨烯混合等离子体波导结构如图3所示，该结构包含多种电介质：砷化镓波导、高密度聚乙烯包层和高密度聚乙烯包层上面和侧面的石墨烯，具有限制、传输和耦合电磁波的功能［24］.石墨烯混合等离子体波导支持两个本征模式E-Mode1和E-Mode2的传输.电磁波的能量集中于介质波导内部（E-Mode2）或介质波导与石墨烯的间隙中（E-Mode1）.在波导输入端口部分，光波模式有效折射率为2.45，当石墨烯的费米能级为0.9 eV时，光波经过石墨烯混合等离子体波导，两个波导模式的光场分布存在较大差异，两个模式的有效折射率实部差值Δn 可以表示为：⁃Δn=|Ren E⁃Mode1-Ren E⁃Mode2|，（2）此时石墨烯混合等离子体波导的两个本征模式E-Mode1模式和E-Mode2模式的有效折射率n E⁃Mode1= 2.57+0.0026i和n E⁃Mode2=2.46+0.0004i，实部表示了模式有效折射率，虚部代表了波导结构的损耗.两个模式的有效折射率实部之差为0.11，有效折射率实部差异引起两个本征模式产生相位差δ［25］：δ=k0ΔnL+Δδ，（3）式中：k0为自由空间中波矢量（k0=2π/λ，λ为器件工作波长），Δn为两个波导模式有效折射率实部的差值，L为本节设计的石墨烯混合波导长度和下节设计的凹槽波导长度，Δδ为波导模式的初始相位差.用公式（3）计算可知：石墨烯混合等离子体波导长度L2=227 µm时，光波经过石墨烯混合等离子体波导到达输出波导端口，两个纵向场分量E Z的相位差达到δ=π/2，组合形成携带轨道角动量的涡旋光. 1.3 凹槽波导的设计及功能设计的凹槽波导结构如图4所示，凹槽波导支持TM模式和TE模式的传输.随着光波的传输，两个模式的相位产生差异，形成双折射效应.凹槽波导中TM模式有效折射率、TE模式有效折射率和两个模式之间的相位差δ随波导宽度的变化关系如图5所示.由图5可见：随着波导宽度的增加，两个模式之间的有效折射率之间的差值越来越小，相对相位差也在减小.凹槽波导宽度为W=17 µm时，TM模式和TE模式的有效折射率实部n TM=2.27，n TE=1.93，两者之差为0.34.凹槽波导长度L1=160 µm时，光波经过凹槽波导后，由公式（3）可知TE模式和TM模式的相位差达到π.涡旋光经过凹槽波导的相移作用后，转换为相反旋向的涡旋光，实现拓扑荷为+1向-1或者-1向+1的光子轨道角动量的转换.当波导宽度为22 µm时（没有凹槽），波导的TE模式和TM模式相等，该波导没有相移功能，不能实现涡旋光的转换功能.图5 TM模式和TE模式的有效折射率和相位差随凹槽波导宽度W的变化关系Fig.5 Variation of effective index and phase difference withthe width W of groove waveguide under TM and TE modes图3 石墨烯混合等离子体波导结构示意图Fig.3 Schematic diagram of graphene hybrid plasmonicwaveguide structure图4 凹槽波导结构示意图Fig. 4 Schematic diagram of groove waveguide structure380第 3 期肖之伟，等：石墨烯混合等离子体波导光子轨道角动量产生及转换器设计2 器件的优化与性能分析两个模式的重叠积分Overlap 为［26］：Overlap =|||||||||Re éëêêêêùûúúúú()∫E 1×H ∗2⋅dS ()∫E 2×H ∗1⋅dS ()∫E1×H ∗1⋅dS ×|||||1Re (∫E 2×H ∗2⋅dS ) ，（4）式中，E和H 分别为在波导中光波的电场和磁场强度.当输入波导的宽度为22 µm 时，由公式（3）和（4）计算得到凹槽波导长度随着凹槽波导的宽度W 的变化关系，以及输入波导TM 模式与凹槽波导TM 模式的重叠积分Overlap 随着凹槽波导的宽度W 的变化关系，如图6所示.由1.3分析可知凹槽波导宽度为10~20 µm 时，随着凹槽波导宽度的增加，凹槽波导支撑的TE 模式和TM 模式的有效折射率差Δn 随之减小.依据公式（3）可知：Δn 减小时，通过增加凹槽波导的长度L 1可以使凹槽波导支撑的TE 模式和TM 模式的相位差δ差达到π.同时，两个模式的重叠积分也在逐渐增大.当凹槽波导宽度为22 µm 时，两个模式的重叠积分为1，但此时凹槽波导没有相移功能，不能对拓扑荷±1的涡旋光进行转换，所以凹槽波导的宽度需小于输入波导的宽度.当凹槽波导宽度为18~21 µm 时，由公式（3）算得凹槽波导的长度超过200 µm ，不利于集成. 当凹槽波导宽度为17 µm 时，本征模式与输入模式重叠积分为0.997，表明输入TM 模式的能量几乎全部被转移给了凹槽波导的TM 模式，此时的凹槽波导结构有利于TM 线偏振光的传输，凹槽波导长度约为160 µm ，易于集成.光子轨道角动量转换器的转换效率η是衡量器件性能的重要指标，其计算公式为：η=P outputP input×100% ，（5）式中：P input 为波导A 端口的光波输入功率，P output 为波导B 端口的光波输出功率.光子轨道角动量产生器的输出端口光波转换效率η随石墨烯费米能级的变化关系如图7所示，石墨烯费米能级分别为0.2、0.6、0.9 eV 时波导输出端口的光波的模场分布有明显不同，对应涡旋光转换效率分别为12.3%、83.8%、93.6%.由图7可知：随着石墨烯费米能级的增加，涡旋光的模场更接近圆形分布，涡旋光的转换效率η也在逐渐提高.波导模式的损耗随石墨烯费米能级的变化关系如图8所示.由图8可见：石墨烯的费米能级为0.2~0.9 eV 时，石墨烯混合等离子体波导中E -Mode1和E -Mode2模式损耗随石墨烯费米能的增加而减小， 耗变化也越来越缓慢.石墨烯的费米能级为0.2 eV 时，E -Mode1、E -Mode2损耗分别为38.11、2.16 dB‧mm -1，两个模式基本被吸收；石墨烯费米能级为0.9 eV 时，E -Mode1和E -Mode2损耗分别为1.46、0.22 dB‧mm -1，此时石墨烯混合等离子体波导结构中传输模式的损耗非常小，有利图7 波导输出端口模场分布和转换效率η随石墨烯费米能级的变化关系Fig.7 Variation of mode field distribution and conversion efficiency ηof the waveguide output port with the Fermi level of graphene图8 波导两个本征模的传播损耗随石墨烯费米能级的变化关系Fig.8 Variation of propagation losses of the two eigenmodes of thewaveguide with the Fermi level of graphene图6 波导长度和波导模式的重叠积分随波导宽度的变化关系Fig. 6 Variation of waveguide length and overlap integral forwaveguide modes with waveguide width381第 43 卷中南民族大学学报（自然科学版）于光子轨道角动量的产生和转换.另外，通过调节石墨烯费米能级可以补偿部分工艺问题导致的材料属性或者结构尺寸的偏差对波导产生的影响.在仿真中设置合适的石墨烯宽度c ，调节波导间隔s ，使得器件的转换效率达到最大值，不同石墨烯宽度c 对应的波导间隔s 与转换效率η间的关系如图9所示.由仿真结果可知：当波导间隔s 大于4 µm 时，器件转换效率随波导间隔s 变化不明显；波导间隔在1.5~6.5 µm 范围时，OAM 模式转换效率均高于60%；当石墨烯层的宽度为10 µm ，波导间隔s 为5.5 µm 时，器件的转换效率达到了93.9%，为最大值；s 为4 µm 时，对应的OAM 模式转换效率为93.6%.当波导间隔小于1.5 µm 时不利于生成涡旋光；波导间隔s 大于6.5 µm 时，石墨烯混合波导的两个本征模式有效折射率差Δn 较小，依据公式（3）可知，需要增加石墨烯混合波导的长度L 2使两个模式的相位差δ达到π/2，此时波导的长度超过800 µm ，不利于集成；s =5.5 µm 时，TM 模式转换为OAM 模式所需的波导长度为431 µm ；当s =4 µm 时，TM 模式转换为OAM 模式所需的波导长度为227 µm ，此时器件的尺寸更小，更有利于集成，最终设置波导间隔s 为4 µm ，石墨烯层的宽度c =10 µm .3 涡旋光的拓扑荷识别和转换功能石墨烯混合等离子体波导可将线偏振光转换为涡旋光，由光的互易性，涡旋光也可以转化为线偏振光.该波导装置还可以识别拓扑荷为±1的涡旋光.如图10（a ）所示，当石墨烯能级为0.9 eV 时，右旋涡旋光从波导B 端口输入，在波导A 端口输出TE 线偏振光；由图10（b ）可知，左旋涡旋光从波导B 端口输入，在波导A 端口输出TM 线偏振光.涡旋光可以看作由两个相互正交、振幅相同、初始相位差Δδ=±π/2的线偏振光组成，涡旋光经过石墨烯混合等离子体波导结构后两个相互正交的线偏振光的初始相位差会产生π/2的积累.依据公式（3）可知，当拓扑荷l =1的右旋涡旋光经过波导结构后，线偏振光之间的相位差达到0，组合形成了TE 线偏振光；当拓扑荷l =-1的左旋涡旋光经过波导结构后，相位差达到π，组合形成了TM 线偏振光.图11为拓扑荷为±1的涡旋光转换器示意图.当石墨烯的费米能级为0 eV 的时，波导结构几乎不会改变光波的偏振态和螺旋波阵面，此时利用凹槽波导的相移作用进行不同旋向的涡旋光转换，从波导端口输入涡旋光，在波导输出端口产生与其相反旋向的涡旋光，即当右（左）旋涡旋光从波导A 端口输入，就会从波导B 端口输出左（右）旋涡旋光.图9 不同石墨烯层宽度c 对应的波导间隔s 与转换效率的关系Fig.9 Relationship between of conversion efficiency and waveguideinterval s with different graphene layers widthc图11 拓扑荷为±1的涡旋光转换器示意图Fig.11 Schematic diagram of vortex light converter withtopological charge±1图10 拓扑荷为±1的涡旋光区分器示意图Fig.10 Schematic diagram of a vortex discriminator withtopological charge ±1382第 3 期肖之伟，等：石墨烯混合等离子体波导光子轨道角动量产生及转换器设计4 结语本文设计并数值仿真了一种基于石墨烯混合等离子体波导的可重构光子轨道角动量产生及转换器，当石墨烯费米能级为0.9 eV时，石墨烯混合等离子体波导的两个本征模式纵向场分量E Z的相位差达到π/2并组合形成携带轨道角动量的涡旋光，转换效率达到93.6%，同时该器件可以区分拓扑荷为±1的涡旋光；当石墨烯费米能级为0 eV时，涡旋光从波导端口输入，经过凹槽波导的相移作用，两个本征模式组合形成了相反旋向的涡旋光，实现了拓扑荷为+1向-1或者-1向+1的光子轨道角动量的转换.该装置相比已有的硅基波导光子轨道角动量产生器，结构更为紧凑、功能更为灵活，可用于片上模式转换.参考文献［1］WANG J，YANG J Y，FAZAL I M，et al. Terabit free-space data transmission employing orbital angular momentummultiplexing［J］. Nature Photonics， 2012， 6（7）： 488-496.［2］XIE Z， GAO S， LEI T， et al. Integrated （de）multiplexer for orbital angular monmentum fiber communication［J］.Photonics Research， 2018， 6（7）： 743-749.［3］LIU J，ZHANG J ，LIU J，et al. 1-Pbps orbital angular momentum fibre optic transmission［J］. Light：Science &Applications， 2022， 11（1）： 1-11.［4］杨春勇，闪开鸽.基于卷积神经网络的涡旋光相干解复用［J］.中南民族大学学报（自然科学版）， 2020， 39（4）：390-396.［5］BEIJERSBERGEN M W，COERWINKEL R P C，KRISTENSEN M，et al. Helical-wavefront laser beamsproduced with a spiral phase plate［J］. Optics Communications，1994， 112（5/6）： 321-327.［6］ZHOU J， LIN P T. Efficient mid-Infrared vortex beam generation using optical waveguides integrated with micro-spiral phase plates［J］. Journal of Optics， 2019， 21（10）： 105801.［7］侯金，王林枝，杨春勇，等.轨道角动量通信研究进展［J］.中南民族大学学报（自然科学版）， 2014， 33（1）： 67-72.［8］MAIR A， VAZIRI A， WEIHS G， et al. Entanglement of the orbital angular momentum states of photons［J］. Nature，2001， 412（6844）： 313-316.［9］ZHUO L，LONG W，JIANG M，et al. Graphene-based tunable Imbert-Fedorov shifts and orbital angular momentumsidebands for reflected vortex beams in the terahertzregion［J］. Optics Letters， 2018， 43（12）：2823-2826.［10］ZHU W，GUAN H，LU H，et al. Orbital angular momentum sidebands of vortex beams transmitted througha thin metamaterial slab［J］. Optics Express， 2018， 26（13）：17378-17387.［11］侯金，李博雅，王林枝，等. 硅基宽带双偏振单模狭缝波导（英文）［J］. 中南民族大学学报（自然科学版）， 2015，34（1）： 79-82.［12］LEE I J，KIM S. Directional coupler design for orbital angular momentum mode-based photonic integratedcircuits［J］. Optics Express， 2020， 28（20）： 30085-30093.［13］LI S， DING Y， GUAN X， et al. Compact high-efficiency vortex beam emitter based on a silicon photonics micro-ring［J］. Optics Letters， 2018， 43（6）： 1319-1322.［14］NI F C，XIE Z T，HU X ，et al. Selective angular momentum gennerator based on a graphene hybrid plasmonicwaveguide［J］. Journal of Lightwave Technology， 2019，37（21）： 5486-5492.［15］MEI J，ZHONG K，XU J，et al. Efficient terahertz generation via GaAs hybrid ridge waveguide［J］. IEEEPhotonics Technology Letters， 2019， 31（20）： 1666-1669.［16］SOMMER S，RAIDT T，FISCHER B M，et al. THz-spectroscopy on high density polyethylene with differentcrystallinity［J］. Journal of Infrared，Millimeter andTerahertz Waves， 2016， 37（2）： 189-197.［17］BERENGER J P. A perfectly matched layer for the absorbtion of electromagnetic waves［J］. Journal ofComputational Physics， 1994， 114（2）： 185-200.［18］NORDQUIST C D， WANKE M C， ROWEN A M， et al.Properties of surface metal micromachined rectangularwaveguide operating near 3 THz［J］. IEEE Journal ofSelected Topics in Quantum Electronics， 2011， 17（1）：130-137.［19］WU C，KHANAL S，RENO J L，et al. Terahertz plasmonic laser radiating in an ultra-narrow beam［J］.Optica， 2016， 3（7）： 734-740.［20］HE X， NING T， LU S， et al. Ultralow loss graphene-based hybrid plasmonic waveguide with deep-subwavelengthconfinement［J］. O ptics E xpress，2018，26（8）：10109-10118.［21］GAN C H. Analysis of surface plasmon excitation at terahertz frequencies with highly doped graphene sheetsvia attenuated total reflection［J］. Applied PhysicsLetters， 2012， 101（11）： 847-612.［22］CHEN P Y， ALU A. Atomically thin surface cloak using graphene m onolayers［J］. A CS N ano，2011，5（7）：5855-5863.［23］CASIRAGHI C， HARTSCHUH A， LIDORIKIS E， et al.Rayleigh imaging of graphene and graphene layers［J］.Nano Letters， 2007， 7（9）： 2711-2717.［24］陆梦佳，王跃科，姚志飞，等.基于一维随机硅光栅的石墨烯表面等离子体安德森局域［J］.光子学报，2019， 48（4）： 35-41.［25］JIN L，CHEN Q，WEN L. Mode-coupling polarization rotator based on plasmonic waveguide［J］. Optics Letters，2014， 39（9）： 2798-2801.［26］BAI X，CHEN H，CAO H. Generation of higher-order orbital angular momentum modes and （de）multiplexingbased on double-trench SOI waveguide［J］. Journal ofModern Optics， 2022， 69（2）： 60-71.（责编&校对 刘钊）383。
奇异光场中光子角动量的研究二、报告正文（一）项目的立项依据与研究内容1、项目的立项依据光子角动量是光波中除了强度、相位和偏振以外的另一重要特性。
虽然不是任意光束都会存在角动量，但其具有十分重要的研究和应用意义。
近年来，对于光子角动量的研究和应用成为光学的许多领域中前沿，例如：量子光学[1,2,8]，纳米光学[3,4]，衍射光学[5,6]，非线性光学[7]等。
与经典力学相同，光子角动量被表达为r×p，其中r为光子相对参考点的位置，p为光子线动量，被定义为p=ε0E×B，ε0为电介质常数，E和B分别为电场和磁场振幅。
可以看出只有在沿轴向具有电场或磁场分布的光场可以存在角动量。
因此，对于理想情况下的平面光波场中不可能存在角动量。
但在实际光束的产生和传播过程中，电磁场在受到自身尺寸或光学器件等光瞳的影响，形成沿轴向的分量，从而具有角动量。
因此光子角动量广泛存在于光场中。
光子角动量可分为两种类型：自旋角动量和轨道角动量。
前者指光子微扰自身旋转形成的角动量；后者指光子在传输过程中围绕光轴旋转。
针对这两种角动量，两种典型的光束引起的角动量得到了大量的研究：圆偏振光束中的光子自旋角动量；具有螺旋相位结构的涡旋光束中的轨道角动量。
1909年，Poynting首次提出在圆偏振光场中存在以ħ为单位的角动量11，随后被Beth实验上通过圆偏振光旋转双折射物体证实12。
自旋角动量存在较简单的两种值+ħ或-ħ，取决于圆偏振光的旋转方向。
因此人们针对这种角动量的基础研究基本停止。
但对光子自旋角动量的应用研究取得了巨大的进展。
除了利用其进行光操控技术外13 14，圆偏振光可以利用光子自旋角动量与自旋材料相互作用控制磁序材料中电子的自旋15。
2012年，Heinz课题组在二硫化钼单层材料上利用圆偏振光开创了对valley自由度（valleytronics）的控制的可能性16。
光子轨道角动量真正引起人们注意是在1992年，Allen等理论上预言了具有螺旋相位的光场可以产生以ħ为单位的角动量，并且该角动量可以在实验上实现7。
与自旋角动量不同，轨道角动量由于取决于光波场中螺旋相位的拓扑荷值，光子可以携带的轨道角动量没有理论上限，即可以远远大于ħ，例如Fickler利用计算全息技术实现了300ħ的轨道角动量1。
实验上实现这种很大的光子轨道角动量在过去的十年中对轨道角动量的应用得到了巨大的发展9。
光子轨道角动量由于可以具有较大的值从而在操控微粒时产生较大的扭矩，被大量应用于光镊技术中6，21。
Wang等2011年将光子轨道角动量作为一个新的自由度应用与光通信中，通过对轨道角动量的波分复用实现了自由空间中兆兆比特的数据传输17，18。
欧洲物理学会的物理世界（）揭露了2012年的十大物理突破之一是：缠绕扭曲光束，即利用轨道角动量形成缠绕光子对的新技术实现了对300对缠绕光子的操控19，是以前缠绕光子对的十倍以上。
这种角动量的量子缠绕可以被用于量子通讯、量子计算等。
更有趣的是，携带有轨道角动量的光束可以用于特殊形貌的微纳加工20、大气通信22和天体研究23等领域。
虽然形成这两种角动量的机制不同，但在特定光场中，二者可以相互转化。
例如圆偏振光经过特殊衍射元件24，或被强聚焦25后均可以实现自旋和轨道角动量之间的互相转换。
这两种角动量之间的转化可以为量子通信、光学操控等提供更多的自由度。
从上述光子角动量的研究进展可以看出人们对其的基础和应用研究在过去的两年内得到了迅猛发展。
可以预计在未来的五到十年内将会成为光学领域的研究热点，同时相关研究可以应用到任意其它自然界中存在的波动系统中（包括微波28、物质波29、电子波27等）。
迄今为止，国际上许多小组都开展了光子角动量方面的研究，包括美国的普林斯顿大学、加州理工、康奈尔大学、旧金山州立大学，以色列的以色列理工大学，澳洲的澳大利亚国家大学，英国圣安德鲁斯大学等。
在国内，南开大学的王慧田教授和袁晓聪教授课题组分别对角动量在微纳尺度展开了十分深入的研究，并开展了光操控应用26,26a,26b；南京大学固体微结构物理国家重点实验室针对金属等离子体艾里光束进行了实验研究16；浙江大学的赵道木教授和华南师范大学的郭旗教授对艾里光束进行了大量的理论研究。
本项目主要根据课题组前期对一些新型奇异光场的研究基础上提出对奇异光场中光子角动量的进一步深入研究。
奇异光场是指光场的相位或偏振等存在无法定义或无穷大的奇异点，例如涡旋光束30、柱对称矢量光束31、艾里光束32、贝塞尔光束33,33a等。
光场中的奇点引入了不均匀的偏振态和相位分布，导致一些新的效应和现象。
光子角动量便是这些效应中的典型结果。
在不均匀的偏振或相位分布下，光场在传输过程中其线动量出现沿轴向的分量，对应了角动量的形成。
涡旋光束由于其螺旋相位结构而存在轨道角动量已经得到充分认识，并得到大量的研究9。
本课题组最近对于柱对称矢量光束和艾里光束等一系列奇异光束通过掩模板遮挡、强聚焦等方法实现了复杂轨道和自旋角动量分布的产生和调控34。
虽然这些奇异光场中可能存在角动量，但要对其进行应用并发展为比较成熟的技术仍存在需要解决的问题，包括如何对其进行准确测量以及对其产生和调控。
正如上面所提到的，早在1992年轨道角动量被提出时便已经被证实了其值与光学涡旋的拓扑荷m有关，且具有特定的比例关系。
但在实际工程中所形成涡旋光场的拓扑荷值不一定准确，且由于轨道角动量与能流密度也有关系，但光强分布不均匀时，其值不能利用拓扑荷直接得到。
最近，对于光学涡旋轨道角动量的实验测量，Padgett等人利用棱镜结合干涉光路得到了较好的结果35。
同时山东师范大学的国承山小组利用傅里叶变换有效测得了角动量与拓扑荷之间的比例关系36。
但是，对于其它非涡旋光场的角动量如何测量仍未得到解决。
而轨道角动量虽然很多光场中均存在，但只能取较为离散值，不适合于实际应用，同时这些光场在实验上通常只能利用激光器的输出模式或利用效率较低的腔外被动方法产生。
因此，为利用轨道角动量仍需解决所产生的光场具有任意取值的轨道角动量且该值容易调节，同时光场要具有较高的效率。
而对于存在与偏振奇异光场中的与偏振有关的光子自旋角动量的测量仍然没有得到有效解决。
南开大学王慧田教授利用光场与微粒的相互作用，通过观察其中微粒的运动实现了角动量的测量26。
奇异光场由于角动量的存在而在传输过程中存在一系列特殊的演化特性。
例如具有相位奇点的涡旋光束在线性介质中，光场中当其强度分布沿相位梯度方向分布不均匀时由光电角动量驱动的旋转光波能流使其强度分布发生明显改变，同时光场的轨道角动量会发生相应改变。
例如对于非中心对称的涡旋光场，其在传输过程中整个光场会发生旋转37。
而对于具有多个相位奇点的光场，其轨道角动量也会随着多个涡旋之间的相互作用而发生改变38。
这些轨道角动量的演化均呈现出较为迷人的特性，但光场在传输过程中这种角动量的变化无法得到有效测量。
另外，柱对称矢量光束在线性传输过程中，经过强聚焦、散射或反射后均可以表现自旋和轨道角动量之间的相互转换34。
在非线性光学中，光子与非线性介质相互作用丰富了角动量的演化特性。
在自聚焦非线性介质中，轨道角动量使涡旋光束受到强烈的方位角调制非稳从而形成一系列具有角动量的亮斑39。
相似地，携带有自旋角动量的柱对称矢量光束在Kerr自聚焦介质中也会坍塌为多个亮斑40。
这种奇异光束的演化过程虽然可以利用其光强分布来表示，但是角动量的作用以及其演化过程没有引起重视。
事实上，测量光子演化的角动量，可以从更深层次来理解光子与物质作用机制。
另外，轨道角动量与非线性周期波导阵列的相互作用也引起了广泛关注。
当非线性与周期势场对角动量的调制可以达到平衡时，角动量可以保持稳定并支持孤波态41。
否则，光子与周期波导间发生直接角动量的转换42。
因此，研究奇异光场与非线性介质的相互作用可以为产生和调控光子角动量提供一种有效手段。
本项目涉及的另一类特殊光束是在2012年提出并成为研究热点的非傍轴自弯曲无衍射光束43。
这类光束虽然是严格按照麦克斯韦方程求解得到，不存在奇异点。
但是与麦克斯韦方程的普通解，例如高斯光束相比，这种光束存在许多奇异特性。
例如非傍轴无衍射光束可以沿圆形、椭圆或抛物线轨道传输，而这个过程不需要非线性等作用来保持。
这对于提高光学传感器效率、光线绕过障碍物以及弯曲表面的加工都存在巨大的潜在应用。
本课题组最近实现了柱对称非傍轴无衍射光束，这种光束具有较强的相位梯度同时可以具有复杂的偏振态分布，从而为角动量的产生和调控提供新的思路。
[1] J. Durnin, J. J. Miceli Jr., and J. H. Eberly, Diffraction free beams, Phys. Rev. Lett. 58, 1499(1987).[2] R. Fickler, R. Lapkiewicz, W. N. Plick, M. Krenn, C. Schaeff, S. Ramelow, and A. Zeilinger,Quantum Entanglement of High Angular Momenta, Science338, 640–643 (2012).[3] J. Wang, J. Y. Yang, I. M. Fazal, N. Ahmed, Y. Yan, H. Huang, Y. X. Ren, Y. Yang, S.Dolinar, M. Tur, and A. E. Willner, Terabit free-space data transmission employing orbital angular momentum multiplexing, Nature Photonics 6, 488–496 (2012).[4] M. N. Litchinitser, Structured light meets structured matter, Science337, 1054–1055(2012).[5] X. Cai, J. Wang, M. J. Strain, B. J. Morris, J. Zhu, M. Sorel, and J. L. O’Brien,. Integratedcompact optical vortex beam emitters, Science338, 363(2012).[6] N. Yu, P. Genevet, M. A. Kats, F. Aieta, J. P. Tetienne, F. Capasso, and Z. Gaburro, Lightpropagation with phase discontinuities: generalized laws of reflection and refraction, Science334, 333–7 (2011).[7] M. Padgett, and R. Bowman, Tweezers with a twist.,Nature Photonics 5, 343–348 (2011).[8] L. Allen, M. W. Beijersbergen, R. J. C. Spreeuw, and J. P. Woerd- man, Orbitalangular-momentum of light and the transformation of Laguerre–Gaussian laser modes, Phys. Rev. A45, 8185–8189 (1992).[9] G. M. Terriza, P. Juan, and T. L.Torner, Twisted photons, Nature Physics 3, 305–310(2007).[10] A. M. Yao, and M. J. Padgett, Orbital angular momentum: origins, behavior andapplications., Advances in Optics and Photonics3, 161(2011).[11] J. Poynting, The wave motion of a revolving shaft, and a suggestion as to the angularmomentum in a beam of circularly polarised light, Proc. R. Soc. Lond. A Ser. A82, 560–567 (1909).[12] R. Beth, Mechanical detection and measurement of the angular momen- tum of light, Phys.Rev. 50, 115–125 (1936).[13] A. T. O. Neil, I. Macvicar, L. Allen, and M. J. Padgett, Intrinsic and Extrinsic Nature of theOrbital Angular Momentum of a Light Beam, Phys. Rev. Lett. 88, 5–8 (2002).[14] A. Kirilyuk, A. Kimel, and T. Rasing, Ultrafast optical manipulation of magnetic order,Reviews of Modern Physics 82, 2731–2784(2010).[15] K. F. Mak, K. He, J. Shan, and T. F. Heinz, Control of valley polarization in monolayerMoS(2) by optical helicity,Nature nanotechnology7, 494(2012).[16] A. E. Willner, J. Wang, and H. Huang, A different angle on light communications, Science337, 655–6(2012).[17] /cws/article/news/2012/dec/14/physics-world-reveals-its-top-10-breakthroughs-for-2012[18] M. N. Litchinitser, Structured light meets structured matter, Science 337, 1054–1055(2012).[19] K. Dholakia, and T.Čižmár, Sha ping the future of manipulation, Nature Photonics5,335–342(2011).[20] X. Sheng, Y. Zhang, F. Zhao, L. Zhang, and Y. Zhu, Effects of low-orderatmosphere-turbulence aberrations on the entangled orbital angular momentum states, Optics letters37, 2607–9(2012).[21] G. Foo, D. M. Palacios, and G. A. Swartzlander, Optical vortex corona- graph, Opt.Lett.30,3308–3310 (2005).[22] L. Marrucci, C. Manzo, and D. Paparo, Optical Spin-to-Orbital Angular MomentumConversion in Inhomogeneous Anisotropic Media, Phys Rev Lett96, 163905(2006). [23] Y. Zhao, J. Edgar, G. Jeffries, D. McGloin, and D. Chiu, Spin-to-Orbital AngularMomentum Conversion in a Strongly Focused Optical Beam, Physical Review Letters 99,073901 (2007)[24] X. L. Wang, J. Chen, Y. Li, J. Ding, C.-S. Guo,and H. T. Wang, Optical orbital angularmomentum from the curl of polarization, Physical Review Letters105(25), 1–4(2010). [25] M. Kang, Q.-H. Guo, J. Chen, B. Gu, Y. Li, and H.-T. Wang, Near-field phase singularity insubwavelength metallic microstructures, Physical Review A84(4), 1–4(2011).[26] Z. Shen, Z. J. Hu, G. H. Yuan, C. J. Min, H. Fang, and X. Yuan, Visualizing orbital angularmomentum of plasmonic vortices, 37(22), 4627–4629(2012).[27] B. J. McMorran, A. Agrawal, I. M. Anderson, A. a Herzing, H. J. Lezec, J. J. McClelland,and J. Unguris, Electron vortex beams with high quanta of orbital angular momentum, Science331(6014), 192–5(2011).[28] S. M. Mohammadi, L. K. S. Daldorff, J. E. S. Bergman, R. L. Karlsson, B. Thidé, K.Forozesh, and S. Member, Orbital Angular Momentum in Radio — A System Study, IEEE transactions on antennas and propagation58(2), 565–572(2010).[29] F. Manni, K. G. Lagoudakis, T. C. H. Liew, R. André, V. Savona, and B. Deveaud,Dissociation dynamics of singly charged vortices into half-quantum vortex pairs, Nature communications3, 1309(2012).[30] P. Cullet, L. Gil, and F. Rocca, Optical vortices, mun. 73, 403 (1989).[31] Q. Zhan, Cylindrical vector beams: from mathematical concepts to applications,Advancesin Optics and Photonics1(1), 1 (2009).[32] G. A. Siviloglou, J. Broky, A. Dogariu, and D. N. Christodoulides, Observation ofAccelerating Airy Beams, Phys. Rev. Lett.99,213901 (2007).[33] J. Durnin, J. J. J. Miceli, and J. H. Eberly, Diffraction-free beams, Phys Rev Lett58(April),1499–1501(1987).[34] I. a. Litvin, A. Dudley, A. Forbes, Poynting vector and orbital angular momentum density ofsuperpositions of Bessel beams, Optics Express19(18), 16760(2011).[35] W. Zhang, S. Liu, P. Li, X. Jiao, and J. Zhao, Controlling the polarization singularities ofthe focused azimuthally polarized beams, Optics Express21(1), 974–983 (2013).[36] J. Leach, J. Courtial, K. Skeldon, S. M. Barnett, S. Franke-Arnold, and M. J. Padgett,Interferometric methods to measure orbital and spin, or the total angular momentum of a single photon, Phys. Rev. Lett.92, 013601 (2004).[37] C. Guo, L. Lu, and H. Wang, Characterization topological charge of optical vortices byusing an annular aperture, Optics Letters34(23), 3686–3688(2009).[38] I. V. Basistiy, V. V. Slyusar, M. S. Soskin, M. V. Vasnetsov, and A. Y. Bekshaev,Manifestation of the rotational Doppler effect by use of an off-axis optical vortex beam, Optics letters28(14), 1185–1187(2003).[39] X. Gan, J. Zhao, S. Liu, and L. Fang, Generation and motion control of optical multi-vortex,Chinese Optics Letters7(12), 1142–1145(2009).[40] J. W. Haus, Z.Mozumder, and Q. Zhan, Azimuthal modulation instability for acylindricallypolarized wave in a nonlinear KerrMedium, Opt. Lett.14, 29 (2006).[41] S. M. Li, Y. Li, , X. L. Wang, L. J. Kong, K. Lou, C. Tu, and Y. Tian, Taming the collapse ofoptical fields, Scientific reports2, 1007(2012).[42] D. N. Neshev, T. J. Alexander, E. A. Ostrovskaya, Y. S. Kivshar, H. Martin, I. Makasyuk,and Z. G. Chen, Observation of discrete vortex solitons in optically induced photonic lattices, Phys. Rev. Lett.92, 123903(2004).[43] M. S. Petrović, D. M. Jović, M. R. Belić, and S. Prvanović, Angular momentum transfer inoptically induced photonic lattices, Phys. Rev. E76, 023820( 2007).[44] P. Zhang, Y. Hu, T. Li, D. Cannan, X. Yin, R. Morandotti, Z. Chen, and X. Zhang,Nonparaxial Mathieu andWeber accelerating beams, Phys. Rev.Lett.109, 193901 (2012). 2、项目的研究内容、研究目标，以及拟解决的关键科学问题（1）研究内容本项目通过理论与实验相结合的手段，探讨新型奇异光场中光子角动量的产生、测量、演化和调控，主要研究内容包括：①奇异光场中光子角动量的产生和测量通过理论分析和数值模拟揭示几种奇异光场中特殊的偏振和相位特性对产生光子角动量的规律并提出实验上实现这些角动量的方法，包括：柱对称矢量光束、艾里光束、非傍轴自弯曲无衍射光束等；进一步在实验上针对不同奇异光场产生自旋和轨道角动量；同时提出有效测量光子自旋和轨道角动量的方法并在实验上建立一套系统进行验证。
