天线方位角俯仰角以及指向计算
- 格式:docx
- 大小:212.81 KB
- 文档页数:12



一、天线的几个重要参数介绍1.天线的输入阻抗天线的输入阻抗是天线馈电端输入电压与输入电流的比值。
天线与馈线的连接,最佳情形是天线输入阻抗是纯电阻且等于馈线的特性阻抗,这时馈线终端没有功率反射,馈线上没有驻波,天线的输入阻抗随频率的变化比较平缓。
天线的匹配工作就是消除天线输入阻抗中的电抗分量,使电阻分量尽可能地接近馈线的特性阻抗。
匹配的优劣一般用四个参数来衡量,即反射系数,行波系数,驻波比和回波损耗,四个参数之间有固定的数值关系,使用那一个纯出于习惯。
在我们日常维护中,用的较多的是驻波比和回波损耗。
驻波比:它是行波系数的倒数,其值在1到无穷大之间。
驻波比为1,表示完全匹配;驻波比为无穷大表示全反射,完全失配。
在移动通信系统中,一般要求驻波比小于1.5。
回波损耗:它是反射系数绝对值的倒数,以分贝值表示。
回波损耗的值在0dB的到无穷大之间,回波损耗越大表示匹配越差,回波损耗越大表示匹配越好。
0表示全反射,无穷大表示完全匹配。
在移动通信系统中,一般要求回波损耗大于14dB。
2.天线的极化方式所谓天线的极化,就是指天线辐射时形成的电场强度方向。
当电场强度方向垂直于地面时,此电波就称为垂直极化波;当电场强度方向平行于地面时,此电波就称为水平极化波。
由于电波的特性,决定了水平极化传播的信号在贴近地面时会在大地表面产生极化电流,极化电流因受大地阻抗影响产生热能而使电场信号迅速衰减,而垂直极化方式则不易产生极化电流,从而避免了能量的大幅衰减,保证了信号的有效传播。
因此,在移动通信系统中,一般均采用垂直极化的传播方式。
另外,随着新技术的发展,最近又出现了一种双极化天线。
就其设计思路而言,一般分为垂直与水平极化和±45°极化两种方式,性能上一般后者优于前者,因此目前大部分采用的是±45°极化方式。
双极化天线组合了+45°和-45°两副极化方向相互正交的天线,并同时工作在收发双工模式下,大大节省了每个小区的天线数量;同时由于±45°为正交极化,有效保证了分集接收的良好效果。


创新实验课作业报告姓名:王紫潇苗成国学号:1121830101 1121830106 专业:飞行器环境与生命保障工程课题一双轴驱动机构转角到天线波束空间指向课题意义:随着科学技术的迅猛发展,特别是航天科技成果不断向军事、商业领域的转化,航天科技得到了极大的发展,航天器机构朝着高精度、高可靠性的方向发展。
因此对航天机构的可靠性、精度、寿命等要求越来越高,对航天器机构精度的要求显得愈发突出,无论是航天器自身的工作,还是航天器在轨服务都对其精度有着严格的要求。
航天器中的外伸指向机构通常指的是星载天线机构,星载天线是航天器对地通信的主要设备,肩负着对地通信的主要任务,同时随着卫星导航的广泛应用,星载天线就愈发的重要起来,而其指向精度的要求就愈发的突出,指向精度不足,将会导致通信信号质量下降,卫星导航精度下降等结果。
民用方面移动通信和车载导航等,军用方面舰船导航、精确打击等这些都对星载天线的指向精度有着极高的依赖性。
因此,星载天线的指向精度是非常重要的。
要保证星载天线的指向精度,首先就是要确保星载天线驱动机构在地指向精度分析的正确性,只有这样才能对接下来的在轨指向精度分析和指向误差补偿进行分析。
星载天线驱动机构的末端位姿误差主要来源于机构的结构参数误差和热变形误差,这些误差是驱动机构指向误差最原始的根源,由于受实际生产加工装配能力和空间环境的限制,这些引起末端指向误差的零部件结构参数误差是必须进行合理控制的,引起结构参数变化的热影响因素是必须加以考虑的,只有这样才能使在轨天线驱动机构指向精度动态分析和误差补偿都得到较理想的结果。
纵观整个星载天线驱动机构末端位姿误差的分析,提出源于结构参数误差和热变形误差引起的星载天线驱动机构末端位姿误差的研究是必要的。
发展现状:星载天线最初大多是以固定形式与卫星本体相连的,仅仅通过增大天线波束宽度和覆盖面积来提高其工作范围,对其精度要求不是很高,但是随着航天科技的不断发展和市场需求的不断变化,这就要求,星载天线要具备一定的自由度,因此促使了星载天线双轴驱动机构的发展。


有关罗盘也叫指北针或指南针!目前基站上用的较多的有以下几种型号和厂家的:一种哈尔滨出厂的地质罗盘、一种浙江出的地质罗盘、还有一种就是地摊上用的所谓“军用罗盘”。
一般来讲,地质罗盘的准确度较绿色的“军用罗盘”准确度要很高。
以下是针对地质罗盘的使用及测试方法:
测试方位角的方法无怪呼看黑针、看白针,这主要取决于你手持罗盘的方式及所处位置是在天线前方还是后方。
当你置身于塔下(必须身处被测小区天线正下方),面对天线时。
此时有镜子的一面冲着铁塔,你也面对铁塔。
此时如果能在镜子中看到天线,天线的地面水平线应该和镜子的中线承垂直交叉。
此时你应读取的是白针所指的方位刻度。
相反如果你手持罗盘的时有镜子的一侧对着你,此时被测小区天线仍然要被套入镜子中,其底面水平线与镜子中线承垂直交叉,此时你要读取的是黑针刻度。
通俗点说就是镜子一侧对着你自己怀里的时候,有刻度一侧指向天线覆盖正前方,但是必须要将天线套入反射镜,使其底面水平线与反射镜垂直线承垂直交叉。
此时看的是白针,反之则看黑针。
测试天线俯仰角的时候,带反射镜的一侧必须朝上,带刻度一侧必须指向地面。
此时持罗盘手的手指缓慢拨动罗盘后边的调整水平的铁片,要注意观看的是罗盘内的水平尺,此时尽量将水平尺气泡置中线,读
取水平尺所指刻度即为天线的俯仰角。
(注意事项:测试俯仰角时必须先测试抱杆的垂直度,以便保证测试精确度,带刻度一侧必须指向地面方向,反之俯仰角误差在2~3度。
)
方位角测试时罗盘应保持水平状态,避免离铁塔过近或距离手机过近。
手机磁场会象磁铁一样,导致指针失效。

卫星天线原理
卫星天线是一种用于接收和传输卫星信号的设备,通常用于卫星通信和卫星电视接收。
它们的工作原理基于以下几个方面。
1. 焦点原理:卫星天线通过将信号聚焦在一个特定的点上来增强信号强度。
天线的主要元件是一个反射器,通常是一个抛物形或拋物面。
当卫星信号在天线上照射时,它会被反射到聚焦点上,然后被天线接收器收集。
2. 方位角和俯仰角:卫星天线需要根据特定卫星的位置来调整方位角和俯仰角。
方位角是指卫星相对于观察者的水平角度,而俯仰角是指卫星相对于观察者的垂直角度。
通过调整这两个参数,卫星天线可以准确地指向特定卫星。
3. LNB(低噪声放大器):卫星天线的接收器通常包含一个LNB,它起到放大和频率转换的作用。
LNB会将接收到的信号放大,并将其转换到一个适当的频率范围内,以便传输到接收设备进行处理。
4. 天线指向控制:为了实现准确的信号接收,卫星天线通常配备一套天线指向控制系统。
这个系统可以根据卫星轨道参数和接收设备的要求,自动调整天线的方位角和俯仰角。
通常,它通过电机和传感器来实现。
5. 天气条件考虑:卫星信号的接收受天气条件的影响较大,包括降雨、云层和大气湿度等。
卫星天线通常要考虑这些因素,并在设计中采取相应的措施,以减少信号损耗并保持稳定的信
号传输。
总之,卫星天线利用反射器、聚焦原理和天线指向控制来接收和传输卫星信号,同时考虑天气条件和信号处理等因素,以确保高质量的信号接收和传输。

创新实验课作业报告姓名: 王紫潇苗成国学号:1121830101 1121830106专业:飞行器环境与生命保障工程课题一双轴驱动机构转角到天线波束空间指向课题意义:随着科学技术的迅猛发展,特别是航天科技成果不断向军事、商业领域的转化,航天科技得到了极大的发展,航天器机构朝着高精度、高可靠性的方向发展。
因此对航天机构的可靠性、精度、寿命等要求越来越高,对航天器机构精度的要求显得愈发突出,无论是航天器自身的工作,还是航天器在轨服务都对其精度有着严格的要求。
航天器中的外伸指向机构通常指的是星载天线机构,星载天线是航天器对地通信的主要设备,肩负着对地通信的主要任务,同时随着卫星导航的广泛应用,星载天线就愈发的重要起来,而其指向精度的要求就愈发的突出,指向精度不足,将会导致通信信号质量下降,卫星导航精度下降等结果。
民用方面移动通信和车载导航等,军用方面舰船导航、精确打击等这些都对星载天线的指向精度有着极高的依赖性。
因此,星载天线的指向精度是非常重要的。
要保证星载天线的指向精度,首先就是要确保星载天线驱动机构在地指向精度分析的正确性,只有这样才能对接下来的在轨指向精度分析和指向误差补偿进行分析.星载天线驱动机构的末端位姿误差主要来源于机构的结构参数误差和热变形误差,这些误差是驱动机构指向误差最原始的根源,由于受实际生产加工装配能力和空间环境的限制,这些引起末端指向误差的零部件结构参数误差是必须进行合理控制的,引起结构参数变化的热影响因素是必须加以考虑的,只有这样才能使在轨天线驱动机构指向精度动态分析和误差补偿都得到较理想的结果。
纵观整个星载天线驱动机构末端位姿误差的分析,提出源于结构参数误差和热变形误差引起的星载天线驱动机构末端位姿误差的研究是必要的。
发展现状:星载天线最初大多是以固定形式与卫星本体相连的,仅仅通过增大天线波束宽度和覆盖面积来提高其工作范围,对其精度要求不是很高,但是随着航天科技的不断发展和市场需求的不断变化,这就要求,星载天线要具备一定的自由度,因此促使了星载天线双轴驱动机构的发展。
天线的覆盖范围要紧取决于天线高度、下倾、天线增益、天线口功率、无线链路等因素。
①天线挂高:是指不算地面只算天线悬空的长度或高度。
计算方式:算建筑物的高度加支撑架到天线的中点的距离。
②方位角:正北方向的平面顺时针旋转到和天线所在平面重合所经历的角度。
在实际的天线放置中,方位角通常有0度,120度和240度。
别离对应于A小区、B小区、C小区③下倾角是天线和竖直面的夹角。
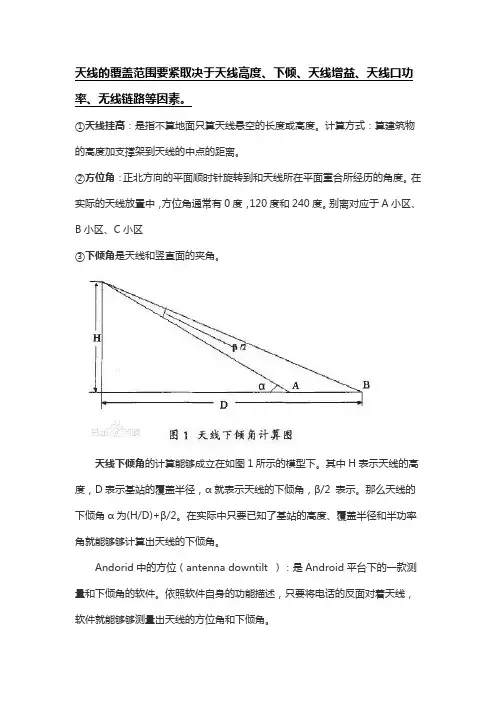
天线下倾角的计算能够成立在如图1所示的模型下。
其中H表示天线的高度,D表示基站的覆盖半径,α就表示天线的下倾角,β/2 表示。
那么天线的下倾角α为(H/D)+β/2。
在实际中只要已知了基站的高度、覆盖半径和半功率角就能够够计算出天线的下倾角。
Andorid中的方位(antenna downtilt ):是Android平台下的一款测量和下倾角的软件。
依照软件自身的功能描述,只要将电话的反面对着天线,软件就能够够测量出天线的方位角和下倾角。
天线下倾角的调整是网络优化中的一个超级重要的情形。
选择适合的下倾角能够使天线至本小区边界的射线与天线至受干扰小区边界的射线之间处于天线垂直方向图中增益衰减转变最大的部份,从而使受干扰小区的同频及邻频干扰减至最小;另外,选择适合的覆盖范围,使基站实际覆盖范围与预期的设计范围相同,同时增强本覆盖区的信号强度。
天线方向角的调整对移动通信的网络质量超级重要。
一方面,准确的方向角能保证基站的实际覆盖与所预期的相同,保证整个网络的运行质量;另一方面,依据话务量或网络存在的具体情形对方向角进行适当的调整,能够更好地优化现有的移动通信网络。
依照理想的蜂窝移动通信模型,一个小区的交壤处,如此信号相对互补。
与此相对应,在现行的GSM系统(要紧指ERICSSON设备)中,定向站一样被分为三个小区,即:A小区:方向角度0度,天线指向正北;B小区:方向角度120度,天线指向东南;C小区:方向角度240度,天线指向西南。
在GSM建设及计划中,咱们一样严格依照上述的规定对天线的方位角进行安装及调整,这也是天线安装的重要标准之一,若是方位角设置与之存在误差,那么易致使基站的实际覆盖与所设计的不相符,致使基站的覆盖范围不合理,从而致使一些意想不到的同频及邻频干扰。
天线方位角-俯仰角以及指向计算创新实验课作业报告姓名:王紫潇苗成国学号:1121830101 1121830106专业:飞行器环境与生命保障工程课题一双轴驱动机构转角到天线波束空间指向课题意义:随着科学技术的迅猛发展,特别是航天科技成果不断向军事、商业领域的转化,航天科技得到了极大的发展,航天器机构朝着高精度、高可靠性的方向发展。
因此对航天机构的可靠性、精度、寿命等要求越来越高,对航天器机构精度的要求显得愈发突出,无论是航天器自身的工作,还是航天器在轨服务都对其精度有着严格的要求。
航天器中的外伸指向机构通常指的是星载天线机构,星载天线是航天器对地通信的主要设备,肩负着对地通信的主要任务,同时随着卫星导航的广泛应用,星载天线就愈发的重要起来,而其指向精度的要求就愈发的突出,指向精度不足,将会导致通信信号质量下降,卫星导航精度下降等结果。
民用方面移动通信和车载导航等,军用方面舰船导航、精确打击等这些都对星载天线的指向精度有着极高的依赖性。
因此,星载天线的指向精度是非常重要的。
要保证星载天线的指向精度,首先就是要确保星载天线驱动机构在地指向精度分析的正确性,只有这样才能对接下来的在轨指向精度分析和指向误差补偿进行分析。
星载天线驱动机构的末端位姿误差主要来源于机构的结构参数误差和热变形误差,这些误差是驱动机构指向误差最原始的根源,由于受实际生产加工装配能力和空间环境的限制,这些引起末端指向误差的零部件结构参数误差是必须进行合理控制的,引起结构参数变化的热影响因素是必须加以考虑的,只有这样才能使在轨天线驱动机构指向精度动态分析和误差补偿都得到较理想的结果。
纵观整个星载天线驱动机构末端位姿误差的分析,提出源于结构参数误差和热变形误差引起的星载天线驱动机构末端位姿误差的研究是必要的。
发展现状:星载天线最初大多是以固定形式与卫星本体相连的,仅仅通过增大天线波束宽度和覆盖面积来提高其工作范围,对其精度要求不是很高,但是随着航天科技的不断发展和市场需求的不断变化,这就要求,星载天线要具备一定的自由度,因此促使了星载天线双轴驱动机构的发展。
地球站天线对星方法简介一、做好必要的准备:1. 准备工具:频谱仪、罗盘仪、测试电缆、扳手。
2. 参数计算:先从资料中查出天线所在地的经度Lg 、纬度φg 、所用卫星的经度Ls 。
可计算出:天线方位角()⎥⎦⎤⎢⎣⎡-+︒=g Sin Ls Lg tg Arctg Az φ180 (度)注:以正北为方位角0°天线俯仰角(度)天线极化角()⎥⎦⎤⎢⎣⎡-=g tg Ls Lg Arctg P φsin (度) 注:以地球站低噪放LNA 宽面与大地垂直时为0°基准,在天线背面,面对卫星旋转馈源。
若P 为正值,则将馈源顺时针旋转P 度,若P 为负值,则将馈源逆时针旋转P 度。
二、对星:1. 根据计算出的Az 、El 值和极化脚P 粗调天线:• 粗调俯仰:以天线中心体的背面平面作为基准,把罗盘仪的一个侧面紧靠此基准面,可以从罗盘仪上读出此天线仰角,调整俯仰调节螺杆,使天线的仰角为所需值。
• 粗调方位:一人站于天线正前方(即面对天线口面)约4~5米处,手()()⎥⎦⎤⎢⎣⎡---=Az Ls Ld g Ls Lg Arctg El sin sin cos cos 15126.0φ持水平放置的罗盘仪,旋转使之指针指向计算出的方位角。
然后另一人调整方位调节螺杆(在此时要去掉天线的方位微调螺杆),使天线中心轴指向和罗盘仪指针处于同一方向上。
•粗调馈源极化。
(此时应注意使用卫星上的信标极化)2. 细调:经过以上的调整以后,天线基本上已经对准卫星,这时再用接收机或频谱仪作为指示器,细调天线俯仰和方位。
•把频谱仪与室外单元(ODU)用测试电缆连接起来。
打开频谱仪,把频谱仪中心频率设到卫星的信标频率(若经ODU,应设到经下变频后的频率),选择适当的分辨带宽(RBW),视频带宽(VBW),扫描带宽(SPAN)等参数,使之能清楚地读出信标的指示(有一定的信噪比)。
一般设为RBW=10KHz,VBW=300KHz,SPAN=300KHz。
方位角和俯仰角的定义
方位角和俯仰角是天文学中常用的两个概念,用来描述天体在观测者视线方向上的位置。
方位角描述了天体与观测者的连线与北方向的夹角,而俯仰角则描述了天体相对于观测者视线的高度角。
方位角通常以度数来表示,从0度开始逆时针旋转,一直到360度。
当方位角为0度时,表示天体位于正北方向;90度表示东方;180度表示正南方;270度表示西方。
方位角的计算可以借助罗盘或者通过天体在天球上的坐标计算得到。
而俯仰角则表示了观测者视线与天体间的垂直夹角。
当俯仰角为0度时,表示天体位于观测者正上方;90度则表示天体在地平线上;当俯仰角超过90度时,表示天体在地平线以下。
掌握方位角和俯仰角的概念对于天文观测是至关重要的。
在进行天体观测时,观测者需要准确地确定天体在视线方向上的位置,才能精确测量其位置和运动。
方位角和俯仰角的测量也是天文仪器设计和编程的基础,帮助观测者确定观测目标的位置和朝向。
在实际观测中,观测者通常会使用专业的天文仪器来测量方位角和俯仰角。
例如,望远镜、天文定位仪等设备可以测量出星体在天球上的坐标,然后根据观测者所处地理位置,计算出相应的方位角和俯仰角。
除了天文观测,方位角和俯仰角的概念也在其他领域有所应用。
例如,无人机、导航系统、航空航天等领域都需要确定目标的方位角和俯仰角,以便准确控制和引导。
总结来说,方位角和俯仰角是天文学中用于描述天体位置的重要概念。
准确测量方位角和俯仰角对于天文观测和其他领域的定位和导航都是至关重要的。
学习和掌握方位角和俯仰角的概念将有助于我们更好地理解天文现象,并在实践中应用这些知识。
温馨小提示:本文主要介绍的是关于《精确调整天线方位角的实操指南》的文章,文章是由本店铺通过查阅资料,经过精心整理撰写而成。
文章的内容不一定符合大家的期望需求,还请各位根据自己的需求进行下载。
本文档下载后可以根据自己的实际情况进行任意改写,从而已达到各位的需求。
愿本篇《精确调整天线方位角的实操指南》能真实确切的帮助各位。
本店铺将会继续努力、改进、创新,给大家提供更加优质符合大家需求的文档。
感谢支持!(Thank you for downloading and checking it out!)《精确调整天线方位角的实操指南》一、前言在现代通信技术中,天线方位角的准确调整对于信号的稳定性和质量有着至关重要的作用。
无论是对于无线电通信、卫星通信,还是移动通信,天线的指向直接影响到传输的效率和可靠性。
因此,理解并掌握天线方位角的调整技巧,对于无线通信工程师和维护技术人员来说,都是必备的专业知识。
天线方位角调整的重要性天线方位角的调整,是指根据通信需要,精确改变天线波束的指向。
这一过程对于提高通信质量、增大覆盖范围、减少干扰和提高频率利用率等方面都有着显著影响。
例如,在无线电广播中,正确的天线方位角调整能够使得信号覆盖更加均匀,提升广播质量;在卫星通信中,方位角的微调可以确保信号的最优路径传输,降低信号衰减和延迟;在移动通信基站的建设中,通过精确的天线指向调整,可以避免或减少基站间的干扰,提高网络的整体性能。
实操指南的目的与意义本实操指南的制定,旨在为通信工程技术人员提供一套系统、实用的天线方位角调整操作指导。
通过本指南的学习,用户不仅能够了解到天线方位角调整的理论基础,更能够通过实操步骤的学习,掌握天线调整的精确方法。
此外,本指南还提供了多种情景下的实操案例,帮助读者在实际工作中遇到问题时,能够迅速找到解决方案。
本指南的内容遵循了通信技术实操的规范要求,避免理论上的抽象和脱离实际,力求使每一个实操步骤都具有可操作性和实用性。
创新实验课作业报告姓名:王紫潇苗成国学号:01 06专业:飞行器环境与生命保障工程课题一双轴驱动机构转角到天线波束空间指向课题意义:随着科学技术的迅猛发展,特别是航天科技成果不断向军事、商业领域的转化,航天科技得到了极大的发展,航天器机构朝着高精度、高可靠性的方向发展。
因此对航天机构的可靠性、精度、寿命等要求越来越高,对航天器机构精度的要求显得愈发突出,无论是航天器自身的工作,还是航天器在轨服务都对其精度有着严格的要求。
航天器中的外伸指向机构通常指的是星载天线机构,星载天线是航天器对地通信的主要设备,肩负着对地通信的主要任务,同时随着卫星导航的广泛应用,星载天线就愈发的重要起来,而其指向精度的要求就愈发的突出,指向精度不足,将会导致通信信号质量下降,卫星导航精度下降等结果。
民用方面移动通信和车载导航等,军用方面舰船导航、精确打击等这些都对星载天线的指向精度有着极高的依赖性。
因此,星载天线的指向精度是非常重要的。
要保证星载天线的指向精度,首先就是要确保星载天线驱动机构在地指向精度分析的正确性,只有这样才能对接下来的在轨指向精度分析和指向误差补偿进行分析。
星载天线驱动机构的末端位姿误差主要来源于机构的结构参数误差和热变形误差,这些误差是驱动机构指向误差最原始的根源,由于受实际生产加工装配能力和空间环境的限制,这些引起末端指向误差的零部件结构参数误差是必须进行合理控制的,引起结构参数变化的热影响因素是必须加以考虑的,只有这样才能使在轨天线驱动机构指向精度动态分析和误差补偿都得到较理想的结果。
纵观整个星载天线驱动机构末端位姿误差的分析,提出源于结构参数误差和热变形误差引起的星载天线驱动机构末端位姿误差的研究是必要的。
发展现状:星载天线最初大多是以固定形式与卫星本体相连的,仅仅通过增大天线波束宽度和覆盖面积来提高其工作范围,对其精度要求不是很高,但是随着航天科技的不断发展和市场需求的不断变化,这就要求,星载天线要具备一定的自由度,因此促使了星载天线双轴驱动机构的发展。
创新实验课作业报告姓名:王紫潇苗成国学号:1121830101 1121830106专业:飞行器环境与生命保障工程课题意义:随着科学技术的迅猛发展,特别是航天科技成果不断向军事、商业领域的转化,航天科技得到了极大的发展,航天器机构朝着高精度、高可靠性的方向发展。
因此对航天机构的可靠性、精度、寿命等要求越来越高,对航天器机构精度的要求显得愈发突出,无论是航天器自身的工作,还是航天器在轨服务都对其精度有着严格的要求。
航天器中的外伸指向机构通常指的是星载天线机构,星载天线是航天器对地通信的主要设备,肩负着对地通信的主要任务,同时随着卫星导航的广泛应用,星载天线就愈发的重要起来,而其指向精度的要求就愈发的突出,指向精度不足,将会导致通信信号质量下降,卫星导航精度下降等结果。
民用方面移动通信和车载导航等,军用方面舰船导航、精确打击等这些都对星载天线的指向精度有着极高的依赖性。
因此,星载天线的指向精度是非常重要的。
要保证星载天线的指向精度,课题一双轴驱动机构转角到天线波束空间指向首先就是要确保星载天线驱动机构在地指向精度分析的正确性,只有这样才能对接下来的在轨指向精度分析和指向误差补偿进行分析。
星载天线驱动机构的末端位姿误差主要来源于机构的结构参数误差和热变形误差,这些误差是驱动机构指向误差最原始的根源,由于受实际生产加工装配能力和空间环境的限制,这些引起末端指向误差的零部件结构参数误差是必须进行合理控制的,引起结构参数变化的热影响因素是必须加以考虑的,只有这样才能使在轨天线驱动机构指向精度动态分析和误差补偿都得到较理想的结果。
纵观整个星载天线驱动机构末端位姿误差的分析,提出源于结构参数误差和热变形误差引起的星载天线驱动机构末端位姿误差的研究是必要的。
发展现状:星载天线最初大多是以固定形式与卫星本体相连的,仅仅通过增大天线波束宽度和覆盖面积来提高其工作范围,对其精度要求不是很高,但是随着航天科技的不断发展和市场需求的不断变化,这就要求,星载天线要具备一定的自由度,因此促使了星载天线双轴驱动机构的发展。
星载天线双轴驱动机构能够实现对卫星天线的二自由度驱动,是空间环境下驱动天线运动的专用外伸执行机构。
卫星天线的二自由度运动能够满足对地通信、星间通信、卫星导航定位、以及对目标的实时观测跟踪,在满足这些需求的同时也要保证其精度的提高,随着需求的不断提高,精度已经成为衡量星载天线双轴驱动机构性能的一个重要指标,同时也是系统设计与实现的一个难点。
综上所述可以看出,星载天线双轴驱动机构是驱动卫星天线系统进行准确空间定位的核心部分。
与此同时,我国对星载天线驱动机构的研究、生产制造技术进行了一定时间的学习积累,也成功的应用到了一些卫星上,具有一定的自主能力。
自2000年后,我国在发射的卫星中,有很多采用了自主研发的天线驱动机构。
相应的研究单位也蓬勃发展,航天科技集团、上海航天局等相关单位对星载天线驱动机构的研究已经取得了很大的成就和进展。
特别是伴随着我国自主导航系统一北斗导航系统的不断发展,以及空间实验室和“嫦娥计划”的不断深入。
星载天线双轴驱动机构得到了极大地发展。
即便如此,我们跟国外还是有一定差距的,目前国内与国外的差距主要在双轴驱动机构精度、使用寿命、可靠性方面,因此还是需要进行深入研究,提高其精度、使用寿命、可靠性。
那么,我们小组也秉承着对航天事业的极大热忱开始对天线指向问题进行研究,首先我们对天线的方位角和俯仰角进行了理论的推导。
关键词:方位角俯仰角双轴定位天线指向一.天线方位角与俯仰角的计算公式推导:假定已知某时刻卫星在惯性空间的位置、速度以及天线指向点的位置信息设卫星位置矢量为P "EiRR),卫星速度矢量为V=皿必必),指向点的地理经纬度分别为B、L。
根据已知的卫星位置与速度矢量计算天线坐标系各坐标轴在惯性空间的方向矢量,计算公式:(1)X a =(V xi,V yi,V zi)T =(X Xay,X az)T12 2 2 \ P xi , P yi ,P zi(-P zi,-P yi ,-P Xi)T=(Z ax, Z ay , Z az )Y a = Z a =X a根据指向点的相关参数计算指向点在惯性空间的位置坐标(S: , S,, S:), 首先计算指向点在地固坐标系中的坐标,计算公式为:(2)S x c = (N H )cos B cos LS yc = (N H )cos BcosLS zc珂N(1 —e)2 H]sin Ba e2 2 2B (1—e) sin B1e =98.257(3)将地固坐标系中的坐标转换到惯性坐标系中cosGST-sin GST o]Se、‘S ze cosGST —S ye sin GST 'S y=sin GST cosGST0Sye=S ze si nGST + S e cosGST l S x丿< 00b l S ze 丿l S zeJ (4) 式中GST是当时的格林尼治恒星时角;由图3得:T sa 二S-R于是有:(5)T Sa z = Sz - P ziTSa y 二S y - P yiR是地球赤道平均半径OS 图3 卫星地球指向点位置示意图二S x - 巳7(6)计算俯仰角cos -T saL Z a T sa 区TSa x忆 axTSa y _Z ayTSa^ —ZaxR xa2 - Z ay 2 Z az 2(7)计算天线方位角:'TSa< Mx +T Sa y Nay +T S®sin :r ya R ita sin :■'TSa x Mx *T Sa y L X ay_k azcos :二 ---------- ----------- 式中 %R Sasin :R S^ .T Sa Ty S ^Tz Sa S 是向量Y a 的长度,r xa 是向量X a 的长度。
(8)按照星本体3— 1— 2顺序定义姿态角,设'、二、分别是偏航、俯仰和滚 动角。
在考虑轨道运动的基础上,进一步考虑卫星姿态变化时最终的天线方向角 计算公式如下:考虑偏航角时的天线方向角:,',(9)偏航和滚动角变化时天线方向角:,-',■■ ■■:=arccos(-sin sin : .sin :心 亠 cos cos 1-1』 cos©sin B 即sin a\g+sin cos: 二 arctan()sin I-L eos -:©(10)偏航、滚动和俯仰角变化时天线方向角::---■ ■■d - arccos(sin^sin I wcos :g.‘亠 cos^ cos "]) sin P 軸sin ^轴 :「匕-arcM)cos^sin P 轴cosa 舛—sin# cosP 聊如图4所示,已知指向点L 、B 、H ,根据某一时刻卫星位置矢量和速度矢量,以 及卫星的姿态角'、,、:下面顺序计算就可得到天线的方向角1)用公式⑴〜⑺计算考虑卫星轨道变化时的天线方向角:> ;國4天翳向駢純册二.双轴定位点波束指向问题1.天线波束指向计算已知双轴定位机构转角求反射线的空间指向比较容易,而根据反射线的空间指向计算机构转角则可以归结为一个非线性方程求解问题,无法得到方程的解析解,只能通过数值方法得到数值近似解。
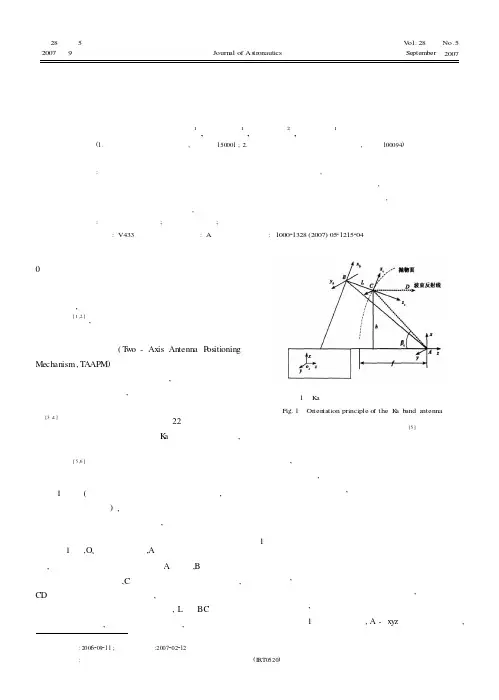
取如图1所示坐标系,A-XYZ为焦点坐标系‘B-X b XZ b为定位机构转动坐标系,°一X c Y c Z c为抛物面反射中心固联坐标系,图中h为初始时天线反射中心在焦点坐标系A-XYZ下到yz平面的高度,Bc为入射线AC与yz平面的夹角, f为反射抛物面的焦距。
则在A-XYZ坐标系下,反射抛物面方程2 2为:X y =4f(z f),B的坐标为:厂/MW1.1从定位机构转角计算波束指向若双轴定位机构转角大小为绕Yb 轴的转A 角,绕Xb 轴的旋转角B,空间任意点在 坐标系° —XMZ c 与A —XYZ 的变换可以通过方向余旋矩阵及平移向量来描述: 5小也一兀心T 0 T ,其中,在这个式子中各个物理量的定义如下:U -空间任意点在A-XYZ 的坐标; U4 -空间任意点在。
-乂况乙。
的坐标; T1 -从点A 到点B 的平移向量; T4 -从点B 到点C 的平移向量;Di -旋转变换矩阵(i = 1,2, 3)T 1 -^Lsin(》—h,0, L T 4 = >0 0 -L T到原焦点在C-X c Y c Z 坐标系下的坐标 U4 ,相应的反射线CD的单位矢量在D2= D 2XD 3 二 D 3ycos(-%) 0 sin (-%) 1 0 -sin (-彩)10 cos ^B 2)0 —si ncos : 00 1 sin P cos : -sin :- I 0 cos :L T为馈源焦点在天线焦点坐标系下的坐标,则代入上式(3),得K a 点波束天线双轴定位原理示意图(f -h 24f)]T该单位矢量在A-XYZ 坐标下的分量可表示为应用上述方法只能完成从机构转角到天线波束指向的计算 ,而从天线波束指向计算所需的机构转角则存在一定困难 ,一般均通过预先编制计算机构转角与波 束指向角的对应关系表的方案来解决此问题。
1.2波束指向计算定位机构转角据几何光学原理可知,如图2所示的直线BC 、CD 、BA 、CA 共面,设反射线CD 的反向延长线与BA 交于E 点。
设平面图形中的夹角如图2所示,则向量BA 已知,向量CD 的单位向量已知,有由平面三角几何有:s i n( - J _)si n_(s i)n片)lb alb a lb c上式是单变量H 的非线性超越函数,可变形为:f(8)=bc SiB(-)ba上述非线性方程可由非线性方程的数值解法求得,这样将从指向角到定位机构转角的双变量变换转化为以 H 为单变量的非线性方程求根问题 ,可以证明方程(15)在[0, 45)范围内有唯一根。
从而点E( XE ,*,ZE )、点C( 的坐标可由三角形的正弦定理通过下式求:C -X c Y c Z 下的分量形式为:R cI - X4R a =〔XRay RaD 2 D i f LRcco 弐=)-y4从波束指向角反解机构转角示意图Fig. 2 Calculation of the rotate angle by beam pointingCD 从而得到在坐标系A - xyz 下描述的向量BC 为:BC A= C B而BC 在天线面坐标系&下可描述为0 0 lb^ ,因而有: D 3 D 2|_1° 0he 丨=D |iBCA因而有:BA EG 说I be S i n -I bc COSJbeCOSs i :n=D 1BC A通过上式即可求得双轴机构所需转角课题二地球同步轨道卫星理想轨道计算模型这部分我们分两部分进行,第一部分是卫星的发射阶段,第二阶段是在轨运行阶段。