下载文档原格式
九年级黄金分割知识点课程黄金分割是数学中的一个重要概念，也是美学中常见的一种比例关系。
在九年级的数学课程中，学生将接触到这一知识点，并深入了解其应用。
本文将围绕九年级黄金分割知识点课程展开讲述，包括黄金分割的定义、性质、推导方法以及一些实际应用。
一、黄金分割的定义黄金分割是指一条线段分成两部分，较大部分与整体的比值等于较小部分与较大部分的比值。
用数学符号表示为a/b=(a+b)/a=Φ （phi），其中Φ为黄金分割常数，约等于1.618。
二、黄金分割的性质1. 黄金分割点对称性：在一条线段上，黄金分割点将这条线段分成两部分，这两部分的比值等于整体线段与较大部分的比值。
2. 黄金分割点的延伸：无论是将整体线段延伸至左侧还是右侧的与原线段等比例的线段，其分割点仍然是黄金分割点。
3. 黄金矩形性质：将一个正方形的一边延伸至黄金分割点，形成的长方形即为黄金矩形。
黄金矩形具有自相似性和美学上的和谐感。
三、黄金分割的推导方法黄金分割的推导方法主要有几何法和代数法两种。
1. 几何法：通过将线段分割，得到与之相似的子线段，并运用相似三角形的性质，可以推导出黄金分割比例。
2. 代数法：假设整体线段为a，较小部分的长度为b，根据黄金分割的定义可得到a/b = (a+b)/a，解方程可得黄金分割比例。
四、黄金分割的实际应用黄金分割不仅在数学中有重要意义，也在自然界和人类创作中有广泛应用。
1. 建筑设计：许多古代和现代的建筑作品都运用了黄金分割比例，如古代希腊建筑中的帕特农神庙和现代的肯尼迪图书馆。
2. 绘画和摄影：黄金分割比例用于画面的构图和角度的选择，可以使画面更加美观和和谐。
3. 音乐和舞蹈：黄金分割比例用于音乐中的乐谱结构和舞蹈中的动作设计，可以营造出一种流畅而和谐的感觉。
4. 金融市场：黄金分割被应用于金融领域的技术分析中，用于预测价格波动和市场趋势。
总结：九年级的黄金分割知识点课程涵盖了黄金分割的定义、性质、推导方法和实际应用。
黄金分割（Golden Ratio）是指一个数与其倒数之和等于1的比例关系，即a与1/a的比值等于1、黄金分割在数学、艺术和自然科学中都有广泛应用。
下面是关于黄金分割的九年级数学知识点的详细介绍。
1.黄金分割的定义：黄金分割是指一个数与其倒数之和等于1的比例关系。
用数学符号表示为a+1/a=1、解这个方程可以得到黄金分割的值，约为1.6182.黄金分割的性质：-黄金分割具有对称性：即a+1/a=1，所以a的倒数也是它的黄金分割点。
-黄金分割点的平方等于黄金分割点加1，即a²=a+1-黄金分割点与1的比值等于黄金分割点减1与1的比值，即a/1=(a-1)/a。
-黄金分割点与1的差与黄金分割点的比值等于1与黄金分割点的比值，即a-1/a=1/a。
3.黄金分割的几何应用：-黄金矩形：在一个长宽比例为黄金分割的矩形中，可以将矩形不断分割为一个正方形和一个长宽比例仍为黄金分割的矩形。
这种分割方式可以无限进行下去。
-黄金三角形：在一个等腰三角形中，底边与等腰边的比例为黄金分割。
黄金三角形有一些独特的几何性质，如旋转、平移和缩放等操作都能保持黄金三角形的形状。
4.黄金分割的代数应用：-黄金分割的计算：利用黄金分割的定义，可以解出黄金分割的值。
这可以通过求解二次方程a²-a-1=0来实现。
-黄金比例的性质：黄金分割可以满足一些特殊的性质，如将一条线段分割为黄金分割点后，两个线段的比值等于原线段与较短线段的比值，也等于较长线段与原线段的比值。
这个比例具有稳定性，无论线段的长度如何变化，比值都保持不变。
-黄金分割的近似值：黄金分割可以用连分数或迭代法来逼近其值。
连分数是一种无限循环小数的表示方法，可以得到黄金分割的连分数表示为1+1/(1+1/(1+1/(1+...)))。
5.黄金分割的艺术应用：-黄金比例在绘画和建筑艺术中被广泛应用。
很多伟大的艺术家和建筑师使用黄金分割来构图和设计。
黄金分割可以使作品更加和谐、对称和美观。
九年级数学黄金分割知识点黄金分割是一种美学原则，也是一种数学概念。
它源自古希腊艺术与建筑，被广泛应用于文化和设计领域。
黄金分割是一种比例关系，其比值约为1:1.618。
在九年级数学中，黄金分割也是一个重要的知识点，它与数列、图形等内容密切相关。
一、黄金分割比例黄金分割比例是指一个线段一分为二时，较长部分与整体的比值等于整体与较短部分的比值。
即如果将一个线段分成两部分，较长部分与整体的比值约等于1.618，而较短部分与整体的比值约等于0.618。
这个比例是无限不循环小数，被简化为1.618。
二、黄金分割的应用黄金分割在几何学和自然科学中有广泛的应用。
在几何学中，一些特殊的图形，如黄金矩形和黄金三角形，具有黄金分割的性质。
黄金矩形是指长和宽之比为黄金分割比例的矩形。
黄金三角形是一个直角三角形，其两条腰的比例接近黄金分割。
这些图形在建筑和设计中被广泛使用，给人一种美感和和谐感。
黄金分割还与数列和斐波那契数列有密切关系。
斐波那契数列是一个无限序列，每个数字是前两个数字之和。
斐波那契数列的前两个数字是1，1，然后依次为2，3，5，8等等。
当我们计算斐波那契数列中相邻数字的比值时，会发现它们逐渐接近黄金分割比例。
例如，5/3≈1.667，8/5≈1.6，13/8≈1.625。
这种关系在数学中被广泛探讨，可以通过递归公式定义斐波那契数列。
三、黄金分割与美学黄金分割被认为是一种美学原则，用于艺术和设计中。
在绘画、摄影、雕塑等艺术形式中，黄金分割被用来划分画面，使得画面更加平衡和美观。
例如，在绘画中，艺术家可以将水平和垂直线分为黄金分割比例的两部分，以创建一种独特的视觉效果。
黄金分割也被应用于肖像摄影和建筑设计中，以达到更好的组合和比例感。
四、黄金分割的历史黄金分割作为一个数学概念，最早由古希腊数学家欧几里得提出。
在欧几里得的《几何原本》中，他给出了一种构造黄金分割比例的方法。
随后，黄金分割在文艺复兴时期再次受到重视，成为艺术和建筑中的一个重要原则。
初三数学黄金分割笔记
黄金分割是初三数学中的一个重要概念，它在几何、代数、三角函数等方面都有广泛的应用。
以下是初三数学黄金分割的笔记：- 黄金分割的定义：如果一个线段被分割成两段，使得较长线段与全长的比值等于较短线段与较长线段的比值，那么这个分割点就叫做黄金分割点，这个比值就叫做黄金分割数。
- 黄金分割数的计算公式：黄金分割数通常用希腊字母表示，它的计算公式为：
- 黄金分割在几何中的应用：在矩形中，如果长和宽的比等于黄金分割数，那么这个矩形就叫做黄金矩形。
黄金矩形具有很多美学性质，如宽与长的比是黄金分割数，对角线与长的比也是黄金分割数等。
- 黄金分割在代数中的应用：在一元二次方程中，如果二次项系数和一次项系数的比等于黄金分割数，那么这个方程的根就是黄金分割数。
- 黄金分割在三角函数中的应用：在正五边形中，如果边长与对角线的比等于黄金分割数，那么这个正五边形的内角和就等于540 度。
黄金分割在数学中有很多应用，它不仅具有美学价值，还在实际生活中有很多应用，如建筑设计、艺术创作、金融投资等。
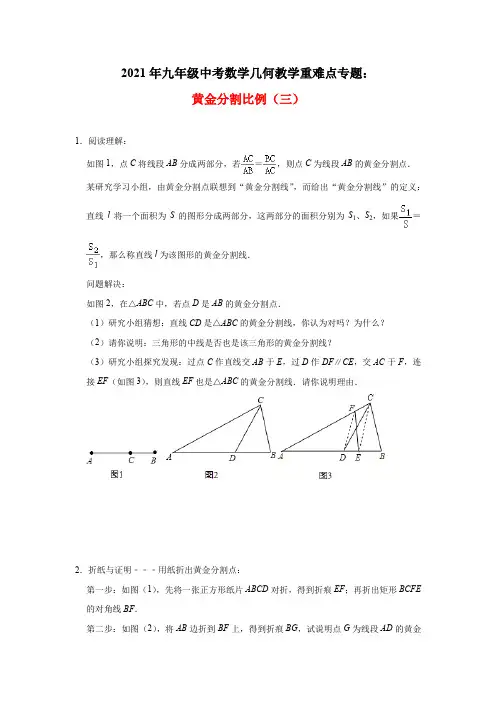
2021年九年级中考数学几何教学重难点专题：黄金分割比例（三）1．阅读理解：如图1，点C将线段AB分成两部分，若＝，则点C为线段AB的黄金分割点．某研究学习小组，由黄金分割点联想到“黄金分割线”，而给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果＝，那么称直线l为该图形的黄金分割线．问题解决：如图2，在△ABC中，若点D是AB的黄金分割点．（1）研究小组猜想：直线CD是△ABC的黄金分割线，你认为对吗？为什么？（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？（3）研究小组探究发现：过点C作直线交AB于E，过D作DF∥CE，交AC于F，连接EF（如图3），则直线EF也是△ABC的黄金分割线．请你说明理由．2．折纸与证明﹣﹣﹣用纸折出黄金分割点：第一步：如图（1），先将一张正方形纸片ABCD对折，得到折痕EF；再折出矩形BCFE 的对角线BF．第二步：如图（2），将AB边折到BF上，得到折痕BG，试说明点G为线段AD的黄金分割点（AG＞GD）3．若一个矩形的短边与长边的比值为（黄金分割数），我们把这样的矩形叫做黄金矩形．（1）操作：请你在如图所示的黄金矩形ABCD（AB＞AD）中，以短边AD为一边作正方形AEFD；（2）探究：在（1）中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由．4．三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB＝AC，且∠A＝36°．（1）在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；（2）△BCD是不是黄金三角形？如果是，请给出证明；如果不是，请说明理由；（3）设，试求k的值；（4）如图2，在△A1B1C1中，已知A1B1＝A1C1，∠A1＝108°，且A1B1＝AB，请直接写出的值．5．在数学上称长与宽之比为黄金分割比的矩形为黄金矩形，如在矩形ABCD中，当时，称矩形ABCD为黄金矩形ABCD．请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成．6．图1是一张宽与长之比为的矩形纸片，我们称这样的矩形为黄金矩形．同学们都知道按图2所示的折叠方法进行折叠，折叠后再展开，可以得到一个正方形ABEF 和一个矩形EFDC，那么EFDC这个矩形还是黄金矩形吗？若是，请根据图2证明你的结论；若不是，请说明理由．7．如图1所示，点C将线段AB分成两部分，如果，那么点C为线段AB的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1、S2，如果，那么称直线l为该图形的黄金分割线．（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点，如图2所示，则直线CD是△ABC的黄金分割线，你认为对吗？说说你的理由；（2）请你说明：三角形的中线是否是该三角形的黄金分割线．8．在△ABC中，AB＝AC，∠A＝36°，把像这样的三角形叫做黄金三角形．（1）请你设计三种不同的分法，将黄金三角形ABC分割成三个等腰三角形，使得分割成的三角形中含有两个黄金三角形（画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法，不要求证明．分别画在图1，图2，图3中）注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法．（2）如图4中，BF平分∠ABC交AC于F，取AB的中点E，连接EF并延长交BC的延长线于M．试判断CM与AB之间的数量关系？只需说明结果，不用证明．答：CM与AB之间的数量关系是．9．“黄金分割”在人类历史上有着重要的作用和影响，世界上许多著名的建筑和艺术品中都蕴涵着“黄金分割”．下面我们就用黄金分割来设计一把富有美感的纸扇：假设纸扇张开到最大时，扇形的面积与扇形所在圆的剩余部分的比值等于黄金比，请你来求一求纸扇张开的角度．（黄金比取0.6）10．如图，在△ABC中，点D在边AB上，且BD＝DC＝AC，已知∠ACE＝108°，BC＝2．（1）求∠B的度数；（2）我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比（或者底边长与腰长的比）等于黄金比．①写出图中所有的黄金三角形，选一个说明理由；②求AD的长．参考答案1．解：（1）直线CD 是△ABC 的黄金分割线．理由如下： ∵点D 是AB 的黄金分割点，∴＝，∵＝，＝，∴＝，∴直线CD 是△ABC 的黄金分割线；（2）∵三角形的中线把AB 分成相等的两条线段，即AD ＝BD ， ∴＝，＝＝1，∴三角形的中线不是该三角形的黄金分割线；（3）∵DF ∥CE ，∴S △FDE ＝S △FDC ，S △DEC ＝S △FEC ，∴S △AEF ＝S △ADC ，S 四边形BEFC ＝S △BDC ，∵＝，∴＝，∴直线EF 是△ABC 的黄金分割线．2．证明：如图，连接GF ，设正方形ABCD 的边长为1，则DF ＝． 在Rt △BCF 中，BF ＝＝，则A ′F ＝BF ﹣BA ′＝﹣1． 设AG ＝A ′G ＝x ，则GD ＝1﹣x ，在Rt △A ′GF 和Rt △DGF 中，有A 'F 2+A 'G 2＝DF 2+DG 2， 即，解得x＝，即点G是AD的黄金分割点（AG＞GD）．3．解：（1）如图：以A为圆心，在AB上截取AE＝AD，以D为圆心，在DC上截取DF＝DA，连接EF，所以四边形AEFD为所求作的正方形；（2）答：四边形EBCF是黄金矩形．证明：∵四边形AEFD是正方形，∴∠AEF＝90°，∴∠BEF＝90°，∵四边形ABCD是矩形，∴∠B＝∠C＝90°∴∠BEF＝∠B＝∠C＝90°，∴四边形EBCF是矩形．设CD＝a，AD＝b，则有，∴，∴矩形EBCF是黄金矩形．4．解：（1）如图所示；（2）△BCD是黄金三角形．证明如下：∵点D在AB的垂直平分线上，∴AD＝BD，∴∠ABD＝∠A．∵∠A＝36°，AB＝AC，∴∠ABC＝∠C＝72°，∴∠ABD＝∠DBC＝36°．又∵∠BDC＝∠A+∠ABD＝72°，∴∠BDC＝∠C，∴BD＝BC，∴△BCD是黄金三角形．（3）设BC＝x，AC＝y，由（2）知，AD＝BD＝BC＝x．∵∠DBC＝∠A，∠C＝∠C，∴△BDC∽△ABC，∴，即，整理，得x2+xy﹣y2＝0，解得．因为x、y均为正数，所以．（4）．理由：延长BC到E，使CE＝AC，连接AE．∵∠A＝36°，AB＝AC，∴∠ACB＝∠B＝72°，∴∠ACE＝180°﹣72°＝108°，∴∠ACE＝∠B1A1C1．∵A1B1＝AB，∴AC＝CE＝A1B1＝A1C1，∴△ACE≌△B1A1C1，∴AE＝B1C1．由（3）知，∴，，∴．5．证明：在AB上截取AE＝BC，DF＝BC，连接EF．∵AE＝BC，DF＝BC，∴AE＝DF＝BC＝AD，又∵∠ADF＝90°，∴四边形AEFD是正方形．BE＝，∴，∴矩形BCFE的宽与长的比是黄金分割比，矩形BCFE是黄金矩形．∴黄金矩形是由一个正方形和一个更小的黄金矩形构成．6．解：矩形EFDC是黄金矩形，证明：∵四边形ABEF是正方形，∴AB＝DC＝AF，又∵，∴，即点F是线段AD的黄金分割点．∴，∴，∴矩形CDFE是黄金矩形．7．解：∵，，又∵D是AB的黄金分割点，∴，，∴CD是△ABC的黄金分割线；（2）不是．∵CD是△ABC的中线，∴AD＝DB，∴＝，而＝1，∴≠，∴中线不是黄金分割线．8．解：（1）（3分）（2）CM＝AB（4分）9．解：设扇形的半径为R，圆心角为n，则剩余扇形的圆心角为（360°﹣n），由题意得，：＝0.6，即n：（360°﹣n）＝0.6，解得：n＝135，答：纸扇张开的角度为135°．10．解：（1）设∠B＝x，∵BD＝DC，∴∠DCB＝∠B＝x，∴∠ADC＝∠B+∠DCB＝2x，∵AC＝DC，∴∠A＝∠ADC＝2x，∵∠ACE＝∠B+∠A，∴x+2x＝108°，解得x＝36°，即∠B的度数为36°；（2）①△ABC、△DBC、△CAD都是黄金三角形．理由如下：∵DB＝DC，∠B＝36°，∴△DBC为黄金三角形；∵∠BCA＝180°﹣∠ACE＝72°，而∠A＝2×36°＝72°，∴∠A＝∠ACB，而∠B＝36°，∴△ABC为黄金三角形；∵∠ACD＝∠ACB﹣∠DCB＝72°﹣36°＝36°，而CA＝CD，∴△CAD为黄金三角形；②∵△BAC为黄金三角形，∴＝，而BC＝2，∴AC＝﹣1，∴CD＝CA＝﹣1，∴BD＝CD＝﹣1，∴AD＝AB﹣BD＝2﹣（﹣1）＝3﹣．。
6.2 黄金分割
1．知识与技能目标：
（1）了解黄金分割的概念，求作任意线段的黄金分割点；
（2）进一步理解线段的比，增强知识的综合运用能力．
2．过程与方法目标：
（1）通过现实情境与素材加强对线段的比的认识，了解黄金分割的文化价值；
（2）培养学生的实践意识、动手能力和自主学习的能力．
3．情感与态度目标：
（1）从学生乐于接受的现实背景中学习黄金分割，认识到数学是解决实际问题和进行交流的重要工具；
（2）通过对黄金分割的理解和掌握，明确黄金分割的作图方法，体会数形结合的思想；
（3）通过分组讨论学习，体会在解决实际问题的过程中与他人合作的重要性，从而培养学生的团结协作精神．了解黄金分割的意义，并能作出线段的黄金分割点．
会用线段的黄金分割来解决一些实际问题．
例说明黄金分割在生活中的应用吗？。
