当前位置：文档之家 › 哈工大版理论力学答案详解第11章

哈工大版理论力学答案详解第11章

  • 格式：pdf
  • 大小：2.16 MB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

理论力学第11章习题答案

理论力学第11章习题答案

四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
我在沙滩上写上你的名字，却被浪花带走了；我在云上写上你的名字，却被风儿带走了；于是我在理论力 学的习题答案上写上我的名字.
11.8 如图所示，重物 M 系于弹簧上，弹簧的另一端则固定在置于铅垂平面内的 圆环的最高点 A 上。重物不受摩擦地沿圆环滑下，圆环的半径为 20 cm ，重物的 质量为 5 kg ，如重物在初位置时 AM 20 cm ，且弹簧具有原长，重物的初速度 等于零，弹簧的重量略去不计，欲使重物在最低处时对圆环的压力等于零，弹簧 刚性系数应为多大？
11.5 计算图示各系统的动能 (1)如图(a)所示，质量为 m 、长为 l 的均质圆盘在自身平面内作平面运动，已知圆 盘上 A 、 B 两点的速度方向， B 点的速度为 vB ， 45 ； (2)如图(b)所示，质量为 m1 的均质杆 OA 、一端铰接在质量为 m2 的均质圆盘中心， 另一端放在水平面上，圆盘在地面上作纯滚动，圆心速度为 v ； (3)如图(c)所示质量为 m 的均质细圆环半径为 R ，其上固结一个质量也为 m 的质 点 A ，细圆环在水平面上纯滚动，图示瞬时角速度为 。
魏 魏 魏
泳
F ) 2
涛 涛 涛
解： 滚阻力偶： M N (mg 轮转动角度：
x R
将力 F 向 C 简化， F 对 C 主矩： M C Fr
F sin 60 x M C M
3 FR x F x 总功： Fx (mg ) 2 2 R 2 R Fx F x (1 3 ) (mg ) 2 2 R
涛 涛 涛
解：
1 l 2 (2m)l 2 2m ( ) 2 ml 2 12 3 3 滑块 A 的速度： vA l cos sin 滑块 B 的速度： vB l 1 2 1 2 1 2 5 2 2 系统动能： J D mvA mvB ml 2 2 2 6 l 重力功： (sin 0 sin ) 2mg l (sin 0 sin ) mg 2mgl(sin 0 sin ) 2 1 弹性力功： k[l 2 (1 cos 0 ) 2 l 2 (1 cos ) 2 ] 2 根据动能定理： 5 2 2 1 ml 0 2mgl(sin 0 sin ) k[l 2 (1 cos 0 ) 2 l 2 (1 cos ) 2 ] ( 1 ) 6 2 当 0 60 、 0 时，

理论力学(第七版)课后题答案哈工大

理论力学(第七版)课后题答案哈工大
理论力学（第七版）课后题答案 哈工大.高等教育出版社
第1章 静力学公理和物体的受力分析
1-1 画出下列各图中物体 A，ABC 或构件 AB，AC 的受力图。未画重力的各物体的自 重不计，所有接触处均为光滑接触。
FN 1
A
P FN 2
(a)
(a1)
FT A P FN
(b)
A
(b1)
FN1
P
B FN 3
FR = (80i + 140 j ) N
FR = (80 N) 2 + (140 N) 2 = 161 N
2-2 如图 2-2a 所示，固定在墙壁上的圆环受 3 条绳索的拉力作用，力 F1 沿水平方向， 力 F3 沿铅直方向，力 F2 与水平线成 40°角。3 个力的大小分别为 F1=2 000 N，F2=2 500 N， F3=1 500 N。求 3 个力的合力。
C
FN 2
′ FN
B
P2
(a1)
FN1
(a) FN 1
B
C P2 FAy A
FN 2
FN
P1
P1
FAy
A F Ax
FAx
(a2)
(a3)
FN1
A P1 B P2
FN 3
FN 2
(b)
(b1)
′ FN
FN 1
A
B P2
FN 3
P1
FN
FN 2
(b3)
(b2)
3
理论力学（第七版）课后题答案 哈工大.高等教育出版社
F2 = 173 kN
如图 2-5a 所示，刚架的点 B 作用 1 水平力 F，刚架重量不计。求支座 A，D 的约
y F B C x

哈尔滨工业大学理论力学课后习题问题详解

哈尔滨工业大学理论力学课后习题问题详解

实用标准文档----------------------------------------理论力学（第七版）课后题答案 哈工大.高等教育出版社-------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ，ABC 或构件 AB ，AC 的受力图。

未画重力的各物体的自重不计，所有接触处均为光滑接触。

F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e)(e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2(h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB ′ F AC CA′ F ABBF ACF BAA P (l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。

题图中未画重力的各物体的自重不计，所 有接触处均为光滑接触。

F N 2C′ F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)′ F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxACD F N2B P2P1F N1(c) (c1)F AyF TA F AxD′FF N2 TBP1F N1 P2(c2) (c3)F AyF BqBA FAxC DF C(d) (d1)F DyF Ay F BqqD′FDxBA F Ax C F Dx D′FDyF C(d2) (d3)F Ay′FBxq BF AyF AxqA B ′FByF AxF Cx CF Cy PF BxA BPF Cx(e1)C F By F Cy(e) (e2) (e3)F1 CF2F Ay FByA BF Ax F Bx(f) (f1)F Cx′ FCxCCF 1F CyF ′ F 2 F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)′ F CyF T′FCxCF AyF BF TDCF AxBAF Cx P (g2)(g3)DF 1F CyF B ′ F 2F BBCF CxBF Ay AF Ax(h)(h1)(h2)A F AxF AyF CyF CxC′ A F EF CyF F OyCDF OxF Cx ′EO B(i)(i1)(i2)AA ′FAx′FE′FAyFEC DF ByF ByF OyF BxF Ox F BxOB B(i3) (i4)F AyD EF CxF TA F AxF ByCCH FBy F CyB PF Bx F BxB(j) (j1) (j2)F Ay F Dy′′FEy′F CF Cx′E F AxT 2D F T 2 ′FExF Ex A D F Dx′ EF DxF T3F T1 ′FCyF Dy F Ey(j3) (j4) (j5)EF F BC ED ′ BFCxθ′′FDEFCy(k) (k1)F BFFCB FCxθ E CF Cy90°−θFDED DF AyF AyA AF Ax F Ax(k2) (k3)F B′ FBF 1F DBBDCAF AF C(l)(l1)(l2)F 2′ D F DF 1F 2D BAC EE F EF AF C F E(l3)(l4)或′ ′ F DyF 2F 1F F Dy F 2F 1B ′ DF DxF DxBBD D F ExA C E C E F ExF CF EyF AF CF Ey(l2)’(l3)’ (l4)’′ F ADAF CyF CxCF 1B(m)(m1)F ADDF ADHEF 2A DF EF HF AD ′(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq′ F BF N 2F N3(n2)FB D FF C F E F AF G GCEA(o)(o1)FBBDFDF BF E F F F CF D′ FEA F AF B ′ CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ，B 和 C 处受 3个力作用，如图 2-1a 所示。

理论力学(盛冬发)课后习题答案ch11资料

理论力学(盛冬发)课后习题答案ch11资料
第11章 动量矩定理 ·127·
127· R O 2 Q (b) (a) R O 1 Q 图11.28 三、选择题 1. 均质杆AB，质量为m，两端用张紧的绳子系住，绕轴O转动，如图11.29所示。则杆AB对O轴的动量矩为 A 。 (A) 265ml (B) 21213ml (C) 234ml (D) 2121ml 2. 均质圆环绕z轴转动，在环中的A点处放一小球，如图11.30所示。在微扰动下，小球离开A点运动。不计摩擦力，则此系统运动过程中 B 。 (A) 不变，系统对z轴的动量矩守恒 (B) 改变，系统对z轴的动量矩守恒 (C) 不变，系统对z轴的动量矩不守恒 (D) 改变，系统对z轴的动量矩不守恒 3. 跨过滑轮的轮绳，一端系一重物，另一端有一与重物重量相等的猴子，从静止开始以速度v向上爬，如图11.31所示。若不计绳子和滑轮的质量及摩擦，则重物的速度 B 。 (A) 等于v，方向向下 (B) 等于v，方向向上 (C) 不等于v (D) 重物不动 A B l O l l r A z 图11.29 图11.30 4. 在图11.32中，摆杆OA重量为G，对O轴转动惯量为J，弹簧的刚性系数为k，杆在铅垂位置时弹簧无变形。则杆微摆动微分方程为 D (设sin)。 (A) GbkaJ2 (B) GbkaJ2 (C) GbkaJ2 (D) GbkaJ2
第11章 动量矩定理 ·129·
129· 示。试求各物体对通过点O并与图面垂直的轴的动量矩。 (a) O A l O R C (c) (b) O R 图11.35 解：（a）杆OA对通过点O并与图面垂直的轴的动量矩为 231mlJLOO （b）圆盘对通过点O并与图面垂直的轴的动量矩为 221mRJLOO （c）圆盘对通过点O并与图面垂直的轴的动量矩为 22223)21(mRmRmRJLOO 11-2 如图11.36所示，鼓轮的质量11800kgm，半径025mr.，对转轴O的转动惯量2853kgmOJ.。现在鼓轮上作用力偶矩0743kNmM.来提升质量22700kgm的物体 A。试求物体A上升的加速度，绳索的拉力以及轴承O的反力。绳索的质量和轴承的摩擦都忽略不计。 解：（1）选整体为研究对象，受力分析如图所示。应用质点系动量矩定理，有 grmMrmJO2022)( 解得鼓轮转动的角加速度为 )/(21.325.027003.8525.08.927007430222220sradrmJgrmMO 物体A上升的加速度为 )/(8.02smraA （2）要求绳索的拉力，可选物体 A为研究对象，受力分析如图所示。应用质点运动微分方程，有 gmFamT22 解得绳索的拉力为 )(62.288.027008.9270022kNamgmFT （3）要求轴承O的反力，可选鼓轮为研究对象，受力分析如图所示。应用质心运动定

哈尔滨工业大学理论力学第七版W第11章 动量矩定理

哈尔滨工业大学理论力学第七版W第11章 动量矩定理

m v C
e
d LC dt
r
d rC dt
C
Fi
e
ri ' Fi
由于
vC ,
d rC dt
m vC 0
rC
d dt
m v C
e
rC F i
e

得
rC Fi
d LC dt
rC Fi
r 'i Fi
e
投影式 L M (m v ) L z z i i O

z
* 刚体的动量矩 1．平动刚体
L r m v m r v r mv
O i i i i i C C
C
L z M z ( m vC )
平动刚体对固定点（轴）的动量矩， == 刚体质心的动量(具有刚体的质量）对 该点（轴）的动量矩。
2 2
FOy 2 mg ma C 1 y ma C 2 y
2 8 9 . 8 8 ( 20 . 75 0 . 25 20 . 75 0 . 5 )
32 . 3 N
§11-5 质点系相对于质心的动量矩定理
1．对质心的动量矩
LC
M m v r m v
z1
z
1
a
C
b
z
2
J
z1
z2
J
z2
J M (a b)
2
?
J
z

M L 3
2
z
L
J
zc

M L 3
4M L 3
2
2

哈尔滨工业大学理论力学课后习题答案

哈尔滨工业大学理论力学课后习题答案

A
FAx
(a3)
FN1
A
P
1
B
FN3
P2
FN 2 (b1)
FN
B
FN3
P2
FN 2 (b3)
3
！！！！！！！！！！
理论力学（第七版）课后题答案 哈工大.高等教育出版社
(c)
FT
D FN2
B
P1
FN1 (c2)
FAy
A
FAx
C D FN2
B P1
P2
FN1 (c1) FAy
A
FAx
FT
P2 (c3)
x F1
O
40 F2
a F1
40

O
F2
b
FR
F3
F3
y
c
(a)
(b)
(c)
图 2-2
解 （1）解析法
建立如图 2-2b所示的直角坐标系 Oxy。
Fx F1 F2 cos402 000 N 2 500 Ncos40=3 915 N
！！！！！！！！！！
9
理论力学（第七版）课后题答案 哈工大.高等教育出版社
DE
D FAy
A
FAx
(k3)
！！！！！！！！！！
！！！！！！！！！！
6
理论力学（第七版）课后题答案 哈工大.高等教育出版社
FB
F1
B
F
B
B
！！！！！！！！！！
FD D
(l) FD D
A FA
(l1) F2
C FC (l2)
F1
F2
D
B
A
E
FE
FA

哈工大理力习题及习题答案

理论力学（I）第六版哈尔滨工业大学理论力学教研室第二章 平面汇交力系与平面力偶系2-1铆接薄板在孔心A 、B 和C 处受三力作用，如题2-1图（a ）所示。

F 1=100N ，沿铅直方向；F 3=50N ，沿水平方向，并通过点A ；F 2=50N ，力的作用线也通过点A ，尺寸如题2-1图(a)所示。

求此力系的合力。

解法一 几何法。

应用力的多边形法，将力F 1、F 2和F 3首尾相接后，再从F 1的起点至F 3的终点连一直线，此封闭边便是三力的合力F R ，如题2-1图（b ）所示。

根据预先选好的比例尺，利用直尺和量角器便可确定合力F R 的大小和方向。

解法二 解析法。

合力的矢量表达式为∑∑+=+=j F i F j F i F F y x Ry Rx R即合力R F 在x 轴和y 轴上的投影，分别等于力系各力在同一坐标轴上投影的代数和，所以有：N N F F F F xx x Rx 805080606050022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= N N F F F F yy y Rx 14008060805010022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= 所以，合力的大小为：N N F F F Ry Rx R2.161140802222=+=+=合力F R 与x 轴的夹角为：︒===24.602.16180arccos cosR Rx F F acr α 2-3物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在铰车D 上，如题2-3图（a ）所示。

转动铰车，物体便能升起。

设滑轮的大小、AB 与CB 杆自重及磨擦略去不计，A 、B 、C 三处均为铰链连接。

当物体处于平衡状态时，试求拉杆AB 和支杆CB 处受的力。

解：这是一个平面汇交力系的平衡问题。

选取滑轮B 为研究对象，并作B 点的受力图，如题2-3图（b ）所示。

由平衡方程∑∑==0,0y xF F，有：030sin 30cos =︒-︒+-T F F BC BA （1） 030cos 30sin =-︒-︒P T F BC （2）因忽略了滑轮B 的磨擦，所以P=T ，将P 、T 的数值代入（2）式，得KN F BC 64.74=将T 和F BC 的数值代入（1）式，得：kN F BA64.54=所以拉杆AB 和CB 分别受拉力54.64kN 和压力74.64kN 。

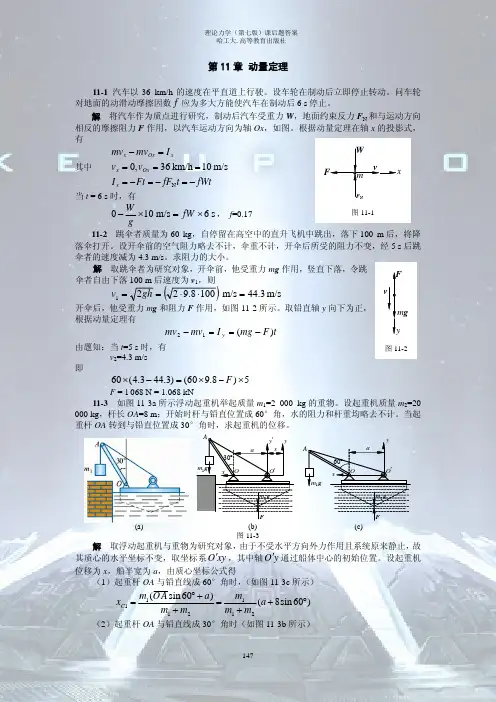
哈尔滨工业大学 第七版 理论力学11


上式代入式（4）得
FN = 4mB g − mB
11-10 如图 11-10a 所示，质量为 m 的滑块 A，可以在水平光滑槽中运动，具有刚性系 数为 k 的弹簧 1 端与滑块相连接，另 1 端固定。杆 AB 长度为 l，质量忽略不计，A 端与滑 块 A 铰接，B 端装有质量 m1，在铅直平面内可绕点 A 旋转。设在力偶 M 作用下转动角速度 ω 为常数。求滑块 A 的运动微分方程。
质量为 m2 的小车 D，由绞车拖动，相对于平台的运动规律为 s = 不计绞车的质量，求平台的加速度。
1 2 bt ，其中 b 为已知常数。 2
m2 g
y
S D
A
vr
m1 g FN
B
ω
v
(a) 图 11-8
x
(b)
解
受力和运动分析如图 11-8b 所示
& = bt vr = & s ar = & s& = b a Da = a e + a r = a AB + a r a Da = ar − a AB m2 (a r − a AB ) − m1a AB = F F = f (m1 + m2 ) g
1
(
)
开伞后，他受重力 mg 和阻力 F 作用，如图 11-2 所示。取铅直轴 y 向下为正， 根据动量定理有
mg y
图 11-2
mv 2 − mv1 = I y = (mg − F )t
由题知：当 t=5 s 时，有 v2=4.3 m/s 即
60 × (4.3 − 44.3) = (60 × 9.8 − F ) × 5
棱柱 B 接触水平面时系统质心坐标
a b ⎤ ⎡ m A (l − ) + m B ⎢l − (a − )⎥ 3 3 ⎦ 3(m A + m B )l − a (m A + 3m B ) + m B b ⎣ ′ = xC = m A + mB 3(m A + m B )

《理论力学》第十一章--动能定理试题及答案

理论力学12章作业题解12-2 弹簧原长为OA ，刚度系数为k ，O 端固定，A 端在半径为R 的圆弧上运动，求在由A 到B 及由B 到D 的过程中弹性力所作的功。

解 直接使用弹性力做功公式计算。

2222122211716.0])22(0[)(kR R R k k W B A B A -=--=-=®d d22022122210776.0 ])25.22cos 2()22[()(kRR R R R k k W D B D B =---=-=®d d12-5 AB 杆长80cm ，质量为2m ；OA 杆长40cm ，质量为m ，当AB 杆在水平位置时，两杆垂直，OA 杆的角速度s rad OA /32=w ，030=j 。

求此时系统的动能。

解 AB 杆平面运动的角速度为 s rad IA v A AB /138.04.032=´==w 其质心的速度为 s m IC v AB C /08.21)38.0(4.022=´+=´=w动能为m m m m J v m J T ABC C AB OA O 453.2 18.02 08.22)32()4.0( 221212121223121221221221=´´××+´×+´´×=++=w wICv Av CABw12-7 推土机前进速度为v 。

车架重G 1，两条履带各重G 2，四轮各重G 3，半径为R ，其惯性半径为r 。

求系统动能。

解 车架的动能：2112v gG T =履带的动能按质点系分析，其动能可分成两部分，即随质心平动的动能和相对于质心的动能。

履带质心速度为v ，各质点相对于质心的速度大小均为v 。

故其动能为：22222222)22(2v gG v g G v g G T =+= 轮子动能按平面运动刚体计算，轮心速度为v ，角速度R v /=w 。

哈工版理论力学教案11-2

上式在直角坐标轴上的投影式：，，即：质点对某定轴的动量矩对时间的一阶导数等于作用力对同一轴的矩3.5质点动量矩守恒定律若M O(F)≡0，则M O(mv)=恒量；若Mz(F)≡0，则Mz(mv)=恒量3.6质点系的动量矩定理因内力总是等值、反向、成对出现，所以上式右端第一项为0。

即：质点系对于某定点O的动量矩对时间的导数，等于作用于质点系的外力对于同一点的矩的矢量和。

即：质点系对于某定轴的动量矩对时间的导数，等于作用于质点系的外力对同一轴之矩的代数和。

3.7刚体绕定轴的转动微分方程根据质点系对定轴z的动量矩定理：因轴承约束力对z轴之矩为0，上式右边等于刚体主动力对该轴之矩的代数和。

∴∴或即：刚体对定轴转动惯量与角加速度的乘积，等于作用于刚体的主动力对该轴之矩的代数和。

()()FvxxMmMdtd=()()FvyyMmMdtd=()()FvzzMmMdtd=zF1F2F nAB()∑=eizz MdtdLF()()∑=FzzMJdtdω()∑=FzzMJα()∑=FzzMdtdJ22ϕ。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。