线性方程组有解的充要条件
- 格式:ppt
- 大小:209.00 KB
- 文档页数:2


线性代数知识点总结第一章 行列式二三阶行列式N 阶行列式:行列式中所有不同行、不同列的n 个元素的乘积的和n nn nj j j j j j j j j nij a a a a ...)1(21212121)..(∑-=τ(奇偶)排列、逆序数、对换行列式的性质:①行列式行列互换,其值不变。
(转置行列式T D D =) ②行列式中某两行(列)互换,行列式变号。
推论:若行列式中某两行(列)对应元素相等,则行列式等于零。
③常数k 乘以行列式的某一行(列),等于k 乘以此行列式。
推论:若行列式中两行(列)成比例,则行列式值为零; 推论:行列式中某一行(列)元素全为零,行列式为零。
④行列式具有分行(列)可加性⑤将行列式某一行(列)的k 倍加到另一行(列)上,值不变 行列式依行(列)展开:余子式ij M 、代数余子式ij j i ij M A +-=)1(定理:行列式中某一行的元素与另一行元素对应余子式乘积之和为零。
克莱姆法则:非齐次线性方程组 :当系数行列式0≠D 时,有唯一解:)21(n j DD x j j ⋯⋯==、齐次线性方程组 :当系数行列式01≠=D 时,则只有零解 逆否:若方程组存在非零解,则D 等于零 特殊行列式:①转置行列式:332313322212312111333231232221131211a a a a a a a a a a a a a a a a a a → ②对称行列式:ji ij a a =③反对称行列式:ji ij a a -= 奇数阶的反对称行列式值为零④三线性行列式:333122211312110a a a a a a a 方法:用221a k 把21a 化为零,。
化为三角形行列式 ⑤上(下)三角形行列式:行列式运算常用方法(主要)行列式定义法(二三阶或零元素多的) 化零法(比例)化三角形行列式法、降阶法、升阶法、归纳法、第二章 矩阵n *(零矩阵、负矩阵、行矩阵、列矩阵、n 阶方阵、相等矩阵) ---------交换、结合律 数乘n m ij ka kA *)(=---------分配、结合律乘法nm lkj ik n l kj l m ik b a b a B A *1**)()(*)(*∑==注意什么时候有意义一般AB=BA ,不满足消去律;由AB=0,不能得A=0或B=0 转置A A T T =)( TT T B A B A +=+)( T T kA kA =)( TT T A B AB =)((反序定理) 方幂:2121k k k kA AA +=2121)(k k k k A A +=对角矩阵:若AB 都是N 阶对角阵,k 是数,则kA 、A+B 、 数量矩阵:相当于一个数(若……)单位矩阵、上(下)三角形矩阵(若……) 对称矩阵 反对称矩阵阶梯型矩阵:每一非零行左数第一个非零元素所在列的下方 注:把分出来的小块矩阵看成是元素N 阶方阵,若存在N 阶矩阵B 的AB=BA=I 则称A 是可逆的,|A|=0、伴随矩阵)2.、非零k 乘某一行(列)3、将某行(列)的K 初等变换不改变矩阵的可逆性 初等矩阵都可逆倍乘阵 倍加阵) ⎪⎪⎭⎫ ⎝⎛=O OO I D rr矩阵的秩r(A):满秩矩阵 降秩矩阵 若A 可逆,则满秩 若A 是非奇异矩阵,则r (AB )=r (B ) 初等变换不改变矩阵的秩求法:1定义2转化为标准式或阶梯形矩阵与行列式的联系与区别:都是数表;行列式行数列数一样,矩阵不一样;行列式最终是一个数,只要值相等,就相等,矩阵是一个数表,对应元素相等才相等;矩阵n ij n ij a k ka )()(=,行列式nij n n ij a k ka =逆矩阵注:①AB=BA=I 则A 与B 一定是方阵 ②BA=AB=I 则A 与B 一定互逆; ③不是所有的方阵都存在逆矩阵;④若A 可逆,则其逆矩阵是唯一的。

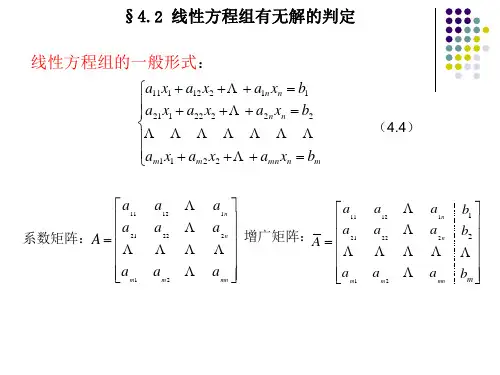
3.向量组的线性相关性与线性方程组的解§3.1 线性方程组解的判定1.定理3.1:n 元线性方程组AX=b ,其中A=(a 12a 12a 1n a 21a 22a 2na m1a m2a mn),x=( x 1x 2??x n ) ,b=( b 1b 2??b m )(1)无解的充要条件是R(A)<R(A,b);(2)有惟一解的充要条件是R(A)=R(A,b)=n ,(3)有无穷多解的充要条件是R(A)=R(A,b)<n.注:(1)R(A,b)先化为行阶梯形,判别。
有解时再化为行最简形求解。
(2)R(A)=m 时,AX=b 有解。
(3)R(A)=r 时,有n-r 个自由未知量,未必是后面n-r 个。
2.定理3.2:n 元线性方程组AX=0(1)有惟一解(只有零解)的充要条件是R(A)=n ; (2)有无穷多解(有非零解)充要条件是R(A)<n .注:(1)m <n,AX=0必有非零解。
3.定理3.3:矩阵方程AX=B 有解的充要条件是R(A)=R(A,B) 求解线性方程组例1. {4x 1+2x 2?x 3=23x 1?x 2+2x 3 =1011x 1+3x 2 =8例2. {2x 1+x 2?x 3+x 4 =14x 1+2x 2?2x 3+x 4=22x 1+x 2 ?x 3?x 4 =1例3. 求解齐次线性方程组{3x 1+ 4x 2?5x 3+ 7x 4 =02x 1?3x 2+3x 3? 2x 4 =04x 1+11x 2?13x 3+16x 4=07x 1?2x 2+ x 3+ 3x 4 =0例4.写出一个以X=C 1(2?310)+C 2(?2401)为通解的齐次线性方程组。
例5(每年).(1)λ取何值时,非齐次线性方程组{ λx 1+x 2+x 3=1x 1+λx 2+x 3=λx 1+x 2+λx 3=λ2(1)有惟一解;(2)无解;(3)有无穷多组解?并在有无穷多组解时求出通解.(2)非齐次线性方程组{x 1+x 2+2x 3=02x 1+x 2+ax 3=13x 1+2x 2+4x 3=b当a,b 取何值时,(1)有惟一解;(2)无解;(3)有无穷多组解?并求出通解.例5(12/13学年).设A=(λ110λ?1011λ), b=(a11),已知Ax=b 存在两个不同的解:(1)求λ,a;(2)求Ax=b 的通解。

一、行列式1.排列:由个不同数码1,2,……,组成的有序数组12……n。
2.逆序:在一个级排列12……n中,如果有较大的数t排在较小的数s前面,则称与构成一个逆序。
一个级排列中逆序的总数称为它的逆序数,逆序数是奇数称为奇排列,是偶数或0称为偶排列。
3.定理1:任意一个排列经过一个对换后奇偶性改变。
定理2:个数码(>1)共有!个级排列,其中奇偶排列各占一半。
4.用2个元素(=1,2, ……)组成的记号称为阶行列式,其中横排称为行,纵排称为列。
称为第行第列的元素,阶行列式表示所有可能取自不同的行,不同的列的个元素乘积的代数和,一般项可以写为其中12…n 构成一个级排列,当12…n取遍所有的级排列时,则得到阶行列式表示的代数和中所有的项。
5.主对角线:行列式中从左上角到右下角的对角线。
6.主对角线右上方元素全为0的行列式为下三角行列式,左下方元素全为0为上三角行列式,主对角线左上方和右上方元素全为0,主对角线上元素不全为0的行列式为对角行列式,它们的值均等于主对角线上元素的乘积。
7.行列式性质1 行列式转置,值不变,即D T=D8.性质2 交换行列式的两行(列),行列式的值变号,即D1=D。
9.性质3 用数乘行列式的某一行(列),等于数乘此行列式 ,即D1=D。
10.性质4 若将行列式中某一行(列)的每一个元素写成两个数的和,则此行列式可以写成两个行列式的和,这两个行列式分别以这两个数为所在行(列)对应位置的元素,其他位置的元素与原行列式相同,即D=D1+D211.推论:①若行列式中有两行(列)的对应元素相同,则此行列式值为0。
②若行列式中有两行(列)的对应元素成比例,则此行列式值为0。
③若行列式某行(列)的所有元素有公因子,则公因子可提到行列式外面。
④将行列式某一行(列)的所有元素同乘以数后加到另一行(列)对应位置的元素上,行列式值不变。
12.余子式M:在阶行列式D=||中去掉元素所在的第行第列后,余下的-1阶行列式。


线性代数知识点总结第一章 行列式二三阶行列式N 阶行列式:行列式中所有不同行、不同列的n 个元素的乘积的和n nn nj j j j j j j j j nij a a a a ...)1(21212121)..(∑-=τ(奇偶)排列、逆序数、对换行列式的性质:①行列式行列互换,其值不变。
(转置行列式T D D =) ②行列式中某两行(列)互换,行列式变号。
推论:若行列式中某两行(列)对应元素相等,则行列式等于零。
③常数k 乘以行列式的某一行(列),等于k 乘以此行列式。
推论:若行列式中两行(列)成比例,则行列式值为零; 推论:行列式中某一行(列)元素全为零,行列式为零。
④行列式具有分行(列)可加性⑤将行列式某一行(列)的k 倍加到另一行(列)上,值不变 行列式依行(列)展开:余子式ij M 、代数余子式ij j i ij M A +-=)1(定理:行列式中某一行的元素与另一行元素对应余子式乘积之和为零。
克莱姆法则:非齐次线性方程组 :当系数行列式0≠D 时,有唯一解:)21(n j DD x j j ⋯⋯==、齐次线性方程组 :当系数行列式01≠=D 时,则只有零解 逆否:若方程组存在非零解,则D 等于零 特殊行列式:①转置行列式:332313322212312111333231232221131211a a a a a a a a a a a a a a a a a a →②对称行列式:ji ij a a =③反对称行列式:ji ij a a -= 奇数阶的反对称行列式值为零④三线性行列式:333122211312110a a a a a a a 方法:用221a k 把21a 化为零,。
化为三角形行列式 ⑤上(下)三角形行列式:行列式运算常用方法(主要)行列式定义法(二三阶或零元素多的) 化零法(比例)化三角形行列式法、降阶法、升阶法、归纳法、第二章 矩阵n (零矩阵、负矩阵、行矩阵、列矩阵、n 阶方阵、相等矩阵) ---------交换、结合律 数乘n m ij ka kA *)(=---------分配、结合律乘法nm lkj ik n l kj l m ik b a b a B A *1**)()(*)(*∑==注意什么时候有意义一般AB=BA ,不满足消去律;由AB=0,不能得A=0或B=0 转置A A TT =)( TTTB A B A +=+)( TTkA kA =)( TTTA B AB =)((反序定理) 方幂:2121k k k kA AA +=2121)(k k k k A A +=对角矩阵:若AB 都是N 阶对角阵,k 是数,则kA 、A+B 、 数量矩阵:相当于一个数(若……)单位矩阵、上(下)三角形矩阵(若……) 对称矩阵 反对称矩阵阶梯型矩阵:每一非零行左数第一个非零元素所在列的下方 注:把分出来的小块矩阵看成是元素N 阶方阵,若存在N 阶矩阵B 的AB=BA=I 则称A 是可逆的,|A|=0、伴随矩阵)2.、非零k 乘某一行(列)3、将某行(列)的K 初等变换不改变矩阵的可逆性 初等矩阵都可逆倍乘阵 倍加阵) ⎪⎪⎭⎫ ⎝⎛=O OO I D rr矩阵的秩r(A):满秩矩阵 降秩矩阵 若A 可逆,则满秩 若A 是非奇异矩阵,则r (AB )=r (B ) 初等变换不改变矩阵的秩求法:1定义2转化为标准式或阶梯形矩阵与行列式的联系与区别:都是数表;行列式行数列数一样,矩阵不一样;行列式最终是一个数,只要值相等,就相等,矩阵是一个数表,对应元素相等才相等;矩阵n ij n ij a k ka )()(=,行列式nij n n ij a k ka =逆矩阵注:①AB=BA=I 则A 与B 一定是方阵 ②BA=AB=I 则A 与B 一定互逆; ③不是所有的方阵都存在逆矩阵;④若A 可逆,则其逆矩阵是唯一的。




线性代数模拟题一一填空题(每空3分,共30分)1、设 1231231232D a a ab b bc c c== 则213121321336322a a ab b bD c c c==2、设A 是3阶矩阵,且3,A =-则3A -=3、已知⎪⎪⎪⎭⎫ ⎝⎛-=-3211254321A ,则=--1)2(A4、设A 是45⨯矩阵,()2R A =.则线性方程组0AX =的基础解系含有 个解向量5、设1,2,3ηηη是非齐次线性方程组AX b =的解,若1122313ηληληη=++也是AX b =的解,则12λλ+=6、设),,(a 21=α,),,(01b =β,若α与β正交,则a 、b 所满足的关系为7、二次型()2221231231223,,246fx x x x x xx x x x =+---的矩阵A =8、设4阶方阵A 的特征值分别为1,2,3,2.-则A A +2的特征值为9、设157222203D = , 则313233A A A ++= 10、设()()1,2,1,1,3,2,1,1,22,αβγαβ=-=-+= 则γ=二 、计算行列式11111000000002211n n a a a a a a ---(10分) 三 、设301110,2014A AB A B ⎛⎫ ⎪==+ ⎪ ⎪⎝⎭. 求矩阵B .(12分)四、设向量组 ),,,,(432111-=α, ),,,,(1398732-=α, ),,,,(330313----=α, ),,,,(636914-=α ,求此向量组的秩及一个极大无关组,并将其余向量用该极大无关组线性表示.(14分)五、求下列非齐次线性方程组的一般解(12分)1234123412342132344352x x x x x x x x x x x x +-+=⎧⎪-+-=⎨⎪+-+=-⎩ 六、已知实对称矩阵⎪⎪⎪⎭⎫⎝⎛----=020212022A , 1.求A 的特征值与特征向量. 2.求一正交矩阵T ,使得1T AT -为对角阵.(16分) 七、设21λλ≠,且21λλ,为A 的特征值,21αα,为它们对应的特征向量,证明21αα,线性无关.(6分)线性代数模拟题二一. 填空题(每题3分,共30分)1. 设A 是3阶矩阵,且3,A =-则3A -=2. 设1,2,3ηηη是非齐次线性方程组A X b =的解,若1122313ηληληη=++也是A X b =的解,则12λλ+=3. 211132xx D x x=中x 的系数为 4. 设四元线性方程组AX b =的系数矩阵的秩为2,已知AX b =有解1,2,3,ηηη则AX b =的一般解为5. 设(1,1,0,2),(,1,1,1),k αβα=-=-与β正交,则k =6. 设二元方阵,A B 的逆分别是11532,,1414A B --⎛⎫⎛⎫==⎪ ⎪-⎝⎭⎝⎭则1()AB -= 7. 设3阶方阵A 的特征值为2,-1,3,则2A =8. 设A 为4⨯5矩阵,若A 的每个行向量都不能用其余的行向量来线性表示,则A 的秩为9. 设134213,473ij A A ⎛⎫ ⎪= ⎪ ⎪⎝⎭为A 中第I 行第j 列的元素的代数余子式,则21222334A A A ++=10. 二次型2221,23123121323(,)246f x x x x x x x x x x x x =++--+所对应的矩阵为二. 计算行列式 (10分)1234234134124123D =三.已知132301111A -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭,且2A AB E -=,求B (10分)四.求解方程组1234123412342132344352x x x x x x x x x x x x +-+=⎧⎪-+-=⎨⎪+-+=-⎩(12分)五.设向量组12345,,,,ααααα中12345(1,3,1,1),(1,7,3,9),(2,8,0,6),(3,9,3,3),(4,13,3,6)ααααα=-=----==-=-(1)求向量组的秩.(2)求向量组的一个极大无关组.(3)将其余向量用极大无关组线性表示 (14分)六.设A =124242421--⎛⎫ ⎪-- ⎪ ⎪--⎝⎭.(1)求A 的特征值.(2)求A 的特征向量(3)求正交矩阵T ,使得1T AT -为对角阵.(16分)七.证明:若非零向量β可由向量组12,,,m ααα 线性表示,且表达唯一,则12,,,m ααα 线性无关. (8分)线性代数模拟题三一、 判断题:(10分)1、两个n 维向量组等价当且仅当两个向量组的秩相等; ................. ( )2、两两正交的非零向量组一定是线性无关的向量组; ................... ( )3、矩阵A 、B 分别为线性方程组相应的系数矩阵和增广矩阵,则线性方程组有唯一解当且仅当R (A )=R (B ); .......................... ( )4、n 阶方阵A 的n 个特征值互不相等,则A 与对角阵相似; ............ ( )5、n 阶方阵A 与B 的特征值相同的充分必要条件是A 与B 相似。
n元齐次线性方程组有非零解的充要条件一、n元齐次线性方程组有非零解的充要条件齐次线性方程组有非零解的条件:在微分方程理论中,指x(t)≠0齐次线性方程组有非零解的条件。
一个齐次线性方程组有非零解的充分且必要条件是:它的系数矩阵的秩r小于它的未知量的个数n。
齐次线性方程组只有零解的条件:矩阵的秩=未知量的个数;系数矩阵列满秩;系数矩阵的列向量组线性无关,满足以上三个条件中的一个就只有零解。
二、定义常数项全为0的n元线性方程组称为n元齐次线性方程组。
设其系数矩阵为A,未知项为X,则其矩阵形式为AX=0。
若设其系数矩阵经过初等行变换所化到的行阶梯形矩阵的非零行行数为r,则它的方程组的解只有以下两种类型:1. 当r=n时,原方程组仅有零解;2. 当r<n时,有无穷多个解(从而有非零解)。
[3]三、证明对齐次线性方程组的系数矩阵施行初等行变换化为阶梯型矩阵后,不全为零的行数r(即矩阵的秩)小于等于m(矩阵的行数),若m<n,则一定n>r,则其对应的阶梯型n-r个自由变元,这个n-r个自由变元可取任意取值,从而原方程组有非零解(无穷多个解)。
示例依照定理n=4>m=3一定是存在非零解。
对系数矩阵施行初等行变换:最后一个矩阵为最简形,此系数矩阵的齐次线性方程组为:令X4为自由变元,X1,X2,X3为首项变元。
令X4=t,其中t为任意实数,原齐次线性方程组的解为四、判定定理定理1齐次线性方程组有非零解的充要条件是r(A)<n。
即系数矩阵A的秩小于未知量的个数。
推论齐次线性方程组仅有零解的充要条件是r(A)=n。
五、结构齐次线性方程组解的性质定理2:若x是齐次线性方程组的一个解,则kx也是它的解,其中k是任意常数。
定理3:若x1,x2是齐次线性方程组的两个解,则x1+x2也是它的解。
定理4:对齐次线性方程组,若r(A)=r<n,则存在基础解系,且基础解系所含向量的个数为n-r,即其解空间的维数为n-r。