幂的乘法、幂的乘方与积的乘方
- 格式:doc
- 大小:221.00 KB
- 文档页数:4

幂的运算1、同底数幂的乘法同底数幂相乘,底数不变,指数相加.公式表示为:()mnm na a am n +⋅=、为正整数同底数幂的乘法可推广到三个或三个以上的同底数幂相乘,即()m n p m m p a a a a m n p ++⋅⋅=、、为正整数注意:〔1〕同底数幂的乘法中,首先要找出一样的底数,运算时,底数不变,直接把指数相加,所得的和作为积的指数.〔2〕 在进展同底数幂的乘法运算时,如果底数不同,先设法将其转化为一样的底数,再按法那么进展计算.例1: 计算列以下各题 〔1〕 34a a ⋅; 〔2〕 23b b b ⋅⋅ ; 〔3〕 ()()()24c c c -⋅-⋅-练习:简单 一选择题1. 以下计算正确的选项是( )A.a2+a3=a5B.a2·a3=a5C.3m +2m =5mD.a2+a2=2a42. 以下计算错误的选项是( )A.5x2-x2=4x2B.am +am =2amC.3m +2m =5mD.x·x2m-1= x2m3. 以下四个算式中①a3·a3=2a3 ②x3+x3=x6 ③b3·b·b2=b5④p 2+p 2+p 2=3p 2正确的有( ) A.1个 B.2个 C.3个 D.4个4. 以下各题中,计算结果写成底数为10的幂的形式,其中正确的选项是( ) A.100×102=103 B.1000×1010=103C.100×103=105D.100×1000=104二、填空题1. a4·a4=_______;a4+a4=_______。
2、 b 2·b ·b 7=________。
3、103·_______=1010 4、(-a)2·(-a)3·a5=__________。
5、a5·a( )=a2·( ) 4=a186、(a+1)2·(1+a)·(a+1)5=__________。

辅导讲义)同底数幂:同底数幂是指底数相同的幂,如【注意】底数可以是具体的数,也可以是单项式或多项式.②不要把幂的乘方性质与同底数幂的乘法性质混淆,幂的乘方运算,是转化为指数的乘法运算(底数不变);同底数幂的乘法,是转化为指数的加法运算(底数不变). ③此性质可以逆用:()()nmmnm n a a a ==.如:()()533155222==知识点4.积的乘方指的是底数是乘积形式的乘方.如()3ab 、()2nab 等. 知识点5.积的乘方的法则积的乘方,等于把积中的每个因式分别乘方,再把所得的幂相乘. 这个性质适用于三个或三个以上因式的积的乘方.【注意】①公式中的n 可以是正整数,也可以是代表正整数的式子. a 与b 可以是数字,也可以是单项式或多项式.如()()()111,22mm mm m mab a b a b a b +++=+=+⎡⎤⎣⎦②注意积的乘方法则的结构:左边是幂的形式,而幂的底数是两个因数的积;右边是积,而积的因式时2个幂.③积中的每一个因数都应该乘方,不能遗漏.④注意法则的准确应用,不能随便模仿.如,()222ab a b =是正确的,但()222a b a b +=+是错误的.⑤此性质可以逆用,即()nn na b ab =,在计算中若有指数相同的幂相乘,可先把底数相乘,在去求积的同次幂.有时候性质的逆向适用,会使一些数的计算简化.如,2006200620061122122⎛⎫⎛⎫=⨯= ⎪⎪⎝⎭⎝⎭知识点6.关于幂的三种运算(同底数幂相乘、幂的乘方、积的乘方)法则的异同归纳如下【典型例题讲解】x x = 23111010⎫⎛⎫⨯⎪ ⎪⎭⎝⎭()n m n -=; B. ()n m n ⎤-=⎥⎦;)()23298mn m n -=-; D. ()3299mn m n -=.-;+;a a ax x x-.++;(x x xa a a a a)()()--;)()()a a--;x x)()b a-;a b-;()()++;n m m n2b a-;()()()()m n m n --; )()()()a b b a a b ----.。

同底数幂的乘法: 1、表示的意义是a5‗‗‗‗‗‗ ;a n的意义是n 个a ‗‗‗‗‗‗,我们把这种运算叫做‗‗‗‗‗‗,乘方的结果叫‗‗‗‗,a 叫做‗‗‗‗‗‗‗‗,n 是‗‗‗‗‗‗‗.)(2a -底数为‗‗‗‗‗,指数为‗‗‗‗‗;a2底数为‗‗‗‗‗,指数为‗‗‗‗‗;)(3y x -底数为‗‗‗‗‗‗‗‗,指数为‗‗‗‗‗;)(y x n-底数为‗‗‗‗‗‗‗‗,指数为‗‗‗‗‗.2、根据乘方的意义可知:1010315⨯=(10×…×10)×(10×10×10)=10×10×…×10=10 一般的,对于任意底数a 与任意正整数m ,n,.)()(nm +=⋅⋯⋅⋅=⋅⋯⋅⋅⋅⋅⋯⋅⋅=⋅a a a a a a a a a a a anm因此,我们有.(都是正整数),n m aa anm nm+=⋅即同底数幂相乘,底数‗‗‗‗‗,指数‗‗‗‗‗. 3、计算=⋅22n m‗‗‗‗‗‗‗;=⋅-22510‗‗‗‗‗‗;=⋅⋅x x x nm ‗‗‗‗‗‗;=⨯⨯-)()(2-2-)2(34‗‗‗‗‗;=⋅-xx n n223‗‗‗‗‗‗‗;)(2)(y x y x -⋅--=‗‗‗‗‗‗同底数相乘,底数不变,指数相加,当三个或三个以上的同底数幂相乘时,法则也适用. 同底数幂相乘时,底数可以是单项式,也可以是多项式.在幂的运算中,经常用到以下变形:⎪⎩⎪⎨⎧=--为奇数)为偶数)n a a a nn n(n ()( ⎪⎩⎪⎨⎧=----为奇数)为偶数)n n a b a b b a nnn (()()()( 4、计算:(1)=⋅⋅----)()()(32x y x y y x ‗‗‗‗‗‗‗‗;(2)===+333ba 8,6,则ba(3)===+aa annm ,7,6则吗‗‗‗‗‗‗‗‗;(4)若==+2233x x 则‗‗‗‗‗‗‗‗;(5)若==+aa m m13,则‗‗‗‗‗‗‗‗;5、已知xn 1-( )=xmn +,则在括号内应填上( ).A 、xmB 、xm 1-C 、xm 1+ D 、xm 2+6、若的值是则a a a nnm m,15,3==+( ).A 、2 B 、3 C 、4 D 、57、若等于则x x ,3222=+( )A 、1 B 、2 C 、3 D 、48、若,2738112+=⨯x 则x 2的值是( )A 、4 B 、7 C 、9 D 、19、若b b ba aan n n m 8225121,=⋅=⋅+-+,则m+n 的值是‗‗‗‗‗‗‗.10、计算下列各题。
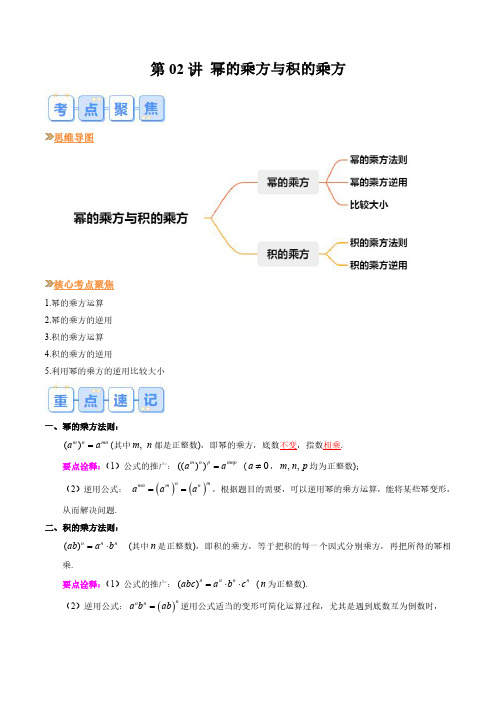

第三十五讲 幂的乘方与积的乘方【知识要点】一、幂的乘方:①幂的乘方法则:底数不变,指数相乘,()m n mn a a=(m 、n 都是正整数) ②公式逆用:()()mn m n n m a a a ==③多重乘方:()(p n m mnp a a m ⎡⎤=⎢⎥⎣⎦、n 、p 都是正整数) 二、积的乘方:①积的乘方法则:积的乘方等于每一个因数乘方的积,()m m m ab a b =⋅(m 为正整数) ②三个或三个以上的数的积的乘方也具有这一性质,()n n n n abc a b c = ③积的乘方法则也可以逆用.即(),()m m m n n n n ab ab a bc abc ⋅==三、注意: ①幂的乘方要和同底数幂的乘法区别开来;②积的乘方等于将积的每个因式分别乘方(即转化成若干个幂的乘方),再把所得的幂相乘.【经典例题】【例1】计算.①5324)()(x x x -⋅-⋅ ②m m m x x x 5233)()(⋅⋅+ ③3342])([b a a -⋅-④2333)105.2()104.0(⨯⨯⨯ ⑤24232)3(3)2(a a a -⋅-【例2】已知:625255=⋅x x ,求x 的值.【例3】若63=a ,5027=b ,求a b +33的值.【例4】已知192221232=-++a a ,求a 的值.【例5】比较5553,4444,3335的大小.【初试锋芒】1.计算:①432)3(b a --= ; ②3243)()(a a -⋅-= ; ③=⨯-20152014)522()125( ; ④323)21(bc a -= ; ⑤2009200822-= ; ⑥()n m a a ⋅3=2.若5,2n n a b ==则32()n a b = ; n 为奇数,则22()()n n a a -+-= .3.下列运算正确的是( )4.计算32)2(xy --,结果正确的是( ) A. 5361y x B. 6381y x - C. 6361y x - D. 5381y x - 5.下列计算:(1)22)(m m a a-=;(2)m m a a )(22-=;(3)743222)()(b a b a ab =-⋅-;(4)212218)3()2(++=-⋅n n n n b ab a ab ;(5)52236)3(b a ab =中正确的个数为( )6.已知m x =10,n y =10,则m y x =+3210等于( ) A. n m 32+ B. 22n m + C. mn 6 D. 32n m7.下列四个式子中结果为1210的有( )①661010+; ②21010)52(⨯; ③6510)1052(⨯⨯⨯; ④43)10( A. ①② B. ③④ C. ②③ D. ①④8.如果正方体的棱长是3)2-1(b ,那么这个正方体的体积是( )A. 6)2-1(bB. 9)2-1(bC. 12)2-1(bD. 6)2-1(6b9.n m 279⋅等于( )A. n m +9B. n m +27C. n m 323+D. n m 933+ 10.已知3181=a ,4127=b ,519=c ,则a ,b ,c 的大小关系是( )【大展身手】1.计算:①201410078)125.0(⨯- ②b a ab b a a ⋅-⋅-+⋅-⋅-32332)()3()2()()(2.①若62=m ,34=n ,求3222++n m 的值.②3,4m na a ==求32m n a +的值为多少?3.已知17232793=⨯⨯m m ,求m 的值.4.若0542=-+y x ,求y x 164⋅的值.【挑战脑细胞】1.设112233445,4,3,2====D C B A ,则A 、B 、C 、D 从小到大的排列顺序是怎样的?2.已知:m n +3能被13整除,求证:m n ++33也能被13整除.。

幂的乘方运算法则
底数不变,指数相乘。
即
a的m次幂的n次幂=a的(m?n)次幂(n、m为正整数)
积的乘方运算法则
把积的每个因式分别乘方,再把所得的幂相乘。
即
a、b乘积的n次方=a的n次方乘b的n次方(n为正整数)
幂的乘方与积的乘方运算法则
幂的乘方法则:幂的乘方是幂的一种运算积的乘方是指底数是乘积形式的乘方。
积的乘方法则:积的乘方,先把积中的每一个因数分别乘方,再把所得的幂相乘。
幂的乘方最终转化为指数的乘法运算,其中底数a可以是具体的数、单项式、多项式、分式乃至任何代数式。
幂的乘方是类比数的乘方,并借助于同底数幂的乘法性质来学习的,首先在具体例子的基础上抽象出幂的乘方的性质,进而通过推理加以论证,这一过程蕴含着转化及由特殊到一般,从具体到抽象的数学思想方法
幂的乘方与积的乘方运算法则
幂的乘方的运算法则:幂的乘方,低数不变,指数相加。
积的乘方的运算法则:是指底数是乘积形式的乘方。
幂的运算一1.同底数幂的乘法:a m·a n=a m+n (m, n是自然数)同底数幂的乘法法则是本章中的第一个幂的运算法则,也是整式乘法的主要依据之一。
学习这个法则时应注意以下几个问题:(1)先弄清楚底数、指数、幂这三个基本概念的涵义。
(2)它的前提是“同底”,而且底可以是一个具体的数或字母,也可以是一个单项式或多项式,如:(2x+y)2·(2x+y)3=(2x+y)5,底数就是一个二项式(2x+y)。
(3)指数都是正整数(4)这个法则可以推广到三个或三个以上的同底数幂相乘,即a m·a n·a p....=a m+n+p+... (m, n, p都是自然数)。
(5)不要与整式加法相混淆。
乘法是只要求底数相同则可用法则计算,即底数不变指数相加,如:x5·x4=x5+4=x9;而加法法则要求两个相同;底数相同且指数也必须相同,实际上是幂相同系数相加,如-2x5+x5=(-2+1)x5=-x5,而x5+x4就不能合并。
例1.计算:(1) (- )(- )2(- )3 (2) -a4·(-a)3·(-a)5解:(1) (- )(- )2(- )3分析:①(- )就是(- )1,指数为1=(- )1+2+3②底数为- ,不变。
=(- )6③指数相加1+2+3=6= ④乘方时先定符号“+”,再计算的6次幂解:(2) -a4·(-a)3·(-a)5分析:①-a4与(-a)3不是同底数幂=-(-a)4·(-a)3·(-a)5可利用-(-a)4=-a4变为同底数幂=-(-a)4+3+5②本题也可作如下处理:=-(-a)12-a4·(-a)3·(-a)5=-a4(-a3)(-a5)=-a12=-(a4·a3·a5)=-a12例2.计算(1) (x-y)3(y-x)(y-x)6解:(x-y)3(y-x)(y-x)6分析:(x-y)3与(y-x)不是同底数幂=-(x-y)3(x-y)(x-y)6 可利用y-x=-(x-y), (y-x)6=(x-y)6=-(x-y)3+1+6变为(x-y)为底的同底数幂,再进行计算。