下载文档原格式
第七章回归与相关分析一、填空题1．现象之间的相关关系按相关的程度分为、和；按相关的形式分为和；按影响因素的多少分为和。
2．两个相关现象之间，当一个现象的数量由小变大，另一个现象的数量，这种相关称为正相关；当一个现象的数量由小变大，另一个现象的数量，这种相关称为负相关。
3．相关系数的取值X围是。
4．完全相关即是关系，其相关系数为。
5．相关系数，用于反映条件下，两变量相关关系的密切程度和方向的统计指标。
6．直线相关系数等于零，说明两变量之间；直线相关系数等1，说明两变量之间；直线相关系数等于—1，说明两变量之间。
7．对现象之间变量的研究，统计是从两个方面进行的，一方面是研究变量之间关系的，这种研究称为相关关系；另一方面是研究关于自变量和因变量之间的变动关系，用数学方程式表达，称为。
8．回归方程y=a+bx中的参数a是，b是。
在统计中估计待定参数的常用方法是。
9. 分析要确定哪个是自变量哪个是因变量，在这点上它与不同。
10．求两个变量之间非线性关系的回归线比较复杂，在许多情况下，非线性回归问题可以通过化成来解决。
11．用来说明回归方程代表性大小的统计分析指标是。
12．判断一条回归直线与样本观测值拟合程度好坏的指标是。
二、单项选择题1．下面的函数关系是( )A销售人员测验成绩与销售额大小的关系 B圆周的长度决定于它的半径C家庭的收入和消费的关系 D数学成绩与统计学成绩的关系2．相关系数r的取值X围( )A -∞<r<+∞B -1≤r≤+1C -1<r<+1D 0≤r≤+13．年劳动生产率z(干元)和工人工资y=10+70x，这意味着年劳动生产率每提高1千元时，工人工资平均( )A增加70元 B减少70元 C增加80元 D减少80元4．若要证明两变量之间线性相关程度是高的，则计算出的相关系数应接近于( )A+1 B 0 C 0．5 D [1]5．回归系数和相关系数的符号是一致的，其符号均可用来判断现象( ) A线性相关还是非线性相关 B正相关还是负相关C完全相关还是不完全相关 D单相关还是复相关6．某校经济管理类的学生学习统计学的时间(x)与考试成绩(y)之间建=a+b x。
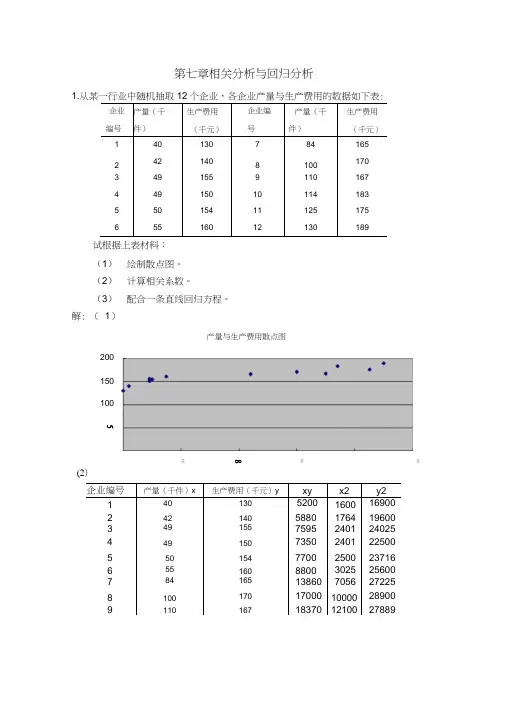
第七章相关分析与回归分析1.企业 编号 产量（千 件）生产费用 （千元）企业编 号 产量（千 件）生产费用 （千元） 1 40 130 7 84 165 2 42 140 8 100 170 3 49 155 9 110 167 4 49 150 10 114 183 550 154 11 125 175 65516012130189试根据上表材料： （1） 绘制散点图。
（2） 计算相关系数。
（3） 配合一条直线回归方程。
解: （ 1）(2) 企业编号产量（千件）x生产费用（千元）yxy x2 y2 1 40 130 **** **** 16900 2 42 140 5880 1764 19600 3 49 155 **** **** 24025 4 49 150 **** **** 22500 5 50 154 7700 2500 23716 6 55 160 8800 3025 25600 784 165 138607056272258 100170 17000 10000 28900 911016718370 12100 278896080040200 150 100产量与生产费用散点图512x159062 -948x1938.12 88368 -9482、12 316190 -19382(3)设回归方程为? = a bxb』甞7n Z x 一(送 x)12 159062-948 1938 12y -bx =1^ -0.4423948=126.558312 12所以回归方程为$ =126.5583 0.4423x2.某县城研究居民月家庭人均生活费支出和月家庭收入的相互关系，随机抽样 10利用上表材料：(1) 绘制散点图并观察两变量之间是否存在线性关系 (2) 计算相关系数，建立回归方程。
(3) 计算估计标准误差。
(4) 测算人均收入为200时，其人均生活费应为多少元 解: ( 1)12 88368-9482_ n 瓦xy-任x)任y) n' x 2 -r x)2. n' y 2 -(' y)2 71520 78838.84-0.907271520 161712二 0.4423(2) 家庭序号月人均收入（元）x月人均生活费（元）yxy x2y21 100 85 8500 10000 72252 110 88 968012100 77443 120 90 10800 14400 81004 130 94 12220 16900 88365 140 96 13440 19600 9216 6 150 100 15000 22500 100007 160 106 16960 25600 112368 170 118 20060 28900 13924 9180 120 21600 32400 14400 10 190 124 23560 36100 15376合计14501021151820 218500 106057n' xy-C x)(' y)10 151820 -1450 1021设回归方程为bxn £ xy-(£ x)(£ y) 10 汇 151820 —1450 乂 1021 n' x 2-C x)2 n' y 2-(' y)2 _ 10 218500 -14502a-bx=1021-0.45761450=35.74810 10所以回归方程为? =35.748 0.4576x (3)、10 218500 -14502 一 10 106057 -10212费活生均人月200-C x)2 .. n'y 2-c y)2 3775038673.54= 0.97613775082500 = 0.4576月人均生活费与人均收入散点图120140160月人均收入180oo oooooo 4 2 0 8 6 4 2' y2-a' y-b' xy _ 106057-35.748 1021-0.4576 151820 目二n-2 「10-2= 3.2684(4)当x=200 时，人均生活费为：y =35.748 0.4576 200 =127.2683. 已知x、y两变量的相关系数r = 0.8 , X =20, y = 50,二y为二x的两倍，求y 对x 的回归方程。
第七章回归分析前几章所讨论的内容，其目的在于寻求被测量的最佳值及其精度。
在生产和科学实验中，还有另一类问题，即测量与数据处理的目的并不在于获得被测量的估计值，而是为了寻求两个变量或多个变量之间的内在关系，这就是本章所要解决的主要问题。
表达变量之间关系的方法有散点图、表格、曲线、数学表达式等，其中数学表达式能较客观地反映事物的内在规律性，形式紧凑，且便于从理论上作进一步分析研究，对认识自然界量与量之间关系有着重要意义。
而数学表达式的获得是通过回归分析方法完成的。
第一节回归分析的基本概念一、函数与相关在生产和科学实验中，人们常遇到各种变量。
从贬值辩证唯物主义观点来看，这些变量之间是相互联系、互相依存的，它们之间存在着一定的关系。
人们通过实践，发现变量之间的关系可分为两种类型：1.函数关系（即确定性关系）数学分析和物理学中的大多数公式属于这种类型。
如以速度v作匀速运动的物体，走过的距离s与时间t之间，有如下确定的函数关系：s=vt若上式中的变量有两个已知，则另一个就可由函数关系精确地求出。
2.相关关系在实际问题中，绝大多数情况下变量之间的关系不那么简单。
例如，在车床上加工零件，零件的加工误差与零件的直径之间有一定的关系，知道了零件直径可大致估计其加工误差，但又不能精确地预知加工误差。
这是由于零件在加工过程中影响加工误差的因素很多，如毛坯的裕量、材料性能、背吃刀量、进给量、切削速度、零件长度等等，相互构成一个很复杂的关系，加工误差并不由零件直径这一因素所确定。
像这种关系，在实践中是大量存在的，如材料的抗拉强度与其硬度之间；螺纹零件中螺纹的作用中径与螺纹中径之间；齿轮各种综合误差与有关单项误差之间；某些光学仪器、电子仪器等开机后仪器的读数变化与时间之间；材料的性能与其化学成分之间等等。
这些变量之间既存在着密切的关系，又不能由一个（或几个）变量（自变量）的数值精确地求出另一个变量（因变量）的数值，而是要通过试验和调查研究，才能确定它们之间的关系，我们称这类变量之间的关系为相关关系。
第七章 相关与回归分析（一）填空题1、相关关系按其相关的程度不同，可分为 、 和 。
2、相关系数的正负表示相关关系的方向，r 为正值，两变量是 ；r 为负数，两变量是 。
3、r=0，说明两个变量之间 ；r=+1，说明两个变量之间 ；r=-1说明两个变量之间 。
4、一元线性回归方程bx a y+=ˆ 中的参数a 代表 ，数学上称为 ；b 代表 ，数学上称为 。
5、 分析要根据研究的目的确定哪一个为自变量，哪一个为因变量，在这一点与 分析时不同。
6、相关关系按方向不同，可分为 和 。
7、完全线性相关的相关系数r 值等于 。
8、计算回归方程要注意资料中因变量是 的，自变量是 的。
9、回归方程只能用于由 推算 。
（二）单项选择题（在每小题备选答案中，选出一个正确答案）1、相关分析研究的是( )A. 变量之间关系的密切程度B. 变量之间的因果关系C. 变量之间严格的相互依存关系D. 变量之间的线性关系2、相关关系是（ ）A 、现象间客观存在的依存关系B 、现象间的一种非确定性的数量关系C 、现象间的一种确定性的数量关系D 、现象间存在的函数关系3、下列情形中称为正相关的是( )A. 随着一个变量的增加，另一个变量也增加B. 随着一个变量的减少，另一个变量增加C. 随着一个变量的增加，另一个变量减少D. 两个变量无关4、当自变量x 的值增加，因变量y 的值也随之增加，两变量之间存在着（ ）A 、曲线相关B 、正相关C 、负相关D 、无相关5、相关系数r 的取值范围是( )A. B.C. 6、当自变量x 的值增加，因变量y 的值也随之减少，两变量之间存在着（ ）A 、曲线相关B 、正相关C 、负相关D 、无相关7、相关系数等于零表明两变量( )A. 是严格的函数关系B. 不存在相关关系C. 不存在线性相关关系D. 存在曲线相关关系8、相关系数r 的取值范围是（ ）A 、从0到1B 、从-1到0C 、从-1到1D 、无范围限制11<<-r 10≤≤r 11≤≤-r9、相关分析对资料的要求是( )A. 两变量均为随机的B. 两变量均不是随机的C. 自变量是随机的，因变量不是随机的D. 自变量不是随机的，因变量是随机的10、相关分析与回归分析相比，对变量的性质要求是不同的，回归分析中要求（ ）A 、自变量是给定的，因变量是随机的B 、两个变量都是随机的C 、两个变量都是非随机的D 、因变量是给定的，自变量是随机的11、回归方程 中的回归系数b说明自变量变动一个单位时，因变量( )A. 变动b个单位 B. 平均变动b 个单位C.变动a+b 个单位 D. 变动a 个单位12、一般来说，当居民收入减少时，居民储蓄存款也会相应减少，二者之间的关系是（ ）A 、负相关B 、正相关C 、零相关D 曲线相关13、回归系数与相关系数的符号是一致的，其符号均可判断现象( )A. 线性相关还是非线性相关B. 正相关还是负相关C. 完全相关还是不完全相关D. 简单相关还是复相关14、配合回归方程比较合理的方法是（ ）A 、移动平均法B 、半数平均法C 、散点法D 、最小平方法15、在相关分析中不能把两个变量区分为确定性的自变量和随机性的因变量，在回归分析中( )A. 也不能区分自变量和因变量B. 必须区分自变量和因变量C. 能区分，但不重要D. 可以区分，也可以不区分16、价格愈低，商品需求量愈大，这两者之间的关系是（ ）A 、复相关B 、不相关C 、正相关D 、负相关17、按最小平方法估计回归方程 中参数的实质是使( )A. B. C. D. 18、判断现象之间相关关系密切程度的方法是（ ）A 、作定性分析B 、制作相关图C 、计算相关系数D 、计算回归系数19、在线性相关条件下，自变量的标准差为2，因变量的标准差为5，而相关系数为0.8，其回归系数为( )A. 8B. 12.5C. 0.32D. 2.020、已知某产品产量与生产成本有直线关系，在这条直线上，当产量为1000件时，其生产成本为50000元，其中不随产量变化的成本为12000元，则成本总额对产量的回归方程是（ ）A 、Y=12000+38XB 、Y=50000+12000XC 、Y=38000+12XD 、Y=12000+50000Xbx a y +=ˆbx a y +=ˆ∑=-最小值2)ˆ(y y21、已知，则相关系数为()A.不能计算 22、相关图又称（ ）A 、散布表B 、折线图C 、散点图D 、曲线图23、工人的出勤率与产品合格率之间的相关系数如果等于0.85，可以断定两者是（ ）A 、显著相关B 、高度相关C 、正相关D 、负相关24、相关分析与回归分析的一个重要区别是（ ）A 、前者研究变量之间的关系程度，后者研究变量间的变动关系，并用方程式表示B 、前者研究变量之间的变动关系，后者研究变量间的密切程度C 、两者都研究变量间的变动关系D 、两者都不研究变量间的变动关系25、当所有观测值都落在回归直线上，则这两个变量之间的相关系数为（ ）A 、1B 、-1C 、+1或-1D 、大于-1，小于+126、一元线性回归方程y=a+bx 中，b 表示（ ）A 、自变量x 每增加一个单位，因变量y 增加的数量B 、自变量x 每增加一个单位，因变量y 平均增加或减少的数量C 、自变量x 每减少一个单位，因变量y 减少的数量D 、自变量x 每减少一个单位，因变量y 增加的数量（三）多项选择题（在每小题备选答案中，至少有两个答案是正确的）1、直线回归方程 中，两个变量x 和y ( )A. 前一个是自变量 ，后一个是因变量B. 两个变量都是随机变量C. 两个都是给定的量D. 前一个是给定的量 ，后一个是随机变量E. 前一个随机变量 ，后一个是给定的量2、相关分析（ ）A 、分析对象是相关关系B 、分析方法是配合回归方程C 、分析方法主要是绘制相关图和计算相关系数D 、分析目的是确定自变量和因变量E 、分析目的是判断现象之间相关的密切程度，并配合相应的回归方程以便进行推算和预测3、相关分析的特点有 ( )A. 两个变量是对等的关系B. 它只反映自变量和因变量的关系C. 可以计算出两个相关系数D. 相关系数的符号都是正的E. 相关的两个变量必须都是随机的4、下列现象中存在相关关系的有（ ）A 、职工家庭收入不断增长，消费支出也相应增长B 、产量大幅度增加，单位成本相应下降C 、税率一定，纳税额随销售收入增加而增加D 、商品价格一定，销售额随销量增加而增加E 、农作物收获率随着耕作深度的加深而提高bx a y +=ˆ5、相关关系与函数关系的区别在于( )A. 相关关系是变量间存在相互存在依存关系，而且函数关系是因果关系B. 相关关系的变量间是确定不变的，而函数关系值是变化的C. 相关关系是模糊的，函数关系是确定的D. 两种关系没有区别6、商品流通费用率与商品销售额之间的关系是（ ）A 、相关关系B 、函数关系C 、正相关D 、负相关E 、单相关7、为了揭示变量x 与y 之间的相互关系，可运用( )A. 相关表B. 回归方程C.相关系数D. 散点图8、相关系数（ ）A 、是测定两个变量间有无相关关系的指标B 、是在线性相关条件下测定两个变量间相关关系密切程度的指标C 、也能表明变量之间相关的方向D 、其数值大小决定有无必要配合回归方程E 、与回归系数密切相关9、可以借助回归系数来确定( )A. 两变量之间的数量因果关系B. 两变量之间的相关方向C. 两变量之间的相关的密切程度D.10、直线回归方程（ ）A、建立前提条件是现象之间具有较密切的直线相关关系B 、关键在于确定方程中的参数a 和bC 、表明两个相关变量间的数量变动关系D 、可用来根据自变量值推算因变量值，并可进行回归预测E 、回归系数b=0时，相关系数r=011、可用来判断现象相关方向的指标有( )A. 相关系数B. 回归系数C. 回归参数aD. 协方差E. 估计标准误差 12、某种产品的单位成本y （元）与工人劳动生产率x （件/人）之间的回归直线方程Y=50-0.5X ，则（ ）A 、0.5为回归系数B 、50为回归直线的起点值C 、表明工人劳动生产率每增加1件/人，单位成本平均提高0.5元D 、表明工人劳动生产率每增加1件/人，单位成本平均下降0.5元E 、表明工人劳动生产率每减少1件/人，单位成本平均提高50元13、对于回归系数，下列说法中正确的有( )A. b 是回归直线的斜率B. b 的绝对值介于0-1之间C. bD. bE. b 满足方程组y S ⎪⎩⎪⎨⎧+=+=∑∑∑∑∑2xb x a xy x b na y14、相关关系的特点是（）A、现象之间确实存在数量上的依存关系B、现象之间不确定存在数量上的依存关系C、现象之间的数量依存关系值是不确定的D、现象之间的数量依存关系值是确定的E、现象之间不存在数量上的依存关系15、回归方程可用于( )A. 根据自变量预测因变量B. 给定因变量推算自变量C. 给定自变量推算因变量D. 推算时间数列中缺失的数据E. 用于控制因变量16、建立一元线性回归方程是为了（）A、说明变量之间的数量变动关系B、通过给定自变量数值来估计因变量的可能值C、确定两个变量间的相关程度D、用两个变量相互推算E、用给定的因变量数值推算自变量的可能值17、在直线回归方程中，两个变量x和y（）A、一个是自变量，一个是因变量B、一个是给定的变量，一个是随机变量C、两个都是随机变量D、两个都是给定的变量E、两个是相关的变量18、在直线回归方程中（）A、在两个变量中须确定自变量和因变量B、回归系数只能取正值C、回归系数和相关系数的符号是一致的D、要求两个变量都是随机的E、要求因变量是随机的，而自变量是给定的19、现象间的相关关系按相关形式分为（）A、正相关B、负相关C、直线相关D、曲线相关E、不相关20、配合一元线性回归方程须具备下列前提条件（）A、现象间确实存在数量上的相互依存关系B、现象间的关系是直线关系，这种直线关系可用散点图来表示C、具备一组自变量与因变量的对应资料，且能明确哪个是自变量，哪个是因变量D、两个变量之间不是对等关系E、自变量是随机的，因变量是给定的值21、由直线回归方程y=a+bx所推算出来的y值（）A、是一组估计值B、是一组平均值C、是一个等差级数D、可能等于实际值E、与实际值的离差平方和等于0（四）是非题1、判断现象之间是否存在相关关系必须计算相关系数。
第七章相关与回归分析学习内容一、变量间的相关关系二、一元线性回归三、线性回归方程拟合优度的测定学习目标1. 掌握相关系数的含义、计算方法和应用2. 掌握一元线性回归的基本原理和参数的最小二3. 掌握回归方程的显著性检验4. 利用回归方程进行预测5. 了解可化为线性回归的曲线回归6. 用Excel 进行回归分析一、变量间的相关关系1. 变量间的关系（函数关系）1)是一一对应的确定关系。
2)设有两个变量x和y，变量y 随变量x一起变化，并完全依赖于x，当变量x 取某个数值时，y依确定的关系取相应的值，则称y 是x的函数，记为y = f (x)，其中x 称为自变量，y 称为因变量。
3)各观测点落在一条线上。
4）函数关系的例子–某种商品的销售额(y)与销售量(x)之间的关系可表示为 y = p x (p 为单价)。
–圆的面积(S)与半径之间的关系可表示为S = π R2。
–企业的原材料消耗额(y)与产量x1、单位产量消耗x2、原材料价格x3间的关系可表示为y =x1 x2 x3。
单选题下面的函数关系是（）A、销售人员测验成绩与销售额大小的关系B、圆周的长度决定于它的半径C、家庭的收入和消费的关系D、数学成绩与统计学成绩的关系2. 变量间的关系（相关关系）1)变量间关系不能用函数关系精确表达。
2)一个变量的取值不能由另一个变量唯一确定。
3)当变量 x 取某个值时，变量 y 的取值可能有几个。
4)各观测点分布在直线周围。
5）相关关系的例子–商品的消费量(y)与居民收入(x)之间的关系。
–商品销售额(y)与广告费支出(x)之间的关系。
–粮食亩产量(y)与施肥量(x1)、降雨量(x2)、温度 (x3)之间的关系。
–收入水平(y)与受教育程度(x)之间的关系。
–父亲身高(y)与子女身高(x)之间的关系。
3. 相关图表1)相关表：将具有相关关系的原始数据，按某一顺序平行排列在一张表上，以观察它们之间的相互关系。
2)相关图：也称为分布图或散点图，它是在平面直角坐标中把相关关系的原始数据用点描绘出来，通常以直角坐标轴的横轴代表自变量x，纵轴代表因变量y。
4. 相关关系的类型相关关系的图示（散点图）5. 相关关系的测度（相关系数）1)对变量之间关系密切程度的度量。
2)对两个变量之间线性相关程度的度量称为简单相关系数。
3)若相关系数是根据总体全部数据计算的，称为总体相关系数，记为ρ。
4)若是根据样本数据计算的，则称为样本相关系数，记为 r。
样本相关系数的计算公式化简为相关系数取值及其意义a)r 的取值范围是 [-1,1]。
|r|=1，为完全相关。
(r =1，为完全正相关。
r =-1，为完全负相关。
)b)r = 0，不存在线性相关关系。
c)-1<r<0，为负相关。
d)0<r<1，为正相关。
e) |r|越趋于1表示关系越密切；|r|越趋于0表示关系越不密切。
单选题①下列哪两个变量之间的相关程度高（）– A、商品销售额和商品销售量的相关系数是0.9– B、商品销售额和商业利润率的相关系数是0.84– C、平均流通费用率与商业利润率的相关系数是0.94– D、商品销售价格与销售量的相关系数是-0.91②下列关系中，属于正相关关系的有（）– A、合理限度内，施肥量和平均单产量之间的关系– B、产品产量与单位产品成本之间的关系– C、商品的流通费用与销售利润之间的关系– D、流通费用率与商品销售量之间的关系③变量之间的相关程度越低，则相关系数值（）A、越小B、越接近于0C、越接近于-1D、越接近于1④已知Σ(X-X¯)2是Σ(Y-Y¯)2的两倍，并已知Σ(X-X¯) (Y-Y¯)是Σ(Y-Y¯)2的1.2倍，则相关系数r为（）A、不能计算B、0.6C、1.2/D、多选题变量之间的不完全相关可以表现为（）A、零相关B、正相关C、负相关D、曲线相关E、相关系数为1求X与Y的相关系数二、一元线性回归1. 什么是回归分析？（内容）1)从一组样本数据出发，确定变量之间的数学关系式。
2)对这些关系式的可信程度进行各种统计检验，并从影响某一特定变量的诸多变量中找出哪些变量的影响显著，哪些不显著。
3)利用所求的关系式，根据一个或几个变量的取值来预测或控制另一个特定变量的取值，并给出这种预测或控制的精确程度。
回归分析与相关分析的区别1)相关分析中，变量 x 变量 y 处于平等的地位；回归分析中，变量 y 称为因变量，处在被解释的地位，x 称为自变量，用于预测因变量的变化。
2)相关分析中所涉及的变量 x 和 y 都是随机变量；回归分析中，因变量 y 是随机变量，自变量 x 可以是随机变量，也可以是非随机的确定变量。
3)相关分析主要是描述两个变量之间线性关系的密切程度；回归分析不仅可以揭示变量 x 对变量 y的影响大小，还可以由回归方程进行预测和控制。
多选题线性相关分析的特点表现为（）– A、两个变量之间的地位是对等关系– B、只能算出一个相关系数– C、相关系数有正负号– D、相关的两个变量必须都是随机变量– E、不反映任何自变量和因变量的关系回归模型的类型2. 一元线性回归1)涉及一个自变量的回归。
2)因变量y与自变量x之间为线性关系。
–被预测或被解释的变量称为因变量，用y表示。
–用来预测或用来解释因变量的一个或多个变量称为自变量，用x表示。
3)因变量与自变量之间的关系用一条线性方程来表示。
3. 一元线性回归模型（概念要点）1)当只涉及一个自变量时称为一元回归，若因变量y 与自变量 x 之间为线性关系时称为一元线性回归。
2)对于具有线性关系的两个变量，可以用一条线性方程来表示它们之间的关系。
3)描述因变量 y 如何依赖于自变量 x 和误差项ε的方程称为回归模型。
4）一元线性回归模型可表示为： y =（a+bx）+ ε◆y 是 x 的线性函数(部分)加上误差项。
◆线性部分反映了由于 x 的变化而引起的 y 的变化。
◆误差项ε是随机变量,反映了除 x 和 y 之间的线性关系之外的随机因素对y 的影响，不能由 x 和 y之间的线性关系所解释的变异性。
◆a和 b称为模型的参数。
5）基本假定◆误差项ε是一个期望值为0的随机变量，即E(ε)=0。
◆对于一个给定的 x 值，y 的期望值为E ( y ) = a+ b x。
◆对于所有的 x 值，ε的方差σ2都相同。
◆误差项ε是一个服从正态分布的随机变量，且相互独立，即ε~N( 0 ,σ2 )。
–独立性意味着对于一个特定的 x 值，它所对应的ε与其他 x 值所对应的ε不相关。
–对于一个特定的 x 值，它所对应的 y 值与其他 x所对应的 y 值也不相关。
4. 回归方程1)描述 y 的平均值或期望值如何依赖于 x 的方程称为回归方程。
2)一元线性回归方程的形式如下： E( y ) =β0+ β1x–方程的图示是一条直线，也称为直线回归方程。
–β0是回归直线在 y 轴上的截距，是当 x=0 时 y 的期望值。
–β1是直线的斜率，称为回归系数，表示当 x 每变动一个单位时，y 的平均变动值。
5. 估计（经验）回归方程1)总体回归参数β0和β1都是未知的，必须利用样本数据去估计。
2)用样本统计量a和b代替回归方程中的未知参数β0和β1，就得到了估计的回归方程。
3)简单线性回归中估计的回归方程为：yˆ = a + bx单选题劳动消耗和产量之间的回归方程为Y=18+2.1X，这意味着劳动消耗每增加一单位时，产量增加的单位为（）A、8B、2.1C、20.1D、2.1%6. 参数a和b的最小二乘估计一元回归方程数值试验1)使因变量的观察值与估计值之间的离差平方和达到最小来求得a和b的方法。
即：2)用最小二乘法拟合的直线来代表x与y之间的关系与实际数据的误差比其他任何直线都小。
3)根据最小二乘法的要求，可得求解a和b的标准方程如上图。
参数a和b的最小二乘估计（例题）某从事饮食业的企业家认为高校后勤社会化是一个很好的投资机会，他得到10组高校人数与周边饭店季营业额的数据资料，并想根据数据决策其投资规模。
7. 回归系数与相关系数的关系b-回归系数 r-相关系数单选题在线性相关的条件下，自变量的均方差为2，因变量均方差为5，而相关系数为0.8时，则其回归系数为（）A、8B、0.32C、2D、 12.5多选题①相关系数与回归系数（）- A、回归系数大于零则相关系数大于零- B、回归系数小于零则相关系数小于零- C、回归系数大于零则相关系数小于零- D、回归系数小于零则相关系数大于零- E、回归系数等于零则相关系数等于零②直线回归方程y=a+bx 中的b 称为回归系数,回归系数的作用是（）– A、可确定两变量之间因果的数量关系– B、可确定两变量的相关方向– C、可确定两变量相关的密切程度– D、可确定因变量的实际值与估计值的变异程度– E、可确定当自变量增加一个单位时,因变量的平均增加量三、线性回归方程拟合优度的测定1. 离差平方和的分解1)因变量 y 的取值是不同的，y 取值的这种波动称为变差。
变差来源于两个方面：-由于自变量 x 的取值不同造成的。
-除 x 以外的其他因素(如x对y的非线性影响、测量误差等)的影响。
2)对一个具体的观测值来说，变差的大小可以通过该实际观测值与其均值之差 y − y来表示。
图解三个平方和的关系三个平方和的意义1)总平方和(SST)总偏差-反映因变量的 n 个观察值与其均值的总离差。
2)回归平方和(SSR)回归偏差-反映自变量 x 的变化对因变量 y 取值变化的影响，或者说，是由于 x 与y 之间的线性关系引起的 y的取值变化，也称为可解释的平方和。
3)残差平方和(SSE)剩余偏差-反映除 x 以外的其他因素对 y 取值的影响，也称为不可解释的平方和或剩余平方和。
-2. 判定系数r21)回归平方和占总离差平方和的比例。
2)反映回归直线的拟合程度。
3)取值范围在 [ 0 , 1 ] 之间。
4)r2 →1，说明回归方程拟合的越好；r2→0，说明回归方程拟合的越差。
5)判定系数等于相关系数的平方，即r2＝(r)2。
r2等于多少？3. 估计标准误差 S yx1)实际观察值与回归估计值离差平方和的均方根。
2)反映实际观察值在回归直线周围的分散状况。
3)从另一个角度说明了回归直线的拟合程度。
4)计算公式为：S yx越小，拟合越好；S yx越大，拟合越差。
5）相关系数与估计标准误差在数量上具有以下关系：r值与估计标准误差负相关。
单选题①回归估计的估计标准误差的计量单位与（）– A、自变量相同– B、因变量相同– C、自变量及因变量相同– D、相关系数相同②计算估计标准误差的依据是（）– A、因变量的总变差– B、因变量的回归变差– C、因变量的剩余变差– D、因变量数列多选题估计标准误差是反映（）– A、回归方程代表性大小的指标– B、估计值与实际值平均误差程度的指标– C、自变量与因变量离差程度的指标– D、因变量估计值的可靠程度的指标– E、回归方程适用价值大小的指标判断题①回归系数b和相关系数r都可用来判断现象之间相关的密切程度。
