第5章线性系统频率特性测量和网络分析仪.

第五章 线性系统的频域分析频域分析法是应用频率特性研究线性系统的一种经典方法。

它以控制系统的频率特性作为数学模型，以伯德图或其他图表作为分析工具，来研究、分析控制系统的动态性能与稳态性能。

频域分析法由于使用方便，对问题的分析明确，便于掌握，因此和时域分析法一样，在自动控制系统的分析与综合中，获得了广泛的应用。

本章研究频率特性的基本概念、典型环节和控制系统的频率特性曲线、奈奎斯特稳定判据以及开环频域性能分析等内容。

§5-1 频率特性的基本概念一、频率特性的基本概念频率特性又称频率响应，它是系统（或元件）对不同频率正弦输入信号的响应特性，对于线性系统，若其输入信号为正弦量，则其稳态输出信号也将是同频率的正弦量，但其幅值和相位都不同与输入量。

下面以RC 电路为例，说明频率特性的基本概念。

图5-1所示的RC 电路，)(t u i 和)(0t u 分别为电路的输入电压和输出电压，电路的微分方程为：)()()(00t u t u dtt du Ti =+ 式中T=RC 为电路的时间常数。

RC 电路的传递函数为11)()(0+=Ts s U s U i （5-1） Rui )t图 5-1 RC 电路当输入电压为正弦函数t U t u i i ωsin )(=，则由式（5-1）可得22011)(11)(ωω+⋅+=+=s U Ts s U Ts s U i i 经拉氏反变换得电容两端的输出电压)sin(11)(122/220T tg t T U e T T U t u iT t i ωωωωω---+++=式中，第一项为输出电压的暂态分量，第二项为稳态分量，当∞→t 时，第一项趋于零，于是)sin(1|)(1220T tg t T U t u i t ωωω-∞→-+=)](sin[)(ωϕωω+=t A U i （5-2）式中：2211)(TA ωω+=，T tgωωϕ1)(--=，分别反映RC 网络在正弦信号作用下，输出稳态分量的幅值和相位的变化，二者皆是输入正弦信号频率ω的函数。

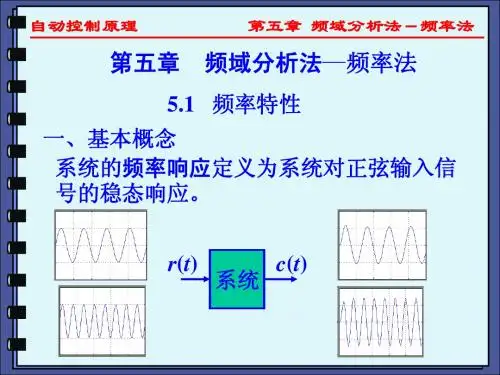
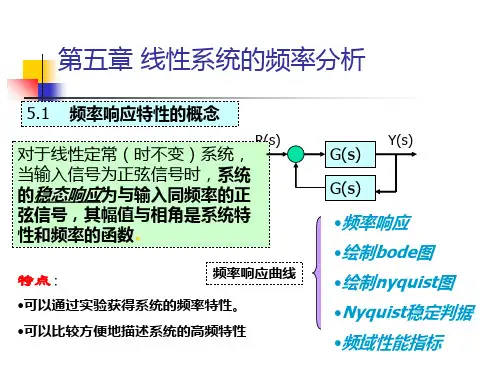
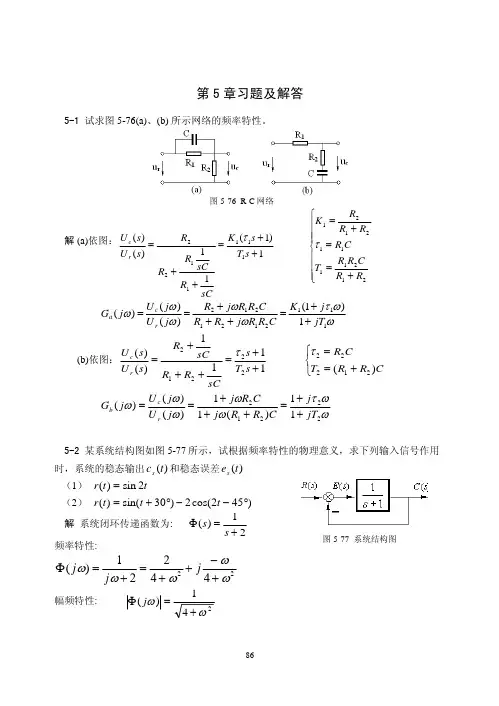
第5章习题及解答5-1 试求图5-76(a)、(b) 所示网络的频率特性。

图5-76 R-C 网络解 (a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(R R C R R T C R R R R K s T s K sCR sC R R R s U s U r c ττ ωωτωωωωω11121212121)1()()()(jT j K C R R j R R C R R j R j U j U j G r c a ++=+++==(b)依图：⎩⎨⎧+==++=+++=C R R T CR s T s sCR R sCR s U s U r c)(1111)()(2122222212ττ ωωτωωωωω2221211)(11)()()(jT j C R R j C R j j U j U j G r c b ++=+++==5-2 某系统结构图如图5-77所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出和稳态误差 )(t c s )(t e s图5-77 系统结构图（1）t t r 2sin )(= （2） )452cos(2)30sin()(°−−°+=t t t r 解 系统闭环传递函数为: 21)(+=Φs s 频率特性:2244221)(ωωωωω+−++=+=Φjj j幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωϕ= 系统误差传递函数: ,21)(11)(++=+=Φs s s G s e则 2arctan(arctan )(,41)(22ωωωϕωωω−=++=Φj j e e（1）当时, t t r 2sin )(=2=ω，r m =1则 ,35.081)(2==Φ=ωωj o 45)22arctan()2(−=−=j ϕo4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2()(o−=+Φ=t t j r t c m s ϕ)4.182sin(79.0)2sin()2()(o+=+Φ=t t j r t e e e m s ϕ （2） 当 )452cos(2)30sin()(°−−°+=t t t r 时:⎩⎨⎧====2,21,12211m m r r ωω o 5.26)21arctan()1(45.055)1(−=−===Φj j ϕ o 4.1831arctan()1(63.0510)1(====Φj j e e ϕ)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m s ϕϕ+−⋅Φ−++⋅Φ=oo)902cos(7.0)4.3sin(4.0oo−−+=t t )]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m s ϕϕ+−⋅Φ−++⋅Φ=oo )6.262cos(58.1)4.48sin(63.0oo−−+=t t 5-3 若系统单位阶跃响应h t e e t t t()..=−+≥−−11808049试求系统频率特性。

线性系统频率特性测量和网络分析由线性系统频域分析发展起来的频域测量技术在线性系统测量中具有特殊意义。

频域中有两个基本测量问题:信号的频谱分析、线性系统频率特性的测量。

如前所述，频谱分析仪可以完成对信号本身的分析以及非线性失真测量;对线性系统的频率特性测量和实现是本章将讲述的内容。

10.1线性系统频率特性测量频率响应是指线性网络对正弦输入信号的稳态响应，也称为频率特性。

网络的频率特性通常都是复函数，它的绝对值代表着频率特性中的幅度随频率变化的规律，称为幅频特性;相角或相位表征了网络的相移随频率变化的规律，称为相频特性。

线性网络的频率特性测量包括幅频特性测量和相频特性测量。

10.1.1幅频特性测量线性系统频率特性的基本测量方法取决于加到被测系统的测试信号。

经典方法是以正弦波点频测量为基础，这种静态的测量方法费时且不完整，常常会漏掉频率特性的突变信息或一些细节。

与之对应的是正弦波扫频测量，这是一种动态测量。

后来又发展到采用伪随机信号进行广谱快速测量，或者采用多频测量，即用具有素数关系的多个离散频率的正弦波集合作为测试信号的快速频率特性测量方法。

目前仍以正弦扫频测量为线性系统频率特性的经典测量方法。

1. 点频测量法为了测试各种无源器件，需要信号源对测量电路提供能源或激励信号。

测试要求信号源的频率必须能够在一定范围内调谐或选择。

早期的频率信号源主要靠机械方式实现频率调节，即通过改变振荡部分的谐振回路机械尺寸来调节。

这种机械式频率调谐信号源都是按照“点频”方式工作的，也就是每次只能将频率度盘放置到某一位置，输出某一所需的单一频率连续波信号。

对应的频率特性测量方法即为“点频测量”:测量元器件在一定频段内的特性曲线时，必须将信号源的频率依次设置调谐到各指定频点上，并分别测出各点上的参数之后，才能将各点数据连成完整的曲线。

点频测量方法很简单，但它存在明显的缺陷。

首先，点频测量所得的频率特性是静态的，无法反映信号的连续变化。

一种独特的仪器网络分析仪是一种功能强大的仪器, 正确使用时, 可以达到极高的精度。

它的应用也十分广泛, 在很多行业都不可或缺, 尤其在测量无线射频 (RF元件和设备的线性特性方面非常有用。

现代网络分析仪还可以应用于更具体的场合, 例如, 信号完整性和材料的测量。

随着业界第一款 PXI 网络分析仪— NI PXIe - 5630的推出, 你完全可以摆脱传统网络分析仪的高成本和大占地面积的束缚, 轻松地将网络分析仪应用于设计验证和产线测试。

网络分析仪的发展你可以使用图 1所示的 NI PXIe-5630矢量网络分析仪测量设备的幅度,相位和阻抗。

由于网络分析仪是一种封闭的激励 -响应系统, 你可以在测量 RF 特性时实现绝佳的精度。

当然, 充分理解网络分析仪的基本原理, 对于你最大限度的受益于网络分析仪非常重要。

在过去的十年中, 矢量网络分析仪由于其较低的成本和高效的制造技术, 流行度超过了标量网络分析仪。

虽然网络分析理论已经存在了数十年,但是直到 20世纪 80年代早期第一台现代独立台式分析仪才诞生。

在此之前, 网络分析仪身形庞大复杂,由众多仪器和外部器件组合而成,且功能受限。

NI PXIe-5630的推出标志着网络分析仪发展的又一个里程碑, 它将矢量网络分析功能成功地赋予了灵活,软件定义的 PXI 模块化仪器平台。

通常我们需要大量的测量实践, 才能实现精确的幅值和相位参数测量, 避免重大错误。

由于射频仪器测量的不确定性, 小的错误很可能会被忽略不计。

而网络分析仪作为一种精密的仪器能够测量出极小的错误。

网络分析理论网络是一个被高频率使用的术语,有很多种现代的定义。

就网络分析而言, 网络指一组内部相互关联的电子元器件。

网络分析仪的功能之一就是量化两个射频元件间的阻抗不匹配, 最大限度地提高功率效率和信号的完整性。

每当射频信号由一个元件进入另一个时, 总会有一部分信号被反射, 而另一部分被传输, 类似于图 2所示。