八年级数学每日一题共14题

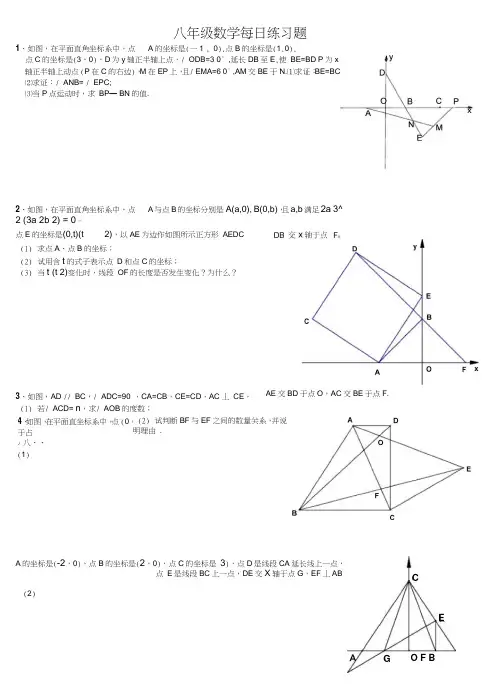
(2)八年级数学每日练习题1、如图，在平面直角坐标系中，点A 的坐标是(一1 , 0),点B 的坐标是(1,0),点C 的坐标是(3，0)，D 为y 轴正半轴上点，/ ODB=3 0° ,延长DB 至E ,使 BE=BD P 为x 轴正半轴上动点 (P 在C 的右边)，M 在EP 上，且/ EMA=6 0° ,AM 交BE 于N.⑴求证：BE=BC ⑵求证：/ ANB= / EPC;⑶当P 点运动时，求 BP — BN 的值.2、如图，在平面直角坐标系中，点 A 与点B 的坐标分别是 A(a,0), B(0,b)，且a,b 满足2a 3^2 (3a 2b 2) = 0。

点E 的坐标是(0,t)(t 2)，以AE 为边作如图所示正方形 AEDC(1) 求点A 、点B 的坐标；(2) 试用含t 的式子表示点 D 和点C 的坐标；(3) 当t (t 2)变化时，线段 OF 的长度是否发生变化？为什么？3、如图，AD // BC ，/ ADC=90°，CA=CB ，CE=CD ，AC 丄 CE ， (1) 若/ ACD= n ，求/ AOB 的度数；(2) 试判断BF 与EF 之间的数量关系，并说明理由 . A 的坐标是(-2，0)，点B 的坐标是(2，0)，点C 的坐标是 3)，点D 是线段CA 延长线上一点，点 E 是线段BC 上一点，DE 交X 轴于点G ，EF 丄AB 4、如图，在平面直坐标系中，点 (0， 于占J 八、、 (1)AE 交BD 于点O ，AC 交BE 于点F.CEGO F BF.若点G是DE的中点，试问线段BE和AD有何数量关系？为什么？在(1 )的条件下，求△ CGF的面积.y5、如图，在平面直角坐标系中，点A的坐标是(-t, 0)，点B的坐标是(t , 0)，点C的坐标是(0, t)，其中t>0 •点D 和点E分别是AC延长线和反向延长线上的点，CD=AE.CF丄BD 于点F，直线CF交X轴于点G,直线GE交DB于点M.(1)求证：GB平分/ CGM ;(2)试判断/ D与/ GEC之间的数量关系，并说明你的理由；1(3 )若AE= —AC，则点B是MD的中点吗？为什么？26、如图，点A、B在y轴正半轴上，/ DOB=60o，点C在OD上，且OC=OA , BC=BD，点C的纵坐标是1, AB=4.(1)求点A和点B的坐标；(2)求证：AC=DC.7、如图，点A和点B分别在X轴和y轴的正半轴上，AD平分/ BAO交y轴于点D, OC X AB于点C,交AD于点E,过点E作EF// AB，交OB于点F.(1) 求证：OE=OD ;(2) 若OE=2 , DF=1.8，求点B的坐标•8、如图，△ ABC是等边三角形，E是BC边上一动点(不与点B、C重合)，以CE 为一边在BC的另一侧作等边厶CED，连结BD , AE的延长线交BD于点F，连结FC.(1)求证：AE=BD ;(2)当点E在边BC上运动时(不与点B、C重合)，空一D匸的值是否发生变化？CF如果不变，求出其值；如果改变，清说明理由F9、(3) 若点P 为y 轴正半轴上一动点，以 AP 为直角边作等腰直角三角形 动时，OP —QR 的值是否发生变化？若不变，求出其值；若变化，请说明理由10、 (1) (1) (2) (2)如图2,连接 OP 、AB ，若/ BAO11、如图1,在平面角直角坐标系中，点 轴于点A 、点B. (1 )当直角/APB 绕点P 转动(保持与 值是否发生变化？说明你的理由； APQ ,/12、两块等腰直角三角形纸板按如图所示方式摆放，/ BACN ADE=9(0, AD AE 分别交BC 于点M N.(1) 请问以线段BM MN 和 CN 为边能否构成三角形？若能构成三角形，请判断三角形的形状；若不能构成三角形，请说明 理由• (2) 若将三角形纸板 ADE 绕点A 旋转至如图2所示位置，AE 交BC 延长线于点N,请问以线段BMMN 和CN 为边能否构成 三角形？为什么？13、在平面直角坐标系中，点 B 的坐标是(-3,3),过点B 作直线a 丄y 轴于点C ,作直线b 丄x 轴于点A ，点P 、Q 分别 是直线a 和直线b 上的点，/ POQ=45o.(1)如图1,点P 、Q 分别在线段BC 和线段AB 上，试求△ BPQ 的周长；图1 图2点Q 在线段AB 的延长线上，请问线段PQ 、BQ 和BP 之间有怎样的数量关系?为什么?(3) ________________________________ 如图3,点P 在线段BC 的反向延长线上，点 Q 在线段AB 的反向延长线上，请直接写出线段 数量关系： _____ •(2)如图2,点P 在线段BC 的延长线上, PQ 、BQ 和BP 之间的另一组对边相等、（6）12 个平行四边形的判定14、依据（1）一组对边平行、（2）一组对边相等、（3）一组对角相等、（4）另一组对边平行、（5）另一组对角相等、（7）一条对角线平分另一条对角线等条件可组成平行四边形的判定命题，请写出命题，并判断其真假，画图并写出证明或反例；16、已知P 是正方形 ABCD 边BC 上一点，PE! AP,且 PE=AP 连接(1)如图1求/ ECF 的度数；(2)如图2,连接AC,(3) 若正方形的边长为 4, CF=3,请直接写出BP 的长为17、P 是边长为4的正方形 ABCD 的边BC 上任一点，过 B 作BGL AP 于G,过C 作CEL AP 于E,连 (1)如图1,若P 是BC 的中点，求CE 的长；AG -CE(2)如图2,当P 在BC 边上运动时(不与 B C 重合)，求^AG —的值;BE(3)当 PB= 时，△ BCE 是等腰三角形。

八年级数学计算题每日基础练习1（1）. 先化简，再求值：（1+a ）（1﹣a ）+（a ﹣2）2，其中a=﹣3．、（2）. 因式分解2x 4﹣2 （3）．计算3 2-12（4）.解分式方程22311x x x（5）. 化简：222x x x 2x 1x x x 1x 2+-+÷++-+每日基础练习2（1）. 先化简，再求值：（x+y ）（x ﹣y ）﹣（4x 3y ﹣8xy 3）÷2xy，其中x=﹣1，．（2）.因式分解：3a 2﹣12ab+12b 2 （3）．化简212(1)211a a a a +÷+-+- （4）. 解方程：﹣1= （5）. 化简：（﹣）﹣﹣|﹣3|每日基础练习3（1）. 先化简，再求值：（x ﹣1）（x+1）﹣x （x ﹣3），其中x=3．（2）.因式分解：ax 2+2ax ﹣3a （3）．15)32125(⨯+（4）. 解分式方程：12422=-+-x xx ． （5）.（5）先化简，再求值：2211m 2mn nm n mn -+⎛⎫-÷ ⎪⎝⎭，其中m ＝－3，n ＝5．每日基础练习4（1）.化简： [(2x ＋y )2－(2x ＋y )(2x －y )]÷2y －21y（2）.因式分解：a ab ab 442+- （3）．(827－53)· 6（4）.解方程：． （5）. 化简求值： 221m 2m 11m 2m 4++⎛⎫-÷ ⎪+-⎝⎭，其中m ＝1。

每日基础练习5（1）. 先化简，再求值：[(5x ＋2y )(3x ＋2y )＋(x ＋2y )(x －2y )]÷4x ，其中x=2，y=－3．（2）.因式分解：()()a a a 322+-+ （3）．12)323242731(⋅--（4）.解方程：． （5）.化简求值：22312x x x 1x x 2x 1-⎛⎫-÷⎪+++⎝⎭，其中x=1．每日基础练习6（1）. 化简求值：(a 2＋3)(a －2)－a (a 2－2a －2)，其中a=122- （2）因式分解：x 2－4（x －1） （3）．化简：，（5）.解方程：23112x x x x -=-+-. （4）每日基础练习7（1）. 化简：(x ―1)2+(x +3)(x ―3)+(x ―3)(x ―1)； （2）.因式分解：22)3(4)2(--+m m（3）．先化简，再求值：，其中．（4）. 方程（5）.12(75＋313－48)每日基础练习81121231548333（1）. 22)1)2)(2(+-+-x x x x －（ （2）.因式分解：14-x ；（3）．先化简，再求值．，其中m=2．（4）. ）解方程：． （5）. )632)(632()232)(3(2-+-+每日基础练习9 班级 姓名（1）. 化简：[(x +y )2-y (2x +y )-8x ]÷2x ． （2）. 因式分解：a a a 81721623+-（3）．先化简，再求值：（1﹣）÷，其中a=﹣2．（4）. 13321++=+x x x x （5）. 2)153()347)(347(---+每日基础练习10（1）. 化简求值：()()()()[]x xy y y x y x y x 3442323÷--+-+-,其中2=x ,31=y .（2）. 因式分解： 432244y xy y x +- （3）．)62)(2332(-+（4）.解方程：311(1)(2)x x x x -=--+ （5）. 先化简，再求值：x 23x 1x 1x 1-⎛⎫÷+- ⎪--⎝⎭，其中x 3－2．每日基础练习11（1）.化简求值：.2)3)(3()2)(3(2-=-+-+-aaaxx其中，x=1（2）.因式分解： 9a2(x-y)+4b2(y-x)（3）．计算:1)21(248-+-（4）.解方程：32211xx x+=-+（5）. 化简求值：x35x2x2x2-⎛⎫÷+-⎪--⎝⎭，其中x3-每日基础练习12（1）. 解不等式：(x+3)(x-7)+8＞(x+5)(x-1). （2）.因式分解：aaa1812223-+-（3）．）先简化，再求值：x25x32x6x3--⎛⎫÷--⎪--⎝⎭，其中x2=-（4）.解方程：2227611x x x x x-=+--（5）.⎛÷⎝每日基础练习13（1）. 先化简，再求值：2(2)(21)(21)4(1)x x x x x+++--+，其中x=（2）.因式分解： 16－24(a－b)＋9(a－b)（3）．（4）.解方程：22510x x x x -=+-（5）. 先化简，再求值：÷（x+1﹣），其中x=﹣2每日基础练习14（1）. 22))(()32(y y x y x x --+-- （2）. 因式分解：22)23()32(y x y x --+（3）．先简化，再求值：21x 2x 11x x -⎛⎫-÷ ⎪⎝⎭＋，其中x 2=．（4）.解方程： 114112=---+x x x （5）. 26)1(30--+-π每日基础练习15（1）. 解方程(3x -2)(2x -3)=(6x +5)(x -1)+15． （2）. 因式分解：2442x y x y -（3）．先化简：，再求值，其中a=．（4）. 解方程：14143=-+--x x x （5）. 11181222-⎛⎫++ ⎪⎝⎭每日基础练习16（1）. 化简求值：x （x -1）+2x （x +1）－（3x -1）（2x -5）， （2）.171372222--+=--+x x x x x x 其中x =2．（3）．先化简，再求值：232224x x x x x x ⎛⎫-÷ ⎪-+-⎝⎭，其中x 取一个你喜欢的值求值（4）.分解因式：am 2﹣4an 2 （5）. )52)(103(-+ （6）.因式分解：4x 3﹣36x（7）. 22－ 3 －12 +( 3 +1) （8）. 22 －(3 －2)0+20（9）.)32)(532(+-（10）. )32)(532(+- （11）.(231⎛+ ⎝二次根式50道典型计算题1. 2484554+-+2. 2332326--3. 21418122-+- 4. 3)154276485(÷+-5.已知： 的值。

八年级上册每日一练习题一、选择题（每题3分，共30分）1. 下列关于二次根式的说法正确的是（）A. √9 = 3B. √9 = 3C. √9 = 3D. √9 = 32. 下列等式中，正确的是（）A. (a + b)² = a² + b²B. (a b)² = a² b²C. (a + b)² = a² + 2ab + b²D. (a b)² = a² 2ab + b²3. 下列关于平行四边形的性质，错误的是（）A. 对边平行且相等B. 对角相等C. 对角线互相平分D. 邻角互补4. 已知a = 3，b = 4，则a² + b²的值为（）A. 7B. 12C. 25D. 95. 下列关于圆的性质，正确的是（）A. 圆的半径等于直径的一半B. 圆的直径等于半径的两倍C. 圆的周长等于半径的两倍D. 圆的面积等于半径的平方6. 下列关于函数的说法，错误的是（）A. 函数是一种特殊的映射关系B. 函数的定义域是自变量的取值范围C. 函数的值域是因变量的取值范围D. 函数的图像是一条直线7. 下列关于概率的说法，正确的是（）A. 概率是描述事件发生可能性的数值B. 概率的取值范围是0到1C. 概率等于事件发生的次数除以总次数D. 概率等于事件不发生的次数除以总次数8. 下列关于二次函数的说法，错误的是（）A. 二次函数的图像是抛物线B. 二次函数的对称轴是x轴C. 二次函数的顶点坐标为（h，k）D. 二次函数的系数a决定了抛物线的开口方向9. 下列关于几何图形的变换，错误的是（）A. 平移变换不改变图形的形状和大小B. 旋转变换不改变图形的形状和大小C. 对称变换不改变图形的形状和大小D. 缩放变换改变图形的形状和大小10. 下列关于概率的公式，正确的是（）A. P(A∪B) = P(A) + P(B)B. P(A∪B) = P(A) P(B)C. P(A∪B) = P(A) + P(B) P(A∩B)D. P(A∪B) = P(A) P(B) + P(A∩B)二、填空题（每题3分，共30分）11. 若a² = 9，则a的值为______。

2016年11月11日姓名 分数1、同底数幂相乘公式：)(aa a n m =∙ 练习：①=∙54x x ②a a a a 643-∙=③=∙∙72x x x ④已知3=x a ，4=y a ，则y x a += 。

2、幂的乘方的公式：)()(a a n m = ；练习：①=53)5( ②=44)(y③5324)(a a a ∙+= ④已知：,2=m a则m a 3= 。

⑤已知：3,2==n m a a ，则n m a 23+= 。

3、积的乘方的公式：)()()(b a ab n = ；练习：①=-23)2(x ②=-332)2(c ab③4823)(b a ab ∙= ④=∙--b b a b a 54232)2( 。

⑤计算20142012)5.0(2-⨯的结果是 。

⑥计算4991000)41()2(⨯-的结果是（ ） A 、2 B 、4 C 、4- D 、41-4、同底数幂除法公式：)(aa a n m =÷，规定：=0a ，（其中a ）。

练习：①=÷91144 ，②=÷412b b ，③=-0)33( 。

④若1)2(0=-x ，则x 所满足的条件是（ ）。

A 、2>xB 、2<xC 、0≠xD 、2≠x⑤452a a a ÷∙= 。

⑥已知：12=x a ，4=y a ，则y x a-= 。

5、单项式乘法法则：例子：=∙∙⨯-=∙-52325232))()(52(52a y y x x a xy y x练习：①=-∙)3(2y x ②)4(32xc xy -∙-=③=-∙-)3()2(233ab a ④22)3()4(3xy x xy -+-∙-=6、单项式除法法则：例子：=÷÷÷-=÷-2243323243))()(412(412a y y x x y x a y x练习：①=÷-284)4(x x ②)4(1222xc c xy -÷-= 。

每日一题初中数学【每日一题】（第1期）1、如图，/ B0C=9，点A在0B上，且0A=1,按下列要求画图：以A为圆心，1为半径向右画弧交0C于点A,得第1条线段AA i;再以A i为圆心，1为半径向右画弧交0B于点A2, 得第2条线段A1A2；再以A为圆心，1为半径向右画弧交0C于点A,得第3条线段心… 这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则n= _______解析；由题意知；A0 - A^A^A = jfj4, - - t则ZAOA Y =20心厶］OA.= “卫具…’、:Z5OC = 9°.-.^^=18°, = 27% AA3A.B = 36= = 45°9 妝Y 90°解得n<10TH为整数，初中数学【每日一题】（第2期）2、已知：如图，△ ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB BC方向匀速移动，它们的速度都是1cm/s，当P到达点B时，P、Q两点停止运动.设点P的运动时间为t（s），当t为_____________________ 时，△ PBQ是直角三角答案：n=9形.* 匚答案：t=1秒或t=2秒解析：棍据题盍；“朮■叫硕AABC 中,AABO眈叫ZB=60° ,.'.BP= (3-t ) cm△PBQ 中* EPW-右6Q=tj若△PBQ是宜甬三角形」则ZBQR-50-1或ZBPQ=«〔1)当ZBOP^SO* 吋，理=¥»PPt = -(3-d；2解得：t=l(2)当ZBPQ-90* 吋丁BP = -BO解得：t=2二当日秒或"秒吋，APBQ是直角三角形初中数学【每日一题】(第3期)水滴石穿!3、如图，等腰△ ABC中，AB=AC / DBC=15 , AB的垂直平分线MN交AC于点D,则/ A 的度数是°.【解析】试题分析：设/ A=x°,根据MN为中垂线可得：/ ABD=/ A=x°,则/ ABC=(x+15) °，根据AB=AC可得：/ C=Z ABC=(x+15) °，则根据厶ABC的内角和定理可得：x+x+15+x+15=180 °，解得：x=50 ° .初中数学【每日一题】(第4期)锲而不舍，金石可镂！如图，在△ ABC中，/ ABC与/ ACB的平分线相交于点0,过点0作DE// BC,分别交AB AC于点D E,若AB=6, AC=5则厶ADE的周长是答案：50°答案：11【解析】试题分析：根据题意可得：△ BDO^A COE是等腰三角形，OD=BD OE=EC则厶ADE的周长=AD+DE+AE=AD+DO+OE+AE=AD+BD+AE+CE=AB+AC=6+5=11.考点：（1）、角平分线的性质；（2）、等腰三角形的性质•初中数学【每日一题】（第5期）小水长流，贝U能穿石！如图所示，三角形ABC的面积为1 . AP垂直/ B的平分线BP于点P.则三角形PBC的面积是____________________ .【解析】试题分析：过点P作PEL BP,垂足为P,交BC于点E,由角平分线的定义可知/ ABP=/ EBP 结合BP=BP以及/ APB=/ EPB=90 即可证出厶ABP^A EBP（ASA，进而可得出AP=EP根据三角形的面积即可得出，再根据— art1故答案为：-考点：等腰三角形的判定与性质；角平分线的定义；三角形的面积；全等三角形的判定与性质.初中数学【每日一题】（第6期）立志不坚，终不济事！如图，△ ABC是等腰直角三角形，延长BC至E使BE=BA过点B作BD1AE于点(1)求证：BF=2AD(2)若CE龙，求AC的长试题解析：(1)证明：•「△ ABC是等腰直角三角形,••• AC=BC/ FCB" ECA=90 ,••• ACL BE, BD L AE,•••/ CBF+Z CFB=90，/ DAF+Z AFD=90 ,vZ CFB Z AFD•••/ CBF Z CAEAC^BC^CBF=ZCAE在厶BCF与△ ACE中, ，•••△ BCF^A ACE••• AE=BFv BE=BA BD L AE,••• AD=ED 即AE=2AD••• BF=2AD(2)由(1)知厶BCF^A ACE••• CF=CE血,•••在Rt△ CEF中, EF=JH+E=2,v BD L AE, AD=ED•AF=FE=2•AC=AF+CF=2+ .考点：全等三角形的判定与性质；勾股定理初中数学【每日一题】（第7期）已知，如图，△ ABC是等边三角形，AE=CD BQLAD 于Q, BE 交AD 于点P ,初中数学【每日一题】（第8期）如图，/ MON=90 , △ ABC 的顶点 A B 分别在OM ON 上，当A 点从0点出发沿着 0M 向 右运动时，同时点 B 在ON 上运动，连结 0C.若AC=4, BC=3 AB=5贝U 0C 的长度的最大【解析】30度角的直角三角形.考点：全等三角形的判定与性质；等边三角形的性质；含试题分析：取AB中点E,连接OE CE在直角三角形AOB中，OE= AB,利用勾股定理的逆定理可得△ ACB是直角三角形，所以CE= AB,利用OE+C匡OC所以OC的最大值为OE+CE即OC的最大值=AB=5考点：勾股定理的逆定理初中数学【每日一题】（第9期）精诚所至，金石为开！著名画家达芬奇不仅画艺超群，同时还是一个数学家、发明家•他曾经设计过一种圆规如图所示，有两个互相垂直的滑槽（滑槽宽度忽略不计），一根没有弹性的木棒的两端A、B 能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆来•若AB=20cm则画出的圆的半径为_______________________ cm试题解析：连接OP•••△ AOB是直角三角形，P为斜边AB的中点,丄••• OP^ AB■/ AB=20cmOP=i0cm考点：直角三角形斜边上的中线.初中数学【每日一题】（第10期）最可怕的是比你优秀的人还比你努力！如图，在△ ABC中，AB=AC点E为BC边上一动点（不与点B、C重合），过点E 作射线EF交AC于点F,使/ AEF=/ B.£C-(1)判断/ BAE与/ CEF的大小关系，并说明理由；(2)请你探索：当△ AEF为直角三角形时，求/ AEF与/ BAE的数量关系.【解析】(1)/ BAE/ FEC理由如下：•••/ B+/ BAE/ AEC / AEF=/ B，•••/ BAE/ FEC(2)如图1,当/AFE=90 时，•••/ B+/ BAE/ AEF/ CEF/ B=/ AEF=/ C,•••/ BAE/ CEF•••/ C+/ CEF=90，•••/ BAE/ AEF=90，即/ AEF与/ BAE的数量关系是互余；如图2，当/ EAF=90时，•••/ B+/ BAE/ AEF/ 1，/ B=/ AEF=/ C,•••/ BAE/ 1，vZ C+Z 1+Z AEF=90 ,••• 2Z AEF+Z 1=90°,即2Z AEF与Z BAE的数量关系是互余.A【点评】此题考查了等腰三角形的性质以及外角的性质，此题难度适中，注意掌握分类讨论思想的应用.初中数学【每日一题】（第11期）耐心是一切聪明才智的基础！如图，△ ABC的三边AB BC CA长分别是20、30、40,其三条角平分线将△ ABC分成三个三角形，则*心：*曲：鼻「削）等于试题分析：由角平分线的性质可得，点O到三角形三边的距离相等，即三个三角形的AB BC CA的高相等，禾I」用面积公式即可求解.过点O作ODL AC于D, OELAB于E，OF L BC于F，v O是三角形三条角平分线的交点，二OD=OE=OF v AB=20 BC=30 AC=4Q .•声^： $皿：'s =2: 3: 4. 故答案为：2：3：4.考点：角平分线的性质；三角形的面积.初中数学【每日一题】（第12期）如图，已知/ AOB=60，点P在0A上，OP=8点M N在边0B上，PM=PN若MN=2 贝U 0M=________________ .解：过P作PCL MN•/ PM=PN••• C为MN中点.WC = SC = = I°■在Rt△ OPC中，/ AOB=60，•••/ OPC=30，• 2OC=OP=，OC=4初中数学【每日一题】（第13期）能坚持别人不能坚持的,才能拥有别人不能拥有的如图，Rt△ ABC中，/ ACB=90 , CD是斜边AB上的高，角平分线AE交CD于H, EF丄AB于F,下列结论：①/ ACD M B;②CH=CE=EF③AC=AF④ CH=HD其中正确的结论为（）A.①②④B.①②③C.②③D.①③•••/ B和/ ACD都是/ CAB的余角，•••/ ACD M B,故①正确;v CDL AB, EF丄AB••• EF// CD，•••/ AEF=/ CHE•••/ CEH/ CHE••• CH=CE=EF故②正确；v角平分线AE交CD于H,•••/ CAE/ BAE•••△ ACE^A AFE（AAS ,••• AC=AF故③正确；CH=CE=E^HD故④错误.故：正确答案选B初中数学【每日一题】（第14期）如图，在△ ABC中, AC=BC / C=90 , D是AB的中点，DEI DF,点E, F 分别如图，连接CDv BC=AC / BCA=90•••△ ABC是等腰直角三角形v D为AB中点• BD=CD=AD CD平分/ BCA CDL AB•••/ A+Z ACD=/ ACD+Z FCD=90•••/ A=Z FCDvZ CDF Z CDE=90 Z CDE Z ADE=90•Z ADE玄CDF在厶ADE和厶CFD中vZ A=Z FCD AD=CD Z ADE Z CDF•△ADE^A CFD( ASA初中数学【每日一题】（第15期）耐心和恒心总会得到报酬的。

初二（下）A 组每日一题（2018年5月7日——2018年5月13日）编辑老师：邢克辉.1．（5.7星期一）化简求值：(23-x x －2+x x )·x x 42- ，其中x = －4.2．（5.8星期二）25. （本题5分）在数学课上，老师对同学们说：“你们任意说出一个a 的值（a ≠－1，0），我就立刻知道式子12a )111(2++÷+-a a a 的计算结果”。

请你说出其中的道理。

3.（5.9星期三）20.一个容器装有1升水，按照如下方法把水倒出：第1次倒出升水，第2次倒出水量是升的，第3次倒出水量是升的，第4次倒出水量是升的，……，第n 次倒出水量是升的，按照这种倒水的方法， n 次一共倒出的水量为升。

4.（5.10星期四） 如果,那么的值为5. （5.11星期五）每年3月12日是植树节，某学校植树小组若干人植树，植树若干棵。

若每人植4棵，则余20棵没人植，若每人植8棵，则有一人比其他人植的少(但有树植)，问这个植树小组有多少人？共有多少棵树？21213131414151n 111+n 31=-x x 221xx +6.（5.12星期六）某电脑经销商计划购进一批电脑机箱和液晶显示器，若购电脑机箱10台和液液晶显示器8台，共需要资金7000元；若购进电脑机箱2台和液示器5台，共需要资金4120元．（1）每台电脑机箱、液晶显示器的进价各是多少元？（2）该经销商购进这两种商品共50台，而可用于购买这两种商品的资金不超过22240元．根据市场行情，销售电脑机箱、液晶显示器一台分别可获利10元和160元．该经销商希望销售完这两种商品，所获利润不少于4100元．试问：该经销商有哪几种进货方案？哪种方案获利最大？最大利润是多少？7.（5.13星期日）如下数表是由从1开始的连续自然数组成，观察规律并完成各题的解答．12 3 45 6 7 8 910 11 12 13 14 15 1617 18 19 20 21 22 23 24 2526 27 28 29 30 31 32 33 34 35 36…………………………………………………（1）表中第8行的最后一个数是_________，第8行共有__________个数；（2）用含n的代数式表示：第n行的第一个数是__________，最后一个数是__________，第n行共有___________个数；（3）写出第803行各数之和______________________________。

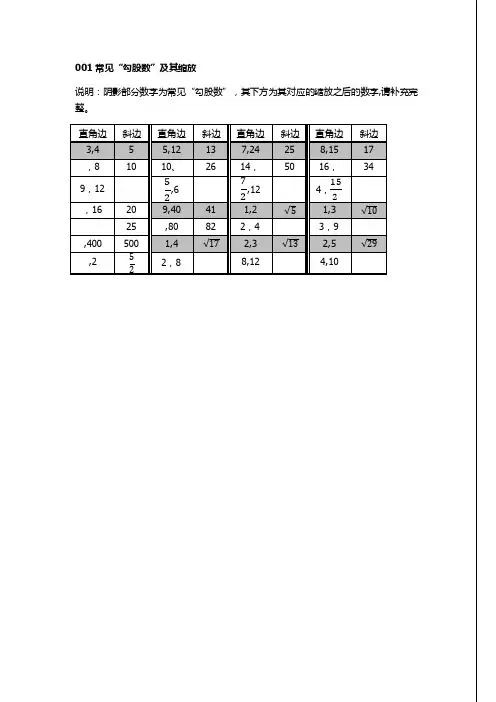
001常见“勾股数”及其缩放说明：阴影部分数字为常见“勾股数”，其下方为其对应的缩放之后的数字,请补充完整。

002特殊三角形的三边关系1、含30°+60°的直角三角形 如图，则BC:AC:AB=1 ,即AB=2BC ，BC=AB AC= BC ，BC=练习（1） 若BC=6，则AC= ，AB= ；若BC= ，则AC= ，AB=____ （2） 若AB=5，则BC= ,AC= ；若AB= ，则BC= ,AC=____ （3） 若AC=4 ，则BC= ，AB= ；若AC=6，则BC= ，AB=_____2、含45°的直角三角形 如图，则BC:AC:AB=1 , 即BC=AC AB= BC ，BC=练习（4） 若BC=6，则AB= ；若BC= ，则AB=_____ （5） 若AB=6，则BC= ,；若AB= ，则BC=_____ （6） 若AC=4 ，则AB= ；若AC= ，则AB=_____3、含120°的等腰三角形如图，则BC:AC:AB=1:1: , 即BC=AC AB= BC ，BC=练习（7） 若BC=6，则AB= ；若BC= ，则AB=_____ （8） 若AB=6，则BC= ,；若AB= ，则BC=_____4、等边三角形的面积等边三角形的边长为a ，则其面积为_________ 120°的等腰三角形腰长为a ，则其面积为______AA003特殊平行四边形的性质请在具有这个性质的图形下面画“√”004特殊平行四边形的判定正方形005“对称+点点最值”菱形ABCD的边长为2，∠ABC=60°，E是AD边的中点，点P是对角线BD上的动点，求AP+PE的最小值。

006对称+点线最值如图，菱形ABCD中，AB=6，∠ABC=45°，点P为对角线BD上一点，M 为BC上一点，则PC+PM的最小值为007对称+点点差最大值如图，在正方形ABCD中，AB=8，AC与BD交于点O，N是OA的中点，点M在BC边上，且BM=6，P为对角线BD上一点，则PM-PN的最大值为008转化+点线最值已知三角形ABC 中，∠ACB=90°，AC=6，BC=8，点D 是AB 上一个动点，DE ⊥AC ，DF ⊥BC 。

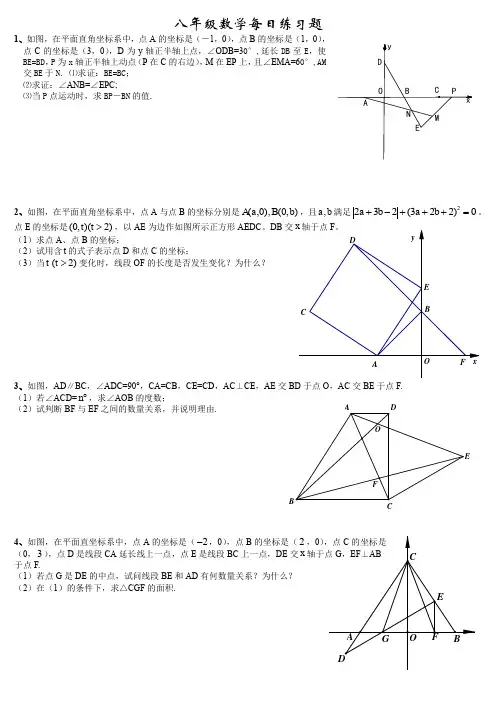
C八年级数学每日练习题1、如图，在平面直角坐标系中，点A 的坐标是（－1，0），点B 的坐标是（1，0），点C 的坐标是（3，0），D 为y 轴正半轴上点，∠ODB=30°,延长DB 至E ，使BE=BD ，P 为x 轴正半轴上动点（P 在C 的右边），M 在EP 上，且∠EMA=60°,AM 交BE 于N. ⑴求证：BE=BC ； ⑵求证：∠ANB=∠EPC;⑶当P 点运动时，求BP －BN 的值.2、如图，在平面直角坐标系中，点A 与点B 的坐标分别是),0(),0,(b B a A ，且b a ,满足2232(322)0a b a b +-+++=。

点E 的坐标是(0,)(2)t t >，以AE 为边作如图所示正方形AEDC 。

DB 交（1）求点A 、点B 的坐标； （2）试用含t 的式子表示点D 和点C 的坐标；（3）当t (2)t >变化时，线段OF 的长度是否发生变化？为什么？3、如图，AD ∥BC ，∠ADC=90°，CA=CB ，CE=CD ，AC ⊥CE ，AE 交BD 于点O ，AC 交BE 于点F. （1）若∠ACD=n ︒，求∠AOB 的度数；（2）试判断BF 与EF 之间的数量关系，并说明理由.4、如图，在平面直坐标系中，点A 的坐标是（2-，0），点B 的坐标是（2，0（0，3），点D 是线段CA 延长线上一点，点E 是线段BC 上一点，DE 交x 于点F.（1）若点G 是DE 的中点，试问线段BE 和AD 有何数量关系？为什么？ （2）在（1）的条件下，求△CGF 的面积.5、如图，在平面直角坐标系中，点A的坐标是（t-，0），点B的坐标是（t，0），点C的坐标是（0，t），其中0t>.点D 和点E分别是AC延长线和反向延长线上的点，CD=AE.CF⊥BD 于点F ,直线CF交x轴于点G，直线GE交DB于点M.（1）求证：GB平分∠CGM；（2）试判断∠D与∠GEC之间的数量关系，并说明你的理由；（3）若AE=12AC，则点B是MD的中点吗？为什么？6、如图，点A、B在y轴正半轴上，∠DOB=60º，点C在OD上，且OC=OA，BC=BD，点C的纵坐标是1，AB=4.（1）求点A和点B的坐标；（2）求证：AC=DC.7、如图，点A和点B分别在x轴和y轴的正半轴上，AD平分∠BAO交y轴于点D，OC⊥AB于点C，交AD于点E，过点E作EF∥AB，交OB于点F.（1）求证：OE=OD；（2）若OE=2，DF=1.8，求点B的坐标.8、如图，△ABC是等边三角形，E是BC边上一动点（不与点B、C重合），以CE 为一边在BC的另一侧作等边△CED，连结BD，AE的延长线交BD于点F，连结FC. （1）求证：AE=BD；（2）当点E在边BC上运动时（不与点B、C重合），EF DFCF+的值是否发生变化？如果不变，求出其值；如果改变，清说明理由.yx O M E D C BA9、如图，在平面角直角坐标系中，点A （0，2）、点B （-4,0），OD=3OA ，点B 与点C 关于y 轴对称，DE ⊥AB 于点E ，DM=AB.（1）求点M 的坐标； （2）求证：△AMC 是等腰直角三角形.10、如图，在平面角直角坐标系中，A （–2，0），B （0，3），C （3，0），D （0，2）.（1）求证：AB=CD 且AB ⊥CD ；（2）以A 为直角顶点在第二象限内作等腰直角三角形ABE ，过点E 作EF ⊥x 轴于点F ，求点F 的坐标；（3）若点P 为y 轴正半轴上一动点，以AP 为直角边作等腰直角三角形APQ ，∠P 运动时，OP -QR 的值是否发生变化？若不变，求出其值；若变化，请说明理由.11、 如图1，在平面角直角坐标系中，点P 的坐标是（3，3），以点P 为顶点的直角∠APB 分别交y 轴正半轴和x 轴正半轴于点A 、点B.（1）当直角∠APB 绕点P 转动（保持与y 轴正半轴和x 轴正半轴相交）时，OA+OB 的值是否发生变化？说明你的理由；（2）如图2，连接OP 、AB ，若∠BAO 的平分线交OP 于点C ，CD ⊥AO 于点D ，求CD +2AB的值.12、两块等腰直角三角形纸板按如图所示方式摆放，∠BAC=∠ADE=90º，AD 、AE 分别交BC 于点M 、N.（1）请问以线段BM 、MN 和CN 为边能否构成三角形？若能构成三角形，请判断三角形的形状；若不能构成三角形，请说明理由.（2）若将三角形纸板ADE 绕点A 旋转至如图2所示位置，AE 交BC 延长线于点N ，请问以线段BM 、MN 和CN 为边能否构成三角形？为什么？图1 图213、在平面直角坐标系中，点B 的坐标是（33， ），过点B 作直线a ⊥y 轴于点C ，作直线b ⊥x 轴于点A ，点P 、Q 分别是直线a 和直线b 上的点，∠POQ=45º.（1）如图1，点P 、Q 分别在线段BC 和线段AB 上，试求△BPQ 的周长；图 1 图 2（2）如图2，点P 在线段BC 的延长线上，点Q 在线段AB 的延长线上，请问线段PQ 、BQ 和BP 之间有怎样的数量关系？为什么？（3）如图3，点P 在线段BC 的反向延长线上，点Q 在线段AB 的反向延长线上，请直接写出线段PQ 、BQ 和BP 之间的数量关系：.图 314、依据（1）一组对边平行、（2）一组对边相等、（3）一组对角相等、（4）另一组对边平行、（5）另一组对边相等、（6）另一组对角相等、（7）一条对角线平分另一条对角线等条件可组成平行四边形的判定命题，请写出12个平行四边形的判定命题，并判断其真假，画图并写出证明或反例；图1A(P)图2P FE D C B A15、点P 在正方形ABCD 的边AD 所在的直线上，以BP 为对角线作正方形BEPF ，连结CE 。

1．a，b，c是三角形的三边长，化简|a﹣b﹣c|﹣|b﹣c+a|+|c﹣a﹣b|后等于（）A．b+a﹣3c B．b+c﹣a C．3a+3b+3c D．a+b﹣c2．如图，把△ABC沿EF翻折，叠合后的图形如图，若∠A＝60°，∠1＝95°，则∠2的度数是（）A．15°B．20°C．25°D．35°3．如果一个多边形的内角和是外角和的5倍，那么这个多边形的边数是．4．如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E．（1）若∠B＝35°，∠E＝25°，求∠CAE的度数；（2）证明：∠BAC＝∠B+2∠E．1．如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C＝122°，则∠1+∠2的度数为（）A．116°B．100°C．128°D．120°2．如图，△ABC中，∠B＝40°，∠C＝30°，点D为边BC上一点，将△ADC沿直线AD折叠后，点C落到点E处，若∠BAE＝50°，则∠DAC的度数为°．3．如图，在△ABC中，AD是BC边上的高，AE是∠BAC的平分线，若∠B＝70°，∠C ＝40°，则∠DAE的度数为．4．如图，直线AB⊥CD于点G，交EF于点H，射线GM交EF于点M，已知∠AGM：∠DGM＝2：7，∠AHF比∠DGM大10°，求∠GHM的度数．1．如图，CE是△ABC的外角∠ACD的平分线，若∠B＝30°，∠ACE＝60°，则∠A＝（）A．60°B．100°C．90°D．80°2．若一个多边形的一个内角为144°，则这个图形为正（）边形．A．十一B．十C．九D．八3．如图，大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α，再沿直线前进8米，到达点C后，又向左旋转α角度，照这样走下去，第一次回到出发地点时，他共走了72米，则每次旋转的角度α为（）A．30°B．40°C．45°D．60°4．如图，点D，E，F分别是三角形ABC的边BC，AB，AC上的点，EF∥BC，∠1＝∠2，∠EDG＝90°．（1）判断线段DE与AB的位置关系，并说明理由．（2）若∠2＝60°，求∠FED的度数．1．如图，线段AB、CD相交于点O，连接AD、CB，∠DAB和∠BCD的平分线AP和CP 相交于点P，则∠P与∠D、∠B之间存在的数量关系为（）A．∠P＝2（∠B﹣∠D）B．C．D．2．如图，在四边形ABCD中，∠C＝110°，与∠BAD，∠ABC相邻的外角都是120°，则∠α的值为（）A．50°B．55°C．60°D．65°3．如图，BD＝BC，点E在BC上，且BE＝AC，DE＝AB．（1）求证：△ABC≌△EDB；（2）判断AC和BD的位置关系，并说明理由．1．如图，直线a∥直线b，Rt△ABC的直角顶点A落在直线a上，点B落在直线b上，若∠1＝18°，∠2＝32°，则∠ABC的大小为．2．若对图1中星形截去一个角，如图2，再对图2中的角A，B，E，F如法进一步截去，如图3，则图中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N＝度．3．.如图，点C、D在线段AB上，且AC＝BD，AE＝BF，AE∥BF，连接CE、DE、CF，求证CF＝DE．1．小聪利用最近学习的数学知识，给同伴出了这样一道题：假如从点A出发，沿直线走6米后向左转θ，接着沿直线前进6米后，再向左转θ……如此下去，当他第一次回到A 点时，发现自己走了72米，θ的度数为（）A．30°B．36°C．60°D．72°2．若一个正多边形的一个外角为72°，则这个正多边形的内角和为（）A．360°B．540°C．720°D．900°3．如图，AB＝BD，要使△ABC≌△DBC，还需要补充一条件：（填一个即可）．4．如图所示，已知CD＝BD，点E、F分别是CD、BD的中点，∠CAF＝∠BAE，∠B＝∠C．求证：AE＝AF．1．如图（），BE是△ABC的高．A．B．C．D．2．如图，∠B＝30°，∠CAD＝65°且AD平分∠CAE，则∠ACD等于（）A．95°B．65°C．50°D．80°3．如图，在Rt△ABC的斜边AB上截取AD＝AC，过点D作DE⊥AB交BC于E，则有（）A．DE＝DB B．DE＝CE C．CE＝BE D．CE＝BD4．如图，在四边形ABCD中，E是对角线AC上一点，连接DE，AD∥BC，AC＝AD，∠CED+∠B＝180°．△ADE与△CAB全等吗？为什么？八年级上册数学每日一练81．如图，在△ABC中，AB＝AC，点D是BC边的中点，连接AD，点P在AD上，连接BP，CP，过点D作DE⊥BP，DF⊥CP，垂足分别为EF，则下列结论：①BD＝CD；②△BDE≌△CDF；③DE＝PE；④△BCP是等腰三角形．其中正确的有．（填序号）2．如图所示，△ABC≌△AEF．在下列结论中，不正确的是（）A．∠EAB＝∠F AC B．BC＝EFC．CA平分∠BCF D．∠BAC＝∠CAF3．如图，正方形ABCD和正方形AEFG有公共点A，点B在在线段DG上．判断DG与BE的位置关系，并说明理由．八年级上册数学每日一练91．在△ABC中，D，E分别是AC、BC上的点，过点D作DF⊥AB，DG⊥BC，垂足分别是点F，G，连接DE，若DF＝DG，BE＝DE，则下面三个结论：①BF＝BG；②DE∥BF；③△ADF≌△CDG．其中正确的是（）A．①③B．②③C．①②D．①②③2．如图，在正方形OABC中，O是坐标原点，点A的坐标为（1，），则点C的坐标是（）A．（﹣，1）B．（﹣1，）C．（﹣，1）D．（﹣，﹣1）3．如图，在△AOB和△COD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝50°，（1）试说明：AC＝BD；（2）AC与BD相交于点P，求∠APB的度数．八年级上册数学每日一练101．如右图，AO、BO、CO分别平分∠BAC、∠ABC、∠ACB，OD⊥BC，△ABC的周长为12，OD＝2，则△ABC的面积为．2．如图，△ABC的三边AB、BC、CA长分别是30、40、50，∠ABC和∠ACB的角平分线交于O，则S△ABO：S△BCO：S△CAO等于（）A．1：1：1B．1：2：3C．2：3：4D．3：4：53．如图1，∠DAB＝90°，CD⊥AD于点D，点E是线段AD上的一点，若DE＝AB，DC ＝AE．（1）判断CE与BE的关系是．（2）如图2，若点E在线段DA的延长线上，过点D在AD的另一侧作CD⊥AD，并保持CD＝AE，DE＝AB，连接CB，CE，BE，试说明（1）中结论是否成立，并说明理由．1．在如图所示的3×3网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数是（）A．4个B．3个C．2个D．1个2．如图，△ABC中，∠ABC的角平分线与∠ACB的角平分线交于点P，若点P到边BC的距离为1，△ABC的周长为12，则△ABC的面积为（）A．6B．7C．8D．93．如图，在△ABC和△DEF中，AB＝DE，∠B＝∠DEF，请你再补充一个条件，能直接运用“SAS”判定△ABC≌△DEF，则这个条件是（）A．∠ACB＝∠DEF B．BE＝CF C．AC＝DF D．∠A＝∠F4．如图，在△ABC中，D，E是BC边上的两点，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAE＝60°，则∠BAC的度数为．5．如图，在△ABC中，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E．若DE＝1，AC ＝4，则△ADC的面积为．6．如图，已知∠1＝∠2，AC＝AE，不添加任何辅助线，再添加一个合适的条件：，使△ABC≌△ADE．（只写出一种即可）1．如图，E是△ABC的边AC的中点，过点C作CF∥AB，过点E作直线DF交AB于D，交CF于F，若AB＝9，CF＝6.5，则BD的长为．2．如图，在△ABC中，∠ACB＝90°，点D为AC边上一点，ED⊥AC，CE⊥AB，AB＝CE，若BC＝2，DE＝5，则线段AD的长为．3．如图，在△ABC中，∠ABC＝45°，过点C作CD⊥AB于点D，过点B作BM⊥AC于点M，连接MD，过点D作DN⊥MD，交BM于点N，CD与BM交于点E．下列结论：①∠ABM＝∠ACD；②DM＝DN；③∠AMD＝45°；④S△DNE＝S△ADM.其中正确结论有．（填写序号即可）4．如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠P+∠Q＝度．5．如图，△ABC≌△ADE，∠B＝90°，∠C＝26°，∠DAC＝14°，则∠EAC＝．6．如图，AD是△ABC的角平分线，DF⊥AB于点F，点E，G分别是边AB，AC上的点，且DE＝DG，则∠AED+∠AGD＝度．1．如图，CA⊥AB于点A，AB＝4，AC＝2，射线BM⊥AB于点B，一动点D从点A出发以2个单位/秒的速度沿射线AB运动，E为射线BM上一动点，随着点D的运动而运动，且始终保持ED＝BC，若点D运动t秒（t＞0），△EDB与△BCA全等，则t的值为．2．如图，在正方形方格中，各正方形的顶点叫做格点，三个顶点都在格点上的三角形称为格点三角形．图中△ABC是格点三角形，请你找出方格中所有与△ABC全等，且以A为顶点的格点三角形．这样的三角形共有个（△ABC除外）．3．如图，在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝8，CD＝4，则四边形ABCD的面积是．4．如图，已知AE⊥AB，AF⊥AC．AE＝AB，AF＝AC，BF与CE相交于点M．求证：（1）EC＝BF；（2）EC⊥BF；（3）连接AM，求证：AM平分∠EMF．。