机械设计基础弹簧
- 格式:ppt
- 大小:1.01 MB
- 文档页数:21






机械设计基础机械设计中的弹簧应用与设计机械设计基础:机械设计中的弹簧应用与设计弹簧是机械设计中常见的零件,它通过自身弹性变形储存和释放能量,起到连接、减震、传动等作用。
在机械系统中,合理地应用和设计弹簧,可以提高系统的性能和可靠性。
本文将从弹簧的基本原理、常见类型和设计要点等方面进行探讨。
1. 弹簧的基本原理弹簧是一种能够储存和释放机械能的元件,具有弹性形变的特性。
当外力作用在弹簧上时,弹簧将发生形变,并产生恢复力,使其返回初始状态。
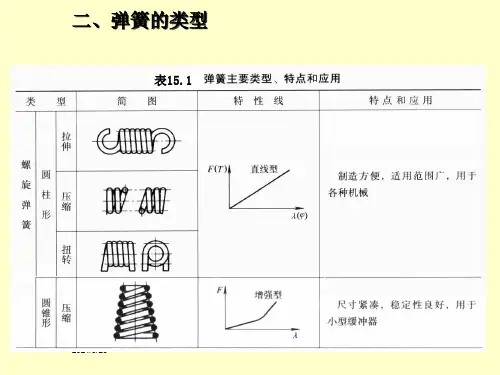
根据力的作用方向和弹簧的形态,弹簧可分为拉伸弹簧、压缩弹簧和扭转弹簧三种类型。
2. 弹簧的常见类型2.1 拉伸弹簧拉伸弹簧是最常见的弹簧类型,广泛应用于各类机械系统。
它通常以线圈状或螺旋状的形式存在,如拉力试验机中的测力弹簧、扩展门中的拉簧等。
在设计拉伸弹簧时,需要考虑合理的拉伸长度、线径、材料选择等因素,以确保其满足给定的工作要求。
2.2 压缩弹簧压缩弹簧是指在内部受到外部压力时产生形变的弹簧。
它通常具有柱状或圆柱状的形态,如汽车避震器中的压缩弹簧、各类压缩机中的缓冲弹簧等。
在设计压缩弹簧时,需要考虑合理的压缩长度、线径、材料选择等因素,以确保其在不同工作环境下能够保持合适的弹性变形。
2.3 扭转弹簧扭转弹簧,也被称为扭簧,是指通过对弹簧材料施加扭转力矩并产生旋转变形的弹簧。
它通常以圆柱形或线圈形的形态存在,如手摇发电机中的发电机弹簧、汽车转向系统中的扭力弹簧等。
在设计扭转弹簧时,需要考虑合理的扭转角度、线径、材料选择等因素,以确保其在扭转过程中有足够的弹性变形能力。
3. 弹簧的设计要点弹簧的设计在机械系统中扮演着重要角色,合理的设计能够提高系统的性能和可靠性。
以下是一些常见的设计要点:3.1 弹簧刚度弹簧刚度是指单位长度或单位角度下的力学特性,通过刚度的选择可以调节弹簧的变形量和恢复力。
在设计中需要根据系统的要求,选取合适的弹簧刚度,以确保系统在正常工作范围内保持稳定性。




机械设计基础弹性系数的公式
机械设计基础弹簧的刚度,(即弹性系数,中学物理叫倔强系数k);
F:弹簧所受的载荷;
λ:弹簧在受载荷F时所产生的变形量;
G:弹簧材料的切变模量;(钢为8×104MPa,青铜为4×
104MPa)
d:弹簧丝直径;
D2:弹簧直径;
n:弹簧有效圈数;
C:弹簧的旋绕比(又称为弹簧指数)
由上式可知。
当其它条件相同时,C值愈小的弹簧,刚度愈大,亦即弹簧愈硬;反之则愈软。
还应注意到,C值愈小,弹簧内、外侧的应力差愈悬殊,卷制愈难,材料利用率也就愈低,并且在工作时将引起较大的扭应力。
所以在设计弹簧时,一般规定C≥4,且当弹簧丝直径d越小时,C值越宜取大值。
其实上面这个公式是根据微段弹簧丝ds受转矩后扭转dθ,从而产生微量变形dλ,再将dλ积分而得到圆弹簧丝螺旋弹簧在受载荷F所产生的变形量。
第16章 弹簧一、基本内容及要求本章的重点是圆柱形螺旋拉伸、压缩弹簧的应力和变形的计算,结构尺寸的确定和材料的选择等。
二、自学指导1.圆柱形螺旋拉伸、压缩弹簧的应力。
一个受轴向力F 作用的圆柱形螺旋压缩弹簧,用通过弹簧轴线的平面把弹簧分割成两部分并取上面部分作为研究对象。
弹簧丝截面处剪力F 与扭矩T ,分别为与弹簧上面部分相平衡的内力系。
剪力F 在截面内引起剪应力τ',如图16.1,a 所示,可以认为剪应力在截面上是均匀分布的。
扭矩T 作用在弹簧丝截面上引起的扭剪应力τ'',如图16.1,b 所示。
剪应力τ'和扭剪应力τ''迭加,可得弹簧丝截面上最大应力τ,如图16.1,c 所示。
不难看出,在弹簧丝内侧的A '点上,τ'与τ''方向是一致的,所以该处应力最大,即τ=τ'+τ''2.圆柱形螺旋拉伸、压缩弹簧的变形同圆柱形螺旋拉伸、压缩弹簧的应力公式推导前的假设一样,对圆截面弹簧丝卷成的圆柱形螺旋拉伸、压缩弹簧变形的计算,也认为弹簧的螺旋升角α很小,故可认为:用通过弹簧轴线的平面,切下的弹簧丝截面,仍为圆形截面。
从公式τ=τ'+τ''=⎪⎪⎭⎫ ⎝⎛+232218D d d FD π中可以看出,括号内第二项比第一项小得多,所以通常可以略去,而只考虑弹簧由扭矩22D F T =所产生的扭转。
图16.2表示通过弹簧轴线两相邻平面bO 1、bO 2,将弹簧切下长为ds 的一个微段。
由于ds 很小,可以近似地认为在变形前弹簧截面中心的半径bO 1和bO 2与弹簧丝轴线O 1O 2是在同一个水平面上,并构成一扇形O 1bO 2。
对微段ds 来说,O 1和O 2两截面上的扭矩⎪⎭⎫ ⎝⎛=22D F T 即 图16.1图16.2为作用于两端截面上的外力偶矩,这样就引起了截面O 2相对于截面O 1转了一个φd 角,PGJ Tds d =φ(式中G 为弹簧材料的剪切弹性模量;J P 为极惯矩)。