信息率失真函数
- 格式:ppt
- 大小:627.50 KB
- 文档页数:37




信息率失真函数的定
义
所谓信息率失真,是指在数据传输过程中造成的原本可以正常识别的信息被破坏而无法被正确识别的现象。
它通常由某种外部的影响,如噪声、干扰或错误编码等因素造成。
具体来说,信息率失真函数是一种度量从输入到输出信号中信息率“差异”的函数。
它定义为信号输出中比原始信号(输入)中丢失的信息的分数。
可以用以下公式来表示信息率失真:
I_R=1-D_R
其中,I_R是信息率失真,D_R是失真率,它定义为输出信号(受失真影响的信号)比输入信号(未受失真影响信号)失真的部分所占的比例,单位是%。
![[信息与通信]第10讲 信息率失真函数](https://uimg.taocdn.com/d018b36c3069a45177232f60ddccda38376be1de.webp)


信息率失真函数r(d)
信息率失真函数是信息论中对信源的提取率和失真之间关系的描述函数,用于量化信息传输过程中的信源失真。
信息传输中存在两个基本要素,即提取率和失真。
提取率指的是通过传输信道提取出的有效信息的比例,
而失真则是指提取出的信息与原始信息之间的差异。
信息率失真函数通常被用来评估压缩编码的性能。
在压缩编码中,为
了减小数据的传输量,我们会对数据进行压缩,并通过编码算法将其表示
为较短的二进制代码。
压缩过程中的失真表示为编码后恢复的数据与原始
数据之间的差异。
在设计压缩编码算法时,我们希望能够在提取率和失真之间达到一个
平衡。
提取率越高,我们能够从信道中提取出更多的有效信息;而失真越小,恢复的信息与原始信息的差距越小。
信息率失真函数可以帮助我们在
这两个方面之间进行权衡。
在信息论中,常用的信息率失真函数有均方误差函数和最大误差概率
函数。
均方误差函数衡量的是编码恢复的数据与原始数据之间的平方差的
期望,可以通过最小化均方误差来实现较低的失真。
而最大误差概率函数
则衡量的是编码恢复的数据与原始数据之间的最大差异的概率,可以通过
最小化最大误差概率来实现较低的失真。
总结来说,信息率失真函数是信息论中用于量化信源提取率和失真之
间关系的函数。
它可以帮助我们在设计压缩编码算法时找到提取率和失真
之间的平衡点,以达到较高的提取率和较低的失真。
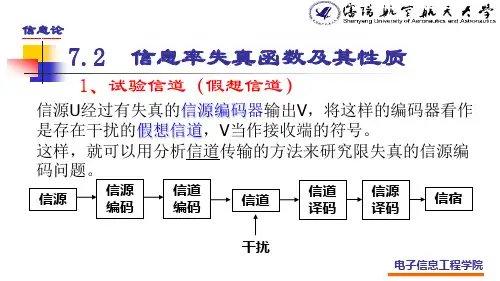



信息率失真函数的物理意义
信息率失真函数(Information Rate-Distortion Function)是在一定失真度量下,对于给定的信源,最低要求的信息传输速率。
它描述了信源与信宿之间信息传输的效率,是信源编码理论中的基本概念之一。
信息率失真函数的物理意义可以从以下几个方面解释:
1. 失真度量:信息率失真函数是基于一定的失真度量来定义的。
失真度量是指对于信源中的不同符号或信号,它们在解码后与原始信号之间的差异程度。
失真度量的种类很多,常见的有对称失真度量和非对称失真度量。
2. 信息传输速率:信息率失真函数描述了在一定的失真限制下,最低要求的信息传输速率。
这个速率是在信源编码中追求的目标,因为较低的信息传输速率通常可以降低编码成本和传输成本,同时提高信息传输的效率。
3. 信源编码定理:信息率失真函数是信源编码定理中的基本概念之一。
信源编码定理指出了对于任意给定的信源,存在一种最优的编码方式,使得编码后的信息传输速率达到信息率失真函数所描述的值。
因此,信息率失真函数为信源编码提供了理论基础和指导。
4. 信息率失真函数的优化:信息率失真函数的优化是指在给定失真限制下,寻找最低的信息传输速率。
这个过程通常涉及到编码算法和码本设计等方面,是信源编码理论中的重要研
究方向之一。
通过优化信息率失真函数,可以提高信息传输的效率和可靠性,降低编码和传输成本。
总之,信息率失真函数是描述信源与信宿之间信息传输效率的基本概念,它在信源编码理论中具有重要的作用和意义。