当前位置：文档之家 › 第10讲 信息率失真函数的计算

第10讲 信息率失真函数的计算

  • 格式：pdf
  • 大小：241.04 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

平均失真和信息率失真函数

平均失真和信息率失真函数

解：失真矩阵为
d 10
1 0
00..55
说明: (1) 最常用的失真函数
均方失真函数： 绝对失真函数： 相对失真函数：
d(xi,yj)=(xi-yj)2 d(xi,yj)= d(xi,yj)=
误码失真函数： d(xj,yj)=
xi y j xi y j / xi
如果xj≠yj，就产生了失真。失真的 大小，用一个量来表示，即失真
函数d(xi,yi),以衡量用yj代替xi所引 起的失真程度。
一般失真函数定义为
d
(
xi
,
y
j
)

0, a,
a0
xi y j xi y j
如何定义失真矩阵? 将所有的失真函数 d(xi,yj)，i=1,2,…,n；j＝1,2,…,m排
离散矢量信源符号失真函数定义为： 如果假定离散矢量信源符号为矢量序列X＝
{传符x1输号x2…后序x，列i…y接jx=收n[}y，端j1y其j收2…中到yNj矢N长]则量符失序号真列序函Y列=数{yx1定iy=2[…义xi1yx为ji…2…yxmi}N，]，其经中信N道长
式接d中收Nd端(x(收ikx,到yijk第,)是yj个信jN源)长输符出号N1第yji中个k的NN1长第d符k个(号x符xii中k号,的yjyk的第jk失k个)真符函号数x。ik，
p（x）＝{0.5，0.5}，
信道矩阵分别为:p'ij 00..2600..84,
p' 'ij


0.9 0.2
求: 互信息。
00..81
解：因为p(xiyj)＝p(xi)p(yj/xi)； 用p’ij代人得 p’（x1y1）=0.3，p’（x1y2）＝0.2， p’（x2y1）=0.1，p’（x2y2）＝0.4

信息率失真函数

信息率失真函数
平均失真 ：
描述某个信源在某一试验信道传输下的 失真大小,它对信源和信道进行了统计平 均,是从总体上描述整个系统的失真
8
3、L长序列编码平均失真
❖ 如X编长l…果 码 符假 后 号Xn,定 序}输,其离 列出中散y符j=L信[号长y源j1序符y输j2列号…入Y序y=符j列L{Y]号x1iY序=2[…列xi1YXxil＝2……{YXxmi1L}X],,其经2…中信L源
❖ 离散无记忆信源
13
例2 已知编码器输入的概率分布为p(x)={0.5 ,0.5} 信道矩阵 求互信息
14
若编码器输入的概率分布不变仍为p(x)={0.5 ,0.5} 但信道矩阵 求互信息
• 可见当p(x)一定时,I (X,Y)随信道矩阵p(yj|xi)而变。 • 因为p(x)分布一定时,信道受干扰不同所能传递的
信道容量：
信息率失真函数：
16
信道容量和信息率失真函数的区别
2、反映的事物不同
• 信道容量：
– 假定信道固定的前提下,选择一种试验信源使信息 传输率最大。
– 它所反映的是信道传输信息的能力,是信道可靠传 送的最大信息传输率。
• 一旦找到了信道容量,它就与信源不再有关,而是信
道特性的参量,随信道特性的变化而变化
6
4.11、.2单平符号均离失散信真源的平均失真
❖ x是i和随y机j都变是量随,有机限变失量真,所时以的失信真源函（数总d(体xi,）yj)失也 真值只能用数学期望表示
❖ 将失真函数的数学期望称为平均失真：
7
2、两者的区别平均失真
失真函数d(xi,yj)： 描述了某个信源符号通过传输后失真的 大小
信息量是不同的。 • 当p(x)一定时,I (X,Y)是关于p(yj|xi)的下凸函数。 • 因此当改变p(yj|xi)时,I (X,Y)有一极小值。

信息率失真函数及其性质

信息率失真函数及其性质
电子信息工程学院
信息论
7.2
信息率失真函数及其性质
D允许试验信道 若p(ui)和d(ui，vj)已定，则可将在满足失真限度条件下的与 某种转移概率分布pij相对应的某种信源编码方法看成一个假 想信道，而所有可能的编码方法就构成了一个信道的集合BD
2、信息率失真函数
B D p(vj / ui ) : D D
电子信息工程学院
信息论
7.2
信息率失真函数及其性质
3、信息率失真函数的性质
3.1 R(D)的定义域 (0, Dmax ) (1) Dmin和R(Dmin) 因为D是非负函数d(u，v)的数学期望，因此D是非负的，其下 界为0，即： Dmin ＝0 。此时，对应于无失真的情况，相当于 无噪声信道，所以信道的信息率等于信源的熵，即
电子信息工程学院
信息论
7.2
信息率失真函数及其性质
2、信息率失真函数
将此问题对应到信道，即为接收端V需要获得的有关U的信 息量，也就是互信息I(U；V)。这样，选择信源编码方法的 问题就变成了选择假想信道的问题，符号转移概率p(vj/ui)就 对应信道转移概率。 平均失真由信源分布 p(ui)、假想信道的转移概率 p(vj/ui) 和失真函数 d(vj，ui) 共同决定。
p(v j / ui） p(v j )
再次强调，在研究R(D)时，我们引用的条件概率p(v|u) 并没有实际信道的含义，只是为了求平均互信息的最小 值而引用的、假想的可变试验信道。
电子信息工程学院
信息论
7.2
信息率失真函数及其性质
2、信息率失真函数
实际上这些假想的信道所对应的仅仅是各种不同的有失真 的信源编码方法，或信源压缩方法。 所以，改变试验信道求最小值，实质上是选择某一种编码 方式使信息传输率为最小，也就是在保真度准则下，使信 源的压缩率最高。 信息率失真函数R(D)是信源在限定最大失真D条件下信源输 出的信息率的下界，是理论上的最佳值（最小值）。

信息率失真函数的定

信息率失真函数的定

信息率失真函数的定
义
所谓信息率失真，是指在数据传输过程中造成的原本可以正常识别的信息被破坏而无法被正确识别的现象。

它通常由某种外部的影响，如噪声、干扰或错误编码等因素造成。

具体来说，信息率失真函数是一种度量从输入到输出信号中信息率“差异”的函数。

它定义为信号输出中比原始信号（输入）中丢失的信息的分数。

可以用以下公式来表示信息率失真：
I_R=1-D_R
其中，I_R是信息率失真，D_R是失真率，它定义为输出信号（受失真影响的信号）比输入信号（未受失真影响信号）失真的部分所占的比例，单位是%。

[信息与通信]第10讲 信息率失真函数

[信息与通信]第10讲 信息率失真函数

1 log 2e 2
2
D
1 2
R(D) log 2D
N
X
Y
反向加性高斯实验信道
1 2 D
2 2 D
R(D) 1 log 2
2D
R(D) 0
R(D)
2
D
2 D
S(D)
高斯信源的率失真函数
C
R(D)
I (X ;Y ) 的上凸函数 I (X ;Y ) 的下凸函数
I (X ;Y ) 的极大值
p(b 2
/
a) 1
(1
p)(1
e2S
)
p(b 1
/
a 2
)
(1 p) peS p(1 e2S )
p(b2
/
a2
)
(1 p) peS (1 p)(1 e2S
)
n
D(S)
m i p(ai ) p(bj )d (ai , bj )eSd (ai ,b j )
i1 j1
e S
1 eS
n
R(S) SD(S) p(ai ) ln i i 1
0
...
a
... ... ... ...
a
a
...
a
a 1
汉明失真
0 1 1
1
0
1
1
1
0
2 d(ai ,bj ) (bj ai )2 平方误差失真函数
平均失真度
失真函数d(ai，bj)是随机变量，失真函数的数 学期望称为平均失真度，记为
nm
D E[d(ai ,bj )]
作业：4.1 4.3 4.10 4.11
4.1 信息率失真函数
4.1.1 失真函数和平均失真度

计算信息率失真函数曲线

计算信息率失真函数曲线

计算信息率失真函数曲线信息率失真函数是指在给定平均失真度量下最小化信源数据率的函数。

它可以用来表示编码方案的效率。

下面是一个简单的例子，展示如何计算信息率失真函数曲线。

假设我们有一个二元信源，产生两个符号0和1，它们的出现概率分别为0.4和0.6。

我们希望将这个信源编码成另一个二元序列，用尽量小的码长来表示。

例如，我们可以用一个3位码来表示每个符号，例如0表示为000，1表示为001。

在这种情况下，我们得到的平均码长为2.4位，因为0的概率是0.4，需要3位码，1的概率是0.6，也需要3位码，所以平均码长是(0.4*3+0.6*3)=2.4位。

但是我们发现，这种编码方案并不是最优的，因为它使用了相同的码长来表示两个不同的符号，而0的概率更小，可以使用较短的码来表示。

因此，我们需要找到一种更好的编码方案，使得平均码长更小。

为了找到最优的编码方案，我们可以考虑信息率失真函数，它定义了信源数据率和失真之间的关系。

对于离散的信源，信息率失真函数定义为：R(D) = min{H(X): D(X,Y) <= D}其中，H(X)是信源的熵，D(X,Y)是表示信源X和编码后的序列Y之间的平均失真度量，D是允许的最大失真度量。

在我们的例子中，信源的熵为H(X)=-0.4*log2(0.4)-0.6*log2(0.6)=0.97095。

我们可以使用汉明码来表示这个信源，因为它是一种具有最小平均码长的编码方案。

汉明码基于两个符号之间的汉明距离，即它们不同的位数。

对于我们的信源，我们可以使用一个长度为2的汉明码。

具体来说，我们将0表示为00，将1表示为11，这样编码后的序列长度为2，平均码长为2*0.4=0.8位。

为了计算信息率失真函数曲线，我们需要计算不同的允许失真度量对应的最小信源数据率。

例如，当允许的最大失真为0.01位时，最小的信源数据率是0.8位，即汉明码的平均码长。

对于其他失真度量，我们可以使用类似的方法计算相应的信源数据率。

信道率失真函数

• 无论是无噪信道还是有噪信道: R＜C – 总能找到一种编码使在信道上能以任意小的错 误概率,以任意接近C的传输率来传送信息 R＞C – 就必须对信源压缩,使其压缩后信息传输率R小 于信道容量C,但同时要保证压缩所引入的失真 不超过预先规定的限度。
• 信息压缩问题就是对于给定的信源,在满足平均 失真 D D 的前提下,使信息率尽可能小。
10
失真函数
失真函数形式可以根据需要任意选取,最常 用的有:
• 均方失真: d(xi , y j ) (xi y j )2
适于
连续
• 绝对失真: d (xi , y j ) | xi y j |
信适源于
离散
• 相对失真: d (xi , y j ) | xi y j | / | xi |
5
4.1 平均失真和 信息率失真函数
6
• 在实际问题中，信号有一定的失真是可 以容忍的。但是当失真大于某一限度后， 信息质量将被严重损伤，甚至丧失其实 用价值。
• 要规定失真限度，必须先有一个定量的 失真测度。
• 为此引入失真函数。
7
4.1.1 失真函数
• 假如某一信源X,输出样值xi , xi∈{a1,a2,…an},经 信道传输后变成yj , yj ∈{b1, b2,…bm},如果:
4
• 人们的视觉和听觉都允许有一定的失真，电影 和电视就是利用了人的视觉残留，使人没有发 觉影片是由一张张画面快速连接起来的。耳朵 的频率响应也是有限的，在某些实际场合中只 需保留信息的主要特征就够了。所以，一般可 以对信源输出的信息进行失真处理，降低信息 率，提高传输率。那么在允许一定程度的失真 条件下，能够把信源信息压缩到什么程度，至 少需要多少比特的信息率才能描述信源呢？本 章主要讨论在一定程度的失真情况下所需的最 少信息率，从分析失真函数、平均失真出发， 求出信息率的失真函数。

信道率失真函数

• 平均失真：
– 描述某个信源在某一试验信道传输下的失真 大小,它对信源和信道进行了统计平均,是从总 体上描述整个系统的失真。
16
L长序列编码情况的平均失真
• 如果假定离散信源输出符号序列X＝{X1X2… Xl… XL},其中L长符号序列xi =[xi1xi2…xiL],经信源编码后, 输出符号序列Y={Y1Y2…Yl…YL},其中L长符号序列
失真函数
失真函数形式可以根据需要任意选取,最常 用的有:
• 均方失真: d(xi , y j ) (xi y j )2
适于
连续
• 绝对失真: d (xi , y j ) | xi y j |
信适源于
离散
• 相对失真: d (xi , y j ) | xi y j | / | xi |
信源
• 误码失真:
22
信息率失真函数R(D)
• 由于互信息取决于信源分布和信道转移概率分 布，根据2.2节所述，当p(xi)一定时,互信息I是 关于p(yj|xi) 的U型函数,存在极小值。因而在上 述允许信道PD中可以寻找一种信道pij，使给定 的信源p(xi)经过此信道传输后，互信息I(X;Y) 达到最小。该最小的互信息就称为信息率失真 函数R(D)，即
yj=[yj1yj2…yjL ],则失真函数定义为
dL (xi ,
yj)
1 L
L l 1
d (xil
,
y jl
)
• 平均失真
1 L
1L
DL L l1 E[d ( xil , y jl )] L l1 Dl
式中Dl是第l个符号的平均失真。
17
4.1.3 信息率失真函数R(D)
• 如图所示，信源X经过有失真的信源编码器输出Y，将 这样的编码器看作存在干扰的假想信道，Y当作接收端 的符号。这样就可用分析信道传输的方法来研究限失真 信源问题。

第10章 率失真函数

N ˆ j) P( x ˆ j / x k )] P ( x i ) 注意到 [ P( x k )PD ( x ˆ j / x i ) PD ( x ˆ j / x i ) k 1 PD ( x
N ˆ l ) log P( x ˆ l )] [ P( x ˆ j / x i ) l1 PD ( x N ˆ j) PD ( x ˆ l ) log P( x ˆ l )] [ P( x ˆ j ) l1 ˆ j / xi ) PD ( x PD ( x
i 1 j1
N
N
D限制下的条件极值
第10章 率失真函数
ˆ) 令 {I(X; X ˆ j / xi ) PD ( x ˆ l / x k )d ( x k , x ˆ l ) D] k [ PD ( x ˆ l / x k ) 1]} S[ P( x k )PD ( x
DD
第10章 率失真函数
4、测试信道 满足保真度准则的所有数据处理信道 离散信源的测试信道
ˆ / X ) {P ( X ˆ / X ) : D D} PD ( X
ˆ 1 / x1 ) PD ( x ˆ1 / x2) PD ( x P (x ˆ ˆ D 2 / x1 ) PD ( x 2 / x 2 ) ˆ PD (X / X) ... ... ˆ N / x1 ) PD ( x ˆ N / x2) PD ( x ˆ1 / xN) ... PD ( x ˆ 2 / xN) ... PD ( x ... ... ˆ N / x N ) ... PD ( x
p (1 p)2S S ˆ1 / x2 ) PD ( x 2 2S (1 p)(1 2 ) (1 p) p2S ˆ 2 / x2) PD ( x (1 p)(1 2 2S )

信息率失真函数及信源编码定理的应用

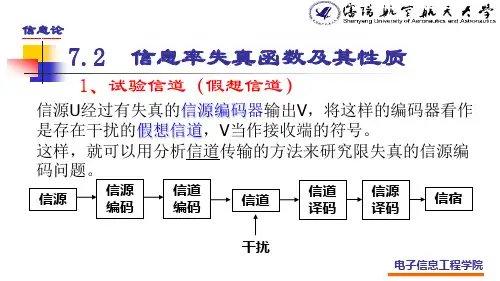
《信息论与编码》课程自学报告题目：信息论与编码自学报告学号：姓名：任课教师：联系方式：二零一四年2 月15 日1 自学内容阐述1.1 信息率失真函数1.1.1 失真函数与平均失真度失真函数：设离散信源概率分布为： 经信道传输后输出序列为: ，对任一 指定一个非负数 称为单个符号的失真度（或称失真函数）。

失真函数用来表征信源发出一个符号i a ，而在接收端再现成符号j b 所引起的误差或失真。

d 越小表示失真越小，等于0表示没有失真。

可以将所有的失真函数排列成矩阵的形式： 平均失真度：由于i a 和j b 都是随机变量，所以失真函数),(j i b a d 也是随机变量，限失真时的失真值，只能用它的数学期望或统计平均值，因此将失真函数的数学期望称为平均失真度，记为1.1.2 信息率失真函数的定义由于互信息取决于信源分布和信道转移概率分布，当信源的分布概率已知时，互信息I 是关于p(bj/ai) 的下凸函数，存在极小值。

该最小的互信息就称为信息率失真函数R(D)： 对于离散无记忆信源，R(D)可以写成：);(m in )()()/(N N P p N Y X I D R N D i j ∈=αβ1.1.3 信息率失真函数的性质 率失真函数的定义域： 。

允许失真度D 的下限可以是零，即不允许任何失真的情况。

率失真函数对允许平均失真度的下凸性：设21,D D 为任意两个平均失真，10≤≤a ，则有： )(,),(,),(),( , , , , ,)( 2121⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡n i n i a p a p a p a p a a a a X P X }...{21m b b b Y =),(j i b a 0),(≥ji b a d ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=),(...),(),(............),(...),(),(),(...),(),(][212221212111m n n n m m b a d b a d b a d b a d b a d b a d b a d b a d b a d D ∑∑∑∑====-===n i mj j i i j i n i m j j i j i ji b a d a b p a p b a d b a p b a d E D 1111),()/()(),()()],([);(min )()/(Y X I D R D i j P a b p ∈=min max 0D D D ≤≤≤1212((1))()(1)()R aD a D aR D a R D +-≤+-率失真函数的单调递减和连续性：由信息率失真函数的下凸性可知， R(D)在),(max min D D 上连续。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。