18.2(2)正比例函数的图像

1、正比例函数
定义：
形如y=kx（k为常数,且k≠0），我们就说y是x的正比例函数。

正比例函数是特殊的一次函数【一次函数的一般形式为y=kx+b（b不为0，k为常数）】。

图象作法:
a.列表(待定系数)
b.描点
c.连线
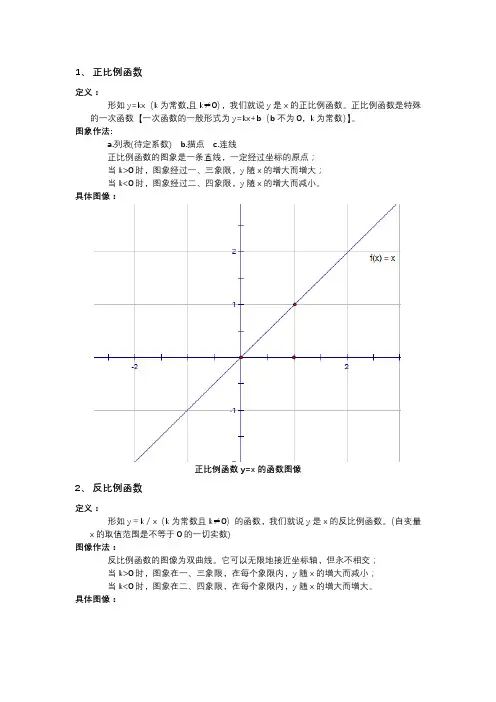
正比例函数的图象是一条直线，一定经过坐标的原点；
当k>0时，图象经过一、三象限，y随x的增大而增大；
当k<0时，图象经过二、四象限，y随x的增大而减小。

具体图像：
正比例函数y=x的函数图像
2、反比例函数
定义：
形如y＝k／x（k为常数且k≠0）的函数，我们就说y是x的反比例函数。

（自变量x的取值范围是不等于0的一切实数)
图像作法：
反比例函数的图像为双曲线。

它可以无限地接近坐标轴，但永不相交；
当k>0时，图象在一、三象限，在每个象限内，y随x的增大而减小；
当k<0时，图象在二、四象限，在每个象限内，y随x的增大而增大。

具体图像：
反比例函数y=1/x的函数图像。

18.2(2)正比例函数的图像一、课前练习已知y是x的正比例函数,且当x=4时,y=8.求y与x之间的函数解析式.二、阅读理解1.阅读教材P60～62.2.一般地,正比例函数y=kx (k是常数,k≠0)的图像是经过和的一条 .我们把正比例函数y=kx的图像叫做 .3.用描点法画函数图像的一般步骤:(1) ;(2) ;(3) .4.阅读中遇到的问题有三、新课探索如何画正比例函数y=2x的图像?它的图像是什么?直角坐标平面内任意一点都有唯一确定的坐标(x,y); 反过来,以任意给定的一对有序实数(x,y)为坐标,都可以在直角坐标平面内唯一确定一个点.想一想:由以上所述,你会画正比例函数y=2x的图像了吗?例题1 在直角坐标平面内画正比例函数y=2x的图像.操作画函数y=-2x的图像.(1)列表:(2)描点:(3)连线:观察函数y=2x与函数y=-2x的图像,看看它们有哪些相同的特点.例题2 在同一直角坐标平面内,分别画出下列函数的图像: y=3x, y=x, y=31x.四、课内练习1.正比例函数y=kx 的图像是___________,它一定经过点______和 _____.2.函数y=kx(k ≠0)的图像经过点(-21,5),写出函数解析式.这个函数图像经过哪几个象限?你是怎么判断的?3.在同一直角坐标平面内画出两个函数图像: (1)y=4x 与y=41x; (2)y=-31x 与y=-3x.18.2（2）正比例函数一、填空题1．若函数y =(a-2)x +b+3是正比例函数，且过点（－1，3），则a= ,b= .2．已知正比例函数图象上一点到x 轴距离与到y 轴距离之比为1︰2，则此函数解析式是 .3．若函数y=5x,当-2≤X ≤1时，y 的取值范围是_____________________ 二、选择题1．．函数y =3 x 的图象一定不经过点………………………………………（ ） A 、（1， 3） B 、（－1，－3） C 、（31，1） D 、（31，－1） 2．若y=(a-3)x+a ²-9是正比例函数，则它的图像一定经过点……………（ ）A 、（1，-12）B 、(-1,6)C 、(-1,-6)D 、（-2，-6） 三、根据图象写出解析式1、、四、解答题1、已知直线y ＝kx 过点（－2，3），A 是直线y ＝kx 上一点，点B 的坐标为（4，0），且S △AOB=12，求点A 的坐标.2、正比例函数图像经过P （－3，2）和Q （－m ，m －1）（1）写出正比例函数解析式 （2）并求出m 的值，写出Q 点的坐标 （3）当x 取何值时，y>-13、如图是甲、乙两人的行程函数图，根据图像回答：⑴谁走得快？⑵求甲、乙两个函数解析式,并写出自变量的取值范围.⑶当t = 4时，甲、乙两人行程相差多少？∠1=∠2。

18.2正比例函数的图像（第2课时）（作业）（夯实基础+能力提升）【夯实基础】一、单选题1．（2021·上海市洋泾菊园实验学校八年级期末）直线23y x =-不经过点（ ） A ．（0，0） B ．（﹣2，3） C ．（3，﹣2） D ．（﹣3，2）2．（2021·上海市罗星中学八年级期中）关于函数y ＝﹣2x ，以下说法错误的是（ ）A ．图象经过原点B ．图象经过第二、四象限C ．图象经过点(2,2)-D ．y 的值随x 的增大而增大二、填空题3．（2021·上海市建平实验中学八年级期末）如果正比例函数y ＝（k ﹣2）x 的图象经过第二、四象限，那么k 的取值范围是 _____．4．（2020·上海市浦东模范中学八年级期末）已知正比例函数的图像经过点（2，-6），则这个函数的解析式为__________．5．（2022·上海·八年级期末）正比例函数(1)y k x =+图像经过点（1，-1），那么k =__________． 6．（2022·上海·八年级期末）已知正比例函数()0y kx k =≠的图象经过第一、三象限，且经过点（k ，k +2），则k =________．7．（2021·上海市蒙山中学八年级期中）正比例函数12y x =的图像经过第 ___象限． 三、解答题8．（2021·上海市蒙山中学八年级期中）已知如图，在平面直角坐标系中，点A （3，7）在正比例函数图像上．（1）求正比例函数的解析式．（2）点B （1，0）和点C 都在x 轴上，当△ABC 的面积是17.5时，求点C 的坐标．9．（2021·上海·八年级期中）已知y与x成正比例，且当x=12时，y=2，求（1）y关于x的函数解析式？（2）当y=-2时，x的值？【能力提升】一、单选题1．（2021·广东·深圳市南山外国语学校八年级期中）如图，正比例函数y＝kx，y＝mx，y＝nx在同一平面直角坐标系中的图象如图所示，则比例系数k，m，n的大小关系是（）A．n＜m＜k B．m＜k＜n C．k＜m＜n D．k＜n＜m2．（2022·全国·八年级专题练习）如果一个正比例函数的图象经过不同象限的两点A（3，m）、B（n，﹣2），那么一定有（）A．m＞0，n＞0 B．m＞0，n＜0 C．m＜0，n＞0 D．m＜0，n＜03．（2022·福建漳州·八年级期中）如图，9个边长为1的正方形摆放在平面直角坐标系中，经过原点的直线l将九个正方形组成的图形面积分为1：2的两部分，则该直线的解析式为（）A．12y x=B．109y x=1-C．12y x=或910y x=D．12y x=或109y x=二、填空题4．（2022·福建龙岩·八年级期中）若函数()21m y m x =-是关于x 的正比例函数，则该函数的图像经过第______象限．三、解答题5．（2020·四川巴中·八年级期末）如图，正方形ABCD 的边长为4，P 为边DC 上的一点，设DP x =，求APD △的面积y 与x 之间的函数关系式，并画出这个函数的图象．6．（2021·全国·八年级课时练习）画出下列正比例函数的图象：（1）12,3y x y x ==； （2） 1.5,4y x y x =-=-．7．（2022·福建·厦门市湖滨中学八年级期中）已知函数y =12x ，请按要求解决下列问题：(1)在平面直角坐标系中画出图象；(2)点（m －1，m ）在函数y =12x 的图象上，求m 的值．8．（2022·广东东莞·八年级期末）水是生命之源，节约用水是每个公民应尽的义务．水龙头关闭不严会造成滴水，为了调查水量与漏水时间的关系，某同学在滴水的水龙头下放置了一个能显示水量的容器，每5min 记录一次容器中的水量如下表： 时间/min t 0 5 10 15 20 …水量/mL v 0 25 50 75 100 …(1)请根据上表中的信息，在图中描出以上述实验所得数据为坐标的各点；(2)根据（1）中各点的分布规律，求出v 关于t 的函数解析式；(3)请估算这种漏水状态下一天的漏水量．9．（2021·上海·八年级期中）已知y 与x ﹣1成正比例，且当x=3时，y=4．（1）求y 与x 之间的函数表达式；（2）当x=﹣1时，求y 的值；（3）当﹣3＜y ＜5时，求x 的取值范围．10．（2020·上海市静安区实验中学八年级课时练习）正比例函数23m y mx -=的图象经过第一、三象限，求m的值．。