正比例函数的图像和性质

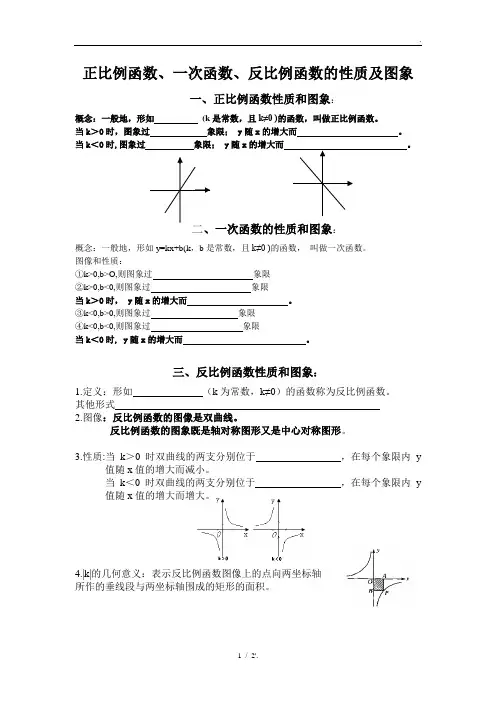
正比例函数、一次函数、反比例函数的性质及图象一、正比例函数性质和图象：概念：一般地，形如(k是常数，且k≠0 )的函数，叫做正比例函数。

当k＞0时，图象过象限； y随x的增大而。

当k＜0时,图象过象限； y随x的增大而。

：概念：一般地，形如y=kx+b(k，b是常数，且k≠0 )的函数，叫做一次函数。

图像和性质：①k>0,b>O,则图象过象限②k>0,b<0,则图象过象限当k＞0时， y随x的增大而。

③k<0,b>0,则图象过象限④k<0,b<0,则图象过象限当k＜0时, y随x的增大而。

三、反比例函数性质和图象：1.定义：形如（k为常数，k≠0）的函数称为反比例函数。

其他形式2.图像：反比例函数的图像是双曲线。

反比例函数的图象既是轴对称图形又是中心对称图形。

3.性质:当k＞0时双曲线的两支分别位于，在每个象限内y值随x值的增大而减小。

当k＜0时双曲线的两支分别位于，在每个象限内y 值随x值的增大而增大。

4.|k|的几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积。

练习题 1、若y =(m －1)x22m -是正比例函数，则m 的值为（ ） A 、1 B 、－1 C 、1或－1 D 、2或－2 2、下列函数中，一次函数为（ ）A 、25y x = B ．25y x =－1 C ．245y x = D ．25y x=-3、下列函数中，反比例函数是（ ）A 、y=x+1B 、y=C 、=1D 、3xy=24、正比例函数y=kx （k ≠0）函数值y 随x 的增大而增大，则y=kx+k 的图象大致是（ ）5、直线443--=x y 与两坐标轴围成的三角形面积是（ ） A 3 B 4 C 12 D 66、函数y 1=kx 和y 2=的图象如图，自变量x 的取值范围相同的是（ ）7、若点A(x 1,1)、B(x 2,2)、C(x 3,－3)在双曲线上，（ ）A 、x 1>x 2>x 3B 、x 1>x 3>x 2C 、x 3>x 2>x 1D 、x 3>x 1>x 28、已知一次函数y=ax+b 图象在一、二、三象限，则反比例函数y=的函数值随x 的增大而__________。

正比例函数的图像和性质
正比例函数是指函数的值与自变量成正比关系的函数，通常表示为y=kx，其中k为比例常数。

正比例函数的图像是一条经过原点的直线。

这是因为当自变量为0时，函数的值也为0，所以直线经过原点。

正比例函数的性质包括：
1. 随着自变量的增大，函数的值也随之增大或减小；随着自变量的减小，函数的值也随之减小或增大。

2. 自变量为0时，函数的值为0，即函数通过原点。

3. 函数的图像是一条经过原点的直线。

4. 如果k>0，则函数是递增函数；如果k<0，则函数是递减函数。

5. 函数的图像在第一象限和第三象限的部分为正值，而在第二象限和第四象限的部分为负值。

6. 正比例函数的图像是关于原点对称的，即改变自变量的正负会导致函数的正负改变。

值得注意的是，正比例函数的定义域和值域都可以是整个实数集合。

正比例函数的图像和性质知识精要1.正比例函数的图像一般地，正比例函数y=kx（k是常数，k0≠）的图像是经过原点O(0,0)和点M（1，k）的一条直线。

我们把正比例函数y=kx的图像叫做直线y=kx。

2.正比例函数性质精讲名题例1.若函数y=(m-1)3-mx是正比例函数，则m= ,函数的图像经过象限。

解:m=4,图像经过第一、三象限。

例2.已知y-1与2x成正比例，当x=-1时，y=5,求y与x的函数解析式。

解：∵y-1与2x成正比例∴设y-1=k·2x （k0≠）把x=-1,y=5代入，得k=-2,∴y-1=-2·2x∴y=-4x+1例3.已知y与x的正比例函数，且当x=6时y=-2(1)求出这个函数的解析式；(2)在直角坐标平面内画出这个函数的图像；(3)如果点P （a ，4）在这个函数的图像上，求a 的值；(4)试问，点A （-6，2）关于原点对称的点B 是否也在这个图像上？解：(1) 设y=k ·x （k 0≠）当x=6时，y=-2∴-2=6k ∴31-=k ∴这个函数的解析式为x y 31-=(2) x y 31-=的定义域是一切实数，图像如图所示：(3)如果点P （a ，4）在这个函数的图像上，∴a 314-=，∴a=-12(4)点A （-6，2）关于原点对称的点B 的坐标（6，-2），当x=6时，y=2631-=⨯- 因此，点B 也在直线x y 31-=上例4.已知点(11,y x )，(22,y x )在正比例函数y=(k-2)x 的图像上，当21x x >时，21y y <，那么k 的取值范围是多少？解：由题意，得函数y 随x 的值增大而减小，∴k-2<0,∴k<2例5.（1）已知y=ax 是经过第二、四象限的直线，且3+a 在实数范围内有意义，求a 的取值范围。

（2）已知函数y=(2m+1)x 的值随自变量x 的值增大而增大，且函数y=(3m+1)x 的值随自变量x 的增大而减小，求m 的取值范围。

第十九章一次函数19.2 一次函数19.2.1 正比例函数第2课时正比例函数的图象与性质教学设计【探究1】用描点法画出正比例函数y = 2x的图象.练习：在同一直角坐标系中用描点法画岀正比例函数y=3x的图象.3思考：对一般正比例函数y= kx,当k> 0时，它的图象形状是怎样的？位置呢？在k>0的情况下，图象是左低右高还是左高右低？当自变量的值增大时，对应的函数值是增大还是减小？【探究2】当k v0时，正比例函数的图象特征及性质又怎样呢？请各小组画出函数y= —3x和y=—1.5x的图象，小组间进行合作研究.［师生活动］让学生在完成上述练习的基础上总结归纳岀正比例函数解析式与图象特征之间的规律：正比例函数y= kx（k是常数，k工0）的图象是一条经过原点的直线. 当k>0时，图象经过第一、三象限，从左向右上升，即随着x的增大y 也增大；当k<0时，图象经过第二、四象限，从左向右下降，即随着x 的增大y反而减小.正是由于正比例函数y= kx（k是常数，k工0）的图象是一条直线，我们可以称它为直线y= kx.【探究3】正比例函数的图象是一条经过坐标原点的直线，我们知道，两点确定一条直线，现在，你知道画正比例函数图象的简便方法了吗？［师生活动］教师引导学生用简便方法画正比例函数的图象.用你认为最简单的方法画出下列函数的图象：(1)y = ；x; (2)y = —3x.活动实践探究交流新知让学生观察、分析、讨论、对比图象的异同：发现函数图象的性质.在多个实例的基础上,归纳得到正比例函数图象的性质，潜移默化地对学生渗透了概括、归纳、比较、分析等数学思想方法.［学生活动］学生合作探究交流得出结论：画正比例函数的图象时，只需在原点外再确定一个点，即找岀一组 满足函数解析式的对应数值即可，如（1, k ）,因为两点可以确定一条直线例 在同一直角坐标系中，画岀下列函数的图象，并对它们进行比 较.1 1(1)y = 2x ; (2)y = - 2x.图 19- 1 -［师生活动］比较两个函数图象可以看出： 两个图象都是经过坐标原点1的直线.函数y = 2x 的图象从左向右上升，经过第一、三象限，即随着x1的增大y 也增大；函数y =— -x 的图象从左向右下降，经过第二、四象 限，即随着x 的增大y 反而减小. 【应用举例】例1汽车由天津驶往相距120千米的北京，s （千米）表示汽车离开 天津的距离，t （时）表示汽车行驶的时间，s 与t 之间的关系如图19-2-7活动实践 探究 交流 新知教师引导学生用简 便方法画正比例函数的 图象，并利用此例让学 生巩固正比例函数图象 的性质.活动开放训练体现应用图19-2 - 7活动开放训练体现应用(1) 汽车用几小时可到达北京？速度是多少？(2) 汽车行驶1小时，离开天津有多远？(3) 当汽车距北京20千米时，汽车岀发了多长时间？解法一：用图象解答：(1) 从图上可以看出汽车用4个小时可到达北京.120速度=~4~ = 30(千米/时).(2) 汽车行驶1小时离开天津约为30千米.(3) 当汽车距北京20千米时，汽车出发了约3.3小时. 解法二：用解析式来解答：(1)由图象可知：s与t是正比例关系，设s= kt，当t = 4 时，s= 120，即120 = k x4，k= 30，•*s= 30t.(1) 汽车4小时可达到北京，速度为30千米/时.(2) 当t= 1 时，s= 30X1 = 30(千米).10(3) 当s= 100 时，100= 30t，t= 3 (时).3以上两种方法比较，用图象法解题直观，用解析式解题准确，各有优点.【拓展提升】ty图19-2-8例2观察图象比较大小：(1) k1__ =_k2；(2) k3__<.__k4；(3) 比较k1，k2，k3，k4的大小，并用不等号连接.[答案：k1< k2< k3< k4]变式训练1.当k>0时，正比例函数y= kx的图象大致是(A )A B C D图19-2-92.已知正比例函数y = (3k- 1)x，y随着x的增大而增大，则k的取值范围是(D )1 1A.k< 0B.k> 0C.k< 3D.k >3应用迁移、巩固提高，培养学生解决问题的能力.1•知识的综合与拓展，提高应考能力.2.进一步使学生巩固正比例函数的性质使学生体验数形结合思想的运用过程.。

第九讲 一次（正比例）图像及其性质目录必备知识点........................................................................................................................................1考点一 函数的概念理解................................................................................................................1考点二 一次函数概念的理解........................................................................................................4考点三 一次函数图像....................................................................................................................5考点四 一次函数图像性质1.........................................................................................................9考点五 一次函数图像性质2. (13)必备知识点知识点1 正比例函数图像（y=kx ）1.正比例函数图像是一条经过原点的直线。

2.性质（1）正比例函数图像必过（2）k>0，函数图像经过 象限，y 随x 的增大而 （3）K<0，函数图像经过 象限，y 随x 的增大而知识点2 一次函数图像（y=kx+b ）1.一次函数图像是一条直线。