结构力学E第3次作业

第1次作业（结构力学二）一、单项选择题（本大题共40分，共 20 小题，每小题 2 分）1. 位移法的基本结构是( )A. 静定刚架；B. 单跨静定梁的组合体；C. 单跨超静定梁的组合体D. 铰结体系2. ：以下关于影响线的说法不正确的一项为( )A. 影响线指的是单位力在结构上移动时所引起的结构的某一内力(或反力)变化规律的图形B. 利用影响线可以求结构在固定荷载作用下某个截面的内力C. 利用影响线可以求结构某个截面内力的最不利荷载位置D. 影响线的横坐标是截面位置，纵坐标为此截面位置处的截面内力值3.A. B. C. D. 仅由平衡条件不能确定4. 不计杆的分布质量，图示体系的动力自由度为( )A. 1；B. 2；C. 3；D. 45. 用力法计算超静定结构时，其基本未知量为A. 杆端弯矩；B. 结构角位移；C. 结点线位移；D. 多余未知力6. 单元坐标转换矩阵是（） A. 奇异矩阵 B. 对称三对角矩阵 C. 对称非奇异矩阵 D. 正交矩阵7. 位移法的基本未知量包括（）A. 独立的角位移B. 独立的线位移C. 独立未知的结点角位移和线位移D. 结点位移8. 图乘法计算位移的公式中( )A. A和yC 可取自任何图形B. A和yC必须取自直线图形C. 仅要求A必须取自直线图形D. 仅要求yC必须取自直线图形9. 已知材料屈服极限 =300MPa,结构截面形状如图所示，则极限弯矩Mu=（）A. 20kN•mB. 25kN•mC. 30kN•mD. 35kN•m.10. 整体坐标系下单元刚度矩阵与下面的哪一个因素无关A. 局部坐标与整体坐标的选取B. 结构的约束信息C. 单元的几何参数D. 杆端位移与杆端力之间的变换关系11. 欲减小图示结构的自振频率，可采取的措施有（）A. 减小质量mB. 增大刚度EIC. 将B支座改为固定端D. 去掉B支座12. 图（b）为图（a）所示结构MK影响线，利用该影响线求得图（a）所示固定荷载作用下的MK值为（）A. 4kN•mB. 2kN•mC. -2kN•mD. -4kN•m13. 图示为三自由度体系的振型，其相应的频率是ωa 、ωb、ωc，它们之间的大小关系应是( )A. B. C. D.14. 图（a）所示一组移动荷载作用在图（b）所示的梁上，则C截面弯矩的最不利位置为（）A. P1作用在C点上 B. P2作用在C点上 C. P3作用在C点上 D. P3作用在B点上15. 平面杆件自由单元(一般单元)的单元刚(劲)度矩阵是( )A. 非对称、奇异矩阵B. 对称、奇异矩阵C. 对称、非奇异矩阵D. 非对称、非奇异矩阵16. 对称结构在反对称荷载作用下，内力图中为正对称的是( )A. 弯矩图B. 剪力图C. 轴力图D. 弯矩图、剪力图和轴力图17. 由于温度改变，静定结构（） A. 会产生内力，也会产生位移； B. 不产生内力，会产生位移； C. 会产生内力，不产生位移； D. 不产生内力，也不产生位移。

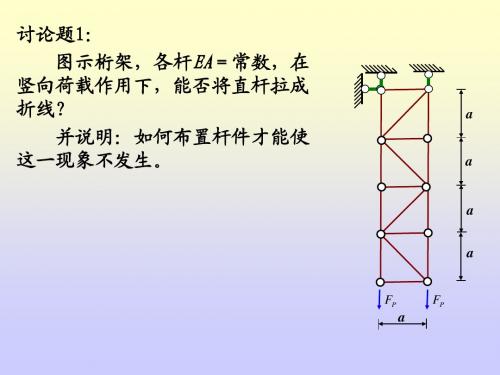
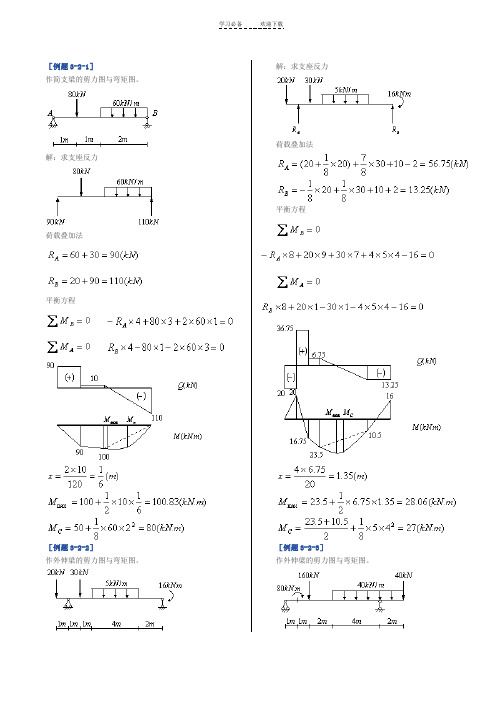
［例题3-2-1］作简支梁的剪力图与弯矩图。

解：求支座反力荷载叠加法平衡方程［例题3-2-2］作外伸梁的剪力图与弯矩图。

解：求支座反力荷载叠加法平衡方程［例题3-2-3］作外伸梁的剪力图与弯矩图。

解：求支座反力荷载叠加法平衡方程［例题3-3-1］作多跨静定梁的内力图。

解：求支座反力荷载叠加法［例题3-3-2］作三跨静定梁的内力图。

解：求支座反力［例题3-3-3］ 作多跨静定梁的内力图。

解：求支座反力［例题3-4-1］ 作静定刚架的内力图解：求支座反力［例题3-4-2］作静定刚架的内力图解：求支座反力［例题3-4-3］作静定刚架的内力图解：求支座反力［例题3-4-4］作静定刚架的内力图解：求支座反力［例题3-4-5］作三铰刚架的内力图解：求支座反力［例题3-4-6］作三铰刚架的内力图解：求支座反力??［例题3-4-7］作静定刚架的内力图解：求支座反力［例题3-4-8］作静定刚架的图解：［例题3-4-9］作静定刚架的图解：［例题3-4-10］作静定刚架的图解：［例题3-4-11］作静定刚架的图解：［例题3-4-12］作静定刚架的图解：［例题3-4-13］作静定刚架的图解：［例题3-4-14］作静定刚架的图解：求支座反力?［例题3-4-15］作静定刚架的图解：［例题3-5-1］???求支座反力当时?????? ? ?????学习必备欢迎下载［例3-5-2］??? 试求对称三铰拱在竖向均布荷载作用下的合理轴线。

解：相应简支梁的弯矩方程为水平推力合理轴线方程为合理轴线为一抛物线。

［例3-6-1］用结点法求桁架各杆的内力。

解：求支座反力解题路径：以结点为对象以结点为对象以结点为对象以结点为对象［例3-6-2］用结点法求桁架各杆的内力。

解：求支座反力平衡方程荷载叠加法解题路径：以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象以结点为对象［例3-6-3］用结点法求桁架各杆的内力。

解：利用对称性，求支座反力解题路径：以结点为对象?以结点为对象以结点为对象以结点为对象例3-6-4］指出桁架的零杆。

第一章结构的几何构造分析六、练习题1.二元体规律1-1试对图1-59所示平面体系进行几何组成分析。

(南京工业大学2019)(b)a)(c)图1-59图1-60图1-611-2对图1-60所示体系进行几何组成分析。

（天津大学2017）1-3对图1-61所示体系作几何组成分析。

（苏州科技大学2016）1-4对图1-62所示平面体系进行几何组成分析，并指出超静定次数。

（青岛理工大学2016）图1-62图1-63图1-641-5对图1-63所示体系作几何组成分析。

（东南大学2014）2.两刚片规律1-6试对图1-64所示平面体系进行几何组成分析。

(南京工业大学2019)1-7对图1-65（a ）（b ）所示体系进行几何构造分析。

（青岛理工大学2019）图1-65图1-661-8求图1-66所示体系的计算自由度,并进行几何组成分析。

（华南理工大学2017）1-9对图1-67所示体系作几何组成分析。

（苏州科技大学2018、中国矿业大学2014、吉林建筑工程学院2013）图1-67图1-68图1-69 1-10图1-68所示体系的机动分析结论是。

（重庆交通大学2015）3.三刚片规律3.1三个铰都对应于有限点1-11对图1-69所示平面体系进行几何组成分析。

(南京工业大学2019)1-12对图1-70所示体系进行几何组成分析(各点均为铰结点)。

(长沙理工大学2017)图1-70图1-71 1-13图1-71所示体系的计算自由度W=，有个多余约束，为体系。

（哈尔滨工业大学2017）1-14试对图1-72所示平面体系进行几何组成分析。

（哈尔滨工业大学2015）图1-72图1-73图1-74 1-15计算图1-73所示杆件体系的计算自由度，并判断体系符合哪种几何组成规律？（北京工业大学2014）3.2一个无穷远瞬铰1-16对图1-74所示体系进行几何构成分析。

（西安交通大学2015）1-17图1-75所示为（）。

（山东科技大学2018）A.无多余约束的几何不变体系；B.有多余约束的几何不变体系；C.瞬变体系；D.常变体系。

《结构力学习题》(含答案解析)-CAL-FENGHAI.-(YICAI)-Company One120 第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.M C.=1=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M kM p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

Aa a21 9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数 ，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数 。

l l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

q15、求图示刚架结点C 的转角和水平位移，EI = 常数 。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l ll/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

E I = 常数。

qll l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。

第一次作业一、画出前后面应力二、列出Z 向平衡方程Z 向应力：z σ、zx τ、zy τz z dz z σσ∂+∂、zx zx dx x ττ∂+∂、zy zy dy yττ∂+∂ Z 向平衡方程：()()()0zy z zx z zx zy z zx zy dz dxdy dx dydz dy dxdz dxdy dydz dxdz Zdxdydz z x y τστσττσττ∂⎡⎤∂∂⎡⎤+++++-+++=⎢⎥⎣⎦∂∂∂⎣⎦化简得：0zyz zx Z z x yτστ∂∂∂+++=∂∂∂三、写出平面应力问题的几何方程和物理方程各项同性体几何方程：x xy y yz z xz u u v x y x v v wy z z w u wz z x εγεγεγ∂∂∂⎧==+⎪∂∂∂⎪⎪∂∂∂==+⎨∂∂∂⎪⎪∂∂∂==+⎪∂∂∂⎩各项同性体物理方程：11()11()11()x x y z xy xy y y z x yz yz zz x y xz xz E GE G E G εσυσσγτεσυσσγτεσυσσγτ⎧⎡⎤=-+=⎪⎣⎦⎪⎪⎡⎤=-+=⎨⎣⎦⎪⎪⎡⎤=-+=⎪⎣⎦⎩其中：2(1)E G υ=+ 平面应力问题时：0,0,0z yz xz σττ===则物理方程：1()1()1x x y y y x xy xy E E G εσυσεσυσγτ⎧⎡⎤=-⎪⎣⎦⎪⎪⎡⎤=-⎨⎣⎦⎪⎪=⎪⎩或1()1()2(1)x x y y y x xy xyE E E εσυσεσυσυγτ⎧⎡⎤=-⎪⎣⎦⎪⎪⎡⎤=-⎨⎣⎦⎪⎪+=⎪⎩几何方程：x y xy u x vy u vy x εεγ⎧∂=⎪∂⎪⎪∂=⎨∂⎪⎪∂∂=+⎪∂∂⎩四、要使下列应变分量成为一种可能的应变状态，试确定常数A0、A1、B0、B1、C0、C1、C2之间的关系。

22440122440122012()()()()()x y xyA A x y x yB B x y x yC C xy x y C εεγ⎧=++++⎪=++++⎨⎪=+++⎩ 由：224401()()x uA A x y x y xε∂==++++∂ 得：325401111()35u A x A x A y x x y x D y =+++++ （1）由：224401()()y vB B x y x y y ε∂==++++∂得：234501111()35v B y B x y B y x y y D x =+++++ （2）由已知条件：22012()xy u vC C xy x y C y x γ∂∂=+=+++∂∂将（1）（2）代入上式，得：332211012()()2244()u v D y D x A yx B xy y x x y C C xy x y C y x y x∂∂∂∂+=+++++=+++∂∂∂∂ 整理得：22221101211()()4()()22D y D x yx y x A B C C xy x y C y x∂∂+++++=+++∂∂ 最终：111241122C A B C =⎧⎪⎨+=⎪⎩第二次作业2-5图2-15所示简支梁。