下载文档原格式
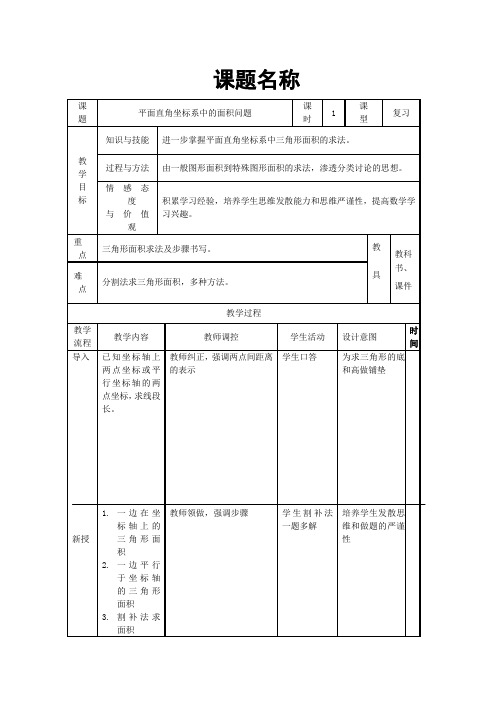
平面直角坐标系中的面积问题
广州市天河外国语学校陈玲萍
一、教学目标
1.进一步掌握平面直角坐标系中已知点的坐标求面积的问题；
2.渗透转化思想；
3.培养学生的思维发散能力，同时培养学生思维的严谨性，提高数学学习的兴趣。
二、教学重难点
教学重点：在平面直角坐标系中已知点的坐标求图形的面积
教学难点：将不规则图形进行适当的割补，转化为规则图形求面积
三、教学过程
轴的边作为底，方便找底、高的长度。
，
分割成一个直角梯形和一个直角三角形；
④过B点做y轴的垂线，过A点做x轴的垂线，将四边形ABCO补成一个长方形。
【设计意图】由问题3三角形的面积求法迁移到求四边形的面积，进而理解多边形面积的求法都类似。
【分析】（1）B （8,4），C （8,0） （2）连接OB
由题意，t 秒时，OQ =t CP =2t ∴OP =8-2t
∴BO P BO Q O PBQ S S S ∆∆+=四边形
=
BC OP AB OQ ∙+∙21
21 =
()t t 2842
1
821-∙∙+∙。
在平面直角坐标系中求几何图形的面积邯郸市汉光中学蒋朝杰教材分析：本节课内容是在学生掌握了平面直角坐标系中已知坐标求线段长度。
点的坐标到坐标轴或平行于坐标轴直线的距离的知识。
在在此基础上学习本节课内容。
培养学生从特殊到一般的思维能力和推理能力等方面有重要的作用。
通过在平面直角坐标系中求三角形和四边形面积。
初步掌握已知坐标求面积的方法和技能。
从特殊到一般和数形结合数学思想方法是今后研究数学的基本思想方法。
在以后学习一次函数和二次函数中已知坐标求面积做好基础，起着承前启后的作用。
学情分析：学生在学习本课之前已经学过了在平面直角坐标系中求坐标轴上两点距离、平行于坐标轴的直线上两点的距离线段。
点到坐标轴的距离。
这节课是已知坐标求面积的习题课。
只是学生的分析能力、归纳概括能力仍相对薄弱，学习过程中，可能有一部分学生方法不全面，教师要适时加以点拨和指导。
学习目标：知识技能：会在平面直角坐标系中已知坐标求几何图形面积。
过程方法：让学生经历把“平面中的不规则图形转化为规则图形”的方式求出平面图形的面积的过程，体验图形结合思想，着力培养学生一题多解的能力。
情感态度：努力发展学生分析处理数学问题的能力。
重点、难点重点：在平面直角坐标系中已知坐标求几何图形面积。
难点：利用割补法求不规则图形的面积。
教法学法：教法设想：我采用讲练结合教学法完成本节的教学，在教学中通过设计问题，引导学生自主探索，合作交流，有效地启发学生的思考，使学生真正成为学习的主体。
学法设计：在学生学习的过程中，我将从两个方面指导学生学习，一方面老师大胆放手，让学生去自主探究各种求面积的方法，另一方面，在三角形和四边形图形求面积时，老师要巧妙引导用割补法求面积，分散难点。
这样做既有利于活跃学生的思维，又能帮助他们探本求源，这样也体现了以“教师为主导，学生为主体”的新课改背景下的教学原则。
教学流程：【知识回顾】（1）在平面直角坐标系中，点P（a,b)到x轴的距离等于到y轴的距离等于（2）若P(a,b),Q(a,c),M(d,b),则PM∥轴，PQ ∥轴，MP长为 ,PQ长为设计目的：整节课的课前热身活动，必须掌握根据坐标求线段的长。
《专题：在平面直角坐标系中的面积问题》教学设计广州市番禺区洛浦沙滘中学刘永思【教材分析】1.教学内容：①在平面直角坐标系中利用三角形的顶点坐标求三角形的面积；②利用三角形的面积求顶点坐标。
2.平面直角坐标系具有较强的基础性，它是进一步研究和解决其他问题的基础，特别是以后我们学习函数的基础，是中考的重要内容。
3.平面直角坐标系中的应用很好地体现了数形结合的思想，在关于求点的坐标的题型中往往会出现情况不确定需要进行分类讨论的情况，渗透了数学的分类讨论的思想。
在学习知识之余，对学生的思维也起到了很好的训练作用。
【学情分析】平面直角坐标系是后续学习的重要工具，但七年级的学生由于刚接触，对于点的位置和坐标的关系理解和应用还不是很熟悉。
利用点的坐标求两点间的距离的应用可以让学生进一步熟悉平面直角坐标系的应用，而结合三角形的面积问题求点的坐标，综合性较强，但对于提升学生的能力有很大的帮助，并能为八年级函数的应用打下更好的基础。
【学习目标】1.会在平面直角坐标中求简单的两点间的距离，如在坐标轴上的两点，或者连线平行于坐标轴的两点，以及点到坐标轴的距离。
2.在平面直角坐标系中能利用点的坐标求三角形的面积，能利用三角形的面积求点的坐标，体现数形结合的重要作用。
3.在解决平面直角坐标系中的问题时，要学会把较生僻、繁琐的问题化归为较简单、熟悉的问题，从而使问题轻而易举得以解决。
在探索求点的坐标过程中，引导学生把求点的坐标转化为熟悉的三角形面积问题的已知题型，化解解题的障碍，感悟转化思想。
【学习重难点】重点：会利用点的坐标求两点间的距离（或是线段的长度）；会利用三角形的面积公式求点的坐标。
难点：①设点的坐标，通过面积关系建立方程求出点的坐标，利用方程思想解决问题，对于七年级学生具有一定的难度；②在解决点的坐标中，由于未能确定未知数的符号要带上绝对值符号，对于学生的理解来说有较高的欢度；③在求点的坐标中，如何根据情况的不确定，恰当进行分类论。
