云南省蒙自县文澜高级中学2014届高三10月月考数学(文)试题

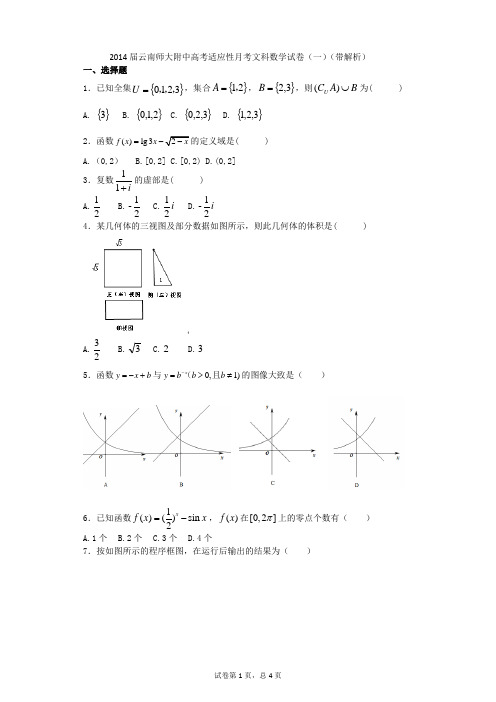
2014届云南师大附中高考适应性月考文科数学试卷（一）（带解析） 一、选择题1．已知全集{}3210，，，=U ，集合{}21，=A ，{}3,2=B ，则B A C U ⋃)(为( ) A. {}3 B. {}2,1,0 C. {}3,2,0 D. {}3,2,12．函数()lg3f x x =-的定义域是( ) A.（0,2） B.[0,2] C.[0,2) D.(0,2]3．复数i +11的虚部是( ) A.21 B.21- C.i 21 D.i 21- 4．某几何体的三视图及部分数据如图所示，则此几何体的体积是( )C.2D.35．函数y x b =-+与0,1)xy b b b -=>≠（且的图像大致是（ ）6．已知函数1()()sin 2xf x x =-，()f x 在[0,2]π上的零点个数有（ ） A.1个 B.2个 C.3个 D.4个7．按如图所示的程序框图，在运行后输出的结果为（ ）A.66B.65C.55D.468．命题:,3xp x R x ∀∈>；命题:(3)q y f x =-若函数为奇函数 , 则()y f x =函数的图像关于点3,0（）成中心对称，下列命题正确的是（ ） A.p q ∨真 B.p q ∧真 C.q ⌝真 D.p ⌝假()f x (+4)=()f x f x (4)()f x f x +=[2,0)x ∈-2()=-2f x x (2013)f10．将函数()4sin(2)4f x x π=-+的图像向右平移ϕϕ(>0)个单位，再将图像上每一点的横坐标缩短到原来的12倍，所得图像关于直线4x π=，则ϕ的最小正值为（ ） A.8πB.38πC.2πD.34π二、填空题11．已知R 上可导函数()f x 的图像如图所示，则不等式2(23)()0x x f x '-->的解集为（ ）A.(,1)(3,)-∞-⋃+∞B.--2∞⋃（，）（1,2）C.(,1)-1,0(2,)-∞-⋃⋃+∞（）D.(,1)-1,1(3,)-∞-⋃⋃+∞（）12．已知函数2log ,0,()3,0,x x x f x x >⎧⎪=⎨⎪⎩≤，则14ff ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦． 13．已知1tan 3x =，则cos 2x = ． 14．曲线3()2f x x x =+-在0P 处的切线平行于直线41y x =-，则0P 坐标为 15．在三棱锥S −ABC中，,2AB BC AB BC SA SC ====⊥，二面角S −AC −B 的余弦值，若S 、A 、B 、C 都在同一球面上，则该球的表面积是 ．三、解答题16．已知函数21()cos cos ,2f x x x x x R =--∈．（Ⅰ）求函数()f x 最大值和最小正周期；（Ⅱ）设ABC ∆的内角A C 、B 、的对边分别为a c 、b 、，且3,()0c f C ==，若sin()2sin A C A +=,求a 、b 的值17．如图，在四棱锥-P ABCD 中，四边形ABCD 是菱形，PA PC =,E 为PB 的中点．（Ⅰ）求证：PD ∥平面AEC ；（Ⅱ）求证：平面AEC ⊥平面PBD .18．已知一家公司生产某种产品的年固定成本为10万元，每生产1千件该产品需另投入 2.7万元，设该公司一年内生产该产品x 千件并全部销售完，每千件的销售收入为()R x 万元，且22110.8,010,30)1081000,10.3x x R x x xx ⎧-<⎪⎪=⎨⎪->⎪⎩≤（ （Ⅰ）写出年利润W （万元）关于年产量x （千件）的函数解析式；（Ⅱ）年产量为多少千件时，该公司在这一产品的产销过程中所获利润最大． 19．已知函数1ln ()xf x x+=． （Ⅰ）若函数在区间1,(0)2t t t ⎛⎫+> ⎪⎝⎭其中上存在极值，求实数t 的取值范围；（Ⅱ）如果当1x ≥时，不等式()1af x x +≥恒成立，求实数a 的取值范围． 20．如图，已知圆⊙O 1与圆⊙O 2外切于点P ，过点P 的直线交圆⊙O 1于A ，交圆⊙O 2于B ，AC 为圆⊙O 1直径，BD 与⊙O 2相切于B ，交AC 延长线于D ．（Ⅰ）求证：AD BD ⊥；（Ⅱ）若BC 、PD 相交于点M,则AP BM AD PM = ．21．以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为：=2cos()3πρθ-，曲线C 2的参数方程为：4cos cos 3(0)2sin sin 3x t t y t πααπα⎧=+⎪⎪>⎨⎪=+⎪⎩为参数，，点N 的极坐标为(4)3π，．（Ⅰ）若M 是曲线C 1上的动点，求M 到定点N 的距离的最小值； （Ⅱ）若曲线C 1与曲线C 2有有两个不同交点，求正数t 的取值范围．22．若a b x y 、、、均为正实数，并且+=1x y ，求证：2()()().4a b ab ax by ay bx +++≤≤2014届云南师大附中高考适应性月考文科数学试卷（一）（带解析）参考答案 1．C 【解析】试题分析：{}30，=A C U ，}320{)(，，=⋃B A C U 故选C ． 考点：集合的并集运算 2．D 【解析】试题分析：02,03≥->x x ,20≤<x 故选D ． 考点：函数的定义域,解不等式． 3．B 【解析】 试题分析：2-111-111i i i i i =+-=+））（（,复数i+11的虚部为21-，故选B ． 考点：复数的概念和运算4．A 【解析】故选A ． 考点：三视图和几何体的体积 5．C 【解析】试题分析：特殊值验证如取b=0.5，故选C ． 考点：一次函数、指数函数的图像 6．B 【解析】试题分析：（数形结合）函数()f x 在[0,2π]上的零点个数，由函数12xy ⎛⎫= ⎪⎝⎭与sin y x =的图象在[0,2π]上的交点个数为2，故选B ．考点：函数的零点7．B 【解析】试题分析：执行程序后，输出10(12310)+++++…，故选B ． 考点：算法的循环结构，程序框图 8．A 【解析】试题分析：∵p 命题是真命题，q 命题是假命题，故选A ．考点:复合命题的真假判定 9．C 【解析】试题分析：∵()f x 是R 上的奇函数，且满足(4)(),()f x f x f x +=∴是以4为周期的周期函数，易得当(0,2]x ∈时，22()2,(2013)(50341)(1)212f x x f f f ==⨯+=== ∴，故选C ． 考点：函数的性质 10．B 【解析】 试题分析：用排除法，π8ϕ=显然不对，若3π8ϕ=，则依题意有： π3π()4sin 224cos 248f x x x ⎛⎫=-+-⨯= ⎪⎝⎭→()4cos 4f x x =满足题设，故选B ．考点：导数的几何意义，倾斜角与斜率 11．D 【解析】 试题分析：由可导函数)(x f 的图象知，不等式2(23)()0x x f x '-->⇔2(23)(1)(1)0x x x x --+->不等式2(1)(1)(3)0x x x ⇔+-->，∴原不等式的解集为{}1,31x x x x <>≠-且，故选D ．考点：导数，不等式 12．19【解析】试题分析：由2log ,0,()3,0,x x x f x x >⎧⎪=⎨⎪⎩≤知14f f ⎡⎤⎛⎫= ⎪⎢⎥⎝⎭⎣⎦21(2)39f --==．考点：分段函数13．45【解析】试题分析：∵1tan 3x =，∴cos 2x =22111tan 4911tan 519x x --==++． 考点：三角函数求值 14．（1，0）或（−1，−4）． 【解析】试题分析：设0P 点的坐标为00(,)x y ，∵曲线3()2f x x x =+-在0P 处的切线平行于直线41y x =-，200()314f x x '=+=∴⇔201x =⇔01x =±，∴P 0点的坐标为（1，0）或（−1，−4）．考点：导数的几何意义． 15．6π 【解析】如图，取AC 的中点D ，由已知易证二面角S −AC −B 的平面角是∠SDB ，由勾股定理的逆定理可得,BS AB BS BC ⊥⊥，补体得正方体，∴三棱锥S −ABC ∴该球的表面积是6π．考点：立体几何的二面角，球的表面积16．（Ⅰ）()f x 的最大值为0，最小正周期是2ππ2T ==；（Ⅱ）a =b = 【解析】 试题分析：（Ⅰ）先化简()f x ，再求函数()f x 最大值和最小正周期；（Ⅱ）根据正弦定理化简sin()sin 2sin A C B A +==，由余弦定理得222π2cos 3c a b ab =+-，通过解方程求解答案．试题解析：（Ⅰ）1cos 21π()2sin 21226x f x x x +⎛⎫=--=-- ⎪⎝⎭， （3分） 则()f x 的最大值为0，最小正周期是2ππ2T ==．（5分） （Ⅱ）π()sin 2106f C C ⎛⎫=--= ⎪⎝⎭，则πsin 216C ⎛⎫-= ⎪⎝⎭. （6分）∵0πC <<，∴022πC <<，∴ππ112π666C -<-<， ∴ππ262C -=，∴π3C =． （7分） 又∵sin()sin 2sin A C B A +==，由正弦定理得12a b =，① （9分） 由余弦定理得222π2cos 3c a b ab =+-，即229a b ab +-=，②（10分）由①②解得a b = （12分）考点：三角变换、正弦定理、余弦定理 17．见详解 【解析】 试题分析：（Ⅰ）要证线面平行，需要找线线平行，根据线面平行的判定定理得证；（Ⅱ）要证面面垂直，需要线面垂直，根据面面垂直的判定定理得证；证明：（Ⅰ）如图，设AC BD O = ，连接EO ，因为O ，E 分别是BD ，PB 的中点，所以PD EO ∥， （4分） 而,PD AEC EO AEC ⊄⊂平面平面，所以PD ∥平面AEC .（6分）（Ⅱ）连接PO ，因为PA PC =，所以AC PO ⊥，又四边形ABCD 是菱形， 所以AC BD ⊥. （9分） 而PO ⊂平面PBD ，BD ⊂平面PBD ，PO BD O = ，所以AC ⊥平面PBD ， （11分）又AC ⊂平面AEC ，所以平面AEC ⊥平面PBD . （12分） 考点：线面平行，面面垂直18．（Ⅰ）38.110,010,30100098 2.7,10.3x x x W x x x ⎧--<⎪⎪=⎨⎪-->⎪⎩≤；（Ⅱ）当9x =时，W 取得最大值为38.6万元． 【解析】试题分析：（Ⅰ）利润W （万元）=销售收入-成本；（Ⅱ）利用导数分别求出分段函数的每一段的最大值，最后再求最大中的最大． 试题解析：解：（Ⅰ）当010x <≤时，3()(10 2.7)8.11030x W xR x x x =-+=--， （2分）当10x >时，1000()(10 2.7)98 2.73W xR x x x x=-+=--， （4分）∴38.110,010,30100098 2.7,10.3x x x W x x x ⎧--<⎪⎪=⎨⎪-->⎪⎩≤（6分）（Ⅱ）①当010x <≤时，由28.1010x W '=-=，得9x =．当(0,9)x ∈时，0W '>；当(9,10]x ∈时，0W '<，∴当9x =时，W 取得最大值，即3max 18.1991038.630W =⨯-⨯-=． （9分） ②当10x >时，100098 2.798383W x x ⎛⎫=-+-⎪⎝⎭≤， 当且仅当10002.73x x=，即1009x =时，W 取得最大值38．综合①②知：当9x =时，W 取得最大值为38.6万元， （11分） 故当年产量为9千件时，该公司在这一产品的产销过程中所获的年利润最大． （12分）考点：导数的实际应用，函数的最值 19．（Ⅰ）112t <<；（Ⅱ）2a ≤． 【解析】试题分析：（Ⅰ）先对函数求导，求出函数的极值，根据函数()f x 在区间1,(0)2t t t ⎛⎫+> ⎪⎝⎭其中上存在极值，所以1,11,2t t <⎧⎪⎨+>⎪⎩ 从而解得1 1.2t <<（Ⅱ）不等式()1a f x x +≥恒成立问题转化为求函数的最值问题． 试题解析：解：（Ⅰ）因为1ln (),0x f x x x +=>，则2ln ()xf x x'=-， （2分） 当01x <<时，()0f x '>；当1x >时，()0f x '<.所以()f x 在(0,1)上单调递增；在(1,)+∞上单调递减，所以函数()f x 在1x =处取得极大值. （4分）因为函数()f x 在区间1,(0)2t t t ⎛⎫+> ⎪⎝⎭其中上存在极值，所以1,11,2t t <⎧⎪⎨+>⎪⎩ 解得1 1.2t << （6分）（Ⅱ）不等式(),1a f x x +≥即为(1)(1ln ),x x a x ++≥ 记(1)(1ln )()x x g x x++=， 所以22[(1)(1ln )](1)(1ln )ln ()x x x x x x xg x x x'++-++-'==， （9分） 令()ln h x x x =-，则1()1h x x'=-， 1x ∵≥，()0h x '∴≥，()h x ∴在[1,)+∞上单调递增，min [()](1)10h x h ==>∴，从而()0g x '>，故()g x 在[1,)+∞上也单调递增，所以min [()](1)2g x g ==，所以2a ≤. （12分） 考点：函数与导数，函数极值与最值，不等式恒成立 20．见详解 【解析】 试题分析：（Ⅰ）根据切线的性质证明；（Ⅱ）由P 、B 、D 、C 四点共圆，又易证PCM BDM △∽△，即根据三角形相似得出相似比． 试题解析：证明：（Ⅰ）如图，过点P 作两圆公切线交BD 于T ，连接PC ，∵AC 为直径，90APC ∠=︒∴， 90BPC TPC TPB ∠=∠+∠=︒∴， 90A ACP ∠+∠=︒， 又BD 与⊙O 2相切于B ， PT 为两圆公切线，TPC A ∠=∠∴，TBP TPB ∠=∠， TPB ACP TBP ∠=∠=∠∴， 90A TBP ∠+∠=︒∴，故90,ADB AD BD ∠=︒∴⊥. （5分） （Ⅱ） 由（Ⅰ）易证APC △∽ADB △， ∴PC APBD AD=，又由（Ⅰ）知∠ACP=∠DBP ， ∴P、B 、D 、C 四点共圆，又易证PCM BDM △∽△，PC PMBD BM=∴，∴PM APBM AD=，∴AP BM AD PM = ． （10分）考点：圆的切线21．（Ⅰ）2；（Ⅱ）1,1)．【解析】试题分析：分别将极坐标方程与参数方程转化为普通方程，根据点与圆的几何意义求MN 的最小值；根据曲线C 1与曲线C 2有有两个不同交点的几何意义，求正数t 的取值范围． 试题解析：解：（Ⅰ）在直角坐标系xOy 中，可得点(2,N ，曲线1C 为圆22112x y ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭，圆心为11,2O ⎛ ⎝⎭，半径为1，∴1O N =3，∴MN 的最小值为312-=． （5分）答案第7页，总7页 （Ⅱ）由已知，曲线1C为圆22112x y ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭， 曲线2C为圆222(2)((0)x y t t -+=>，圆心为2(2,O ，半径为t ，∵曲线1C 与曲线2C 有两个不同交点，11,0t t t -<+>∴，11t <<，∴正数t的取值范围是1,1)． （10分） 考点：极坐标与普通方程的互化，参数方程与普通方程的互化．22．见详解【解析】试题分析：根据柯西不等式和不等式的基本性质证明． 试题解析：2222()()ax by ay bx ab a xy b xy abx aby ab ++-=+++-证明： 2222()(1)xy a b ab x y =+++-222()[()21]xy a b ab x y xy =+++--．（3分）1,x y +=∵ 22()()()2ax by ay bx ab xy a b abxy ++-=+-∴2()0xy a b =-≥(,0)x y >，()()ab ax by ay bx ∴++≤． （6分） 又22()()()()()()22ax by ay bx a x y b x y ax by ay bx ++++++⎡⎤⎡⎤++=⎢⎥⎢⎥⎣⎦⎣⎦≤ 22()24a b a b ++⎛⎫== ⎪⎝⎭. 2()()().4a b ab ax by ay bx +∴++≤≤ （10分） 考点：不等式证明。

云南省蒙自县文澜高级中学2013-2014学年高一上学期期末考试语文试题诗圣与文士性格的塑造宋代学者称杜甫为“圣手诗者”，这主要是指杜甫在诗歌史上的地位而言。

他们把杜甫视为“集大成”者，认为他是位无体不工、无美不备的诗人。

到了后世把杜甫简称为“诗圣”，这突出了诗的道德含义（郭沫若称其为“诗中圣哲”也是此意），符合杜诗中的儒学内涵。

“诗圣”的名号，使得杜甫所确立的“忧国忧民”思想逐渐成为了主流理论。

不管你是否赞成，但都不能不承认诗歌写作应该反映现实和关注国家与人民的命运。

南宋诗人就说“忧时本是诗人职，莫怪吟中感慨多。

”这是赞成诗人应该忧国忧民的。

也有不赞成的，明代的公安派代表作家袁宏道，提倡个性解放，不同意诗人应有“忧国忧民”的责任感。

他在《显灵宫集诸公以城市以林为韵》中说“新诗日日千余言，诗中无一忧民字”，“自从老杜得诗名，忧国忧民成儿戏”，仔细咀嚼诗意，可见袁宏道虽然不赞成此说，但还是把“忧国忧民”看作是当时诗歌创作中大多数诗人所遵循的原则。

这些都说明杜诗对后世士人影响之深。

诗歌创作乃是中国古代诗人日常功课之一，古代学子平常接触最多的当属杜诗。

因为杜诗规矩井然，学有规范。

如应酬中大量运用的律体诗，当以杜甫写得最好，很少率意之作。

科举考试中用的试帖诗可以模仿杜诗中的“五排”（杜甫以后，很少再有诗人写出像杜甫这样多的高质量的“五排”了）。

对杜诗的广泛模仿从宋代就开始了。

书商为了满足这个社会需求，还把杜诗分类编排，给模仿者以便利。

这样，杜诗中的思想感情必然会从阅读的渠道渗入到士人们的思想意识中去。

因此，说杜诗对后世文人士大夫性格的塑造产生影响绝不是夸诞之词。

中国的文学传统，特别是古典诗词对读者思想感情的陶冶力量是很难估量的。

杜甫诗发扬了儒家思想中富于伦理价值的思想，对古代读书人有很大影响；施之于今日的教育之中，也当有积极意义。

1．下列叙述中，不属于称杜甫“圣于诗者”或“诗圣”的根据的一项是A．杜甫在诗歌史上地位很高，人们视之为“集大成”者。

云南省蒙自县文澜高级中学2013-2014学年高一上学期期末考试数学试题1、已知集合{}{}1,0,1,B 11A x x =-=-≤<，则A ∩B ＝ A ．{}1,0,- B ． {}1,0,1- C ．{}1,1- D ．{}0,1 2. 已知函数x x f -=)(，则)(x f 是（ ） A ．奇函数 B ． 偶函数 C ．既是奇函数又是偶函数D ．非奇函数非偶函数3、函数2()2(1)421f x m x mx m =+++-的一个零点在原点，则m 的值为（ ） A ．0 B ．12 C ．-12D ．1 4、下列命题中正确的个数是（ ）①若直线l 上有无数个点不在平面α内，则l α∥．②若直线l 与平面α平行，则l 与平面α内的任意一条直线都平行．③如果两条平行直线中的一条与一个平面平行，那么另一条也与这个平面平行． ④若直线l 与平面α平行，则l 与平面α内的任意一条直线都没有公共点．A ．0Ｂ．1Ｃ．2Ｄ．35．函数()f x =） A ．[)()1,22,⋃+∞ B ．()1,+∞ C ．[)1,2 D ．[)1,+∞6．设1232,2()((2))log (1) 2.x e x f x f f x x -⎧⎪=⎨-≥⎪⎩＜，则的值为，（ ） A ．0 B ．1 C ．2 D ．3 7. 已知函数()(51)2f x a x =-+在R 上是增函数，则a 的取值范围是（ ）A ．),(+∞-∞B ．1,5⎛⎫-∞ ⎪⎝⎭C ．1,5⎛⎫+∞ ⎪⎝⎭D ．()5,+∞8．已知函数()f x 是定义在R 上的偶函数，当0x ≥时，()(1)f x x x =+，则当0x <时，()f x =( )A ．(1)x x +B ．(1)x x -+C ．(1)x x -D ．(1)x x --9．已知函数2()28f x x kx =--在[2,5]上是单调函数，则实数k 的取值范围是（ ）A ．8k ≤B ．20k ≥C ．820k k ≤≥或D ． 420k ≤≤10．函数y ＝a x －1a(a >0，且a ≠1)的图象可能是 ( )11、 如图是正方体的平面展开图，则在这个正方体中：①BM 与ED 平行． ②CN 与BE 是异面直线．③CN 与BM 成60˚角． ④DM 与BN 垂直．以上四个命题中，正确命题的序号是（ ） Ａ．①，②，③Ｂ．②，④ Ｃ．③，④Ｄ．②，③，④12、若函数()f x 、()g x 分别为R 上的奇函数、偶函数，且满足()()xf xg x e -=，则有 ( )A ．()()()230f f g <<B ．()()()032g f f <<C ．()()()203f g f <<D ．()()()023g f f <<第II 卷（非选择题 共90分）二、填空题：本大题共4分，每小题5分，共20分13、已知幂函数)(x f y =的图象过点=)9(),3,3(f 则14、用二分法求图象连续不断的函数)(x f 在区间(1,5)上的近似解，验证(1)(5)0,f f ⋅<给定精确度01.0=ε，取区间(1,5)的中点11532x +==，计算得1(1)()0f f x ⋅<，1()(5)0f x f ⋅>，则此时零点∈0x .（填区间）E15、如图，E 、F 分别为正方体的面11A ADD 、面11B BCC 的中心，则四边形E BFD 1在该正方体的面上的射影可能是___16．若函数y ＝f (x )为偶函数，且在(0，＋∞)上是减函数，又f (3)＝0，则()()02f x f x x+-<的解集为三、解答题：本大题共6小题，共70分，解答应写出文字说明、证明或演算步骤17计算题，每小题5分共10分 （1）--121445.00)2()49()53(e -++-； （2）211log 522lg 5lg 2lg502+++18（本小题12分）、若全集R U =，且{}15U C A x x x =<->或，{}93<<=x x B ，求：A ∩B ；A ∪B19（本小题12分）如图，在四棱锥P ABCD -中，底面ABCD 是矩形，PA ABCD ⊥平面，PA AB =，2BP BC ==，E ，F 分别是PB ，P C 的中点．(1)证明：EF ∥平面PAD；(2)求三棱锥E －ABC 的体积V ．20、（本小题满分12分）有甲乙两种产品，生产这两种产品所能获得的利润依次是P 和Q 万元，它们与投入资金x （万元）的关系为：432x P -=,)3(43+-=x Q ,今投入3万元资金生产甲、乙两种产品，为获得最大利润，对甲、乙两种产品的资金投入分别应为多少？最大利润是多少？21、（本题满分12分）已知312()2xx -≤，求函数y ＝(12)x 的值域22（本小题12分）()lg(2),()lg(2),()()().f x x g x x h x f x g x =+=-=+已知函数设（1）()h x 求函数的定义域。

2014届高三数学上册第一次月考文科试题（有答案）望江四中2014届高三上学期第一次月考数学（文）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答题时120分钟，满分150分。

第Ⅰ卷（选择题共10小题，每小题5分，共50分）一、选择题（每小题给出的四个选项中，只有一个选项符合题目要求．）1.若集合,,则（）A.B.C.D.答案：A解析：集合A＝{}，A＝{}，所以，2．设是虚数单位，则“x=－3”是“复数z=（x2+2x－3）+（x－1）i为纯虚数”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案：C【解析】若复数z=（x2+2x－3）+（x－1）i为纯虚数，则，所以“x=－3”是“复数z=（x2+2x－3）+（x－1）i为纯虚数”的充要条件。

3．已知为等差数列，若，则的值为（）A．B．C．D．答案：D解析：因为为等差数列，若，所以，，4.下列四个函数中,既是奇函数又在定义域上单调递增的是（）A．B．C．D．答案：C【解析】A、D既不是奇函数，也不是偶函数，排除，B只是在区间上递增，只以C符合。

5.已知函数有且仅有两个不同的零点，，则（）A．当时，，B．当时，，C．当时，，D．当时，，答案：B解析：函数求导，得：，得两个极值点：因为函数f（x）过定点（0，－2），有且仅有两个不同的零点，所以，可画出函数图象如下图：因此，可知，，只有B符合。

6.函数的最小正周期是（）A．B．C．2πD．4π答案：B【解析】函数,所以周期为.7.函数的零点所在的区间为（）A．B．C．D．答案：D【解析】＜0，＞0，所以，在上有零点。

8．设集合是的子集，如果点满足：，称为集合的聚点.则下列集合中以为聚点的有：；②；③；④（）A．①④B．②③C．①②D．①②④答案：A【解析】①中，集合中的元素是极限为1的数列，∴在的时候，存在满足0＜|x－1|＜a的x，∴1是集合的聚点②集合中的元素是极限为0的数列，最大值为2，即｜x－1｜≥1对于某个a＞1，不存在0＜|x－1|，∴1不是集合的聚点③对于某个a＜1，比如a=0.5，此时对任意的x∈Z，都有|x﹣1|=0或者|x﹣1|≥1，也就是说不可能0＜|x﹣1|＜0.5，从而1不是整数集Z的聚点④＞0，存在0＜|x－1|＜0.5的数x，从而1是整数集Z的聚点故选A9.一个盒子里有3个分别标有号码为1，2，3的小球，每次取出一个，记下它的标号后再放回盒子中，共取3次，则取得小球标号最大值是3的取法有（）A．12种B．15种C．17种D．19种答案：D解析：分三类：第一类，有一次取到3号球，共有取法；第二类，有两次取到3号球，共有取法；第三类，三次都取到3号球，共有1种取法；共有19种取法。

文澜高级中学2013届高三9月适应性考试（一）数学（文）试题第Ⅰ卷（选择题）一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，有且只有一项是符合题目要求的）一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，有且只有一项是符合题目要求的）1.设集合{}3,5,6,8A =,集合{}4,5,7,8B =,则A B I 等于（ ） A. {}3,4,5,6,7,8 B. {}3,6 C. {}4,7 D. {}5,82.设i 为虚数单位,若ab R b a bi a iiz 则),,(271∈+=-+=的值为（ ） A. 15- B. 3- C. 3 D. 153.若某商品销售量y (件)与销售价格x (元/件)负相关,则其回归方程可能是( ) A. 20010+-=x y B. 20010+=x y C. 20010--=x y D. 20010-=x y4.已知双曲线)0,0(12222>>=-b a by a x 的离心率为25,则椭圆)0(12222>>=+b a b y a x 的离心率为( ) A.21B. 33C. 23D. 225.已知点满足动点),(),4,5(y x P Q ⎪⎩⎪⎨⎧≥-≤-+≥+-,0102,022y y x y x ,则PQ 的最小值为( ) A. 5 B.34C. 2D. 76. 阅读右边的程序框图，运行相应的程序，当输入x 的值为25-时，输出的x 值为 （ ） A. 1- B. 1 C. 3 D. 97.一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为( ) A.π23B. π2C. π3D. π4 8.已知点P 在抛物线x y 42=上,那么点P 到点)1,2(-Q 的距离与点P 到抛物线的焦点的距离之和取得最小值时, 点P 的坐标为( )A. )1,41(-B. )1,41( C. )2,1( D. )2,1(-9.已知)(cos 3sin )(R x x x x f ∈+=,函数)(ϕ+=x f y 的图象关于直线0=x 对称,则ϕ的值可以是( )A.2π B.3πC.4π D. 6π10.等轴双曲线C 的中心在原点,焦点在x 轴上, C 与抛物线x y 162=的准线交于B A ,两点,34=AB ,则C 的实轴长为( )A. 2B. 22C. 4D. 811.已知球O 为棱长为1的正方体1111D C B A ABCD -的内切球,则平面1ACD 截球O 的截面面积为( ) A.π33 B. 3π C. π66 D. 6π 12. 已知数列}{n a 是首项为2,公差为1的等差数列,}{n b 是首项为1,公比为2的等比数列,则数列}{n b a 的前10项和等于( )A. 1033B. 1033-C. 2066D. 2066-第Ⅱ卷（非选择题）二、填空题: 本大题共4小题,每小题5分,共20分.三、解答题：解答应写出文字说明,证明过程或演算步骤. 17．（12分）设函数2sin 2)6sin()(2x x x f ++=π. (Ⅰ)求)(x f 的最小正周期;(Ⅱ)记b c a A f c b a C B A ABC 求若的对边分别为的内角,3,1,,1)(,,,,,===∆的值.18.(12分）已知函数75)1(2)(22-+++-=n n x n x x f 。

DC B A 云南省蒙自县文澜高级中学2013-2014学年高二上学期期中考试数学试题1、=∈===T S A n n x x T S 则已知集合},,|{},4,3,2,1{2( )}2,1{.}16,9{.}3,2{.}4,1{.D C B A2、的最大值为函数x y 2sin 1+= ( )0.3.2.1.D C B A3、==+462,8,}{a a a a n 则中在等差数列( )6.4.2.0.D C B A4、下列命题正确的是( )确定一个平面经过一条直线和一个点经过三点确定一个平面..B A 条直线确定一个平面两两相交且不共点的三四边形确定一个平面..D C5、得到的几何体锥将长方体截去一个四棱,则该几何体的左视图为如图所示,( )6、轴对称的直线方程是关于直线x x y 1+-= ( )1.1.1.1.--=-=+-=+=x y D x y C x y B x y A7、的定义域为函数x x x y +-=)1(( )}1|{.}0|{.≥≥x x B x x A }10|{.}0{}1|{.≤≤≥x x D x x C1π8、的图象可能是与函数时，在同一坐标系中，当x y a y a a x log 10==<<-( )9、的值为则已知ααα44cos sin ,55sin -=( ) 53.51.53.51.D C B A --10、项和为的前则数列若列是公比为正数的等比数设7}{,16,1,}{51n n a a a a ==( )128.127.64.63.D C B A11、H G F E D C B A ABCD 、、、中，如图，在正方体1111-EF C B BB AB AA 的中点，则异面直线、、、分别是1111所成的角等于与GH ( )︒︒︒︒120.90.60.45.D C B A12、则球的体积为所得的截面面积为的平面去截球用与球心距离为,,1π ( )332.28.328.38.ππππD C B A 第Ⅱ卷 (非选择题，共90分)二、填空题： (本大题共四小题，每小题5分，共20分)13、的最小值为函数)0(1)(>+=x xx x f ．14、垂直，与直线直线02012=++=+-y ax y x 等于则a ． 15、,1)1(,5)(=f R x f 且满足的奇函数上周期为是若=-=)4()3(,2)2(f f f 则．16、)2||,0)(tan()(πϕωϕω<>+=x A x f 已知函数=)24(,πf 则的部分图象如图 ．三、解答题：（本题共6小题，共70分。

2014届高三数学文科高考模拟试卷考生须知：1、全卷分试卷I 、II ，试卷共4页，有三大题，满分150分。

考试时间120分钟。

2、本卷答案必须做在答卷I 、II 的相应位置上，做在试卷上无效。

3、请用蓝、黑墨水笔或圆珠笔将姓名、准考证号分别填写在答卷I 、II 的相应位置上，用2B 铅笔将答卷I 的准考证号和学科名称所对应的方框内涂黑。

参考公式：如果事件A , B 互斥, 那么 棱柱的体积公式P (A +B )=P (A )+P (B )V =Sh如果事件A , B 相互独立, 那么 其中S 表示棱柱的底面积, h 表示棱柱的高 P (A ·B )=P (A )·P (B )棱锥的体积公式如果事件A 在一次试验中发生的概率是p , 那么n V =31Sh次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示棱锥的底面积, h 表示棱锥的高 P n (k )=C kn p k (1－p )n -k (k = 0,1,2,…, n ) 球的表面积公式棱台的体积公式S = 4πR 2)2211(31S S S S h V ++=球的体积公式其中S 1, S 2分别表示棱台的上.下底面积, h 表示棱台 V =34πR 3的高 其中R 表示球的半径选择题部分(共50分)一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.如图，全集}9,7,6,4,2,1{=I , 其中}9,7,4,2{=M ，}9,7,4,1{=P ,}7,4,2{=S 是I 的3个子集，则阴影部分所表示的集合等于 （ ▲ ）（A ）}9,7,4{ （B ）}9,7{ （C ）}9,4{ （D ）}9{2.已知a R ∈，则“2a >”是“22a a >”成立的（ ▲ ）（A ）充分不必要条件 （B ）必要不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件3.已知βα,是不同的两个平面，n m ,是不同的两条直线，则下列命题中不正确．．．的是（ ▲ ） （A ）若α⊥m n m ,//，则α⊥n （B ）若,m m αβ⊥⊥，则αβ∥ （C ）若βα⊂⊥m m ,，则αβ⊥ （D ）若,m n ααβ= ∥，则m n ∥4.下列函数中，既是偶函数又在) , 0(∞+上单调递增的是（ ▲ ）（A ）||ln x y = （B ）2x y -= （C ）xe y = （D ）x y cos = 5. 某中学高三理科班从甲、乙两个班各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如右图，其中甲班学生成绩的平均分是85，乙班学生成绩的中位数是83，则x +y 的值为（ ▲ ）（A ）8 （B ）7 （C ）9 （D ）168（第5题）乙甲y x 6119261180567986. 函数)(x f y =的图象向右平移3π单位后与函数x y 2sin =的图象重合，则)(x f y =的解析式是（ ▲ ） （A ）()f x =)32cos(π-x （B ）()f x =)62cos(π-x （C ）()fx =)62cos(π+x （D ）()f x =)32cos(π+x7.已知函数n mx x x f 231)(23+-=（n m ,为常数），当2=x 时，函数)(x f 有极值，若函数)(x f 只有三个零点，则实数n 的取值范围是（ ▲ ）（A ）]35,0( （B ）)32,0( （C ）)35,1[ （D ）]32,0[ 8.已知向量OA ,OB 的夹角为60°，|OA |=|OB |=2，若OC =2OA +OB，则△ABC 为 （ ▲ ）（A ）直角三角形 （B ）等腰三角形 （C ）等边三角形 （D ）等腰直角三角形9.P 为双曲线221916x y -=右支上一点，12,F F 分别是双曲线的左焦点和右焦点，过P 点作 12PH F F ⊥，若12PF PF ⊥，则PH = （ ▲ ）（A ）645 （B ）85 （C ）325 （D ）16510.已知函数⎪⎩⎪⎨⎧≥-<-=2,132|,12|)(x x x x f x ，若方程0)(=-a x f 有两个不同的实数根，则实数a的取值范围为 （ ▲ ） （A ）)3,1( （B ）)3,1[（C ）)1,0( （D ）)3,0(非选择题部分(共100分)二、填空题: 本大题共7小题, 每小题4分, 共28分。

云南省蒙自县文澜高级中学2014届高三10月月考理综试题1、在某细胞培养液中加入32P标记的磷酸分子，短时间内分离出细胞的ATP，发现其含量变化不大，但部分ATP的末端磷酸基团已带上放射性标记，该现象能够说明的是( )①ATP中远离腺苷的磷酸基团容易脱离②32P标记的ATP是新合成的③ATP是细胞内的直接能物质④该过程中ATP既有合成又有分解A．①②③④ B．①②④ C．①②③ D．②③④2．一种观赏鱼能忍受缺氧，在4℃下缺氧l2小时后，组织中乳酸与乙醇浓度如下表，其中乙醇是乳酸在厌氧代谢中形成的。

结合表格可知，这种观赏鱼在缺氧A．组织中的乳酸与平时相差不多 B．形成乙醇可使观赏鱼鱼避免酸中毒C．厌氧代谢终产物为乳酸 D．生命活动的能量自有氧呼吸3、下图为探究酵母菌进行的呼吸作用类型的装置图，下列现象中能说明酵母菌既进行有氧呼吸，同时又进行无氧呼吸的是( )A．装置1中液滴左移，装置2中液滴不移动B．装置1中液滴不动，装置2中液滴右移C．装置1中液滴左移，装置2中液滴右移D．装置1中液滴右移，装置2中液滴左移4、关于叶绿体色素的叙述，错误的是（）A.提取光合色素，进行纸层析分离时，胡萝卜素位于滤纸最上方，原因是其在提取液中的溶解度最大B.叶绿素a和叶绿素b都含有镁元素C.叶绿素a和叶绿素b在红光区的吸收峰值不同D.植物呈现绿色是由于叶绿素能有效地吸收绿光5、将一植物放在密闭的玻璃罩内，置于室外进行培养。

假定玻璃罩内植物的生理状态与自然环境中相同，用CO2测定仪测得了一天内该玻璃罩内CO2浓度变化情况，绘制成下图所示的曲线（水平虚线：实验开始时玻璃罩内CO2浓度），下列有关说法正确的是( )A．BC段较AB段CO2增加减慢，是因低温使植物呼吸作用减弱B．CO2下降从D点开始，说明植物进行光合作用是从D开始的C．FG段CO2下降不明显，是因为光照减弱，光合作用减弱D．H点CO2浓度最底，说明此时植物对CO2的吸收最多，光合作用最强6、下图为小鼠结肠癌发病过程中细胞形态和部分染色体上基因的变化。

新课标2014届高三第一次月考数学文科考试试题一、选择题（每小题5分，共60分）1、设集合2{|20,}S x x x x R =+=∈, 2{|20,}T x x x x R =-=∈,则S T = （ ）A ．{0}B ． {0,2}C ．{2,0}-D ．{2,0,2}-2、命题“存在04,2<-+∈a ax x R x 使为假命题”是命题“016≤≤-a ”的（ ）A ．充要条件B ．必要不充分条件C ．充分不必要条件D ．既不充分也不必要条件 3、设5.05.05232.0,log ,log -===c b a 则（ ）A ．b c a <<B ． a c b <<C ． c b a <<D ．c a b <<4、函数(2),2()2,2x f x x f x x -+<⎧=⎨≥⎩ ，则)5(-f 的值为（ ）A ．2B ．8C ．18D ．125、曲线x x y ln 42+=在点A(1,1)处的切线的斜率是( )A ．4B ．5C ．6D ．76、若函数)(x f y =的值域是[1,3]，则函数)3(21)(+-=x f x F 的值域是（ ）A 、 [-5,-1]B 、 [-2,0]C 、 [-6,-2]D 、 [1,3]7．已知a>0,b>0,且1ab =,则函数()x f x a = 与函数()1b g x og x =的图象可能是( )8、函数)(x f 的导函数为)(x f '，且满足)2(23)(2f x x x f '+=，则)5(f '的值为（ ）A ．5B ． 1C ． 6D ． -29．已知函数()f x 是R 上的奇函数,对于(0)x ∀∈+∞，，都有(2)()f x f x +=-，且(]01x ∈，时,()21x f x =+，则)2014()2013(f f +的值为（ ）学校 班级_____ __ 姓名________ ____ 学号____ ___ …………………………………… 密 ……………………… 封 …………………… 线……………………………………A ．1B ．2C ．3D ．410．函数xx x f 214)(-=的图象（ ）（A ） 关于原点对称 （B ） 关于直线y ＝x 对称 （C ） 关于x 轴对称 （D ） 关于y 轴对称 11．若函数()21=f x x ax x ++在1,+2⎛⎫∞ ⎪⎝⎭是增函数,则a 的取值范围是( ) (A)[-1,0] (B)[1,)-+∞ (C)[0,3] (D)[3,)+∞12．设f(x)，g(x)分别是定义在R 上的奇函数和偶函数，当x <0时，0)(')()()('<+x g x f x g x f ，且0)3(=-f ，则不等式0)()(<x g x f 的解集是( ） A ．(－3，0)∪(3，+∞) B ．(－3，0)∪(0，3) C ．(－∞，－3)∪(3，+∞)D ．(－∞，－3)∪(0，3)二、填空题（每题5分，共20分）13、函数)2(log 221x x y -=的单调递减区间是____________．14．函数f(x)=cosx -log 8x 的零点个数为_____________.15、点P 是曲线x x y ln 2-=上任意一点, 则点P 到直线2+=x y 的距离的最小值是 ___. 16．下列命题:①若函数)lg()(2a x x x f ++=为奇函数,则a =1; ②函数|sin |)(x x f =的周期；π=T ③方程x x sin lg =有且只有三个实数根; ④对于函数x x f =)(,若210x x <<,则2)()()2(2121x f x f x x f +<+. 以上命题为真命题的是 ______________.(写出所有真命题的序号)新课标2014届高三第一次月考数学文科考试试题一、选择题（满分60分,每小题5分）题号1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题（满分20分,每小题5分）13、 14、 15、 16、 三、解析题（共70分）17．(12分)已知集合{}.1521,052+<<+=⎭⎬⎫⎩⎨⎧<-+=a x a x P x x x S（1） 求集合S（2） 若P S ⊆，求实数a 的取值范围．18、已知函数)(x f 对于一切R y x ∈、，都有，)()()(y f x f y x f +=+且)(x f 在R 上为减函数，当0>x 时，0)(<x f ，2)1(-=f 。

云南省蒙自县文澜高级中学2014届高三10月月考数学（理）试题1．设全集{}1,2,3,4,5U =,{}0232≤+-∈=x x Z x A ,{}2,3,4B =则=⋃B A C U )(A ．{}3,4B ．{}3,4,5C ．{}2,3,4,5D ．{}1,2,3,42. 设复数Z 满足i Z i 21)1(+=+，则在复平面内，Z 的共轭复数的点位于 A.第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3等差数列{}n a 的前n 项和为n S ，已知58a =，3=6S ，则9=a A ．8 B ．12 C ．16 D ．24． 4. 下列命题中是假命题的是①过平面外一点有且只有一条直线与该平面垂直； ②过平面外一点有且只有一条直线与该平面平行； ③如果两个平行平面和第三个平面相交，那么所得的两条交线平行； A ．① B ．② C ．③ D ．④ 5. 已知（1+ax ）(1+x)5的展开式中x 2的系数为-5，则a= A.-4B.-3C.-2D.-16. 若曲线2y x ax b =++在点(0,)b 处的切线方程是10x y -+=，则A.1,1a b ==B. 1,1a b =-=C. 1,1a b ==-D. 1,1a b =-=- 7. 若1tan 4,tan θθ+=则sin 2θ= A ． 15 B ． 13 C ． 23 D ． 128. 执行右边的程序框图所得的结果是A ．3 B. 4 C. 5 D. 69. 已知a ＞0，x ，y 满足约束条件()133x x y y a x ⎧≥⎪+≤⎨⎪≥-⎩ ,若z=2x+y 的最小值为23，则a=A. 14B. 12C.1D.210. 已知log 2a ＋log 2b ≥1，则3a ＋9b 的最小值为A ．6B ．9C ．16D ．1811.下列关于函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭的结论，其中正确结论是①图象关于原点成中心对称；②图象关于直线12x π=成轴对称；③图象可由函数2sin 2y x =的图象向左平移3π个单位得到；④图象向左平移12π个单位，即得到函数2cos 2y x =的图象。