五年级数学培优之速算与巧算
- 格式:doc
- 大小:57.50 KB
- 文档页数:9

五年级上册数学培优专题--快速计算1. 引言数学是一个重要的学科,对培养学生的思维能力和解决问题的能力至关重要。
快速计算是数学研究的基础,也是提高学生计算效率和准确性的关键。
本文档将介绍五年级上册数学培优专题中的快速计算方法和技巧。
2. 快速加法- 单位位上的加法:学生可以通过掌握单个数字的加法运算,快速进行十位以内的加法计算。
- 进位加法:学生应掌握进位加法的方法,在进行大数相加时能快速判断和进行进位操作。
- 快速近似相加法:学生可以通过近似相加法,将加法问题简化,快速估算结果。
3. 快速减法- 单位位上的减法:学生应通过掌握单个数字的减法运算,快速进行十位以内的减法计算。
- 不退位减法:学生应掌握不退位减法的方法,在进行大数相减时能够快速判断和进行减法操作。
- 快速近似相减法:学生可以通过近似相减法,将减法问题简化,快速估算结果。
4. 快速乘法- 乘法口诀表:学生应掌握乘法口诀表,通过熟记口诀表的内容,进行快速乘法计算。
- 快速近似相乘法:学生可以通过近似相乘法,将乘法问题简化,快速估算结果。
- 分解法:学生可以通过分解法,将大数乘法问题分解为小数乘法问题,进行快速计算。
5. 快速除法- 除法口诀表:学生应掌握除法口诀表,通过熟记口诀表的内容,进行快速除法计算。
- 快速近似相除法:学生可以通过近似相除法,将除法问题简化,快速估算结果。
- 除法分配率:学生应掌握除法和乘法之间的分配率,能够灵活运用进行快速计算。
6. 实际应用快速计算在日常生活中有着广泛的应用。
学生可以通过进行日常生活中的计算练,提高计算效率和准确性。
同时,学生也可以通过数学游戏、竞赛等方式进行快速计算的训练,激发兴趣,提高研究效果。
7. 结论通过研究和掌握快速计算的方法和技巧,学生可以提高计算效率和准确性,为进一步研究数学奠定坚实的基础。
快速计算是培优专题中重要的一环,帮助学生更好地掌握数学知识,提高数学研究的兴趣和能力。
以上是五年级上册数学培优专题--快速计算的文档内容。


五年级数学巧算技巧巧算是一种数学技巧,可以帮助我们更快速、更准确地计算。
对于五年级的学生来说,掌握一些基本的巧算技巧是非常有用的。
以下是一些五年级数学巧算技巧:1. 乘法分配律:a×(b+c)=a×b+a×c这个公式可以帮助我们将一个复杂的乘法问题分解成两个或更多简单的乘法问题。
例如,计算101×35 时,我们可以将其拆分为(100+1)×35,这样就可以利用乘法分配律进行计算了。
2. 提取公因数:将两个数的乘积提取出公因数,简化计算。
例如,计算25×48 时,我们可以将其拆分为25×(40+8),然后提取公因数 25,得到25×40+25×8。
3. 乘法结合律:(a×b)×c=a×(b×c)这个公式可以帮助我们在计算大数相乘时,将大数分解成两个或更多小数的乘积,然后利用结合律进行计算,减少进位的次数。
例如,计算9999×8 时,我们可以将其拆分为×8,然后利用结合律进行计算。
4. 除法的性质:(a/b)÷(c/d)=(a/b)×(d/c)这个公式可以帮助我们在计算除法时,将除法转化为乘法,简化计算。
例如,计算72÷(3/4) 时,我们可以将其转化为72×(4/3),这样就可以直接计算出结果了。
5. 分数加减法:分母相同、分子直接相加减;分母不同、通分后再加减。
这个技巧可以帮助我们在进行分数加减法时,快速找到分母相同的分数,或者将分母不同的分数通分后再进行加减。
例如,计算 (1/2)+(3/4) 时,我们可以将其转化为 (2/4)+(3/4),然后直接计算出结果。
以上是一些五年级数学巧算技巧,希望对你有所帮助。

以下是五年级数学速算方法与技巧:
1.记忆乘法口诀表,尤其是基础的1-10乘法口诀。
2.利用数学规律,例如将一个数乘以10,就是在这个数的末尾加上
一个0。
3.拆分法,即将一个大的数拆分成两个较小的数相乘。
例如,计算
38×25,可以拆分成(30+8)×25=750+200=950。
4.快速除法,即利用除数的因数分解和被除数的规律进行简化计算。
例如,计算28÷4,可以将4分解成2×2,然后将28分别除以2得到14,再将14除以2得到7,因此28÷4=7。
5.利用分数的关系进行运算,例如计算1/4+1/3,可以先找到它们的
公共分母为12,然后将分子加起来得到7/12。
6.利用角度的关系进行计算,例如计算120°+150°,可以将150°
减去120°得到30°。
7.利用化简方法进行计算,例如计算(3+4)×(5+2),可以先用括号里
面的数计算得到7×7=49。
8.利用逆运算进行计算,例如计算63-28,可以先用逆运算28+?=63
得到35,再将35作为答案。
以上是五年级数学速算方法与技巧,希望对同学们有所帮助。

小学五年级奥数题——速算与巧算在日常生活和解答数学问题时,经常要进行计算,在数学课里我们学习了一些简便计算的方法,但如果善于观察、勤于思考,计算中还能找到更多的巧妙的计算方法,不仅使你能算得好、算得快,还可以让你变得聪明和机敏。
例1:计算:9.996+29.98+169.9+3999.5解:算式中的加法看来无法用数学课中学过的简算方法计算,但是,这几个数每个数只要增加一点,就成为某个整十、整百或整千数,把这几个数“凑整”以后,就容易计算了。
当然要记住,“凑整”时增加了多少要减回去。
9.996+29.98+169.9+3999.5=10+30+170+4000-(0.004+0.02+0.1+0.5)=4210-0.624=4209.376例2:计算:1+0.99-0.98-0.97+0.96+0.95-0.94-0.93+…+0.04+0.03-0.02-0.01解:式子的数是从1开始,依次减少0.01,直到最后一个数是0.01,因此,式中共有100个数而式子中的运算都是两个数相加接着减两个数,再加两个数,再减两个数……这样的顺序排列的。
由于数的排列、运算的排列都很有规律,按照规律可以考虑每4个数为一组添上括号,每组数的运算结果是否也有一定的规律?可以看到把每组数中第1个数减第3个数,第2个数减第4个数,各得0.02,合起来是0.04,那么,每组数(即每个括号)运算的结果都是0.04,整个算式100个数正好分成25组,它的结果就是25个0.04的和。
1+0.99-0.98-0.97+0.96+0.95-0.94-0.93+…+0.04+0.03-0.02-0.01=(1+0.99-0.98-0.97)+(0.96+0.95-0.94-0.93)+…+(0.04+0.03-0.02-0.01)=0.04×25=1如果能够灵活地运用数的交换的规律,也可以按下面的方法分组添上括号计算:1+0.99-0.98-0.97+0.96+0.95-0.94-0.93+…+0.04+0.03-0.02-0.01=1+(0.99-0.98-0.97+0.96)+(0.95-0.94-0.93+0.92)+…+(0.03-0.02-0.01)=1例3:计算:0.1+0.2+0.3+…+0.8+0.9+0.10+0.11+0.12+…+0.19+0.20 解:这个算式的数的排列像一个等差数列,但仔细观察,它实际上由两个等差数列组成,0.1+0.2+0.3+…+0.8+0.9是第一个等差数列,后面每一个数都比前一个数多0.1,而0.10+0.11+0.12+…+0.19+0.20是第二个等差数列,后面每一个数都比前一个数多0.01,所以,应分为两段按等差数列求和的方法来计算。

五年级上册数学培优专题--迅捷计算
一、引言
数学作为一门基础学科,对学生的思维能力和逻辑思维能力有
着重要的培养作用。
为了帮助五年级学生提高计算速度和思维敏捷度,本文将介绍一些迅捷计算的方法和技巧。
二、加法技巧
1. 近似相加法:当计算两个大数相加时,可以先去掉最高位的零,然后将其他位数相加再加上最高位的零。
2. 逢九进一法:当计算两个数相加时,如果个位数相加等于9,则十位数进一。
3. 运用补数法:当计算的两个数中,一个数减去一个比较接近
的数的差加上这个较小的数等于第二个数时,可以利用这个关系进
行计算。
三、减法技巧
1. 借位法:当减法的某一位无法相减时,可以从前一位借位。
2. 运用差补法:当计算两个接近的数相减时,可以先计算其相
反数,再将相反数的差的相反数作为补数,与第二个数相加。
四、乘法技巧
1. 运用倍数法:当计算一个数与10的倍数相乘时,可以将这个数后面加上相应的零。
2. 分解相乘法:将一个数拆解为两个能够相乘的数,然后进行相乘计算。
五、除法技巧
1. 运用倍数法:将要除的数和被除的数与10的倍数对齐,然后进行除法计算。
2. 取整法:将被除数最高位对齐后进行整数除法计算,得到商后再将商与余数相加,得到最终结果。
六、结语
通过掌握这些迅捷计算的方法和技巧,五年级的学生可以更加高效地进行数学计算,提高计算速度和思维敏捷度。
希望学生们能够在研究数学的过程中积极运用这些技巧,并取得更好的成绩。
以上是五年级上册数学培优专题--迅捷计算的简要介绍。
如果您对这个话题需要更加详细的探讨,可以进一步讨论。

【同步教育信息】本周教学内容:速算与巧算(一)同学们,今天我们一起来研究速算与巧算,在数的运算中根据数的特点及数与数之间的特殊关系,恰当地利用四则运算中的规律,不但可以提高运算速度,而且还能使我们的计算又准又快,锻炼思维,提高运算的技能技巧。
[学习过程]一. 阅读思考:例1. 简算:(1)9968068⨯+...分析:题中,9.9接近10,且6.8和0.68都是有6、8这两个数字。
解法一:解法二:或9968068⨯+...(2)288125280125..⨯-⨯分析:审题可知,125和12.5可以互相转化解:288125280125⨯-⨯..或288125280125⨯-⨯..例2. 计算7685614÷⨯...分析:这道题是乘除同级运算,解答时,利用添括号法则,在“÷”后面添括号,括号里面要变号,“×”变“÷”,“÷”变“×”。
不过,同学们请注意,这种方法只适用于乘、除同级运算。
解:7685614÷⨯...例3. ()+÷77728077分析:我们可以把乘法分配律引申开,用来解题。
解:()+÷77728077二. 尝试体验1. 请你判断下面的做法是否简便、正确。
(1)84487948..⨯-⨯(2)84487948..⨯-⨯2. 先按提示要求完成下面题的计算,再比较哪种算法巧,说说巧算的依据。
(1)()-÷130052013(2)()-÷130052013【模拟试题】(答题时间:20分钟)1. 53125043125⨯-⨯...2. 0616684⨯+⨯..3. 14415613..÷⨯4. 6355711⨯÷÷5. ()()⨯⨯÷⨯⨯4875812425276. 343535353434⨯-⨯【试题答案】1. 53125043125⨯-⨯...12.52. 0616684⨯+⨯..603. 14415613..÷⨯124. 6355711⨯÷÷455. ()()487581242527⨯⨯÷⨯⨯186. 343535353434⨯-⨯【励志故事】茄子的好坏富翁对仆人说:“茄子增进食欲,是好东西。

第二讲小数的速算与巧算(二)【知识概述】若干个数排成一列称为“数列”,数列中的每一个数称为一项,其中第一项称为首项(a1 ),最后一项称为末项(a n )。
从第二项开始,后项与前项之差都相等的数列称为“等差数列”,后项与前项之差称为公差( d ),数列中的数的个数称为项数(n )。
对于等差数列,我们要熟练运用三个公式:通项公式:第门项=首项+(项数—1)X公差项数公式:项数=(末项—首项)十公差+ 1求和公式:和=(首项+末项)X项数十21 、对于一个数除以两个或者两个以上的数,我们可以把多个除数先用乘积的方式算出结果,再用被除数除以所求的结果,得到最后的商例 1 计算8.376 - 3.2 - 2.5解析:8.376除以3.2再除以 2.5 也就是8.376除以3.2 与2.5 的乘积练习计算7.68 -2.5 P.42、一个数除以另一个数就等于这个数乘以这个数的倒数,即a*b=a X1/b=a/b例2 计算(4.8 X 7.5 X 8.1 ) -( 2.4 X 2.5 X 2.7 )解析:因为乘除是同一级运算,我们可以把式子拆开,看作是( 4.8-2.4)X (7.5-2.5)X (8.1 -2.7)练习 1.1 -( 1.1 - 1.2 ) -( 1.2 - 1.3 ) -( 1.3 - 1.4 )3.数列通项公式:第门项=首项+(项数—1)X公差, 项数公式:项数=(末项—首项)十公差+ 1,求和公式:和=(首项+末项)X项数十2等差数列就是一列数,后面的数减去前面的数所得的差都是相等的例3已知等差数列0.2 , 0.5 , 0.8 , 1.1 , 1.4,…。
(1) 这个数列的第1 3项是多少?( 2) 4.7 是其中的第几项?解析:第13项等于首项+ (n-1 ) X公差=0.2+ (13-1 )X 0.3,4 .7= 0.2+(n-1 ) X0.3, 求得的n 就是第几项练习:有一列数0.1 ,0.5,0.9,1.3,1.7,( 1 ) 它的第1000 项数是多少?( 2) 492.1 是它的第几项?一只小虫沿着笔直的树干往上跳。

五年级数学速算方法数学速算是指通过加减乘除的运算法则,以及一些巧妙的计算技巧,以最快的速度解答数学题目。
下面将介绍一些适用于五年级学生的数学速算方法。
一、加法速算法则1.同进同退法:对于两个数相加,可以通过“同进同退”来加快计算速度。
例如:56 + 26实际可以计算成50 + 20 + 6 + 6,先将个位数同进同退计算,再计算十位数同进同退。
2.进位法则:当相加的两个数相加大于10时,在个位数上保留余数,将十位数向前进位。
例如:37 + 25实际可以计算成30 + 20 + 7 + 5,进位后为32 + 10 = 42。
3.估计法则:对于两个数相加,可以通过估计其大小来快速计算。
例如:78 + 44实际可以计算成80 + 40 + 2 + 4,先估计后计算。
二、减法速算法则1.差的倍数法:对于减法运算,可以通过找出差的倍数来加快计算速度。
例如:94 - 28可以通过找出差的倍数,如70,再计算14,得到66。
2.进退法则:当减法运算中的个位数相减小于0时,在十位数上向前退位,个位数加10。
例如:863 - 215可以计算成853 - 205,然后得到648。
3.退位法则:当减法运算中的个位数大于被减数的个位数时,在个位数上向前退位,十位数减去1。
例如:986 - 529可以计算成975 - 519,然后得到456。
三、乘法速算方法1.单位数相乘法:当计算两个单位数相乘时,可以直接将两个数相乘得到结果。
例如:7 × 9 = 63。
2.十位数相乘法:当计算十位数与个位数相乘时,可以将十位数与个位数分别与被乘数相乘,再求和得到结果。
例如:24 × 3 = 20 × 3 + 4 × 3 = 60 + 12 = 72。
3.整十整百相乘法:当计算整十数或整百数与个位数相乘时,将个位数与十位数直接相乘得到结果,并在末尾添加0。
例如:30 × 4 = 120。

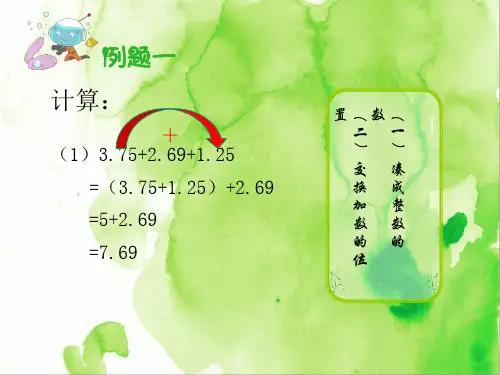
1 第一讲 速算与巧算 知识要点与学法指导: 1. 利用定律、性质进行速算,提高计算能力。
2. 引导学生发现数据特征,运用运算定律进行简单巧算。 3.让学生会运用“凑整”、“分拆”的方法进行简便运算。 4. 加、减法的一些运算性质: (1)a+(b+c)=a+b+c (2)a+(b-c)=a+b-c (3)a-(b+c)=a-b-c (4)a-(b-c)=a-b+c
例1 巧算下列各题:
(1)219+648+51-138-548-62 (2)100+99-98-97+96+95-94-93+……+8+7-6-5+4+3-2-1 【分析与解】 观察这个算式,可以发现219和51相加凑整,648和548相减
凑整,再利用减法性质a-b-c=a-(b+c),使138+62也凑整。 2
所以: 解:(1)原式=(219+51)+(648-548)-(138+62) =270+100-200 =170 这道题是100以内自然数的加减,共有100个数进行加减,直接计算显然太烦琐,题目中的运算符号,是按两加两减的规律排列的,可按每两个数一组进行分组,正好所得的差都是2。所以: 解:(2)原式=(100-98)+(99-97)+(96-94) +(95-93)+……+(8-6)+(7-5) +(4-2)+(3-1) =2×50 =100 如果从第二个数开始每连续的4个数为一组,可以分为: 100+(99-98-97+96)+(95-94-93+92)+……+(3-2-1)。你会计算吗? 想一想:还有没有其他的巧解方法?(从第一个数开始,每相邻的4个数为一组) 试一试1 (1)198+394-94+2+81 (2)100-99+98-97+96-95+……+4-3+2-1
例2 巧算下列各题。
(1)348-179 (2)2356-(256+159) 【分析与解】 可以先把179分拆,拆成有一个和被减数尾数相同的数,再进行计算。 解:(1)原式=348-148-31 =200-31 =169 【分析与解】 3
可以把括号内的数凑成和被减数尾数相同的数,再利用减法性质:a-(b+c)=a-b-c使运算简便。 解:(2)原式=2356-(256+100+59) =2356-356-59 =2000-59 =1941 试一试2 (1)938-589 (2)4636-(436+281)
以上两题运用的是“凑整”和“拆分”的方法,使运算简便。 例3 计算:599996+49997+3998+407+89
【分析与解】 观察这道题目,每个加数它们都是接近整十万、整万、整千……的数,可以先把它们转化为整十、整百的数减去一个数的形式,再把整十、整百的数和减去的那个数分别计算。 解:原式=(600000-4)+(50000-3)+(4000-2)+ (400+7)+(90-1) =654490-4-3-2+7-1 =654487 试一试3 98+998+9998 乘法运算中可以运用交换律、结合律和分配律,使运算简便。 即:乘法交换律:a×b=b×a; 乘法结合律:a×b×c =(a×b)×c =a×(b×c); 乘法分配律:(a±b)×c=a×c± b×c
例4 巧算下列各题:
(1)18×4×25 (3)125×(10+8) 4
(2)125×(16×8) (4)(20-4)×25 【分析与解】 利用乘法结合律,先算4×25,再算18×100。(2)题也是这样的特点。 解:(1)原式=18×(4×25) =18×100 =1800 解:(2)原式=(125×8)×16 =1000×16 =16000 【分析与解】 (3)、(4)题都是直接运用乘法分配律进行计算的,乘法对加法的分配律,也适用于减法。 解:(3)原式=125×10+125×8 =1250+1000 =2250 (4)原式=20×25-4×25 =500-100 =400 有些题目可以将乘法分配律反过来使用,即 a×b±a×c=a×(b±c)。 这个公式极为常用,一定要掌握。 试一试4 (1)125×72 (2)153×25+25×47 (3)67×54+67×45+67
例5 巧算下列各题:
(1)17×21 (2)11111×99999 (3)275÷25 5
【分析与解】 (1)题把21转化成20+1,就也可以运用乘法分配律计算了。而(2)中的99999可以写成10000-1的形式,再运用乘法分配律进行计算。 解:(1)原式=17×(20+1) =340+17 =357 解法一 解:(2)原式=11111×(100000-1) =1111100000-11111 =1111088889 这里再介绍一种一个数乘11、111、1111……的简便算法,11、111、1111……可以表示为10+1, 100+10+1, 1000+100+10+1……的形式,再运用乘法分配律进行计算,可以使计算简便。所以: 解法二:原式=99999×(10000+1000+100+10+1) =999990000+99999000+9999900 +999990+9999 =1111088889 【分析与解】 (3)从题目中可以看出,除数如果扩大4倍,变成100,可以使运算简便;根据商不变性质,“被除数和除数同时乘或除以相同的非零数,商不变,”把被除数和除数同时乘4,所以: 解:(3)原式=(275×4)÷(25×4) =1100÷100 =11 试一试5 (1)25×24 (2)9999×2222 (3)132476×111 (4)1375÷125 6
例6 巧算下列各题。
(1)260×(740÷260) (2)390÷(390÷220) (3)5250÷125÷8 (4)532÷(19×14) (5)(121×52×15)÷121 (6)(39+65+13)÷13 (7)46÷7-11÷7 【分析与解】 (1)一个数乘两个数的商,可以用这个数先乘商里的被除数,再除以商里的除数。也可以先用这个数除以商里的除数,再乘商里的被除数。用字母表示为:a×(b÷c)=a×b÷c =a÷c×b。 260×(740÷260) =260÷260×740 =1×740 =740 (2)一个数除以两个数的商,可以用这个数先除以商里的被除数,再乘商里的除数。用字母表示为:a÷(b÷c)=a÷b×c。 390÷(390÷220) =390÷390×220 =1×220 =220 (3)、(4)在连除式中,一个数除以另一个数所得商,再除以 第三个数,等于第一个数除以第二、三两个数的积,反之也成立。 用字母表示为:a÷b÷c=a÷(b×c)。 5250÷125÷8 532÷(19×14) =5250÷(125×8) =532÷19÷14 =5250÷1000 =28÷14 =5.25 =2 (5)几个因数的积除以一个数,可以用其中一个因数除以这个数后,再和其它的因数相乘。 用字母表示为:(a×b×c)÷d=a÷d×b×c 7
=b÷d×a×c =c÷d×a×b (121×52×15)÷121 =121÷121×52×15 =1×52×15 =780 (6)几个数的和除以一个数,可以把各个加数分别除以这个数,再把所得的商相加。 用字母表示为:(a+b+c)÷d=a÷d+b÷d+c÷d (39+65+13)÷13 =39÷13+65÷13+13÷13 =3+5+1 =9
(7)两个数的差除以一个数,可以把被减数和减数分别除以这个数,再把所得的商相减。用字母表示为:(a-b)÷c=a÷c-b÷c 46÷7-11÷7 =(46-11)÷7 =35÷7 =5 试一试6 (1)36×(66÷36) (2)280÷(280÷86) (3)266÷(7×38) (4)3250÷250÷4 (5)(25×26×15)÷25 (6)(360+24+60)÷12 (7)74÷6-14÷6 8
练习一 一、巧算下面各题: (1)673+288 (2)9898+203 (3)5561-4998 (4)856-(256+137) (5)825-359 (6)346+837+154-237-32-68 (7)375+219+381+225 (8)5001-247-1021-232 (9)2357-183-317-357 (10)2365-1086-214+135 (11)995+996+997+998+999 (12)799998+79997+7996+797+18 二、下面各题怎样算简便就怎样算。 (13)38×101 (14)3333×9999 (15)25×32+75×48 (16)127×102-127×2 (17)178×101-178 (18)138×4×25