2轴向拉伸与压缩

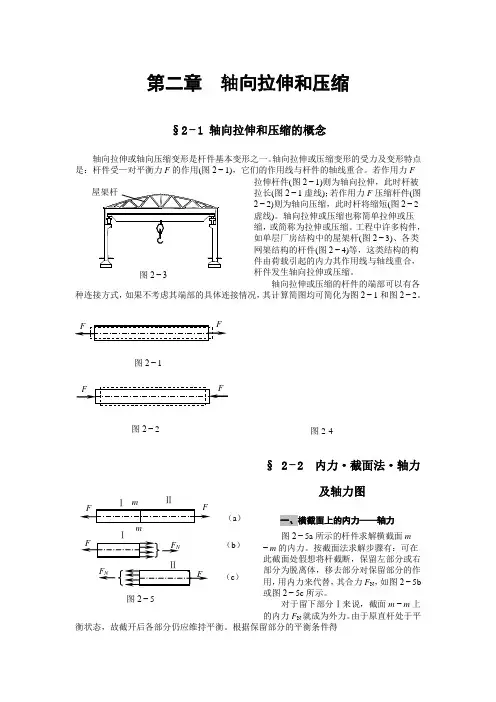
第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸，此时杆被2−1虚线)；若作用力F 压缩杆件(图(图2−2工程中许多构件，(图2−3)、各类(图2−4)等，这类结构的构2−1和图2−2。

§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。

按截面法求解步骤有：可在此截面处假想将杆截断，保留左部分或右部分为脱离体，移去部分对保留部分的作用，用内力来代替，其合力F N ，如图2−5b 或图2−5c 所示。

对于留下部分Ⅰ来说，截面m −m 上的内力F N 就成为外力。

由于原直杆处于平衡状态，故截开后各部分仍应维持平衡。

根据保留部分的平衡条件得 mF N F N（a ）（b ） （c ）图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0 (2−1)式中，F N 为杆件任一截面m −m 上的内力，其作用线也与杆的轴线重合，即垂直于横截面并通过其形心，故称这种内力为轴力，用符号F N 表示。

若取部分Ⅱ为脱离体，则由作用与反作用原理可知，部分Ⅱ截开面上的轴力与前述部分上的轴力数值相等而方向相反(图2−5b,c)。

同样也可以从脱离体的平衡条件来确定。

二、轴力图当杆受多个轴向外力作用时，如图2−7a ，求轴力时须分段进行，因为AB 段的轴力与BC 段的轴力不相同。

要求AB 段杆内某截面m −m 的轴力，则假想用一平面沿m −m 处将杆截开，设取左段为脱离体(图2−7b)，以F N Ⅰ代表该截面上的轴力。

于是，根据平衡条件∑F x ＝0，有 F F -=ⅠN负号表示的方向与所设的方向相反，即为压力。

要求B C 段杆内某截面n-n 的轴力，则在n −n 处将杆截开，仍取左段为脱离体（图2−7c ），以F N Ⅱ代表该截面上的轴力。

于是，根据平衡条件∑F x ＝0，有 02N Ⅱ=+-F F F由此得F F =N Ⅱ在多个力作用时，由于各段杆轴力的大小及正负号各异，所以为了形象地表明各截面轴力的变化情况，通常将其绘成“轴力图”(图2−7d)。

第七章轴向拉伸和压缩一、内容提要轴向拉伸与压缩是杆件变形的基本形式之一，是建筑工程中常见的一种变形。

(一)、基本概念1. 内力 由于外力的作用，而在构件相邻两部分之间产生的相互作用力。

这里要注意产生内力的前提条件是构件受到外力的作用。

2. 轴力 轴向拉（压）时，杆件横截面上的内力。

它通过截面形心，与横截面相垂直。

拉力为正，压力为负。

3. 应力 截面上任一点处的分布内力集度称为该点的应力。

与截面相垂直的分量σ称为正应力，与截面相切的分量τ称为切应力。

轴拉（压）杆横截面上只有正应力。

4. 应变 单位尺寸上构件的变形量。

5. 轴向拉（压） 杆件受到与轴线相重合的合外力作用，产生沿着轴线方向的伸长或缩短的变形，称为轴向拉（压）。

6. 极限应力 材料固有的能承受应力的上限，用σ0表示。

7. 许用应力与安全系数 材料正常工作时容许采用的最大应力，称为许用应力。

极限应力与许用应力的比值称为安全系数。

8. 应力集中 由于杆件截面的突然变化而引起局部应力急剧增大的现象，称为应力集中。

(二)、基本计算1. 轴向拉（压）杆的轴力计算求轴力的基本方法是截面法。

用截面法求轴力的三个步骤：截开、代替和平衡。

求出轴力后要能准确地画出杆件的轴力图。

画轴向拉（压）杆的轴力图是本章的重点之一，要特别熟悉这一内容。

2. 轴向拉（压）杆横截面上应力的计算任一截面的应力计算公式 AF N =σ 等直杆的最大应力计算公式 AF max N max =σ 3. 轴向拉（压）杆的变形计算虎克定律 A E l F l N =∆εσE =或 虎克定律的适用范围为弹性范围。

泊松比 εε=μ'4. 轴向拉（压）杆的强度计算强度条件塑性材料：σma x ≤[σ] 脆性材料： σt ma x ≤[σt ]σ c ma x ≤[σc ]强度条件在工程中的三类应用（1）对杆进行强度校核在已知材料、荷载、截面的情况下，判断σma x是否不超过许用值[σ]，杆是否能安全工作。

轴向拉伸与压缩的变形概念轴向拉伸与压缩是材料在受到外力作用下发生的一种变形形式。

这两种变形形式本质上都是由于材料内部的原子或分子受到外力的影响而改变了其平衡位置从而引起的。

轴向拉伸与压缩的变形概念可以通过弹簧的拉伸与压缩来加以理解。

首先我们来看轴向拉伸的变形。

当作用在弹簧两端的力朝相反方向拉伸时，弹簧会发生轴向拉伸的变形。

这是因为受到拉力的作用，弹簧内部原子或分子之间的间距增大，原本处于平衡位置的原子或分子会发生位移，使得整个弹簧长度增加。

这种拉力作用下的变形被称为轴向拉伸变形。

接下来我们来看轴向压缩的变形。

当作用在弹簧两端的力朝相同方向压缩时，弹簧会发生轴向压缩的变形。

这是因为受到压力的作用，弹簧内部原子或分子之间的间距减小，原本处于平衡位置的原子或分子会发生位移，使得整个弹簧长度减小。

这种压力作用下的变形被称为轴向压缩变形。

轴向拉伸与压缩的变形概念实际上可以通过杨氏模量来更加详细地描述。

杨氏模量是一个材料的机械特性参数，它描述了材料在轴向拉伸和压缩变形时的抵抗能力。

杨氏模量越大，材料的抵抗能力越强，抗拉强度也就越大。

相反地，杨氏模量越小，材料的抗拉强度越低。

在材料实际应用中，轴向拉伸与压缩的变形是非常常见的。

比如在建筑、桥梁、汽车、飞机等工程领域中，钢材往往被用于受力构件中，它能够在受到拉力或压力时保持较好的稳定性。

而在金属加工、塑料成型等制造领域中，轴向拉伸与压缩的变形则常常是一种设计和生产工艺。

例如在金属加工中，通过轴向拉伸可以制造出细丝，而通过轴向压缩则可以制造出坯料。

总结起来，轴向拉伸与压缩是材料在受到外力作用下发生的一种变形形式。

轴向拉伸是指材料的长度增加，原子或分子之间的间距变大；轴向压缩是指材料的长度减小，原子或分子之间的间距变小。

这两种变形形式与杨氏模量密切相关，它描述了材料在受力时的抵抗能力。

在工程和制造领域中，轴向拉伸与压缩的变形是非常常见的，它们对于材料的选择、设计和生产工艺具有重要意义。

第二章杆件的内力分析第一节杆件拉伸或压缩的内力一、轴向拉伸或压缩的概念轴向拉伸或压缩：由一对大小相等、方向相反、作用线与杆件轴线重合的外力作用下引起的，沿杆件长度发生的伸长或缩短。

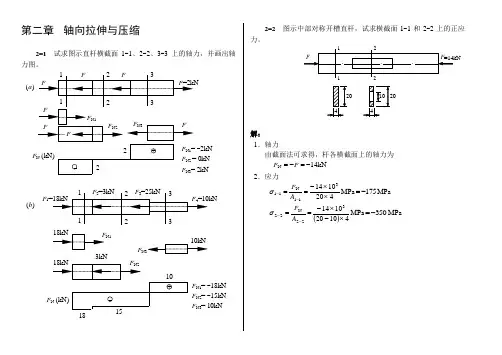
二、工程实例三、轴力轴力图1、轴力与杆轴线重合的内力合力。

轴力符号：拉伸为正，压缩为负。

∑=0X0122=-+F F N kNF F N 242212-=-=-= ∑=0X34=-N FkNF N143==任一截面上的轴力等于该截面一侧轴向载荷的代数和，轴向载荷矢量离开该截面者取正，指向该截面者取负。

2、轴力图正对杆的下方，以杆的左端为坐标原点，取平行于杆轴线的直线为x 轴，并称为基线，垂直于x 轴的N 轴为纵坐标。

正值绘在基线的上方，负值绘在基线的下方，最后在图上标上各截面轴力的大小。

注意：轴力图与基线形成一闭合曲线。

轴力图必须与杆件对齐。

在轴向集中力作用的截面上，轴力图将发生突变，其突变的绝对值等于轴向集中力的大小，而突变方向：集中力箭头向左时向上突变，集中力箭头向右时向下突变（图是从左向右画）。

例2-10第二节剪切的内力一、剪切的概念剪切：由一对相距很近、大小相等、方向相反的横向外力引起的横截面沿外力作用方向发生的相对错动。

剪切面或受剪面 m-m二、工程实例三、剪力第三节杆件扭转的内力一、扭转的概念扭转：由一对大小相等、方向相反、作用面都垂直于杆轴的力偶引起的杆的任意两个横截面绕杆轴线的相对转动。

ϕ：扭转角；γ：剪切角二、工程实例三、扭矩某一截面上的扭矩等于其一侧各外力偶矩的代数和。

外力偶矩矢量指向该截面的取负，离开该截面的取正。

四、 扭矩图在外力偶作用的截面上，扭矩图将发生突变，其突变的的绝对值等于该外力偶矩的大小，而突变方向：外力偶矩矢量方向向左的向上突变，向右则向下突变。

外力偶矩的计算公式：)(9550m N nP Mk ⋅=注意：kP 单位为kw ；n 单位为min r ；M 单位为m N ⋅第四节 梁弯曲时的内力一、 弯曲 变形的基本概念弯曲变形：由一对大小相等、方向相反，位于杆的纵向平面内的力偶引起的，杆件的轴线由直线变为曲线。