不等式及其解集

不等式的基本概念和解法不等式是数学中常见的数值比较关系表达方式之一，它描述了数之间大小关系的差异。

在解决实际问题和推导数学定理时，不等式起到了至关重要的作用。

本文将介绍不等式的基本概念和解法，帮助读者加深对不等式的理解和应用。

一、不等式的基本概念不等式是指使用不等号（如大于号、小于号）表示的数值关系，包括严格不等式和非严格不等式两种形式。

严格不等式如“<”表示不等关系，非严格不等式如“≤”表示不等关系。

在不等式中，被比较的两个数一般称为“不等式的两端”，用字母表示。

不等式的解集是使得不等式成立的数的集合。

二、不等式的解法1.代入法代入法是最常见的解不等式的方法之一。

即将候选解代入不等式，验证是否满足不等式。

通过逐个尝试的方式，找到符合不等式的解集。

例如，对于不等式3x - 4 > 5，可以逐个尝试不同的数值，如将x分别取1、2、3等代入，验证不等式是否成立，最终确定解集。

2.消元法消元法是解二元一次不等式常用的方法。

通过将不等式中的变量消去，得到一元一次不等式，进而求解。

例如，对于不等式2x + 3y > 4x - 5y，可以通过将两边的同类项合并后，消去变量y，得到3y + 5x > 2x，然后进一步化简为y > -3x。

3.图像法图像法常用于解关于一个或两个未知数的不等式。

通过将不等式转化为图形形式进行观察和判断，可快速得到不等式的解集。

例如，对于不等式y > 2x - 3，可以将不等式表示为一条直线y = 2x - 3，并通过观察直线和不等式中的“大于”关系，得出解集为直线上方的区域。

4.化简法化简法是解不等式时常用的方法之一。

通过对不等式进行化简，进而将其转化为较为简单的形式，以便求解。

例如，对于复杂的不等式2x^2 + 5x - 3 > 0，可以通过将不等式分解为(2x - 1)(x + 3) > 0，并找出方程两侧使得不等式成立的区间，进而得到解集。

不等式及其解集·要点详析
重点
1．不等式的概念
用不等号表示不等关系的式子，叫做不等式．
例如：x－1＜2，3－4＜0，3－4≠4－3，a＞0，a＜0，a2≥0等都是不等式．五种不等号的读法及意义
（1）“≠”读作“不等于”，它说明两个量之间的关系是不相等的，但不能明确哪个大哪个小；
（2）“＞”读作“大于”，表示其左边的量比右边的量大；
（3）“＜”读作“小于”，表示其左边的量比右边的量小；
（4）“≥”读作“大于或等于”，即“不小于”，表示左边“不小于”右边；
（5）“≤”读作“小于或等于”，即“不大于”，表示左边“不大于”右边．2．不等式成立与不等式不成立的意义
对于含有未知数的不等式来说，当未知数取某些值时，不等式的左、右两边符合不等号所表示的大小关系，我们就说，不等式成立；当未知数取某些数值时，不等式的左、右两边不符合不等号所表示的大小关系，我们就说，不等式不成立．3．不等式的解与不等式的解集
（1）不等式的解使不等式成立的未知数的值叫做不等式的解．
（2）不等式的解集一般地说，一个含有未知数的不等式的所有的解，组成这个不等式的解的集合，简称为这个不等式的解集．
（3）不等式的解与解集的区别与联系
不等式的解与不等式的解集是两个不同的概念，不等式的解是指满足这个不等式的未知数的某个值，而不等式的解集，是指满足这个不等式的未知数的所有的值，不等式的所有解组成了不等式的解集，解集中包括了每一个解．难点
1．不等式的解及解集．
2．不等式的解集在数轴表示的方法．。

不等式及其解集1. 不等式的概念和表示不等式是数学中一种表达式，它使用不等号（<，>，≤或≥）来表示两个数或两个代数式之间的大小关系。

不等式可以包含一个或多个未知数，并且可以包含常数和其他数学运算。

不等式的一般形式如下：p(x) < q(x)其中p(x)和q(x)是多项式函数，表示式子的左侧和右侧。

不等式的解集是满足不等式的x的值的集合。

2. 一元一次不等式一元一次不等式是指只包含一个未知数x，并且最高次数为一次的不等式。

例如：ax + b < 0其中a和b是常数。

要求解这个不等式，我们可以按照以下步骤进行：1.将不等式转化为等式：ax + b = 02.求解这个等式的解x_0。

3.根据x_0的位置确定不等式的解集。

假设x_0表示等式的解。

•如果a > 0，则解集为(x, −∞)•如果a < 0，则解集为(−∞, x)3. 一元二次不等式一元二次不等式是指只包含一个未知数x，并且最高次数为二次的不等式。

例如：ax^2 + bx + c > 0其中a，b和c是常数。

要求解这个不等式，我们可以按照以下步骤进行：1.将不等式转化为等式：ax^2 + bx + c = 02.求解这个等式的解集{x_1, x_2}。

3.根据x_1和x_2的位置确定不等式的解集。

假设x_1和x_2表示等式的解。

•如果a > 0，则解集为(−∞, x_1) ∪ (x_2, +∞)•如果a < 0，则解集为(x_1, x_2)4. 多元不等式多元不等式是指含有多个未知数的不等式。

解决多元不等式的方法通常是通过图形、代数方法或数值方法。

例如：考虑以下两个不等式：ax + by ≥ cdx + ey < f可以使用图形方法将它们表示在坐标系中，并找到满足这两个不等式的区域。

通过确定这些区域的交集，可以获得满足所有条件的解集。

5. 不等式解集的表示和性质不等式解集通常用集合表示法来表示，例如：S = {x | p(x) < q(x)}其中，S表示满足不等式的x的集合，p(x)和q(x)分别代表不等式的左侧和右侧。

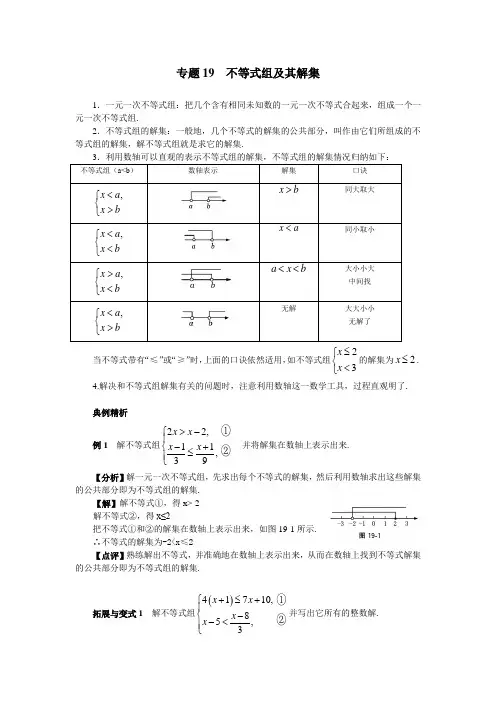
专题19 不等式组及其解集1．一元一次不等式组：把几个含有相同未知数的一元一次不等式合起来，组成一个一元一次不等式组.2．不等式组的解集：一般地，几个不等式的解集的公共部分，叫作由它们所组成的不 等式组的解集，解不等式组就是求它的解集. 不等式组（a <b ）数轴表示 解集 口诀 同大取大 同小取小 大小小大 中间找 无解 大大小小 无解了当不等式带有“≤”或“≥”时，上面的口诀依然适用，如不等式组的解集为.4.解决和不等式组解集有关的问题时，注意利用数轴这一数学工具，过程直观明了.典例精析例1 解不等式组 并将解集在数轴上表示出来.【分析】解一元一次不等式组，先求出每个不等式的解集，然后利用数轴求出这些解集的公共部分即为不等式组的解集.【解】解不等式①，得x>-2解不等式②，得x≤2把不等式①和②的解集在数轴上表示出来，如图19-1所示.∴不等式的解集为-2<x ≤2【点评】熟练解出不等式，并准确地在数轴上表示出来，从而在数轴上找到不等式解集的公共部分即为不等式组的解集.拓展与变式1 解不等式组并写出它所有的整数解.,x a x b<⎧⎨>⎩x b >,x a x b <⎧⎨<⎩x a <,x a x b >⎧⎨<⎩a xb <<,x a x b <⎧⎨>⎩23x x ≤⎧⎨<⎩2x ≤22,11,39x x x x >-⎧⎪-+⎨≤⎪⎩①②()41710,85,3x x x x +≤+⎧⎪⎨--<⎪⎩①②拓展与变式2 不等式组的所有整数解的和是 . 拓展与变式3 若|x+1|=x+1，|2x-7|=7-2x ，则满足条件的所有非负整数x 有 .【反思】根据题意列出不等式（组），解出不等式组从而找出符合条件的解，注意非负整数即自然数，也就是0和正整数.例2 如果a>2，那么不等式组的解集为 ，的解集为 . 【分析】把每个不等式的解集表示在数轴上（或用口诀），结合数轴找不等式组的解集.【解】把不等式的解集表示在数轴上，不等式组表示在数轴上如图19-2所示，可知解集为x >a .不等式组表示在数轴上如图19-3所示， 可知解集为2<x ≤a .【点评】利用数轴上的数越往右越大，在数轴上找好数约位置，结合数轴找到不拓展与变式4 （1）已知关于x 的不等式组的解集为x ≥2，则a 的取值范围是 .（2）已知关于x 的不等式组有解，则a 的取值范围是 . 拓展与变式5 已知关于x 的不等式组的解集为0<x <2，求m -n 的值.拓展与变式6 解关于x 的不等式组34125x +-≤<,2x a x >⎧⎨>⎩,2x a x ≤⎧⎨>⎩,2x a x >⎧⎨>⎩,2x a x ≤⎧⎨>⎩,2x a x >⎧⎨≥⎩,2x a x <⎧⎨>⎩2,11x m n x m +>+⎧⎨-<-⎩①②0,12.23x a x x x -≥⎧⎪-+⎨+>⎪⎩①②拓展与变式7 已知关于x 的不等式组的整数共有3个，求a 的取值范围.拓展与变式8 定义新运算：对干任意实数a ，b 都有a #b =ab -a -b +1，等式右边是通常的加法减法及乘法运算.例如：2#4=2×4-2-4+1=3.请根据上述知识解决问题：若3#x 的值大于4而不大于m 时，恰有两个整数解，求m 的取值范围.【反思】解决含参数的不等式组问题，数形结合必不可少，同时要注意等号能否取到，可将取等号的值代入原题中检验.专题突破1.不等式组的整数解有（ ）. A. 1个 B. 2个 C. 3个 D. 4个0,321x a x -≥⎧⎨-≥-⎩①②24,241x x x x ≤+⎧⎨+<-⎩2.不等式组的解集是x>1，则m 的取值范围是 .3.解不等式组并将不等式组的解集在数轴上表示出来.4.某旅行社某天有空房10间，当天接待了一个旅行团，当每个房间只住3人时，有一个房间的住宿情况是不满也不空.若旅行团的人数为偶数，问：旅行团共有多少人?5.关于x 的不等式组有2个整数解，求a 的取值范围.551,1x x x m +<+⎧⎨-≥⎩()5623,3513,44x x x x -≤+⎧⎪⎨-<-⎪⎩①②()2331,324x x x x a <-+⎧⎪⎨+>+⎪⎩①②。

不等式的基本性质及其解集一、不等式的性质1．不等式的两边都加上（或减去）同一个数或整式，不等号的方向不变． c a b a +⇒> ca b a c b +⇒<+, c b +2．不等式的两边都乘以（或除以）同一个正数，不等号的方向不变。

若：0,>>c b a ，可得ac bc ．3．不等式的两边都乘以（或除以）同一个负数，不等号的方向改变．若ac c b a ⇒<>0, bc ． 二．不等式的解集1．定义：一般的，一个含有未知数的不等式的所有解，组成这个不等式的解的集合，简称这个不等式的解集.2．解与解集的联系： 解集和解那个的范围大.（解是指个体，解集是指群体） 3．不等式解集的表示方法. 1-≤x ①用不等式表示。

如1-≤x 或x <-1等。

x <②用数轴表示.（注意实心圈与空心圈的区别） 4.解一元不等式的步骤：去分母，去括号，移项，合并同类项，系数化为1，注意是否需要变号。

典型例题例1.①如果)2(2)2(-<-m x m 的解集为2>x ，求m 的取值范围. ②不等式a x <2的解集为7<x ，求a 的值.例2.（1）如果关于x 的方程x m m x +-=+2432的解为大于4的数，求m 的取值范围.（2）已知不等式03≤-a x 的正整数解恰是1，2，3，求a 的取值范围.例3．直线l 1：y ＝k 1x ＋b 与直线l 2：y ＝k 2x 在同一平面直角坐标系中的图象如图所示，则关于x 的不等式k 1x ＋b ＞k 2x 的解为（ ）。

A 、x ＞－1B 、x ＜－1C 、x ＜－2D 、无法确定 例4．（1）若0)2(32=--+-k y x x 中，y 为非负数，求k 的取值范围．思考题．设c b a ,,均为正数，若ac bc b a b a c +<+<+，试确定c b a ,,三个数的大小．y k 2x(第3题图)【经典练习】一、选择题（每小题2分，共36分）1、“x 的2倍与3的差不大于8”列出的不等式是（ ） A 、2x －3≤8 B 、2x －3≥8 C 、2x －3＜8 D 、2x －3＞82、下列不等式一定成立的是（ ） A 、5a ＞4aB 、x +2＜x +3C 、－a ＞－2aD 、aa 24> 3、如果x ＜－3，那么下列不等式成立的是（ ） A 、x 2＞－3x B 、x 2≥－3x C 、x 2＜－3x D 、x 2≤－3x 4、不等式－3x +6＞0的正整数解有（ ） A 、1个 B 、2个 C 、3个 D 、无数多个 *5、若m 满足|m |＞m ，则m 一定是（ ） A 、正数 B 、负数 C 、非负数 D 、任意有理数 6、在数轴上与到原点的距离小于8的点对应的x 满足（ ） A 、－8＜x ＜8 B 、x ＜－8或x ＞8 C 、x ＜8 D 、x ＞8**7、要使函数y =（2m －3）x +（3n +1）的图象经过x 、y 轴的正半轴，则m 与n 的取值应为（ ）A 、m ＞23，n ＞－31B 、m ＞3，n ＞－3C 、m ＜23，n ＜－31D 、m ＜23，n ＞－31*8、 下列说法中，正确的有（ ）.① 若0ab <，则0,0;a b <<②若0,0a b <>，则0ab <；③若22,a b m m <则a b <；④若a b <，则22am bm <;⑤若0a b <<，则0a b +<；⑥若0a b +<，则0a b <<.A 、4个B 、3个C 、2个D 、1个 9、 下列说法正确的是（ ）. A 、5是不等式x+5＞10的解集 B 、x ＜5是不等式x-5＞0的解集 C 、x ≥5是不等式-x ≤-5的解集D 、x ＞3是不等式x-3≥0的解集10、 若a-b ＜0，则下列各式中一定正确的是（ ）.A 、a ＞bB 、ab ＞0C 、ab＜0 D 、-a ＞-b11 不等式5x-1≤24的正整数解有（ ）.A 、4个B 、5个C 、6个D 、无限多个 **12 实数b 满足|b |<3，并且实数a 使得a <b 恒成立，则a 的取值范围是（ ） A 、小于或等于3的实数 B 、 小于或等于－3的实数 C 、小于－3的实数 D 、 小于3的实数 13、 若4x <-，则下列不等式中正确的是（ ）. A ．x 2≥－4x B 、x 2≤－4x C 、 x 2>－4x D 、 x 2<－4x*14、关于x 的方程2435x a x b++=的解不是负数，则a 与b 的关系是（ ） A 、35a b > B 、 b ≥53aC 、5a =3bD 、5a ≥3b 15、在不等式100>5x 中，能使不等式成立的x 的最大正整数值为（ ）. A 、18 B 、19 C 、20 D 、21 16、下列不等式中，错误的是（ ）. A 、57-<-B 、5>3C 、0a 12>+D 、a a ->**17、已知5x －m ≤0只有两个正整数解，则m 的取值范围是（ ） A 、10<m <15 B 、10≤m ≤15 C 、10<m ≤15 D 、10≤m <15 18、下列各式中，是一元一次不等式的是（ ）. A 、1y x 21<- B 、02x 3x 2>+- C 、2x141x 2+=+ D 、x 61x 31x 21>+二、填空题（每小题2分，共36分）1、不等式6－2x ＞0的解集是________.2、当x ________时，代数式523--x 的值是非正数. 3、当m ________时，不等式（2－m ）x ＜8的解集为x ＞m-28. 4、若x =23+a ，y =32+a ，且x ＞2＞y ，则a 的取值范围是________.5、已知三角形的两边为3和4，则第三边a 的取值范围是________.6、已知一次函数y =（m +4）x －3+n （其中x 是自变量），当m 、n 为________时，函数图象与y 轴的交点在x 轴下方.*7、某种商品的价格第一年上升了10%，第二年下降了（m －5）%（m ＞5）后，仍不低于原价，则m 的值应为________.8、5m-3是非负数，用不等式表示为______. 9、不等式238654x--<-<-的解集为______.10、当a b >，则2ab b <成立的条件是______.*11、明明的语文、外语两科的平均分为m 分，若使语文、外语、数学三科的平均分超过n 分，则数学分数a （分）应满足的关系式是_________.（m >n ） 12、设a ＜b ，用“＜”或“＞”|号填空：11(1)_____;(2)100_____100;22(3)1.5_____1.5;(4)_____.1212a b a b a ba b --++--13、不等式的性质：（1）如果a>b, 那么a+c b+c. （2）如果m>n, p>0, 那么mp np. （3） . 14、若-3x +4<-2x -5,则-x ______-9.15、已知直线y=kx+b 经过点（2，0），且k <0，则当x ______时，y <0. 16、不等式x <3的非负整数解是________.17、不等式|x |-2≤3的正整数解是____________.18、在2y 2-3y +1>0, y 2+2y +1=0,-6<-2, 27ab<2, 2312x x +- ,2103y y --<,7x +5≥5x +6中, 一元一次不等式有_____个,它们是_____________________.三、解答题1、解下列不等式，并把解集在数轴上表示出来：（每题4分共16分） （1）3（1-x ）-2（x+8）<2； （2）3（x+3）-5（x-1） ≥7； （3）132+-x ≤42+x ；（4）)69(6123--x x ≥7+x ．3、（6分）在“科学与艺术”知识竞赛的预选赛中共有20道题，对于每一道题，答对得10分，答错或不答扣5分，总得分不少于80分者通过预选赛。

不等式复习一一、双基回忆1、不等式：用等号〔＜、≤、＞、≥〕连接起来的式子，叫做不等式。

〔1〕用不等式表示：①x与1的差是负数：；②a的1/2与b的3倍大于2 ；③x、y的平方和是非负数。

2、不等式的解和解集使不等式成立的未知数的值叫做不等式的解。

一个含有未知数的不等式的所有解，组成这个不等式的解集。

注意：解集包括解，所有的解组成解集；解是一个数，解集是一个范围。

〔2〕判断以下说法是否正确：①4是不等式x＋3＞6的解；②不等式x＋2＞1的解是x＞－1；③3是不等式x＋2＞5的一个解；④不等式x＋1＜4的解集是x＜2.3、一元一次不等式：含有一个未知数并且未知数的次数是1的不等式叫做一元一次不等式。

〔3〕以下不等式是一元一次不等式的是.①3x+5=1；②2y-1≤5；③2/x+1＞3；④5+2＜8;⑤3+x2≥x.4、不等式的性质：〔1〕不等式两边加〔或减〕同一个数〔或式子〕，不等号的方向不变.即如果a＞b，那么a±c＞b±c.〔2〕不等式两边乘〔或除以〕同一个正数，不等号的方向不变.即如果a＞b，c＞0，那么ac ＞bc(或a/c＞b/c).〔3〕不等式两边乘〔或除以〕同一个负数，不等号的方向改变.即如果a＞b，c＜0，那么ac ＜bc(或a/c＜b/c).注意：①不等式的性质与等式的性质有相通之处，又有不同之点；②不等式的性质是解不等式的依据。

〔4〕a＞b，填空：①a+3 b+3,②2a 2b,③- a/3 －b/3，④a－b 0.5、解一元一次不等式〔5〕解一元一次不等式: 2x≥5x+6，并在数轴上表示解集。

二例题导引例1 判断正误：①假设a＞b,那么 ac2＞bc2；②假设ac2＞bc2,那么a＞b；③假设2 a+1＞2b+1,那么a＞b；④假设a＞b,那么1－2 a＞1－2b.例2 解以下不等式，并把它们的解集在数轴上表示出来。

〔1〕3〔1－x〕＜2(x+9); (2)112132x x ---≤.例3 a取什么自然数时，关于x的方程2－3x= a解是非负数？例4 小明和小丽决定把省下来的零用钱存起来，这个月小明顾虑了168元，小丽顾虑了85元，从下个月开始小明每月顾虑16元，而小丽每月存25元，问几个月后小丽的存款数能超过小明？三、练习提高夯实根底1、x的1/2与5的差不小于3，用不等式表示为。

不等式的基本性质及其解集【知识要点一】等式与不等式的基本知识对照表：等式不等式两边都加上（或减去）同一个数或同一个整式，所得结果仍是等式两边都加上（或减去）同一个数或同一个整式，不等号的方向不变.两边都乘以（或除以）同一个数（除数不能是0），所得结果仍是等式 两边都乘以（或除以）同一个正数，不等号的方向不变两边都乘以（或除以）同一个负数，不等号方向改变【知识要点二】1.不等式的解：能使不等式成立的未知数的值.2.不等式的解集：一个含有未知数的不等式的所有解.3.解不等式：求不等式的解集的过程叫做解不等式.4.不等式解集的表示方法：a.用不等式表示：如32≥+x 的解集表示为：1≥xb.在数轴上直观表示如图： 如：a x >b x ≤b x a <≤ 【经典例题】例1.将下列不等式化为""a x >或""a x <形式（1）97<-x（2）145->x x （3）231>x （4）155<-xabba例2.在数轴上表示下列不等式的解集 （1）3-≥x （2）211<x （3）212321<≤-x （4）2||<x例3.求不等式212-≥-x 的非负整数解.练习：求出不等式431≤-≤-x 的解集，并求出其整数解．例4．已知02≤+x ，化简13222+-++x x例5．指出下列不等式成立的条件1．当0>a 时，0>ab 2．当0>a 时，0<ab3．当0<a 时，0<ab 4．当0<a 时，0>ab例6.如果关于x 的方程x m m x +-=+2432的解为大于4的数，求m 的取值范围. 练习：1. ①如果)2(2)2(-<-m x m 的解集为2>x ，求m 的取值范围. ②不等式a x <2的解集为7<x ，求a 的值.2. 如果关于x 的方程323bx a x +=-的解是正整，求a 与b 的关系.例7.已知不等式03≤-a x 的正整数解恰是1，2，3，求a 的取值范围.☆基础探究☆1.由y x >得到ay ax <的条件是（ ） A 、0>aB 、0≥aC 、0<aD 、0≤a2.若m 为有理数，下列不等式关系不一定成立的是（ ）A 、m m +>+79B 、m m -<-43C 、m m 46>D 、0||4≥m3.已知b a ,两数在数轴上对应的点如图所示，下列结论正确的是（ ） A 、b a > B 、0<ab C 、0>-a b D 、0>+b a4.下列各数0,3,2.5,,4,21π-中,能使不等式12>-x 成立的是（ ） A 、-4，π，5，2 B 、π，5，2 C 、π，5，2，3 D 、21，0，3 5.不等式143<x 的非负整数解是（ ） A 、无数个B 、1C 、0，1D 、1，26.下列四个结论：（1）4是不等式63>+x 的解；（2）4>x 是不等式63>+x 的解集； （3）3是不等式63≥+x 的解；（4）3≥x 是不等式63≥+x 的解集，其中正确的是（ ） A 、1个B 、2个C 、3个D 、4个7.如果b a >，用"">或""<填空 （1）a 2 b 2 （2）a 3- b 3- （3）a - b - （4）2a 2b（5）35a -b 35- （6）3+a 3+b8.如果b ax >，02<ac ，则xab 9.不等式21131<-x 的解集是 ，12≤-x 的正整数解为 . 10.若不等式a x <6的解集为3<x ，则a 的值为 .11.如果不等式1)1(+>+a x a 的解集为1<x ，那么a 必须满足 . 12.根据不等式性质，把下列不等式化成a x >或a x <的形式 （1）534+>x x（2）3132-<x （3）172<-x （4）123->-x xba 0☆综合能力提升☆ 13.在数轴上表示下列解集（1）大于-3而小于4的数 （2）所有不小于-4的数（3）所有不大于3的数 （4）绝对值小于3的数14.已知关于4152435+=-m m x 的解是非负数，求m 的取值范围，并在数轴上表示出来.15.已知不等式12≤-m x 的正整数解恰是1，2，求m 的取值范围.课后巩固1.设0<a ，则下列各式中不成立的是（ ） A 、43+<+a aB 、a a 43<C 、a a -<-43D 、43aa ->-2.若4-<x ，则下列不等式成立的是（ ）A 、x x 42->B 、x x 42-≥C 、x x 42-<D 、x x 42-≤3.下列按要求列出的不等式中，不正确的是（ ）A 、m 不是负数，则0≥mB 、m 是非大于0的数，则0≤mC 、m 不小于-1，则1-≥mD 、m 是非正数，则0<m4.与063<-x 不同解的不等式为（ ） A 、713<+xB 、63->-xC 、126<xD 、63-<-x5.下列说法中，错误的是（ ）A 、不等式13<x 的整数解有无限多个B 、不等式52<x 的整数解有有限个C 、不等式82<-x 的解集为4->xD 、不等式153<x 的正整数解有有限个 6．不等式1)2(>-x m 的解集为21-<m x ，则有（ ） A 、2>mB 、2<mC 、3>mD 、3<m7．下列不等式中，解集为全体实数的是（ ） A 、122+-x x >0 B 、02>x C 、x x 131<- D 、111<+-x x 8.若n m >时，m a 2n a 29.若22bc ac >，则a 3- b 3-10.若24ba ->-，则a b 2 11.不等式13<-x 的正整数解是 . 12.不等式5.5-≥x 的负整数解是 ．13.如果关于x 的方程02=+kx 的根是3，那么不等式8)2(->+x k 的解集是什么？请你在数轴上表示出来．14.如果不等式x m x 253-<+没有正数解，求m 的值．15.关于x 的方程1223+=+m x 的解为正数，求m 的取值范围.16.不等式a x <+32的正整数解恰为1，2，求m 的取值范围.。

不等式及不等式基本性质 一．不等式 定义：用不等号连接起来的式子叫做不等式． （1）常见的不等号有五种： “≠”、 “>” 、 “<” 、 “≥”、 “≤”． （2）列不等式注意找到问题中不等关系的词，如： 正数(＞0) 负数（＜0） 非正数（≤0） 非负数（≥0） 超过(＞0) 不足（＜0） 至少（≥0） 至多（≤0） 不大于（≤0） 不小于（≥0） （3）不等号具有方向性，其左右两边不能随意交换;但a ＜b 可转换为b ＞a ，c ≥d 可转换为d ≤c 。

例1、用不等式表示 (1)a 与1的和是正数; (2)y 的2倍与1的和大于3; (3)x 的一半与x 的2倍的和是非正数; (4)c 与4的和的30%不大于-2; (5)x 除以2的商加上2,至多为5;(6)a 与b 两数的和的平方不可能大于3.例2：判断下列哪些式子是不等式，哪些不是不等式。

①32>-；②21x ≤；③21x -；④s vt =；⑤283m x <-；⑥124x x->-；⑦38x ≠；⑧5223x x -≈-+；⑨240x +>；⑩230xπ+>。

练习：用不等式表示：①x 的平方是非负数： ②a 不大于b ： ③x 的3倍与－2的差是负数： ；④长方形的长为x cm ，宽为10cm ，其面积不小于200cm 2： 二．不等式的解与解集(1)不等式的解：使不等式成立的未知数的值，叫做不等式的解． 解析:不等式的解可能不止一个.例3、下列各数中,哪些是不等是x+1<3的解?哪些不是? -3,-1,0,1,1.5,2.5,3,3.5(2)不等式的解集：一个含有未知数的不等式的解的全体，叫做不等式的解集． 不等式的解集。

不等式的解集可以在数轴上直观的表示出来，具体表示方法是:①确定边界点。

解集包含边界点，是实心圆点； 不包含边界点，则是空心圆圈； ②确定方向：大向右，小向左。