几何公差定义(中文)
- 格式:xls
- 大小:226.00 KB
- 文档页数:20
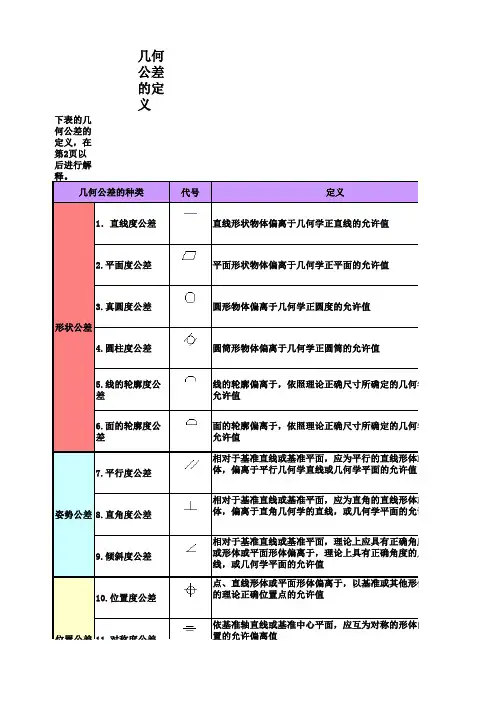



几何公差定义几何公差是指在工程制图和工程设计中,用于表达零件尺寸和形状误差的一种标准。
它通过一系列数值来描述零件在制造过程中所允许的尺寸变化范围,以确保零件的功能和互换性。
本文将介绍几何公差的定义、分类和应用。
一、几何公差的定义几何公差是指在制造和装配过程中,允许零件尺寸和形状发生变化的范围。
它是一种用于描述零件形状和位置误差的数值表示方法,可以确保零件在装配后能够满足要求的功能和性能。
二、几何公差的分类根据几何公差的性质和作用,可以将其分为以下几类:1. 形位公差:形位公差用于描述零件的形状和位置关系。
它包括平行度、垂直度、同轴度等指标,用于确保零件的平面度、垂直度和同轴度满足要求。
2. 尺寸公差:尺寸公差用于描述零件的尺寸变化范围。
它包括直径公差、间距公差、倾斜度公差等指标,用于确保零件的尺寸满足要求。
3. 表面公差:表面公差用于描述零件的表面质量和形状误差。
它包括粗糙度、平面度、圆度等指标,用于确保零件的表面光洁度和形状精度满足要求。
三、几何公差的应用几何公差在工程制图和工程设计中起着重要的作用,它可以确保零件在制造和装配过程中满足要求的功能和性能。
具体应用如下:1. 工程制图:在工程制图中,几何公差被用于描述零件的尺寸和形状误差。
通过在图纸上标注几何公差,可以使制造工人和装配工人清楚地了解零件的尺寸和形状要求,从而保证零件的制造和装配质量。
2. 工程设计:在工程设计中,几何公差被用于确定零件的尺寸和形状要求。
通过合理地设置几何公差,可以在满足功能和性能要求的前提下,尽量减小零件的制造成本和装配难度。
3. 制造控制:在零件制造过程中,几何公差被用于控制零件的尺寸和形状误差。
通过对制造工艺和设备进行优化,可以使零件的尺寸和形状误差控制在允许范围内,从而保证零件的制造质量。
4. 装配调整:在零件装配过程中,几何公差被用于调整零件的相对位置和形状关系。
通过合理地调整零件的位置和形状,可以使零件在装配后满足要求的功能和性能。


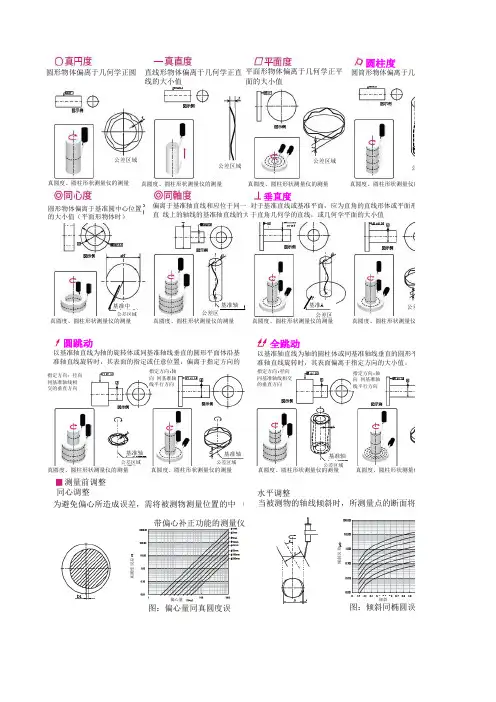


几何尺寸和公差80个入门讲解一、概述在工程设计和制造领域,几何尺寸和公差是非常重要的概念。
它们直接影响着产品的质量和可制造性,因此对其理解和运用至关重要。
本文将系统地介绍几何尺寸和公差的基本概念和应用方法,希望能为初学者提供全面的入门指导。
二、几何尺寸的定义1. 几何尺寸是指零件的形状、位置和轮廓的尺寸大小和位置关系,用几何图形和数字表示。
它可以是直线、角度、平面、曲线等各种形态。
2. 几何尺寸包括线性尺寸、角度尺寸、直线、平面等各种尺寸,通常用符号和数字表示。
3. 几何尺寸的意义在于描述零件的形状和位置,为设计和制造提供基础数据。
三、公差的定义1. 公差是指零件尺寸允许的最大偏差和最小偏差之间的差值范围。
它是为了保证零件在设计尺寸范围内能够正常工作而设置的。
2. 公差可以分为一般公差、限制公差和无限制公差等不同类型。
3. 公差的作用在于控制零件的尺寸精度和质量,保证其在装配和使用过程中可以正常运行。
四、几何尺寸和公差的关系1. 几何尺寸和公差是密切相关的,几何尺寸描述了零件的实际尺寸和形状,而公差则规定了这些尺寸的允许偏差范围。
2. 几何尺寸和公差之间的关系是相辅相成的,只有合理设置公差才能保证几何尺寸的精度和质量。
3. 几何尺寸和公差的理解和应用需要结合具体的设计和制造要求,综合考虑材料、工艺、装配和使用等方面的因素。
五、几何尺寸和公差的标注方法1. 几何尺寸和公差通常是通过特定的符号和数字来标注的,符号包括直线、平面、圆、圆孔、角度等各种图形和符号。
2. 标注应该清晰、准确、规范,要符合相关的国家标准和行业规范。
3. 标注应该包括基本尺寸、公差尺寸、零件的形状和位置等必要信息,以便于人们理解和使用。
六、几何尺寸和公差的应用范围1. 几何尺寸和公差广泛应用于机械制造、汽车制造、航空航天、船舶制造、电子电器、仪器仪表等各个领域。
2. 在不同的领域和行业中,几何尺寸和公差的标准和要求可能会有所不同,需要根据实际情况来进行理解和应用。


几何公差总结彻底理解几何公差的符号及管控意义,并正确理解尺寸公差的概念,是一件非常困难的事情。
接下来,我们聚焦几何公差的“读取”与“测量”,以最通俗易懂的语言进行细致解说。
No.1什么是几何公差?ISO将几何公差定义为“Geometrical product specifications (GPS)−Geometrical tolerancing−Tolerancing of form, orientation, location and run-out”。
换言之,“几何特性”指的是物体的形状、大小、位置关系等,“公差”则是“容许误差”。
“几何公差”的特点,是不仅定义尺寸,还会定义形状、位置的容许误差。
1、尺寸公差与几何公差的区别:设计图纸的标注方法,大致可分为“尺寸公差”与“几何公差”这两类。
尺寸公差管控的是各部分的长度。
而几何公差管控的则是形状、平行度、倾斜度、位置、跳动等。
▲尺寸公差图纸▲几何公差图纸意为“请进行对示面(A)的‘平行度’不超过‘0.02’的加工”。
2、几何公差的优点:为什么需要标注几何公差呢?举个例子,设计者在订购某板状部件时,通过尺寸公差进行了如下标示。
但是根据上述图纸,生产方可能会交付如下所示的部件。
这样的部件会成为不适合品或不良品。
究其原因,就是没有在图纸上标注平行性。
相应的责任不在于加工业者,在于设计者的公差标示。
用几何公差标注同一部件的图纸,可得到如下所示的设计图。
该图在尺寸信息的基础上,追加了“平行度”、“平面度”等几何公差信息。
这样一来,就能避免因单纯标注尺寸公差而导致的问题。
差标注同一部件的图纸,可得到如下所示的设计图。
该图在尺寸信息的基础上,追加了“平行度”、“平面度”等几何公差信息。
这样一来,就能避免因单纯标注尺寸公差而导致的问题。
综上所述,几何公差的优点,就是能够正确、高效地传达无法通过尺寸公差来体现的设计者意图。
3、独立原则尺寸公差与几何公差管控的公差不同。
几何公差的知识点总结几何公差的概念在数学中是非常重要的,它不仅可以帮助我们理解数列的性质,还可以应用于各种实际问题中。
在这篇文章中,我们将对几何公差的相关知识点进行总结和讨论,希望能够帮助读者更好地理解和运用这一概念。
1. 几何公差的定义在等差数列中,如果相邻两项的差值为一个常数d,那么这个常数d就是数列的公差。
类似地,在等比数列中,如果相邻两项的比值为一个常数q,那么这个常数q就是数列的公比。
这个常数q也称为数列的几何公差。
例如,对于等比数列1,2,4,8,16,公比为2,即相邻两项的比值都为2。
因此,2就是这个数列的几何公差。
2. 几何公差的性质几何公差和等差公差一样,具有一些重要的性质,这些性质在数学中有着广泛的应用。
首先,几何数列中的任意一项可以表示为首项乘以公比的幂。
具体而言,如果首项为a,公比为q,那么第n项可以表示为an = a * q^(n-1)。
这个公式可以帮助我们求解数列中任意一项的值。
其次,对于几何数列来说,如果公比大于1,那么数列将呈指数增长的趋势;如果公比在0和1之间,那么数列将呈指数衰减的趋势。
这一性质可以帮助我们分析数列的变化规律。
另外,对于几何数列,如果前n项之和为Sn,那么Sn = a * (1 - q^n) / (1 - q)。
这个公式可以帮助我们求解数列前n项之和的数值。
3. 几何公差的应用几何公差在数学中有着广泛的应用,它不仅可以用于解决数列问题,还可以应用于各种实际问题中。
首先,在数学中,我们经常需要对数列进行求和,计算等差数列的和是非常简单的,只需要利用数列求和公式即可。
但是对于等比数列来说,求解前n项之和就需要用到几何数列的性质和公式。
因此,几何公差的知识对于求解数列的和具有重要的意义。
其次,几何公差还可以应用于各种实际问题中。
例如在金融领域,复利计算就是一个典型的几何数列应用。
又如在生物学中,生物种群的增长规律也可以用等比数列来进行描述。
因此,几何公差的知识在实际问题的建模和求解中具有广泛的应用。