多面体与球的接切(ppt)

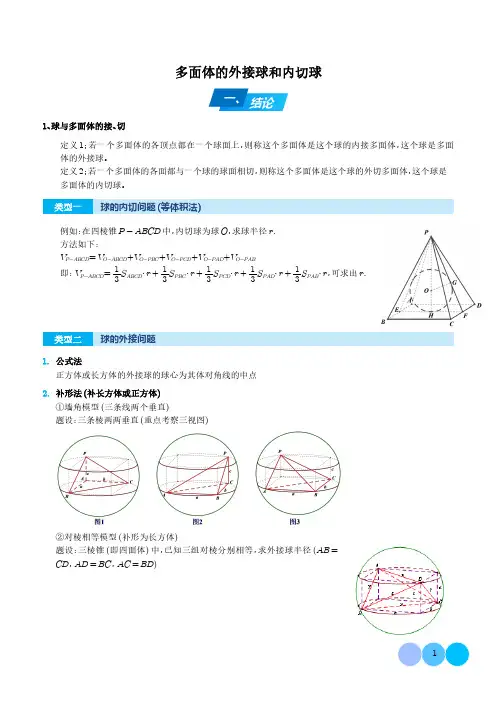
多面体的外接球和内切球一、结论1、球与多面体的接、切定义1；若一个多面体的各顶点都在一个球面上，则称这个多面体是这个球的内接多面体，这个球是多面体的外接球。

定义2；若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是多面体的内切球。

球的内切问题(等体积法)例如：在四棱锥P -ABCD 中，内切球为球O ，求球半径r .方法如下：V P -ABCD =V O -ABCD +V O -PBC +V O -PCD +V O -PAD +V O -PAB即：V P -ABCD =13S ABCD ⋅r +13S PBC ⋅r +13S PCD ⋅r +13S PAD ⋅r +13S PAB ⋅r ，可求出r .球的外接问题1.公式法正方体或长方体的外接球的球心为其体对角线的中点2.补形法(补长方体或正方体)①墙角模型(三条线两个垂直)题设：三条棱两两垂直(重点考察三视图)②对棱相等模型(补形为长方体)题设：三棱锥(即四面体)中，已知三组对棱分别相等，求外接球半径(AB =CD ，AD =BC ，AC =BD )3.单面定球心法(定+算)步骤：①定一个面外接圆圆心：选中一个面如图：在三棱锥P-ABC中，选中底面ΔABC，确定其外接圆圆心O1(正三角形外心就是中心，直角三角形外心在斜边中点上，普通三角形用正弦定理定外心2r=asin A)；②过外心O1做(找)底面ΔABC的垂线，如图中PO1⊥面ABC,则球心一定在直线(注意不一定在线段PO1上)PO1上；③计算求半径R:在直线PO1上任取一点O如图：则OP=OA=R，利用公式OA2=O1A2+OO12可计算出球半径R.4.双面定球心法(两次单面定球心)如图：在三棱锥P-ABC中：①选定底面ΔABC，定ΔABC外接圆圆心O1②选定面ΔPAB，定ΔPAB外接圆圆心O2③分别过O1做面ABC的垂线，和O2做面PAB的垂线，两垂线交点即为外接球球心O.二、典型例题1(2023春·湖南湘潭·高二统考期末)棱长为1的正方体的外接球的表面积为()A.3π4B.3πC.12πD.16π【答案】B【详解】解：易知，正方体的体对角线是其外接球的直径，设外接球的半径为R，则2R=12+12+12=3，故R=3 2．所以S=4πR2=4π×322=3π．故选：B．【反思】本例属于正方体外接球问题，其外接球半径公式可直接记忆.2(2023春·湖南长沙·高三长沙一中校考阶段练习)在四面体PABC中，PA⊥AB，PA⊥AC，∠BAC= 120°，AB=AC=AP=2，则该四面体的外接球的表面积为()A.12πB.16πC.18πD.20π【答案】D【详解】因为PA⊥AB，PA⊥AC，AB∩AC=A,AB,AC⊂平面ABC,所以PA⊥平面ABC.设底面△ABC的外心为G，外接球的球心为O，则OG⊥平面ABC，所以PA⎳OG.设D为PA的中点，因为OP=OA，所以DO⊥PA.因为PA⊥平面ABC，AG⊂平面ABC,所以PA⊥AG，所以OD⎳AG.因此四边形ODAG为平行四边形，所以OG=AD=12PA=1.因为∠BAC=120°，AB=AC=2，所以BC=AB2+AC2-2AB⋅AC cos∠BAC=4+4-2×2×2×-1 2=23,由正弦定理，得2AG=2332=4⇒AG=2.所以该外接球的半径R满足R2=OG2+AG2=5,故该外接球的表面积为S=4πR2=20π.故选:D.【反思】本例属于单面定球心问题①用正弦定理求出ΔABC外心G；②过G做平面ABC的垂线，则外接球球心O在此垂线上；③通过计算算出半径.3(2023秋·湖南娄底·高三校联考期末)《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1000多年．在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图P-ABCD 是阳马，PA⊥平面ABCD，PA=5，AB=3，BC=4．则该阳马的外接球的表面积为()A.1252π3B.50π C.100π D.500π3【答案】B【详解】因PA⊥平面ABCD，AB⊂平面ABCD，AD⊂平面ABCD，则PA⊥AB，PA⊥AD，又因四边形ABCD为矩形，则AB⊥AD.则阳马的外接球与以PA，AB，AD为长宽高的长方体的外接球相同.又PA=5，AB=3，AD=BC=4．则外接球的直径为长方体体对角线，故外接球半径为：R=PA 2+AB 2+AD 22=32+42+522=522，则外接球的表面积为：S =4πR 2=4π⋅504=50π.故选：B【反思】本例属于墙角型模型，通过补形，将原图形补成长方体模型，借助长方体模型求外接球半径.4(2023·全国·高三专题练习)已知菱形ABCD 的各边长为2,∠D =60°．如图所示，将ΔACD 沿AC 折起，使得点D 到达点S 的位置，连接SB ，得到三棱锥S -ABC ，此时SB =3．E 是线段SA 的中点，点F 在三棱锥S -ABC 的外接球上运动，且始终保持EF ⊥AC ，则点F 的轨迹的周长为()A.233π B.433π C.533π D.2213π【答案】C【详解】取AC 中点M ，则AC ⊥BM ,AC ⊥SM ,BM ∩SM =M ，∴AC ⊥平面SMB ，SM =MB =3，又SB =3，∴∠SBM =∠MSB =30°，作EH ⊥AC 于H ，设点F 轨迹所在平面为α，则平面α经过点H 且AC ⊥α，设三棱锥S -ABC 外接球的球心为O ,△SAC ,△BAC 的中心分别为O 1,O 2，易知OO 1⊥平面SAC ,OO 2⊥平面BAC ，且O ,O 1,O 2,M 四点共面，由题可得∠OMO 1=12∠O 1MO 2=60°，O 1M =13SM =33，解Rt △OO 1M ，得OO 1=3O 1M =1，又O 1S =23SM =233，则三棱锥S -ABC 外接球半径r =OO 21+O 1S 2=73，易知O 到平面α的距离d =MH =12，故平面α截外接球所得截面圆的半径为r 1=r 2-d 2=73-14=536，∴截面圆的周长为l =2πr 1=533π，即点F 轨迹的周长为533π．故选：C 【反思】此题典型的双面定球心。

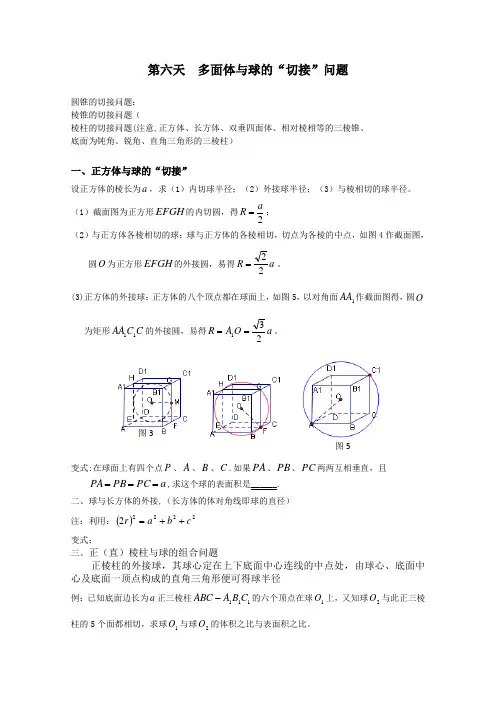
第六天 多面体与球的“切接”问题圆锥的切接问题：棱锥的切接问题（棱柱的切接问题(注意,正方体、长方体、双垂四面体、相对棱相等的三棱锥、底面为钝角、锐角、直角三角形的三棱柱）一、正方体与球的“切接”设正方体的棱长为a ，求（1）内切球半径；（2）外接球半径；（3）与棱相切的球半径。

（1）截面图为正方形EFGH 的内切圆，得2a R =； （2）与正方体各棱相切的球：球与正方体的各棱相切，切点为各棱的中点，如图4作截面图，圆O 为正方形EFGH 的外接圆，易得a R 22=。

(3)正方体的外接球：正方体的八个顶点都在球面上，如图5，以对角面1AA 作截面图得，圆O 为矩形C C AA 11的外接圆，易得a O A R 231==。

变式:在球面上有四个点P 、A 、B 、C .如果PA 、PB 、PC 两两互相垂直，且a PC PB PA ===,求这个球的表面积是______.二、球与长方体的外接,（长方体的体对角线即球的直径）注：利用：()22222c b a r ++= 变式：三、正（直）棱柱与球的组合问题正棱柱的外接球，其球心定在上下底面中心连线的中点处，由球心、底面中心及底面一顶点构成的直角三角形便可得球半径例：已知底面边长为a 正三棱柱111C B A ABC -的六个顶点在球1O 上，又知球2O 与此正三棱柱的5个面都相切，求球1O 与球2O 的体积之比与表面积之比。

图3 图4 图5分析：先画出过球心的截面图，再来探求半径之间的关系。

解：如图6，由题意得两球心1O 、2O 是重合的，过正三棱柱的一条侧棱1AA 和它们的球心作截面，设正三棱柱底面边长为a ，则a R 632=，正三棱柱的高为a R h 3322==，由O D A Rt 11∆中，得 22222221125633333a a a R a R =⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛=，a R 1251=∴ 1:5::222121==∴R R S S ，1:55:21=V V 四、 棱锥的内切、外接球问题例1：正四面体的外接球和内切球的半径是多少？分析：运用正四面体的二心合一性质，作出截面图，通过点、线、面关系解之。

1 / 5高考数学必备考试技能之“二级结论*提高速度”原创精品【2020版】结论九：多面体的外接球和内切球结 论 1.长方体的体对角线长d 与共顶点的三条棱的长a,b,c 之间的关系为d 2=a 2+b 2+c 2;若长方体外接球的半径为R,则有(2R)2=a 2+b 2+c 2.2.棱长为a 的正四面体内切球半径r=√612a,外接球半径R=√64a.解 读 通过选择最佳角度找出含有正棱锥特征元素的外接球的一个轴截面圆，于是该圆的半径就是所求的外接球的半径.从而把立体几何问题转化为平面几何问题来研究典例已知三棱锥S ABC -的所有顶点都在球O 的求面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =，则此棱锥的体积为（ ） A ．26B ．36C ．23D ．22解 析根据题意作出图形：设球心为O ，过ABC 三点的小圆的圆心为O 1，则OO 1⊥平面ABC ， 延长CO 1交球于点D ，则SD ⊥平面ABC ．∵CO 1=233323⨯=， ∴116133OO =-=，∴高SD=2OO 1=263，∵△ABC 是边长为1的正三角形，∴S △ABC =34， ∴132623436S ABC V -=⨯⨯=三棱锥．反 思本题考查棱锥与外接球问题，首先我们要熟记一些特殊的几何体与外接球（内切球）的关系，如正方体（长方体）的外接球（内切球）球心是对角线的交点，正棱锥的外接球（内切球）球心在棱锥的高上，对一般棱锥来讲，外接球球心到名顶点距离相等，当问题难以考虑时，可减少点的个数，如先考虑到三个顶点的距离相等的点是三角形的外心，球心一定在过此点与此平面垂直的直线上．如直角三2 / 5角形斜边中点到三顶点距离相等等等．针对训练*举一反三1．已知三棱锥O ABC -中，A ，B ，C 三点在以O 为球心的球面上，若2AB BC ==，120ABC ∠=︒，且三棱锥O ABC -的体积为3，则球O 的表面积为（ ） A ．323πB ．16πC ．52πD ．64π【答案】C【解析】由题意2AB BC ==，ABC 1120=||||sin 32ABC S AB BC ABC ∆∠=︒∠=， 1333O ABC ABC V S h h -∆==∴=.又ABC ∆的外接圆的半径222sin 2sin 30oAB r C ===因此球O 的半径222313R =+= 球的表面积：2452S R ππ==.故选：C2．点P 为棱长是2的正方体1111ABCD A B C D -的内切球O 球面上的动点，点M 为11B C 的中点，若满足DP BM ⊥，则动点P 的轨迹的长度为( )A ．55π B ．255πC ．455πD ．855π【答案】C【解析】根据题意,点P 为棱长是2的正方体1111ABCD A B C D -的内切球O 球面上的动点,点M 为11B C 的中点,设1BB 中点为N ,1AB 中点为K ,如下图所示:3 / 5在平面11BB C C 中,CN BM ⊥ 由题意可知DP BM ⊥,CN 为DP 在平面11BB C C 内的射影,所以直线DP 在过点D 且与BM 垂直的平面内又因为P 在正方体内切球的球面上所以点P 的轨迹为正方体的内切球与过D 且与BM 垂直的平面相交得到的小圆,即P 的轨迹为过,,D C N 的平面即为平面CDKN 与内切球的交线 因为,,D O N 位于平面11DD B B 内, 设O 到平面CDKN 的距离为h 所以由C DON O DCN V V --=,可得1111111322232ON DD AC CD CN h ⎛⎫⎛⎫⨯⨯⨯⨯=⨯⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭ 代入可得1111212253232h ⨯⨯⨯⨯=⨯⨯⨯⨯,解得55h = 正方体的内切球半径为1R =由圆的几何性质可得所截小圆的半径为2525155r ⎛⎫=-= ⎪ ⎪⎝⎭所以小圆的周长为4525C r ππ==即动点P 的轨迹的长度为455π，故选:C 3．长方体1111ABCD A B C D -各顶点都在球O 面上，1::1:1:2AB AD AA =，,A B 两点球面距离m ，A 、4 / 51D 两点球面距离n ，则mn值（ ） A ．33B ．3C ．12D ．2【答案】C【解析】如图所示：设AB a ，则AD a =，12AA a =⇒球的直径222222R a a a a =++=，即R a =， 则OAB 是等边三角形11263m a a ππ⇒=⋅=， 在1AOD 中，1OA OD a ==，13AD a =，1112023AOD n a π∠︒⇒=⋅= 故12m n =，故选：C . 4．已知球O 与棱长为2的正方体1111ABCD A B C D -的各面都相切，则平面1ACB 截球O 所得的截面圆与球心O 所构成的圆锥的体积为 （ ） A ．239π B ．318π C ．2327π D ．354π 【答案】C【解析】因为球O 与棱长为2的正方体1111ABCD A B C D -的各面都相切 所以球O 为正方体1111ABCD A B C D -的内切球，则球O 的半径1r =球心O 到A 的距离为22222232OA ++==底面1ACB 为等边三角形，所以球心O 到平面1ACB 的距离为()22233633d ⎛⎫=-⨯= ⎪⎝⎭5 / 5所以平面1ACB 截球O 所得的截面圆的半径为2236133⎛⎫-= ⎪ ⎪⎝⎭ 所以圆锥的体积为21632333327V ππ⎛⎫=⨯⨯⨯= ⎪ ⎪⎝⎭，所以选C 5．棱长为1的正方体1111ABCD A B C D -内有一个内切球O ，过正方体中两条互为异面直线的AB ，11A D 的中点,P Q 作直线，该直线被球面截在球内的线段的长为（ ） A ．22B ．12C ．24D ．21-【答案】A【解析】以D 为坐标原点建立空间直角坐标系,所以球心111,,222O ⎛⎫⎪⎝⎭,111,,0,,0,122P Q ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,62PQ =,22OP OQ ==,故O 到直线PQ 的距离为22262244⎛⎫⎛⎫-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,而球的半径为12,所以在球内的线段长度为221222242⎛⎫⎛⎫-= ⎪ ⎪ ⎪⎝⎭⎝⎭.故选A .。

常见多面体外接球的有关计算首先，我们需要了解外接球的定义。

给定一个多面体，外接球是一个球，可以和这个多面体的所有顶点都切线相切。

1.正方体外接球的计算：一个正方体的外接球半径等于边长的一半。

因此，可以通过给定的边长计算出外接球的半径。

2.正六面体外接球的计算：正六面体是一个六个等边三角形构成的多面体。

外接球半径等于正六面体边长的一半。

因此，可以通过给定的边长计算出外接球的半径。

3.正八面体外接球的计算：正八面体是一个八个等边三角形构成的多面体。

外接球半径等于正八面体边长的一半乘以根号2、因此，可以通过给定的边长计算出外接球的半径。

4.正十二面体外接球的计算：正十二面体是一个十二个等边五边形构成的多面体。

外接球半径等于正十二面体边长的一半乘以根号3、因此，可以通过给定的边长计算出外接球的半径。

5.正二十面体外接球的计算：正二十面体是一个二十个等边三角形构成的多面体。

外接球半径等于正二十面体边长的一半乘以根号3乘以根号(5+2√5)除以4、因此，可以通过给定的边长计算出外接球的半径。

对于体积的计算，可以使用外接球的半径和体积公式来计算。

体积公式为：V=(4/3)*π*r³，其中V代表体积，π代表圆周率，r代表外接球的半径。

对于表面积的计算，可以使用外接球的半径和表面积公式来计算。

表面积公式为：S=4*π*r²，其中S代表表面积，π代表圆周率，r代表外接球的半径。

以上是常见多面体外接球的计算方法。

通过这些计算，我们可以得到多面体的外接球的半径、体积和表面积等相关信息。

这些计算方法对于解决与多面体相关的问题和应用非常有用。

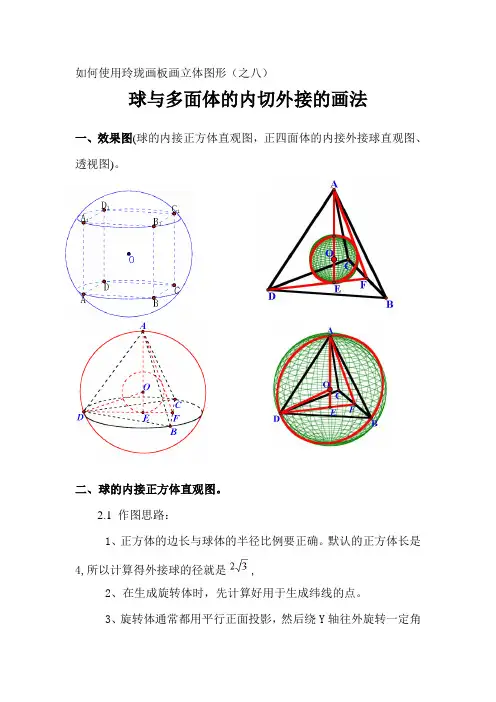
如何使用玲珑画板画立体图形（之八）球与多面体的内切外接的画法一、效果图(球的内接正方体直观图，正四面体的内接外接球直观图、透视图)。

二、球的内接正方体直观图。

2.1 作图思路：1、正方体的边长与球体的半径比例要正确。

默认的正方体长是4,所以计算得外接球的径就是,2、在生成旋转体时，先计算好用于生成纬线的点。

3、旋转体通常都用平行正面投影，然后绕Y轴往外旋转一定角度最佳。

4、为保持大圆为实线，所以外面的大圆不需旋转。

2.2右键菜单：2D网格模式，然后，画一半径为的半圆（为生成旋转体做准备），在屏幕中央画一点，然后再重合创建一点，选中这个点，单击菜单：编辑/精确定位/定值轴位移，输入2*sqrt(3)。

然后单击菜单：创建/圆/圆弧。

2.3然后在上下距圆心为2画两条线段与半圆相交。

为生成纬线点做准备。

然后在与圆弧交点处点击创建交点。

然后重合交点，新建自由点，2.4然后删除线段及端点，选中所有。

右键菜单：生成旋转体。

2.5单击菜单：创建/正多面体/正六面体，然后捕捉以球心，单击，则以球心为中心创建了一个正方体。

2.5选中所有，单击菜单：编辑/投影方式/平行正面投影，为效果方便，只选中正方体，通过操作轴，绕Z（绿色那个圈）旋转一点点。

2.6选中所有对象，右键菜单：合成组件。

2.7选中球的构成大圆的两个半圆弧，隐藏，以球心为圆心，球半径大小另画一个大圆：单击菜单：创建/圆/圆。

这里必须是自由圆。

2.8选中正方体与球的合成体（不选中大圆），通过操作轴绕Y(红色那个圈)，往外旋转一定角度。

2.9选中所有对象，合成组件。

注意：如果是做透视图效果的话，则从2.6合成组件后，就修改旋转体属性为网格显示即可。

三、正四面体的内切外接球直观图画法。

3.1作图思路：正四面体的高与球体的半径比例要正确。

计算比为：4：33.2右键菜单：2D网格模式。

单击菜单：创建/圆/圆弧，画出半径为3的半圆。

3.3然后在下距圆心为1画一条线段与半圆相交。