根的判别式与韦达定理专项

一元二次方程根的判别式及韦达定理常见题型及注意事项一、一元二次方程跟的判别式的常见题型 题型1：不解方程，判断一元二次方程根的情况.6232)3(;0123)2(;0345)1(222x x x x x x =+=++=--题型2：证明一元二次方程根的情况求证：无论k 取何实数，关于x 的一元二次方程：2(1)40x k x k -++-=总有两个不等实根。

题型3：已知一元二次方程根的情况．．，求方程中未知系数的取值范围 1．（ 2011·重庆）已知关于x 的一元二次方程．．．．．．(a －1)x 2－2x +1=0有两个不相等的．．．．．．实数根,则a 的取值范围是( )A.a <2 B,a >2 C.a <2且a ≠1 D.a <－2· 变式1：（2010·安徽芜湖）关于x 的方程．．(a －5)x 2－4x －1＝0有实数根．．．．，则a 满足（） A ．a ≥1 B ．a ＞1且a ≠5 C ．a ≥1且a ≠5 D ．a ≠5注意：要特别注意二次项系数是否为0，即原方程是否“一定为一元二次方程”。

变式2：（2010 ·成都）若关于x 的一元二次方程2420x x k ++=有两个实数根，求k 的取值范围及k 的非负整数．．．．值.变式3：已知关于x 的一元二次方程(12)10k x k x --=有两个实数根，求k 的取值范围二、一元二次方程根与系数的关系------韦达定理的常见题型 题型1：已知一元二次方程的一根，求另一根及未知系数k 的值 已知23-是方程210x kx ++=的一根，则方程的另一根是 ，k = 。

题型2：求与一元二次方程根有关的代数式的值； 1. 已知12,x x 是方程22430xx --=的两根，计算： （1）2212x x +； ⑵ 1211x x +；⑶212()x x -变式：已知,a b是方程2201230x x -+=的两实根，求22(20103)(20103)a a b b -+-+的值题型3：已知一元二次方程两根的关系．．．．．，求方程中未知系数的取值 1． 关于x 的一元二次方程22(21)10xk x k +-+-=的两个实根的平方和等于9，求k 的值变式1： （2011·荆州）关于x 的方程0)1(2)13(2=+++-a x a ax有两个不相等的实根1x 、2x ，且有a x x x x -=+-12211，则a 的值是（ ）A ．1B ．－1C ．1或－1D ． 2注意：要特别注意应用韦达定理的前提条件是原方程有实根，即原方程：△≥0。

专题复习二 根的判别式与韦达定理重点提示： (1)根的判别式ac b 42-主要应用于判断方程根的情况.利用判别式判断方程根的情况时要注意方程是不是一元二次方程，如果方程的类型不确定还要进行分类讨论.（2）韦达定理主要反映一元二次方程根与系数的关系，利用韦达定理的前提条件是方程有解，即042≥-ac b .【夯实基础巩固】1． 已知x 1，x 2是方程x 2+2x ﹣5=0的两根，则的值为（ B ）A ．﹣B ．C ．D ．﹣2．已知x 2+px +q =0的两根是3，﹣4，则代数式x 2+px +q 分解因式的结果是（ C ）A ． （x +3）（x +4）B ． （x ﹣3）（x ﹣4）C ． （x ﹣3）（x +4）D ． （x +3）（x ﹣4）3．关于x 的方程x 2﹣2mx ﹣m ﹣1=0的根的情况是（ A ）A ． 有两个不相等的实数根B ． 有两个相等的实数根C ． 有两个实数根D ． 没有实数根4．关于x 的方程x 2﹣（m ﹣1）x +m ﹣2=0的两根互为倒数，则m 的值是（ C ）A ． 1B ． 2C ． 3D ． 45．关于x 的方程x 2﹣（m ﹣3）x +m 2=0有两个不相等的实数根，则m 的最大整数值是（ B ）A ． 2B ． 1C ． 0D ． ﹣16．已知关于x 的一元二次方程x 2+kx +1=0有两个相等的实数根，则k = ±2 ．7．已知x 1，x 2是方程的两根，则的值为 3 ．8．已知a ，b 是一元二次方程x 2﹣2x ﹣1=0的两个实数根，则代数式（a ﹣b ）（a +b ﹣2）+ab 的值等于 ﹣1 ．9．已知关于x 的方程x 2+2mx +m 2﹣1=0.（1）不解方程，判别方程根的情况.（2）若方程有一个根为3，求m 的值．（1）∵∆=（2m ）2﹣4×1×（m 2﹣1）=4＞0，∴方程x 2+2mx +m 2﹣1=0有两个不相等的实数根.（2）∵x2+2mx+m2﹣1=0有一个根是3，∴32+2m×3+m2﹣1=0，解得m=﹣4或m=﹣2．10．已知关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根．（1）求实数m的最大整数值.（2）在（1）的条件下，方程的实数根是x1，x2，求代数式x12+x22﹣x1x2的值．（1）∵x2﹣2x+m=0有两个不相等的实数根，∴ =8﹣4m＞0，解得m＜2，∴m的最大整数值为1.（2）∵m=1，∴此一元二次方程为x2﹣2x+1=0.∴x1+x2=2，x1x2=1.∴x12+x22﹣x1x2=（x1+x2）2﹣3x1x2=8﹣3=5．【能力提升培优】11．若a，b，c为三角形三边，则关于x的一元二次方程x2+（a﹣b）x+c2=0的根的情况是（C）A．有两个相等的实数根B．有两个不相等的实数根C．没有实数根D．无法确定12．已知一元二次方程ax2+bx+c=0（a≠0），给出下列命题：①若a+b+c=0，则b2﹣4ac≥0；②若方程ax2+bx+c=0两根为﹣1和2，则2a+c=0；③若方程ax2+c=0有两个不相等的实根，则方程ax2+bx+c=0必有两个不相等的实根．其中真命题有（C）A．1个B．2个C．3个D．0个13．设x1，x2是关于x的方程x2+px+q=0的两根，x1+1，x2+1是关于x的方程x2+qx+p=0的两根，则p，q的值分别为（A）A．﹣1，﹣3 B．1，3 C．1，﹣3 D．﹣1，3【解析】∵x1，x2是x2＋px＋q=0的两根，x1＋1，x2＋1是x2＋qx＋p=0的两根，∴x1＋x2=-p，x1x2=q，x1＋1＋x2＋1= x1＋x2＋2=-q，（x1＋1）（x2＋1）= x1x2+（x1＋x2）＋1=p.∴-p+2=-q，q-p＋1=p.∴p=-1，q=-3.14．若一元二次方程x2﹣（a+2）x+2a=0的两个实数根分别是3，b，则a+b=5．15．已知m，n是方程x2﹣2x﹣1=0的两根，且（7m2﹣14m+a）（3n2﹣6n﹣7）=8，则a的值等于﹣9．16．已知关于x的方程x2﹣（a+b）x+ab﹣1=0，x1，x2是此方程的两个实数根，现给出三个结论：①x1≠x2；②x1x2＜ab；③．则正确结论的序号是①②．17．关于x的一元二次方程x2+（2k+1）x+k2+1=0有两个不等实根x1，x2．（1）求实数k的取值范围．（2）若方程两实根x1，x2满足|x1|+|x2|=x1x2，求k的值．（1）∵原方程有两个不相等的实数根，∴∆=（2k+1）2﹣4（k2+1）=4k2+4k+1﹣4k2﹣4=4k﹣3＞0，解得k＞.（2）∵k＞，∴x1+x2=﹣（2k+1）＜0.又∵x1x2=k2+1＞0，∴x1＜0，x2＜0.∴|x1|+|x2|=﹣x1﹣x2=﹣（x1+x2）=2k+1.∵|x1|+|x2|=x1x2，∴2k+1=k2+1.∴k1=0，k2=2.又∵k＞，∴k=2．18．设m是不小于﹣1的实数，关于x的方程x2+2（m﹣2）x+m2﹣3m+3=0有两个不相等的实数根x1，x2．（1）若+=1，求的值.（2）求+﹣m2的最大值．∵方程有两个不相等的实数根，∴∆= 4（m﹣2）2﹣4（m2﹣3m+3）=﹣4m+4＞0，解得m＜1.∴﹣1≤m＜1．（1）∵x1+x2=﹣2（m﹣2），x1x2=m2﹣3m+3，∴+===1，解得m1=，m2=（不合题意，舍去）.∴=﹣2．（2）+﹣m2=﹣m2=﹣2（m﹣1）﹣m2=﹣（m+1）2+3．当m=﹣1时，最大值为3．【中考实战演练】19．【烟台】等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根，则n的值为（B）A．9B．10 C．9或10 D．8或10【解析】∵a,b,2是等腰三角形的三边长，∴a=2,b＜4或a＜4，b=2或a=b＞1. ∵a,b是x2-6x+n-1=0的两根，∴a+b=6.∴a=b=3.∴ab=n-1=9.∴n=10.20．已知m，n是关于x的一元二次方程x2﹣2ax+a2+a﹣2=0的两实根，那么m+n的最大值是4．【开放应用探究】21．若x1，x2是关于x的方程x2+bx+c=0的两个实数根，且|x1|+|x2|=2|k|（k是整数），则称方程x2+bx+c=0为“偶系二次方程”．如方程x2﹣6x﹣27=0，x2﹣2x﹣8=0，x2+3x﹣=0，x2+6x ﹣27=0，x2+4x+4=0，都是“偶系二次方程”．（1）判断方程x2+x﹣12=0是否是“偶系二次方程”，并说明理由.（2）对于任意一个整数b，是否存在实数c，使得关于x的方程x2+bx+c=0是“偶系二次方程”？请说明理由．（1）不是.理由如下：解方程x2+x﹣12=0得x1=3，x2=﹣4．∴|x1|+|x2|=3+4=7=2×3.5．∵3.5不是整数，∴x2+x﹣12=0不是“偶系二次方程.（2）存在．理由如下：∵x2﹣6x﹣27=0和x2+6x﹣27=0是偶系二次方程，∴假设c=mb2+n.当b=﹣6，c=﹣27时，﹣27=36m+n．∵x2=0是偶系二次方程，∴n=0，m=﹣.∴c=﹣b2．∴可设c=﹣b2．对于任意一个整数b，c=﹣b2时， =b2﹣4c=4b2．∴x1=﹣b，x2=b．∴|x1|+|x2|=2|b|，∵b是整数，∴对于任何一个整数b，当c=﹣b2时，关于x的方程x2+bx+c=0是“偶系二次方程”．。

八年级数学竞赛专题训练试卷(三)一元二次方程根的判别式与韦达定理一、选择题(每小题4分，共40分)1．若m ，n 是二次方程x 2+1994x+7=0的两根，那么(m 2+1993m+6)(n 2+1995n+8)等于( )(A)2000 (B)1994 (C)1986 (D)72．若a b ≠1，且有5a 2+2001a+9=0及9b 2+2001b+5=0，则b a的值是 ( ) (A)95 (B)59 (C)20015- (D)20019- 3．已知一元二次方程px 2－qx －p=0有两根a 和b ，则以1a 和1b 为根的一元二次方程是 ( )(A)px 2+qx －p =0 (B)px 2+qx+p=0(C)qx 2+px －q=0 (D)qx 2+px+q=04．已知3m 2－2m －5=0，5n 2+2n －3=0，其中m ，n 为实数，则1m n-= ( ) (A)0 (B)83 (C)53 (D)0或835．方程x 2+px+1997=0有两个正整数根x 1，x 2，则()()1211px x ++= ( )(A)1 (B)－1 (C)－0．5 (D)12 6．两个质数a ，b 恰好是整系数方程x 2－99x+m=0的两个根，则b a a b+的值为 ( ) (A)9413 (B)9413194 (C)941399 (D)9413977．设x 1，x 2是二次方程x 2+x －3=0的两个根，那么3212419x x -+的值等于 ( )(A)－4 (B)8 (C)6 (D)08．若方程8x 2－(m －1)x+(m －7)=0有一个正根，一个负根，则 ( )(A) m ＞7 (B) m ＞1 (C) m ＜1 (D) m ＜79．设关于x 的方程ax 2 +(a+2)x+9a=0有两个不相等的实数根x 1，x 2且x 1＜1＜x 2，那么a 的取值范围是 ( )(A)2275a -<< (B)25a > (C)27a <- (D)2011a -<< 10．已知方程ax 2+bx+c=0的两实根是a ，c(ac ≠0)，则方程9cx 2+3bx+a=0的根的情况是( )(A)必有一根为13 (B)必有一根为19(C)两根分别为13，13- (D)必有一根为13或13- 二、填空题(每小题4分，共40分)11．关于x 的一元二次方程x 2－x+a(1－a)=0有两个不相等的正根，则a 可取值为_________ (只要填写一个可能的数值即可)．12．当m________时，关于x 的方程4x 2－(m 2－m －2)x －m=0的两根互为相反数．13．已知x ，y 满足x 2－7x+1=0，y 2－7y+1=0，则y x x y+=_________． 14．已知方程x 2－x －4=0的两根为x 1，x 2，则x 1 +x 2=________，2112224x x x x -+-=______． 15．已知菱形ABCD 的边长是5，对角线AC 与BD 交于点O ，且AO ，BO 的长分别是关于x 的方程x 2 +(2m －1)x+m 2 +3=0的根，则m 的值为________．16．已知关于x 的一元二次方程ax 2 +bx+c=0没有实数根，甲由于看错了二次项的系数误求得两根为2和4；乙由于看错了某一项的系数的符号，误求得两根为－1和4，那么23b c a+的值为_______． 17．方程(2002x) 2－2001×2003x －1=0的较大根为a ，x 2 +2002x －2003=0的较小根为b ，则a 2－b=_________．18．已知二次方程(ab －2b)x 2 +2(b －a)x+2x －ab=0有两个相等的实数根，那么11a b+=____． 19．已知实数a ，b ，c 满足a+b+c=0，a 2 +b 2 +c 2=6，则a 的最大值为_________．20．若α，β为x 2 +2x －5=0的两根，则22ααβα++的值为__________．三、解答题(21题满分10分，22题、23题每题满分15分，共40分)21．已知方程a(2x+a)=x(1－x)的两实数根为x 1，x 2，设S =(1)当a=－2时，求S 的值．(2)当a 取什么整数时，S 的值为1 ?(3)是否存在负数a ，使S 2的值不小于25 ?若存在，请指出a 的取值范围，若不存在，请说明理由．22．已知方程x 2 +(m+1)x+2m －1=0的两根都是整数，求m 的整数值．23．已知实数a，b，c满足a+b+2c=1，223602a b c+++=，求a，b，c的值．参考答案一、选择题1．C 2．A 3．A 4．D 5．C 6．B 7．D 8．D ． 9．D 10．D二、填空题11．12a ≠即可． 12．m=2． 13．2或47． 14．1，5． 15．m=－3． 16．6 17．2004． 18．1 19．2． 20．0．三、解答题21．(1)由题意易求得S=3．(2) a 取0时，S=1．(3)存在负数a ，使S 2≥25．因212225S a a =-+≥且a ＜0，所以l －4a ≥25，则a ≤－6．22．m=5或m=3．23．32a b ==，c=－1．。

根的判别式ac b 42-根的判别式的作用：①判定根的个数；②求待定系数的值；③应用于其它。

例1、若关于x 的方程0122=-+x k x 有两个不相等的实数根，则k 的取值范围是 。

例2、已知方程022=+-mx mx 有两个不相等的实数根，则m 的值是 . 例3、关于x 的方程()0212=++-m mx x m 有实数根，则m 的取值范围是( )A.10≠≥且m mB.0≥mC.1≠mD.1>m例4、已知关于x 的方程()0222=++-k x k x(1)求证：无论k 取何值时，方程总有实数根；(2)若等腰∆ABC 的一边长为1，另两边长恰好是方程的两个根，求∆ABC 的周长。

例5、已知二次三项式2)6(92-++-m x m x 是一个完全平方式，试求m 的值.例6、已知关于x 的方程0k x 4k 2x 2=++-有两个不相等的实数根，（1）求k 的取值范围。

（2）化简4k 4k 2k 2+-+--针对练习：1、当k 时，关于x 的二次三项式92++kx x 是完全平方式。

2、当k 取何值时，多项式k x x 2432+-是一个完全平方式？这个完全平方式是什么？3.关于x 的方程(a －5)x 2－4x －1＝0有实数根，则a 满足（ ）A ．a ≥1B ．a ＞1且a ≠5C ．a ≥1且a ≠5D ．a ≠54．对任意实数m ，求证：关于x 的方程042)1(222=++-+m mx x m 无实数根.5．k 为何值时，方程0)3()32()1(2=+++--k x k x k 有实数根.6. 已知a 、b 、c 是ABC ∆三条边的长，那么方程()042=+++c x b a cx 的根的情况是考点五、方程类问题中的“分类讨论”典型例题：例1、关于x 的方程()03212=-++mx x m⑴有两个实数根，则m 为 ,⑵只有一个根，则m 为 。

例2、如果关于x 的方程022=++kx x 及方程022=--k x x 均有实数根，问这两方程是否有相同的根？若有，请求出这相同的根及k 的值；若没有，请说明理由。

《一元二次方程根的判别式和根与韦达定理》 同步练习一、填空题和选择题1、（泸州）设12,x x 是方程2330x x +-=的两个实数根，则2112x x x x +的值为 A.5 B.-5 C.1 D.-12、（眉山）已知关于x 的一元二次方程032=--x x 的两个实数根分别为α、β，则(α+3)(β+3)=______3、（2牡丹江）若关于x 的一元二次方程为ax 2+bx+5=0（a ≠0）的解是x=1，则2013﹣a ﹣b 的值是（ ）A ．2018B ． 2008C ． 2014D ． 20124. （2012湖北襄阳）如果关于x 的一元二次方程2kx 2k 1x 10-++=有两个不相等的实数根，那么k 的取值范围是【 】A ．k ＜12B ．k ＜12且k ≠0C ．﹣12≤k ＜12D ．﹣12≤k ＜12且k ≠05、（2013•自贡）已知关于x 的方程x 2﹣（a+b ）x+ab ﹣1=0，x 1、x 2是此方程的两个实数根，现给出三个结论：①x 1≠x 2；②x 1x 2＜ab ；③．则正确结论的序号是 ．（填上你认为正确结论的所有序号） 二、解答题1．设关于x 的方程kx 2－(2k ＋1)x ＋k ＝0的两实数根为x 1、x 2，，若,4171221=+x x x x 求k 的值.2、（2013• 日照）已知，关于x 的方程x 2－2mx = －m 2＋2x 的两个实数根1x 、2x 满足12x x =，求实数m 的值.3、（2013•孝感）已知关于x 的一元二次方程x 2﹣（2k+1）x+k 2+2k=0有两个实数根x 1，x 2．（1）求实数k 的取值范围；（2）是否存在实数k 使得≥0成立？若存在，请求出k 的值；若不存在，请说明理由．4、（2013•荆州）已知：关于x的方程kx2－(3k－1)x+2(k－1)=0（1）求证：无论k为何实数，方程总有实数根；（2）若此方程有两个实数根x1，x2,且│x1－x2│=2,求k的值.5. (2010．十堰)已知关于x的方程mx2-(3m－1)x+2m－2=0（1）求证：无论m取任何实数时，方程恒有实数根.（2）若关于x的二次函数y= mx2-(3m－1)x+2m－2的图象与x轴两交点间的距离为2时，求抛物线的解析式.6、如图，平行四边形 ABCD中，两条对角线交于O点，且AO、BO的长分别是关于x的方程3)12(22=++-+mxmx的根。

一元二次方程根的判别式练习题1.若关于x 的一元二次方程2340mx x +-=有实数根，则m 的值为____．2.若一元二次方程213)420k x x --=（＋有实数根，则k 的取值范围是____． 3.若关于x 的二次方程221kx x x +=-有实数根，则k 的取值范围是____． 4.如果关于x 的一元二次方程2()2460x ax x +=－－没有实数根，那么a 的最小整数值是 。

5.若m 是非负整数且一元二次方程22121)10)m x m x -+--=（（有两个实数根，则m 的值为____．6.二次方程221631720k x k x ---+=（)（)有两个实数根，则k 为___． 7.方程220x x m ++=有两个相等实数根，则m= 。

8.若方程221210a x bx c x -=（)＋＋（＋）的两个实数根相等，则a ，b ，c 的关系式为_____．9.当m 时，关于x 的方程3x 2－2(3m+1)x+3m 2－1=0有两个不相等的实数根。

10.关于x 的一元二次方程22()3231310x m x m ++=－－的根的判别式的值等于4，则m= 。

11.关于x 的方程()22110kx k x k +++=－的实根的情况是 。

12.关于x 的方程()()2221240k x kx k +++=－的根的情况是 。

13.当k ＜1时，方程2214210k x kx k ++-=（)＋有____实数根． 14.方程222393440x x x x ++=（＋）（)＋解的情况是＿解． 15.求证：关于x 的方程()()2221240m x mx m +++=－没有实数根。

16.已知关于x 的方程220x x m =－－无实根(m 为实数)，证明关于x 的方程()222212110()x mx m x ++++=－也无实根。

17.m 为何值时，方程()2214210m x mx m +++=－。

第十讲：一元二次方程实数根与韦达定理（初中衔接）一、知识要点实系数一元二次方程:()200ax bx c a ++=≠的两个根为12,x x ，1.根的判别式24b ac ∆=-：当0∆<时,方程没有实根；当0∆=时,时,有两个不相等的实根。

2.韦达定理重要公式 二、例题分析例1.已知方程220x x m --=()m R ∈没有实根,试判断关于x 的方程 221x mx +++()()222110m x -+=有无实根。

例2．（1）已知12,x x 是方程22310x x --=的根，求22332112121222121211,,,,x x x x x x x x x x x x ++++-的值；练习：如果,a b 是方程012=-+x x 的两个根，那么代数式3223b ab b a a +++的值是 。

（2）若方程2(32)0x x a +--=的两实根均小于1，求实数a 的取值范围；（3）已知方程01532=+-x x ，求解新方程使它的根是原方程根的平方；（4）已知方程0252=-+x x ，作一个新的一元二次方程,使它的根分别是已知方程各根的平方的倒数；练习：已知方程25230x x +-=求作一个方程，使它的根是原方程根的负倒数。

（5）已知抛物线21244y mx mx m =-+与x 轴的两个交点的坐标为12(,0),(,0)A x B x （12x x <），且221234x x +=。

①求12,,m x x 的值；②在抛物线上是否存在点C ，使ABC ∆是一个顶角为0120的等腰三角形?若存在，请求出所有点C 的坐标；若不存在，请说明理由。

例3.设关于x 的方程:()()2222134420x a x a ab b ++++++=有实根,求实数,a b 的值。

例4.已知,m k 为有理数，当k 为何值时，方程22443240x mx x m m k -++-+=有有理根？例5.已知,x y 均为实数,且满足221x y x x =++，求y 的最大值和最小值。

第4周 根的判别式与韦达定理例1、若关于x 的方程0122=-+x k x 有两个不相等的实数根，则k 的取值范围是 。

例2、关于x 的方程()0212=++-m mx x m 有实数根，则m 的取值范围是( )A.10≠≥且m mB.0≥mC.1≠mD.1>m例3、已知关于x 的方程()0222=++-k x k x(1)求证：无论k 取何值时，方程总有实数根；(2)若等腰∆ABC 的一边长为1，另两边长恰好是方程的两个根，求∆ABC 的周长。

例4、已知二次三项式2)6(92-++-m x m x 是一个完全平方式，试求m 的值.说明：若二次三项式为一个完全平方式，则其相应方程的判别式0=∆即：若042=-ac b ，则二次三项式c bx ax ++2)0(≠a 为完全平方式；反之，若c bx ax ++2)0(≠a 为完全平方式，则042=-ac b .例5、m 为何值时，方程组⎩⎨⎧=+=+.3,6222y mx y x有两个不同的实数解？有两个相同的实数解？k 时，关于x 的二次三项式92++kx x 是完全平方式。

★2、当k 取何值时，多项式k x x 2432+-是一个完全平方式？这个完全平方式是什么？ ★3、已知方程022=+-mx mx 有两个不相等的实数根，则m 的值是 .★★4、k 为何值时，方程组⎩⎨⎧=+--+=.0124,22y x y kx y★★★5、当k 取何值时，方程（1）有两组相等的实数解，并求此解； 04234422=+-++-k m m x mx x （2）有两组不相等的实数解； 的根与m 均为有理数？（3）没有实数解.一、填空题：1、下列方程①012=+x ；②02=+x x ；③012=-+x x ；④02=-x x 中，无实根的方程是 。

2、已知关于x 的方程022=+-mx x 有两个相等的实数根，那么m 的值是 。

3、如果二次三项式k x x 2432+-在实数范围内总能分解成两个一次因式的积，则k 的取值范围是 。

x 2 - 2 |x |-15 = ( )A. 0B. - 2C. 2D. 8 【解答】解：①当 x > 0 时，方程化为： x 2 - 2x - 15 = 0， 即 (x + 3) (x - 5) = 0， ∴ x + 3 = 0，x - 5 = 0， 解得 x 1 = -3( 舍去 )，x 2 = 5，②当 x < 0 时，方程化为： x 2 + 2x - 15 = 0， 即 (x - 3) (x + 5) = 0， ∴ x - 3 = 0，x + 5 = 0， 解得 x 3 = 3( 舍去 )，x 4 = -5，③当 x = 0 时，方程不成立．∴ 此方程的所有实数根的和为： 5 + (-5) = 0．或原方程可化为： (|x |-5) (|x |+3) = 0， 即 |x |-5 = 0，|x |+3 = 0， ∴ |x | = 5，|x | = -3( 舍去 )， 解得 x = 5 或 -5，∴ 此方程的所有实数根的和为： 5 + (-5) = 0．故选：A ．x x 2 + (2m + 1)x + m 2 - 1 =(1(2【解答】解： (1) ∵ 关于 x 的一元二次方程 x 2 + (2m + 1)x + m 2 - 1 = 0 有两个不相等的实数根， ∴ b 2 - 4ac = (2m + 1)2 - 4(m 2 - 1) = 4m + 5 > 0，解得：m > - ，即 m 的取值范围是 m > - ；(2) 由 (1) 知：当 m > - 时，方程有两个不相等的实数根，∵ m 为不大于 1 的整数， ∴ m = 0，-1，1，又m = 0 时，方程北2+ 北 - 1 = 0 的根不是整数，当m = -1 时，则方程为北2- 北 = 0，解得：北1=1，北2=0，即当m = -1 时，方程的解是北1= 1，北2= 0．当m = 1 时，则方程为北2+ 3北 = 0，解得：北1= -3，北2= 0，即当m = 1 时，方程的解是北1= -3，北2= 0．(北 - 3)2 + (y - 3)2 =(北yy北【解答】解：设y= k北，则直线y= k北与圆 (北 - 3)2 + (y - 3)2 = 6 相切时k有最大值和最小值，把y = k北代入 (北 - 3)2 + (y - 3)2 = 6，得 (1 + k2)北2 - 6(k + 1)北 + 12 = 0，∴ Δ= 36(k + 1)2 - 4 × 12 × (1 + k2) = 0，即k2 - 6k + 1 = 0，解此方程得，k = 3 + 2 2 或3 - 2 2．所以y北= k 的最大值是3+ 2 2．北2北(北≥ 0)解：北2北28 = 2北 4 = 2(北 2 +北 2 ，因为北≥ 0，所以北 + 2 的最小值是2，所以北 2 的最大值是2，所以2 + 北 2 的最大值是4，即北2北 (北≥ 0) 的最大值是4．2北北【解答】解：2北北22210= 2北北2 6 = 2(北北2= 2 + 北2 2，∵ 北2≥ 0，∴北2 + 2 的最小值为2，∴北2 2的最大值为3，∴2 + 北2 2的最大值为5，∴分式2北北的最大值是5，故答案为：5．x(m - 4)x 2 + (2m - 1)x +1 = 0 s s【解答】解：根据题意得 m - 4 ≠ 0 且 Δ = (2m - 1)2 - 4(m - 4) ≥ 0，解得 m ≠ 4， x 1 + x 2 = - ，x 1x 2 =，s =+== -2m + 1，由于 m ≠ 4， 所以 s ≠ -7． 故答案为 s ≠ -7．x2x 2 - 4mx + 2m 2 + 3m - 2 = 0(1)m(2) x 1x 2mx 12+ x 22【解答】解： (1) ∵ 一元二次方程 2x 2 - 4mx + 2m 2 + 3m - 2 = 0 有两个实数根， ∴ b 2 - 4ac = (-4m )2 - 4 × 2(2m 2 + 3m - 2) ≥ 0， ∴ -24m + 16 ≥ 0， ∴ m ≤ ，∴ 实数 m 的取值范围为≤ ；(2) ∵ x 1 + x 2 = 2m ，x 1 •x 2 = (2m 2 + 3m - 2)，∴ x 12+ x 22= (x 1 + x 2)2 - 2x 1x 2 = (2m )2 - 2 × (2m 2 + 3m - 2) = 2m 2 - 3m + 2 = 2(m - 2+， ∵ m ≤ ， < ，∴ 当 m = 时，x + x 12 22= 2(- 2+ = ，∴ 当 m = 时，x 12+ x 22有最小值，最小值是 ．1.(x - 1) (x 2 - 2x + m ) =0m()A. 0 ≤ m ≤ 1B. ≤ mC. ≤ m ≤ 1D. < m ≤ 1【解答】解：∵ 方程(x- 1) (x2 - 2x+m) =0 有三根，∴ x1 = 1，x2 - 2x+m= 0 有根，方程x2 - 2x+m= 0 的Δ = 4 - 4m≥0，得m≤ 1．又∵ 原方程有三根，且为三角形的三边和长．∴ 有x2 + x3 > x1 = 1，|x2 - x3 | < x1 = 1，而x2 + x3 = 2 > 1 已成立；当|x2 - x3 | < 1 时，两边平方得：(x2 + x3)2 - 4x2x3 < 1．即：4 - 4m<1．解得m>．∴ <m≤ 1．故选：D．x(k- 1)2x2 + (2k+ 1)x+1 =k( )A. k> k ≠ 1B. k≥ k≠ 1C. k >D. k ≥【解答】解：当k - 1 ≠ 0，即k≠ 1 时，此方程为一元二次方程．∵ 关于x的方程(k- 1)2x2 + (2k+ 1)x+1 = 0 有实数根，∴Δ = (2k+ 1)2- 4 × (k- 1)2× 1 = 12k- 3 ≥ 0，解得k≥；当k- 1 = 0，即k= 1 时，方程为3x+1 = 0，显然有解；综上，k的取值范围是k≥，故选：D．3. m n x2 - 5x+ 1 = 0 S1= + S2= + ⋯St = + (t)S1 + S2 +⋯ S t= t2 - 56t( )A. 7B. 8C. 9D. 10【解答】解：∵ m，n是方程x2 - 5x+ 1 = 0 的两个根，∴m+n= 5，mn= 1，∴S1 = +1 + m+ 1 + n=(1 +m) (1 +n)2 + (m+ n)1+m+n+mn2 + 51 + 1 + 5= 1==，解得 - 3 < a < 1 2 2 ．1 + m2 1 + n 2 S 2 = +1 + m2 + 1 + n 2 =(1 + m 2) (1 + n 2) 2 + (m + n )2 - 2mn =1 + (m + n )2 - 2mn + (mn )22 + 5 - 21 + 5 -2 + 1= 1 …， ∴ S t =+= 1，∴ S 1 + S 2 +… S t = t 2 - 56， 1 + 1 +… +1 = t 2 - 56， t = t 2 - 56， t 2 - t - 56 = 0， (t - 8) (t + 7) = 0，解得： t = 8 或 t = -7( 舍去 )． 故选：B ．4.xx 2 - 2mx - 4m +1 = 0 (m - 2)2 - 2m (m - 1)【解答】解：由题意可知： Δ = 4m 2 - 2(1 - 4m ) = 4m 2 + 8m - 2 = 0， ∴ m 2 + 2m = ，∴ (m - 2)2 - 2m (m - 1) = -m 2 - 2m + 4 = - + 4= 7 2 ，故答案为： x 2 + 4ax - 4a + 3 = 0x 2 + (a - 1)x + 1 + a 2 = 0x 2 + 2ax - 2a + 3 = 0a(16a 2 + 16a - 12 < 0【解答】解：不妨假设三个方程都没有实数根，则有〈(a - 1)2 - 4(a 2 + 1) < 0 ，(4a 2 - 4(3 - 2a ) < 01 1=，故答案为：a≤ - 或a≥．6. x (1 - 2k )x2 - 2x - 1 = 0 k【解答】解：∵ 关于x的一元二次方程 (1 - 2k)x2 - 2x- 1 = 0 有两个不相等的实数根，(1 - 2k≠ 0∴〈k+ 3 ≥ 0 ，( △ = (-2)2 - 4(1 - 2k) × (-1) > 0解得： -3 ≤ k<4 且k≠ 1x x2 + ax- 1 = (x+ 1)2 + a(x+ 1) - 1 =【解答】解：∵ 关于x的一元二次方程x2 + ax- 1 = 0 的两个根分别为m、n，∴ m2 + am- 1 = 0，n2 + an- 1 = 0，设x+ 1 =m或n，则 (x+ 1)2 + a(x+ 1) - 1 = 0，∴ (x+ 1)2 + a(x+ 1) - 1 = 0 的根为x= m- 1 或n- 1，故答案为：x= m- 1 或n- 1．8. x y(2x+ 1)2 + y2 + (y- 2x)2 = x+ y【解答】解：由 (2x+ 1)2 + y2 + (y- 2x)2 = ，得(3x+ 1)2 + 3(x- y)2 = 0，则〈( x= -解得〈，故x+ y= - - = - ．x(a+ b)x2 + 2cx+ (b- a) =a b c△ABC(1x= -△ABC(2△ABC(3△ABC【解答】解： (1)△ABC是等腰三角形，理由：当x= -1 时，(a+ b) - 2c+ (b- a) = 0，2．故答案为： -3 ≤ k<4 且k≠．( y= - 312 ∴ b = c ，∴ △ABC 是等腰三角形，(2)△ABC 是直角三角形，理由： ∵ 方程有两个相等的实数根， ∴ Δ = (2c )2 - 4(a + b ) (b - a ) = 0， ∴ a 2 + c 2 = b 2，∴ △ABC 是直角三角形；(3) ∵ △ABC 是等边三角形， ∴ a = b = c ，∴ 原方程可化为： 2ax 2 + 2ax = 0， 即：x 2 + x = 0， ∴ x (x + 1) = 0， ∴ x 1 = 0，x 2 = -1，即：这个一元二次方程的根为 x 1 = 0，x 2 = -1．10.xax 2 + bx + c = 02t2tax 2 + bx + c = a (x - t ) (x - 2t ) = ax 2 - 3atx + 2t 2a b 2 - ac = 0K =b 2 - acK = 0 ax 2 + bx + c = 0 (1x 2 - x - 2 = x 2 - 6x +8 = )(2(x - 2) (mx + n ) =4m 2 + 5mn + n(3) xx 2 -x + n = 0(m ≥ 0)A (m n )y =3x - 8【解答】解： (1) 在方程①x 2 - x - 2 = 0 中，K = (-1)2 - × 1 × (-2) = 10 ≠ 0；在方程② x 2 - 6x + 8 = 0 中，K = (-6)2 - × 1 × 8 = 0． ∴ 是倍根方程的是②x 2 - 6x + 8 = 0．故答案为：②．(2) 整理 (x - 2) (mx + n ) =0 得：mx 2 + (n - 2m )x - 2n = 0， ∵ (x - 2) (mx + n ) =0 是倍根方程， ∴ K = (n - 2m )2 - 9 m • (-2n ) = 0，∴ 4m2 + 5mn+n2 = 0．(3) ∵ x2 - x+ n= 0 是倍根方程，∴ K= (-)2 - × n= 0，整理得：m= 3n．∵ A(m，n) 在一次函数y= 3x- 8 的图象上，∴n= 3m- 8，∴n= 1，m= 3，∴ 此方程的表达式为x2 - 3x+ = 0．11. m-1 x x2 + 2(m - 2)x+ m2 - 3m+3 = 0x1x2(1) x2+ x22= 6m1(2) +【解答】解：∵ 方程有两个不相等的实数根，∴ Δ = b2 - 4ac= 4(m- 2)2 - 4(m2 - 3m+ 3) = -4m+ 4 > 0，∴m< 1，结合题意知： -1 ≤ m< 1．(1) ∵ x2+ x22= (x1 + x2)2 - 2x1x2 = 4(m- 2)2 - 2(m2 - 3m+ 3) = 2m2 - 10m+ 10 = 61∴ m= ，∵ -1 ≤ m< 1，∴ m= ；(2) + = == = 2(m2 - 3m+ 1) = 2(m- 2 - (-1 ≤ m< 1)．∵对称轴m= ，2 > 0，∴当m= -1 时，式子取最大值为10．12. x2 + px+ q= 0 x1x2x1 + x2 = -p x1 •x2 = q(1) p= -4q= 3x2 + px+ q= 0则 x 1 + x 2 = x 1x 2 = - n ，x 1 • x 2 = x 1x 2 = n ，(2) a b a 2 - 15a - 5 = 0b 2 - 15b - 5 = 0 +(3x x 2 + mx + n = 0(n ≠ 0【解答】解： (1) 当 p = -4，q = 3，则方程为 x 2 - 4x + 3 = 0，解得： x 1 = 3，x 2 = 1．(2) ∵ a 、b 满足 a 2 - 15a - 5 = 0，b 2 - 15b - 5 = 0， ∴ a 、b 是x 2 - 15x - 5 = 0 的解， 当 a ≠ b 时，a + b = 15，ab = -5， + ==== -47；当 a = b 时，原式 = 2．(3) 设方程 x 2 + mx + n = 0，(n ≠ 0)，的两个根分别是 x 1，x 2， 1 1 x 1 + x 2 m 1 1 1 1 则方程 x 2 + x + = 0 的两个根分别是已知方程两根的倒数．以上就是韦达定理与根的判别式的全部内容~。

一、解一元二次方程1、()()513+=-x x x x2、x x 5322=- 3、2260x y -+= 4、01072=+-x x 5、()()623=+-x x 6、()()03342=-+-x x x 二、根的判别式练习题三、根与系数的关系（韦达定理）1、如果方程)0(02≠=++a c bx ax 的两根是1x 、2x ，那么21x x += ，21x x ⋅= 。

2、已知1x 、2x 是方程04322=-+x x 的两个根，那么：21x x += ；21x x ⋅= ；=+2111x x ；=+2221x x ；=++)1)(1(21x x ；||21x x -= 。

3、以2和3为根的一元二次方程(二次项系数为1)是 。

4、如果关于x 的一元二次方程022=++a x x 的一个根是1－2，那么另一个根是 ，a 的值为 。

5、如果关于x 的方程x 2+6x+k=0的两根差为2，那么k= 。

6、已知方程2x 2+mx －4=0两根的绝对值相等，则m= 。

7、一元二次方程px 2+qx+r=0(p ≠0)的两根为0和－1，则q ∶p= 。

8、已知方程x 2－mx+2=0的两根互为相反数，则m= 。

9、已知关于x 的一元二次方程(a 2－1)x 2－(a+1)x+1=0两根互为倒数，则a = 。

10、已知关于x 的一元二次方程mx 2－4x －6=0的两根为x 1和x 2，且21x x +=－2，则m= ，21x x ⋅ = 。

11、已知方程3x 2+x －1=0，要使方程两根的平方和为913，那么常数项应改为 。

12、已知二次项系数为1的一元二次方程，它的两根之和为5，两根之积为6，则这个方程为 。

13、若α、β为实数且｜α+β－3｜+(2－αβ)2=0，则以α、β为根的一元二次方程为 。

(其中二次项系数为1)14、已知关于x 的一元二次方程x 2－2(m －1)x+m 2=0。

若方程的两根互为倒数，则m= ；若方程两根之和与两根积互为相反数，则m= 。

一、概念习题1、方程782=x 的一次项系数是 ，常数项是 。

2、若方程()021=--m x m 是关于x 的一元一次方程，⑴求m 的值；⑵写出关于x 的一元一次方程。

3、若方程()112=•+-x m x m 是关于x 的一元二次方程，则m 的取值范围是 。

4、若方程nx m +x n -2x 2=0是一元二次方程，则下列不可能的是（ ）A.m=n=2B.m=2,n=1C.n=2,m=1D.m=n=15、方程()0132=+++mx x m m是关于x 的一元二次方程，则m 的值为 。

6、已知322-+y y 的值为2，则1242++y y 的值为 。

7、关于x 的一元二次方程()04222=-++-a x x a 的一个根为0，则a 的值为 。

8、已知关于x 的一元二次方程()002≠=++a c bx ax 的系数满足b c a =+，则此方程必有一根为 。

9、已知b a ,是方程042=+-m x x 的两个根，c b ,是方程0582=+-m y y 的两个根，则m 的值为 。

10、已知方程0102=-+kx x 的一根是2，则k 为 ，另一根是 。

11、已知关于x 的方程022=-+kx x 的一个解与方程311=-+x x 的解相同。

⑴求k 的值 ⑵方程另一个解。

12、已知m 是方程012=--x x 的一个根，则代数式=-m m 2。

13、已知a 是0132=+-x x 的根，则=-a a 622。

14、方程()()02=-+-+-a c x c b x b a 的一个根为（ ） A 1- B 1 C c b - D a -15、若=•=-+yx 则y x 324,0352 。

二、解法习题直接开平方法1、解关于x 的方程：();08212=-x ()216252x -=0; ()();09132=--x （4）02=-b ax2、若()()2221619+=-x x ，则x 的值为 。

一元二次方程两种关系【知识点1 一元二次方程根的判别式】一元二次方程根的判别式：∆=b2−4ac．①当∆=b2−4ac>0时，原方程有两个不等的实数根；②当∆=b2−4ac=0时，原方程有两个相等的实数根；③当∆=b2−4ac<0时，原方程没有实数根.【例1】下列关于x的方程有两个不相等的实数根的是（）A．x2﹣2x+2＝0 B．x（x﹣2）＝﹣1 C．（x﹣k）（x+k）＝2x+1 D．x2+1＝0 【变式1】关于x的一元二次方程x2+（﹣k+2）x﹣4+k＝0根的情况，下列说法正确的是（）A．有两个不相等的实数根 B．有两个相等的实数根 C．无实数根 D．无法确定【变式2】函数y＝kx+b的图象如图所示，则关于x的一元二次方程x2+bx+k﹣1＝0的根的情况是（）A．没有实数根 B．有两个相等的实数根 C．有两个不相等的实数根 D．无法确定【变式3】已知a，b，c分别是△ABC的边长，则一元二次方程（a+b）x2+2cx+a+b＝0的根的情况是（）A．没有实数根 B．有两个相等的实数根C．有两个不相等的实数根 D．无法判断【练习 1】关于x的一元二次方程2x2+5x﹣1＝0根的说法，正确的是（）A．方程没有实数根 B．方程有两个相等实数根C．方程有两个不相等实数根 D．方程有一个实数根【练习 2】已知关于x 的不等式组{x −m ＞07−2x ＞1无解，且关于y 的一元二次方程my 2+4y+1＝0有两个不相等的实数根，则整数m 为 ．【练习 3】对于一元二次方程ax 2+bx+c ＝0（a ≠0），有下列说法：①若a+b+c ＝0，则b2﹣4ac ≥0；②若方程ax 2+c ＝0有两个不相等的实根，则方程ax 2+bx+c ＝0必有两个不相等的实根；③若c 是方程ax 2+bx+c ＝0的一个根，则一定有ac+b+1＝0成立；④若x 0是一元二次方程ax 2+bx+c ＝0的根，则b 2﹣4ac ＝（2ax 0+b ）2，其中说法正确的有 ．（填序号）【例2】关于x 的一元二次方程ax 2﹣2x+2＝0有两个不相等实数根，则a 的值可以（ ） A ．1B ．12C ．0D ．﹣1【变式1】关于x 的一元二次方程（a+2）x 2﹣3x+1＝0有实数根，则a 的取值范围（ ） A ．a ≤14且a ≠﹣2B ．a ≤14C ．a ＜14且a ≠﹣2D ．a ＜14【变式2】方程kx 2﹣6x+1＝0有实数根，则k 的取值范围是（ ） A ．k ≤9B ．k ≤9且≠0C ．k ≠0D ．k ＞9【变式3】关于x 的方程kx 2+√k +1x+2＝0有实根，则k 的取值范围是 ． 【变式4】关于x 的方程x 2+bx+c ＝0有两个相等的实数根，x 取m 和m+2时，代数式x 2+bx+c 的值都等于n ，则n ＝ ．【练习1】关于x 的一元二次方程ax 2﹣2x+2＝0有两个相等的实数根，则a 的值为 ．【练习2】已知关于x 的一元二次方程5x 2+2x+m ＝0有实数根，则m 的取值范围是 ． 【练习3】关于x 的方程（k ﹣1）2x 2+（2k+1）x+1＝0有实数根，则k 的取值范围是（ ） A ．k ＞14且k ≠1B ．k ≥14且k ≠1C ．k ＞14D ．k ≥14【例3】关于x 的一元二次方程x 2+（2m ﹣1）x+m 2﹣1＝0有两个不相等的实数根 （1）求m 的取值范围；（2）若m 是满足条件的最大整数，求方程的根．【变式1】已知关于x的一元二次方程x2﹣mx﹣2＝0（1）若x＝﹣1是这个方程的一个根，求m的值和方程的另一根；（2）对于任意的实数m，判断方程的根的情况，并说明理由．【变式2】已知关于x的一元二次方程x2﹣（k+2）x+2k＝0．（1）若x＝1是这个方程的一个根，求k的值和它的另一根；（2）求证：无论k取任何实数，方程总有实数根．（3）若等腰三角形的一边长为5，另两边长恰好是这个方程的两个根，求这个等腰三角形的周长．【变式3】关于x的一元二次方程x2﹣mx+2m﹣4＝0．（1）求证：方程总有两个实数根；（2）若方程有一个根小于1，求m的取值范围．【变式4】已知：关于x的方程kx2﹣（4k﹣3）x+3k﹣3＝0（1）求证：无论k取何值，方程都有实根；（2）若x＝﹣1是该方程的一个根，求k 的值；（3）若方程的两个实根均为正整数，求k的值（k为整数）．【练习1】已知关于x的方程x2﹣2x+2k﹣1＝0有两个实数根．（1）求k的取值范围；（2）若k为正整数，求此时方程的解．【练习2】已知关于x的方程x2﹣（m+3）x+4m﹣4＝0的两个实数根．（1）求证：无论m取何值，这个方程总有实数根．（2）若等腰三角形ABC的一边长a＝5，另两边b，c的长度恰好是这个方程的两个根，求△ABC的周长．【练习3】关于x的一元二次方程（m﹣1）x2﹣2mx+m+1＝0（1）求证：方程总有两个不相等的实数根．（2）m为何整数时，此方程的两个根都是正整数？（3）若△ABC的两边AB，AC的长是这个方程的两个实数根，第三边BC的长为5，当△ABC是等腰三角形时，求m的值．【知识点2 一元二次方程的根与系数的关系-韦达定理】如果一元二次方程ax 2+bx +c =0(a ≠0)的两个实数根是， 那么，；注意它的使用条件为a ≠0， Δ≥0. 【例1】如果1是方程2x 2+bx ﹣4＝0的一个根，则方程的另一个根是（ ） A ．﹣2B ．2C ．﹣1D ．1【变式1】若一元二次方程x 2﹣x ﹣2＝0的两根为x 1，x 2，则（1+x 1）+x 2（1﹣x 1）＝ ． 【变式2】设x 1，x 2是方程x 2+3x ﹣3＝0的两个实数根，则x 2x 1+x1x 2的值为 ．【变式3】已知a 、b 是方程2x 2+5x+1＝0的两实数根，则式子a √a b+b √b a的值为 ．【练习1】一元二次方程x 2﹣4x+a ＝0的两根之积为2，则常数a 的值（ ） A ．﹣2B ．−12C ．12D ．2【练习2】已知m ，n 是关于x 的一元二次方程x 2﹣3x ﹣2＝0的两个根，则（m ﹣1）（n ﹣1）的值为（ ） A ．2B ．0C ．﹣4D ．﹣5【练习3】一元二次方程x 2+4x+1＝0的两个根是x 1，x 2，则x2x 1−x1x 2的值为 ．（其中x 2＞x 1）【例2】若a 、b 是方程x 2+x ﹣2021＝0的两根，则a 2+2a+b ＝ ．【变式1】一元二次方程x 2﹣3x+1＝0的两个根为x 1，x 2，则x 12+3x 2+x 1x 2+1的值为（ ） A ．10B ．9C ．8D ．7【变式2】设x 1、x 2是方程x 2﹣4x+1＝0的两个根，则x 13+4x 22+x 1﹣1的值为 ． 【练习1】如果方程x 2﹣x ﹣2＝0的两个根为α，β，那么α2+β﹣2αβ的值为（ ） A ．7B ．6C ．﹣2D ．0【练习2】已知α、β是方程x 2﹣x ﹣1＝0的两个实数根，则α4+3β的值是（ ） A ．4B ．4√2C ．5D ．5√221x x ，a b x x -=+21acx x =21【例3】如果m、n是两个不相等的实数，且满足m2﹣m＝3，n2﹣n＝3，那么代数式2n2﹣mn+2m+2023＝．【变式1】已知实数a，b分别满足a2﹣6a+4＝0，b2﹣6b+4＝0，且a≠b，则a2+b2的值为（）A．36 B．50 C．28 D．25【变式2】已知a2﹣2a﹣1＝0，b2+2b﹣1＝0，且ab≠1，则ab+b+1b的值为．【变式3】已知实数α，β满足α2+3α﹣1＝0，β2﹣3β﹣1＝0，且αβ≠1，则1α2+3β的值为．【例4】已知：关于x的一元二次方程x2+√m x+m﹣3＝0有两个实数根．（1）求m的取值范围；（2）设方程的两根为x1，x2，且满足x12+x22＝5，求m的值．【变式1】已知关于x的一元二次方程x2﹣（2k+1）x+k2+2k＝0有两个实数根为x1，x2，使得x1x2﹣x12﹣x22＝﹣16成立，则k的值．【变式2】关于x的一元二次方程x2﹣2x+m＝0的二根为x1，x2，且x12﹣x1+x2＝3x1x2，则m ＝．【变式3】已知α、β是关于x的一元二次方程x2+（2m+3）x+m2＝0的两个不相等的实数根．（1）试确定m的取值范围；（2）当1α+1β=−1时，求m的值．【变式4】已知关于x的方程x2+（m+2）x+2m﹣1＝0（1）求证：无论m取任何实数，方程总有两个不相等的实数根；（2）若方程的两个实数根x1，x2满足x1﹣x2＝2，求m的值．=0的两个实数根为α和β，若【练习1】已知二次方程x2+（2m+1）x+m2﹣2m+32|α|+|β|＝4，求m的值．【练习2】已知关于x的一元二次方程x2+（2k+1）x+k2﹣2＝0的两根x1和x2，且x12﹣2x1+2x2＝x1x2，则k的值是．【练习3】已知关于x的一元二次方程x2﹣（2m+4）x+m2+4m＝0．（1）求证：无论m取何值，此方程总有两个不相等的实数根．（2）设方程的两个实数根分别为x1，x2；①求代数式x12+x22−4x1x2的最大值；②若方程的一个根是6，x1和x2是一个等腰三角形的两条边，求等腰三角形的周长．【例5】定义新运算“a*b”：对于任意实数a，b，都有a*b＝a2+b2﹣2ab﹣2，其中等式右边是通常的加法、减法、乘法运算，例如：5*6＝52+62﹣2×5×6﹣2＝﹣1．若方程x*k ＝xk（k为实数）是关于x的方程，则方程的根的情况为（）A．只有一个实数根 B．有两个相等的实数根C．有两个不相等的实数根 D．没有实数根【变式1】对于实数m、n，定义一种运算：m△n＝mn+n．（1）求﹣2△√32得值；有两个相等的实数根，求实数a的值．（2）如果关于x的方程x△（a△x）=−14【变式2】如果关于x 的一元二次方程ax 2+bx+c ＝0有两个实数根x 1，x 2，且满足数轴上x 1，x 2所表示的点到2所表示的点的距离相等，则称这样的方程为“关于2的等距方程”以下“关于2的等距方程”的说法，正确的有 ．（填序号） ①方程x 2﹣4x ＝0是关于2的等距方程；②当5m ＝﹣n 时，关于x 的方程（x+1）（mx+n ）＝0一定是关于2的等距方程； ③若方程ax 2+bx+c ＝0是关于2的等距方程，则必有b ＝﹣4a （a ≠0）； ④当两根满足x 1＝3x 2，关于x 的方程px 2﹣x +34=0是关于2的等距方程．【变式3】如果关于x 的一元二次方程ax 2+bx+c ＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，研究发现了此类方程的一般性结论，设其中一根为t ，则另一根为2t ，因此ax 2+bx+c ＝a （x ﹣t ）（x ﹣2t ）＝ax 2﹣3atx+2t 2a ，所以有b 2−92ac ＝0；我们记“K ＝b 2−92ac ”，即K ＝0时，方程ax 2+bx+c ＝0为倍根方程：下面我们根据所获信息来解决问题：（1）以下为倍根方程的是 ；（写出序号） ①方程x 2﹣x ﹣2＝0；②x 2﹣6x+8＝0；（2）若关于的x 方程mx 2+（n ﹣2m ）x ﹣2n ＝0是倍根方程，求4m 2+5mn+n 2的值； （3）若A （m ，n ）在一次函数y ＝3x ﹣8的图象上，且关于x 的一元二次方程x 2−√mx +23n ＝0是倍根方程，求此倍根方程．【课后练习】1．关于x的一元二次方程x2+4x+2＝0根的情况是（）A．没有实数根 B．有两个不相等的实数根C．只有一个实数根 D．有两个相等的实数根2．若方程x2+3x+c＝0没有实数根，则c的取值范围是（）A．c＜94B．c＜49C．c＞49D．c＞943．关于x的一元二次方程﹣kx2﹣6x+3＝0有两个不相等的实数根，则k的取值范围是（）A．k＞﹣3 B．k＜3 C．k＜3且k≠0 D．k＞﹣3且k≠0 4．已知x1，x2是一元二次方程x2﹣2x＝0的两个实数根，下列结论正确的是（）A．x1+x2＝﹣2 B．x1•x2＝0 C．x1+x2＝0 D．x1•x2＝﹣2 5．设x1，x2是一元二次方程x2﹣3x+2＝0的两个实数根，则x1﹣x1x2+x2的值为．6．已知a，b是方程x2+x﹣1＝0的两个实数根，则a2﹣b+2023的值是（）A．2025 B．2024 C．2023 D．20227．已知关于x的方程2x2+（m+2）x+m＝0；（1）证明：方程总有实数根；（2）若方程有一个根大于1，求m的范围．8．已知关于x的一元二次方程mx2﹣（m+2）x+m4=0有两个不相等的实数根x1，x2．（1）求m的取值范围；（2）若1x1+1x2=4m，求m的值．。

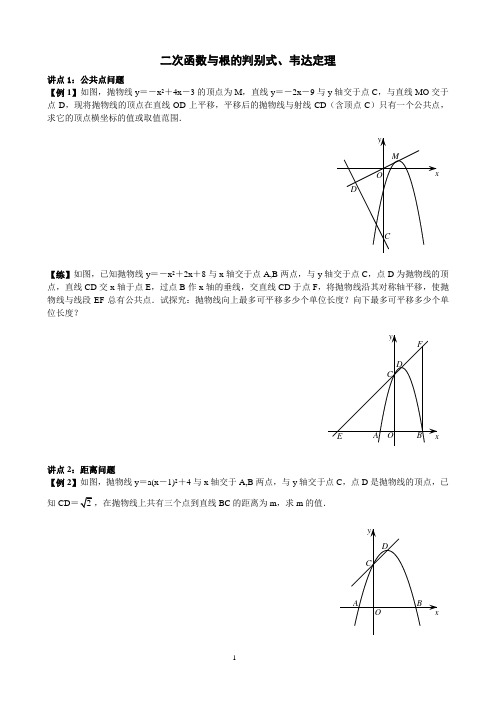
二次函数与根的判别式、韦达定理讲点1：公共点问题【例1】如图，抛物线y ＝－x 2＋4x －3的顶点为M ，直线y ＝－2x －9与y 轴交于点C ，与直线MO 交于点D ，现将抛物线的顶点在直线OD 上平移，平移后的抛物线与射线CD （含顶点C ）只有一个公共点，求它的顶点横坐标的值或取值范围．CO DM yx【练】如图，已知抛物线y ＝－x 2＋2x ＋8与x 轴交于点A,B 两点，与y 轴交于点C ，点D 为抛物线的顶点，直线CD 交x 轴于点E ，过点B 作x 轴的垂线，交直线CD 于点F ，将抛物线沿其对称轴平移，使抛物线与线段EF 总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？FD CE A B O y x讲点2：距离问题【例2】如图，抛物线y ＝a(x －1)2＋4与x 轴交于A,B 两点，与y 轴交于点C ，点D 是抛物线的顶点，已知CD ＝2，在抛物线上共有三个点到直线BC 的距离为m ，求m 的值．CD BAOyx【练】如图，抛物线y ＝ax 2－6ax ＋5a 与x 轴交于A,B 两点（A 左，B 右），若抛物线与直线y ＝2x 的最近点之间的距离为255，求a 的值． yxO B A讲点3：隐藏判别式【例3】如图，点P 是直线l ：y ＝－2x －2上的点，过点P 的另一条直线m 交抛物线y ＝x 2与A,B 两点，试证明：对于直线l 上任意给定的一点P ，在抛物线上都能找到点A ，使得PA ＝AB 成立．PBAO yx【练】如图，已知二次函数y ＝a(x 2－6x ＋8)（a ＞0）的图象与x 轴分别交于点A,B ，与y 轴交于点C ，点D 是抛物线的顶点．当点P 在抛物线对称轴上时，设点P 的纵坐标t 是大于3的常数，试问：是否存在一个正数a ，使得四条线段PA,PB,PC,PD 与一个平行四边形的四条边对应相等（即这四条线段能构成平行四边形）？请说明理由．CPDB AO y x讲点4：交点间的距离【例4】已知二次函数y ＝x 2－2mx ＋m 2＋m 的图象与函数y ＝kx ＋1的图象交于A （x 1，y 1），B （x 2，y 2）（x 1＜x 2）两点．（1）如图1，当k ＝1，m 取不同值时，猜想AB 的长是否不变？并证明你的猜想；A BxOy（2）如图2，当m ＝0，k 取不同值时，猜想△AOB 的形状，并证明你的猜想．BAyOx【例5】如图，抛物线y ＝x 2－4x ＋5与y 轴交于点C ，过点N （1，2）作直线l ，交抛物线于点P ，交y 轴于点E ，连接PC ，若PE ＝PC ，求直线l 的解析式．lE P CN Oy x【练】如图，抛物线C 1：y ＝x 2＋4x ＋3交x 轴于A,B 两点，交y 轴于点C ，将抛物线C 1沿y 轴翻折得新抛物线C 2，过点C 作直线l 交抛物线C 1于点M ，交抛物线C 2于点N ，若MN ＝82，求直线l 的解析式．A B xyO C三、对称问题【例6】如图，已知抛物线y ＝x 2－2x －3，直线y ＝kx －1与抛物线交于P,Q 两点，且y 轴平分线段PQ ，求k 的值．QPO y x【练】如图，已知抛物线y ＝x 2－4x ＋3，过点D （0，－52）的直线与抛物线交于点M,N ，与x 轴交于点E ，且点M,N 关于点E 对称，求直线MN 的解析式．yxNEMD O四、与面积结合【例7】如图，抛物线y ＝x 2－4x ＋5顶点为M ，平移直线y ＝x 交抛物线于点H,K ，若S △MHK ＝3，求平移后直线的解析式．【课后反馈】1．如图，已知抛物线y ＝x 2－2x －3与x 轴交于A,B 两点，与y 轴交于点C ，将抛物线沿对称轴向上平移k 个单位长度后与线段BC 交于D,E 两个不同的点，求k 的取值范围．E C DB A O yx2．如图，抛物线y ＝ax 2－6ax ＋5a 与x 轴交于A,B 两点（A 左，B 右），若抛物线不通过直线y ＝2x 上方的点，求抛物线顶点纵坐标的取值范围．yxO B A3．如图，抛物线y ＝14x 2＋32x ＋2与x 轴交于A,B 两点（点A 在点B 的左边），与y 轴交于点C ，将抛物线沿直线BC 平移，与射线AC （含点A ）仅有一个公共点，求抛物线顶点横坐标的值或取值范围．CBAOyx4．如图，已知抛物线C ：y ＝x 2－2x ＋4和直线l ：y ＝－2x ＋8，直线y ＝kx （k ＞0）与抛物线C 交于A,B 两点，与直线l 交于点P ，分别过A,B,P 作x 轴的垂线，垂足依次为A 1、B 1、P 1，若11OA ＋11OB ＝1u OP ，求u 的值．A 1B 1P 1B AP O yx5．如图1，抛物线C 1：y ＝x 2＋4x ＋3顶点为M ，抛物线C 2与抛物线C 1开口方向相反，形状相同，顶点为N ，且M,N 关于点P （0，2）对称． （1）求抛物线C 2的解析式；N MPOyx（2）直线y ＝m 交抛物线C 1于点A,B ，交抛物线C 2于点C,D ，若AB ＝2CD ，求m 的值；DCB ANMOyx。

一元二次方程根与系数的关系应用例析及训练对于一元二次方程ax?+bx+c = 0(a式0)，当判别式心= b?_4ac兰0时，其求根公式为：％、=―' b——4ac；当2ab c.：_0时，设一元二次方程的两根为X「x2，有：x-i x2，x-i x2;根与系数的这种关系又称为韦达定理；它的a ab c逆定理也是成立的，即当x-i x2，x-i x2时，那么为、x2则是方程ax2bx c = 0(a = 0)的两根。

一元二次方程a a的根与系数的关系，综合性强，应用极为广泛，在中学数学中占有极重要的地位，也是数学学习中的重点。

学习中，除了要求熟记一元二次方程ax2 bx c =0(a =0)根的判别式厶二b2 -4ac存在的三种情况外，还常常要求应用韦达定理解答一些变式题目，以及应用求根公式求出方程ax2 bx 0(^- 0)的两个根为、x2，进而分解因式，即ax2bx • c = a(x-xj(x-x2)。

下面就对韦达定理的应用可能出现的问题举例做些分析，希望能带来小小的帮助。

一、根据判别式，讨论一元二次方程的根。

例1：已知关于x的方程(1) X2 -(1-2a)x • a2 -3 =0有两个不相等的实数根，且关于x的方程⑵x2-2x，2a-1=：0没有实数根，问a取什么整数时，方程(1)有整数解？分析：在同时满足方程(1)，(2)条件的a的取值范围中筛选符合条件的a的整数值。

解：a的取值范围，并依靠熟练的解不等式的基本技说明：熟悉一元二次方程实数根存在条件是解答此题的基础，正确确定能和一定的逻辑推理，从而筛选出a,这是解答本题的基本技巧。

二、判别一元二次方程两根的符号。

例2：不解方程，判别方程2x2・3x-7=0两根的符号。

判别根的符号，需要把“根的判别式”和“根与系数的关系”结合起来进行确定，倘若由题中x1 x^：： 0，所以可判定方程的根为一正一负；倘若为x2 0，仍需考虑x1 X2的正负，倘若x1 x2 • 0，则方程有两个正数根；倘若x1 X2：：：0，则方程有两个负数根。

初中数学培优：韦达定理与根的判别式一、利用根的判别式求字母的取值范围【典例】已知方程x2﹣2|x|﹣15＝0，则此方程的所有实数根的和为（）A．0B．﹣2C．2D．8【解答】解：①当x＞0时，方程化为：x2﹣2x﹣15＝0，即（x+3）（x﹣5）＝0，∴x+3＝0，x﹣5＝0，解得x1＝﹣3（舍去），x2＝5，②当x＜0时，方程化为：x2+2x﹣15＝0，即（x﹣3）（x+5）＝0，∴x﹣3＝0，x+5＝0，解得x3＝3（舍去），x4＝﹣5，③当x＝0时，方程不成立．∴此方程的所有实数根的和为：5+（﹣5）＝0．或原方程可化为：（|x|﹣5）（|x|+3）＝0，即|x|﹣5＝0，|x|+3＝0，∴|x|＝5，|x|＝﹣3（舍去），解得x＝5或﹣5，∴此方程的所有实数根的和为：5+（﹣5）＝0．故选：A．【巩固】关于x的一元二次方程x2+（2m+1）x+m2﹣1＝0有两个不相等的实数根．（1）求m的取值范围；（2）若m为不大于1的整数，且方程的根为整数，求满足条件的m的值及对应的方程的根．【解答】解：（1）∵关于x的一元二次方程x2+（2m+1）x+m2﹣1＝0有两个不相等的实数根，∴b2﹣4ac＝（2m+1）2﹣4（m2﹣1）＝4m+5＞0，解得：m＞−54，即m的取值范围是m＞−54；（2）由（1）知：当m＞−54时，方程有两个不相等的实数根，∵m为不大于1的整数，∴m＝0，﹣1，1，又m＝0时，方程x2+x﹣1＝0的根不是整数，当m＝﹣1时，则方程为x2﹣x＝0，解得：x1＝1，x2＝0，即当m＝﹣1时，方程的解是x1＝1，x2＝0．当m＝1时，则方程为x2+3x＝0，解得：x1＝﹣3，x2＝0，即当m＝1时，方程的解是x1＝﹣3，x2＝0．二、利用根的判别式求最值【典例】满足（x﹣3）2+（y﹣3）2＝6的所有实数对（x，y）中，的最大值是多少？【解答】解：设y＝kx，则直线y＝kx与圆（x﹣3）2+（y﹣3）2＝6相切时k有最大值和最小值，把y＝kx代入（x﹣3）2+（y﹣3）2＝6，得（1+k2）x2﹣6（k+1）x+12＝0，∴Δ＝36（k+1）2﹣4×12×（1+k2）＝0，即k2﹣6k+1＝0，解此方程得，k＝3+22或3﹣22．所以=k的最大值是3+22．【巩固】阅读下面的材料，并解答问题：分式2r8r2(≥0)的最大值是多少？解：2r8r2=2r4+4r2=2(r2)+4r2=2+4r2，因为x≥0，所以x+2的最小值是2，所以4r2的最大值是2，所以2+4r2的最大值是4，即2r8r2(≥0)的最大值是4．根据上述方法，试求分式22+102+2的最大值是．【解答】解：22+102+2=22+4+62+2=2(2+2)+62+2=2+62+2，∵x2≥0，∴x2+2的最小值为2，∴62+2的最大值为3，∴2+62+2的最大值为5，∴分式22+102+2的最大值是5，故答案为：5．三、韦达定理与根的判别式综合【典例】若关于x的一元二次方程（m﹣4）x2+（2m﹣1）x+1＝0的两个实数根的倒数和为s，则s的取值范围是．【解答】解：根据题意得m﹣4≠0且Δ＝（2m﹣1）2﹣4（m﹣4）≥0，解得m≠4，x1+x2=−2K1K4，x1x2=1K4，s=11+12=1+212=−2m+1，由于m≠4，所以s≠﹣7．故答案为s≠﹣7．【巩固】已知关于x的一元二次方程2x2﹣4mx+2m2+3m﹣2＝0有两个实数根．（1）求实数m的取值范围；（2）设x1，x2是原方程的两个实数根，当m为何值时，x12+x22有最小值？并求这个最小值．【解答】解：（1）∵一元二次方程2x2﹣4mx+2m2+3m﹣2＝0有两个实数根，∴b2﹣4ac＝（﹣4m）2﹣4×2（2m2+3m﹣2）≥0，∴﹣24m+16≥0，∴m≤23，∴实数m的取值范围为≤23；（2）∵x1+x2＝2m，x1•x2=12（2m2+3m﹣2），∴x12+x22＝（x1+x2）2﹣2x1x2＝（2m）2﹣2×12（2m2+3m﹣2）＝2m2﹣3m+2＝2（m−34）2+78，∵m≤23，23＜34，∴当m=23时，x12+x22＝2（23−34）2+78=89，∴当m=23时，x12+x22有最小值，最小值是89．巩固练习1．如果方程（x﹣1）（x2﹣2x+m）＝0的三根可作为一个三角形的三边之长，则实数m的取值范围是（）A．0≤m≤1B．34≤m C．34≤m≤1D．34＜m≤1【解答】解：∵方程（x﹣1）（x2﹣2x+m）＝0有三根，∴x1＝1，x2﹣2x+m＝0有根，方程x2﹣2x+m＝0的Δ＝4﹣4m≥0，得m≤1．又∵原方程有三根，且为三角形的三边和长．∴有x2+x3＞x1＝1，|x2﹣x3|＜x1＝1，而x2+x3＝2＞1已成立；当|x2﹣x3|＜1时，两边平方得：（x2+x3）2﹣4x2x3＜1．即：4﹣4m＜1．解得m＞34．∴34＜m≤1．故选：D．2．关于x的方程（k﹣1）2x2+（2k+1）x+1＝0有实数根，则k的取值范围是（）A．k＞14且k≠1B．k≥14且k≠1C．k＞14D．k≥14【解答】解：当k﹣1≠0，即k≠1时，此方程为一元二次方程．∵关于x的方程（k﹣1）2x2+（2k+1）x+1＝0有实数根，∴Δ＝（2k+1）2﹣4×（k﹣1）2×1＝12k﹣3≥0，解得k≥14；当k﹣1＝0，即k＝1时，方程为3x+1＝0，显然有解；综上，k的取值范围是k≥14，故选：D．3．已知m，n是方程x2−5x+1＝0的两个根．记S1=11++11+，S2=11+2+11+2，…，S t=11++ 11+（t为正整数）．若S1+S2+…S t＝t2﹣56，则t的值为（）A．7B．8C．9D．10【解答】解：∵m，n是方程x2−5x+1＝0的两个根，∴m+n=5，mn＝1，∴S1=11++11+=1+r1+(1+p(1+p=2+(rp=＝1，S2=11+2+11+2=1+2+1+2(1+2)(1+2)=2+(rp2−2B1+(rp2−2B+(B)2=2+5−21+5−2+1＝1，…，∴S t=11++11+=1，∴S1+S2+…S t＝t2﹣56，1+1+…+1＝t2﹣56，t＝t2﹣56，t 2﹣t ﹣56＝0，（t ﹣8）（t +7）＝0，解得：t ＝8或t ＝﹣7（舍去）．故选：B ．4．若关于x 的一元二次方程12x 2﹣2mx ﹣4m +1＝0有两个相等的实数根，则（m ﹣2）2﹣2m （m ﹣1）的值为．【解答】解：由题意可知：Δ＝4m 2﹣2（1﹣4m ）＝4m 2+8m ﹣2＝0，∴m 2+2m =12，∴（m ﹣2）2﹣2m （m ﹣1）＝﹣m 2﹣2m +4=−12+4=72，故答案为：725．设下列三个一元二次方程：x 2+4ax ﹣4a +3＝0；x 2+（a ﹣1）x +1+a 2＝0；x 2+2ax ﹣2a +3＝0，至少有一个方程有实根，则实数a 的取值范围是．【解答】解：不妨假设三个方程都没有实数根，则有162+16−12＜0(−1)2−4(2+1)＜042−4(3−2p ＜0，解得−32＜a ＜12．故答案为：a ≤−32或a ≥12．6．已知关于x 的一元二次方程（1﹣2k ）x 2﹣2+3x ﹣1＝0有两个不相等的实数根，则k 的取值范围．【解答】解：∵关于x 的一元二次方程（1﹣2k ）x 2﹣2+3x ﹣1＝0有两个不相等的实数根，∴1−2≠0+3≥0△=(−2+3)2−4(1−2p ×(−1)＞0，解得：﹣3≤k ＜4且k ≠12．故答案为：﹣3≤k ＜4且k ≠12．7．关于x 的一元二次方程x 2+ax ﹣1＝0的两个根分别为m 、n ，则（x +1）2+a （x +1）﹣1＝0的根为．【解答】解：∵关于x 的一元二次方程x 2+ax ﹣1＝0的两个根分别为m 、n ，∴m 2+am ﹣1＝0，n 2+an ﹣1＝0，设x+1＝m或n，则（x+1）2+a（x+1）﹣1＝0，∴（x+1）2+a（x+1）﹣1＝0的根为x＝m﹣1或n﹣1，故答案为：x＝m﹣1或n﹣1．8．已知实数x，y满足（2x+1）2+y2+（y﹣2x）2=13，求x+y的值．【解答】解：由（2x+1）2+y2+（y﹣2x）2=13，得（3x+1）2+3（x﹣y）2＝0，则3+1=0−=0，解得=−13=−13，故x+y=−13−13=−23．9．已知关于x的一元二次方程（a+b）x2+2cx+（b﹣a）＝0，其中a、b、c分别为△ABC三边的长．（1）如果x＝﹣1是方程的根，试判断△ABC的形状，并说明理由；（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；（3）如果△ABC是等边三角形，试求这个一元二次方程的根．【解答】解：（1）△ABC是等腰三角形，理由：当x＝﹣1时，（a+b）﹣2c+（b﹣a）＝0，∴b＝c，∴△ABC是等腰三角形，（2）△ABC是直角三角形，理由：∵方程有两个相等的实数根，∴Δ＝（2c）2﹣4（a+b）（b﹣a）＝0，∴a2+c2＝b2，∴△ABC是直角三角形；（3）∵△ABC是等边三角形，∴a＝b＝c，∴原方程可化为：2ax2+2ax＝0，即：x2+x＝0，∴x（x+1）＝0，∴x1＝0，x2＝﹣1，即：这个一元二次方程的根为x1＝0，x2＝﹣1．10．如果关于x的一元二次方程ax2+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，研究发现了此类方程的一般性结论：设其中一根为t，则另一个根为2t，因此ax2+bx+c＝a（x﹣t）（x﹣2t）＝ax2﹣3atx+2t2a，所以有b2−92ac＝0；我们记“K＝b2−92ac”即K＝0时，方程ax2+bx+c＝0为倍根方程；下面我们根据此结论来解决问题：（1）方程①x2﹣x﹣2＝0；方程②x2﹣6x+8＝0这两个方程中，是倍根方程的是（填序号即可）；（2）若（x﹣2）（mx+n）＝0是倍根方程，求4m2+5mn+n2的值；（3）关于x的一元二次方程x2−B+23n＝0（m≥0）是倍根方程，且点A（m，n）在一次函数y＝3x﹣8的图象上，求此倍根方程的表达式．【解答】解：（1）在方程①x2﹣x﹣2＝0中，K＝（﹣1）2−92×1×（﹣2）＝10≠0；在方程②x2﹣6x+8＝0中，K＝（﹣6）2−92×1×8＝0．∴是倍根方程的是②x2﹣6x+8＝0．故答案为：②．（2）整理（x﹣2）（mx+n）＝0得：mx2+（n﹣2m）x﹣2n＝0，∵（x﹣2）（mx+n）＝0是倍根方程，∴K＝（n﹣2m）2−92m•（﹣2n）＝0，∴4m2+5mn+n2＝0．（3）∵2−B+23=0是倍根方程，∴=(−p2−92×23=0，整理得：m＝3n．∵A（m，n）在一次函数y＝3x﹣8的图象上，∴n＝3m﹣8，∴n＝1，m＝3，∴此方程的表达式为2−3+23=0．11．设m是不小于﹣1的实数，关于x的方程x2+2（m﹣2）x+m2﹣3m+3＝0有两个不相等的实数根x1、x2，（1）若x12+x22＝6，求m值；（2）求B121−1+B221−2的最大值．【解答】解：∵方程有两个不相等的实数根，∴Δ＝b2﹣4ac＝4（m﹣2）2﹣4（m2﹣3m+3）＝﹣4m+4＞0，∴m＜1，结合题意知：﹣1≤m ＜1．（1）∵x 12+x 22＝（x 1+x 2）2﹣2x 1x 2＝4（m ﹣2）2﹣2（m 2﹣3m +3）＝2m 2﹣10m +10＝6∴=∵﹣1≤m ＜1，∴=（2）B 121−1+B 221−2=n 12+22−12(1+2)](1−1)(1−2)=o23−82+8K2)2−=2oK1)(2−3r1)oK1)=2(2−3+1)=2(−32)2−52（﹣1≤m ＜1）．∵对称轴m =32，2＞0，∴当m ＝﹣1时，式子取最大值为10．12．如果方程x 2+px +q ＝0的两个根是x 1，x 2，那么x 1+x 2＝﹣p ，x 1•x 2＝q ，请根据以上结论，解决下列问题：（1）若p ＝﹣4，q ＝3，求方程x 2+px +q ＝0的两根．（2）已知实数a 、b 满足a 2﹣15a ﹣5＝0，b 2﹣15b ﹣5＝0，求+的值；（3）已知关于x 的方程x 2+mx +n ＝0，（n ≠0），求出一个一元二次方程，使它的两个根分别是已知方程两根的倒数．【解答】解：（1）当p ＝﹣4，q ＝3，则方程为x 2﹣4x +3＝0，解得：x 1＝3，x 2＝1．（2）∵a 、b 满足a 2﹣15a ﹣5＝0，b 2﹣15b ﹣5＝0，∴a 、b 是x 2﹣15x ﹣5＝0的解，当a ≠b 时，a +b ＝15，ab ＝﹣5，+=2+2B=(rp 2−2BB=152−2×(−5)−5=−47；当a ＝b 时，原式＝2．（3）设方程x 2+mx +n ＝0，（n ≠0），的两个根分别是x 1，x 2，则11+12=1+212=−，11•12=112=1，则方程x 2+x +1=0的两个根分别是已知方程两根的倒数．。

一元二次方程根的判别式及韦达定理常见题型及注意事项一、一元二次方程跟的判别式的常见题型题型1：不解方程，判断一元二次方程根的情况题型2：证明一元二次方程根的情况求证：无论k 取何实数，关于x 的一元二次方程：2(1)40x k x k -++-=总有两个不等实根。

题型3：已知一元二次方程根的情况．．，求方程中未知系数的取值范围 1．（ 2011·重庆）已知关于x 的一元二次方程．．．．．．(a －1)x 2－2x +1=0有两个不相等的．．．．．．实数根,则a 的取值范围是( )A.a <2 B,a >2 C.a <2且a ≠1 D.a <－2·变式1：（2010·安徽芜湖）关于x 的方程．．(a －5)x 2－4x －1＝0有实数根．．．．，则a 满足（） A ．a ≥1 B ．a ＞1且a ≠5 C ．a ≥1且a ≠5 D ．a ≠5 注意：要特别注意二次项系数是否为0，即原方程是否“一定为一元二次方程”。

变式2：（2010 ·成都）若关于x 的一元二次方程2420x x k ++=有两个实数根，求k 的取值范围及k 的非负整数．．．．值. 变式3：已知关于x 的一元二次方程(12)10k x k x ---=有两个实数根，求k 的取值范围 二、一元二次方程根与系数的关系------韦达定理的常见题型题型1：已知一元二次方程的一根，求另一根及未知系数k 的值已知23-是方程210x kx ++=的一根，则方程的另一根是 ，k = 。

题型2：求与一元二次方程根有关的代数式的值；1. 已知12,x x 是方程22430x x --=的两根，计算： （1）2212x x +； ⑵ 1211x x +；⑶212()x x - 变式：已知,a b 是方程2201230x x -+=的两实根，求22(20103)(20103)a a b b -+-+的值题型3：已知一元二次方程两根的关系．．．．．，求方程中未知系数的取值 1． 关于x 的一元二次方程22(21)10x k x k +-+-=的两个实根的平方和等于9，求k 的值 变式1： （2011·荆州）关于x 的方程0)1(2)13(2=+++-a x a ax 有两个不相等的实根1x 、2x ，且有a x x x x -=+-12211，则a 的值是（ ）A ．1B ．－1C ．1或－1D ． 2 注意：要特别注意应用韦达定理的前提条件是原方程有实根，即原方程：△≥0。