《用函数的观点看方程(组)或不等式》一次函数PPT课件

【本讲主要内容】用函数观点看方程（组）与不等式1. 一次函数与一元一次方程的关系2. 一次函数与一元一次不等式的关系3. 一次函数与二元一次方程（组）的关系【知识掌握】【知识点精析】一. 一次函数与一元一次方程的关系由于任何一元一次方程都可以转化为ax b+=0（a b、是常数，a≠0）的形式，所以解一元一次方程可以转化为：当某个一次函数的值为0时，求相应的自变量的值．从图象上看这相当于已知直线y ax b=+，确定它与x轴交点的横坐标的值．二. 一次函数与一元一次不等式的关系由于任何一元一次不等式都可以转化为ax b+>0或ax b+<0（a b、是常数，a≠0）的形式，所以解一元一次不等式可以看作：当一次函数值大（小）于0时，求自变量相应的取值范围．从图象上看，解ax b+>0相当于已知直线y ax b=+在x轴上方时，自变量x 相应的取值范围；解ax b+<0相当于已知直线y ax b=+在x轴下方时，自变量x相应的取值范围．三. 一次函数与二元一次方程（组）的关系每个二元一次方程组都对应两个一次函数，于是也对应两条直线．从“数”的角度看，解方程组相当于考虑自变量为何值时两个函数的值相等，以及这个函数值是何值；从“形”的角度看，解方程组相当于确定两条直线交点的坐标．方程（组）、不等式与函数之间互相联系，用函数观点可以把它们统一起来，解决问题时，应根据具体情况灵活地、有机地把它们结合起来使用．【解题方法指导】例1. （2006年重庆市中考题）（课改实验区考生做）如图，已知函数y ax b y kx=+=和的图像交于点P，则根据图像可得，关于x y、的二元一次方程组y ax by kx=+=⎧⎨⎩的解是______．∴l2的函数表达式为y x=-10075（2）乙车先到达B地．3001007515 4=-∴=x x，设l1的函数表达式是y k x=1O图像过点()154300，∴k 1=80．即y x =80当y =400时，400805=∴=x x ， ∴-=519414（小时）键性词语；三要有一定的生产、生活常识，对当前市场经济条件下各种常见的现象有所了解，能抓住它们的本质和规律，恰当地构建出数学模型．【典型例题分析】例1. （2006年云南省课改实验区中考题）如图，直线l l 12与相交于点P ，l 1的函数表达式为y x =+23，点P 的横坐标为-1，且l 2交y 轴于点A （0，-1）．求直线l 2的函数表达式．若x y ==23，，则0621342..⨯+⨯=（万元）∴电视台选择15秒广告播放4次、30秒广告播放2次的方式，收益较大． 点评：本题综合应用了二元一次方程与一次函数的知识解决实际问题．例3. （2006年浙江省中考题）宁波市土地利用现状通过国土资源部验收，我市在节约集约用地方面已走在全国前列．1996~2004年，市区建设用地总量从33万亩增加到48万亩，相应的年GDP从295亿元增加到985亿元．宁波市区年GDP y（亿元）与建设用地总量x（万亩）之间存在着如图所示的一次函数关系．（1）求y关于x的函数关系式．（2）据调查2005年市区建设用地比2004年增加4万亩，如果这些土地按以上函数关系式开发使用，那么2005年市区可以新增GDP多少亿元？（3）按以上函数关系式，我市年GDP每增加1亿元，需增建设用地多少万亩？（精确到0.001万亩）∴-=≈x x21460022.（万亩）即年GDP每增加1亿元，需增加建设用地约0.022万亩．例4. （2006年云南省中考题）云南省公路建设发展速度越来越快，通车总里程已位居全国第一，公路的建设促进了广大城乡客运的发展．某市扩建了市县际公路，运输公司根据实际需要计划购买大、中两型客车共10辆，大型客车每辆价格为25万元，中型客车每辆价格为15万元．（1）设购买大型客车x（辆），购车总费用为y（万元），求y与x之间的函数表达式；（2）若购车资金为180万元至200万元（含180万元和200万元），那么有几种购车方案？在确保交通安全的前提下，根据客流量调查，大型客车不能少于4辆，此时如何确定购车方案可使该运输公司购车费用最少？解：（1）设购买大型客车x辆，则购买中型客车()10-x辆．由题意得：y x x=+-251510()，即y x=+10150（2）1015018010150200xx+≥+≤⎧⎨，解得xx≥≤⎧⎨35，∴≤≤35x（山西省课改实验区）如图，是某函数的图象，则下列结论中正确的是（的取值是-325，B. 当y=-3时，x的近似值是0，2C. 当x=-32时，函数值y最大D. 当x>-3时，y随x的增大而增大2. （太原市）小亮用作图象的方法解二元一次方程组时，在同一直角坐标系内作出了相应的两个一次函数的图象l l12、如图所示，他解的这个方程组是（）2xy+-=,2（黄冈市课改实验区）如图，在光明中学学生耐力测试比赛中，甲、乙两学生测试的（秒）之间的函数关系图像分别为折线OABC正确的是（）A. 乙比甲先到达终点B. 乙测试的速度随时间增加而增大C. 比赛进行到29.4秒时，两人出发后第一次相遇D. 比赛全程甲的测试速度始终比乙的测试速度快二. 填空题：某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y （微克）随时间x （小时）的变化情况如图所示，当成人按规定剂量服用后，（1）服药后________小时，血液中含药量最高，达每毫升______毫克，接着逐步衰减； （2）服药5小时，血液中含药量_______毫克；（3）当x ≤2时，y 与x 之间的函数关系式是___________； （4）当x ≥2时，y 与x 之间的函数关系式是___________；（5）如果每毫升血液中含药量3毫克或3毫克以上时，治疗疾病最有效，那么这个有效时间是_________小时．三. （昆明市课改实验区）如图，直线l 1与l 2相交于点P ，l 1的函数表达式为y x =+23，点P 的横坐标为-1，且l 2交y 轴于点A （0，-1）．求直线l 2的函数表达式．四. （河北省课改实验区）甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度y（m）与挖掘时间x（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：（1）乙队开挖到30m时，用了__________h．开挖6h时甲队比乙队多挖了______m；（2）请你求出：①甲队在06x的时段内，y与x之间的函数关系式；≤≤②乙队在26x的时段内，y与x之间的函数关系式；≤≤（3）当x为何值时，甲、乙两队在施工过程中所挖河渠的长度相等？五. （2004年黑龙江省中考题）某送奶公司计划在三栋楼之间建一个取奶站，三栋楼在同一条直线上，顺次为A楼、B楼、C楼，其中A楼与B楼之间的距离为40米，B楼与C楼之间的距离为60米．已知A楼每天有20人取奶，B楼每天有70人取奶，C楼每天有60人取奶，送奶公司提出两种建站方案．方案一：让每天所有取奶的人到奶站的距离总和最小；方案二：让每天A楼与C楼所有取奶的人到奶站的距离之和等于B楼所有取奶的人到奶站的距离之和．（l）若按照方案一建站，取奶站应建在什么位置？（2）若按照方案二建站，取奶站应建在什么位置？（3）在（2）的情况下，若A楼每天取奶的人数增加（增加的人数不超过22人），那么取奶站将离B楼越来越远，还是越来越近？请说明理由．【综合测试答案】一. 选择题：1. B2. D3. C4. C二. 填空题：（1）2，6； （2）3 （3）y x =3（4）y x =-+8 （5）4三. 解：设点P 坐标为（-1，y ），代入y x =+23，得y =∴1,点P （-1，1）设直线l 2的函数表达式为y kx b =+，把P （-1，1）、A （0，-1）分别代入y kx b =+，得11=-+-=⎧⎨⎩k b b∴=-=-⎧⎨⎩k b 21，∴直线l 2的函数表达式为y x =--21．四. 解：（1）2，10；（2分）（2）①设甲队在06≤≤x 的时段内y 与x 之间的函数关系式为y k x =1， 由图可知，函数图像过点（6，60）， ∴=6601k ，解得k y x 11010=∴=,（4分）②设乙队在26≤≤x 的时段内y 与x 之间的函数关系式为y k x b =+2， 由图可知，函数图像过点（2，30），（6，50）， ∴+=+=⎧⎨⎩23065022k b k b ,解得k b 2520==⎧⎨⎩,∴=+y x 520 （6分）（3）由题意，得10520x x =+，解得x h =4()． ∴当x 为4h 时，甲、乙两队所挖的河渠长度相等．五. 解：（1）设取奶站建在距A 楼x 米处，所有取奶的人到奶站的距离总和为y 米， ①当040≤≤x 时，y x x x x =+-+-=-+207040601001108800()()∴当x =40时，y 的最小值为4400②当40100<≤x 时，y x x x x =+-+-=+20704060100303200()()，此时，y 的值大于4400因此按方案一建奶站，取奶站应建在B 楼处 （2）设取奶站建在距A 楼x 米处，①当040≤≤x 时，20601007040x x x +-=-()()解得x =-<32030（舍去）②当40100<≤x 时，20601007040x x x +-=-()()解得x =80 因此按方案二建奶站，取奶站应建在距A 楼80米处 （3）设A 楼取奶人数增加a 人，第11页 版权所有 不得复制 11①当040≤≤x 时，()()()20601007040++-=-a x x x ， 解得x a =-+320030（舍去），②当40100<≤x 时， ()()()20601007040++-=-a x x x 解得x a =-∴8800110,当a 增大时，x 增大，∴当A 楼取奶的人数增加时，按照方案二建奶站，取奶站仍建在B 、C 两楼之间，且随着人数的增加，离B 楼越来越远。

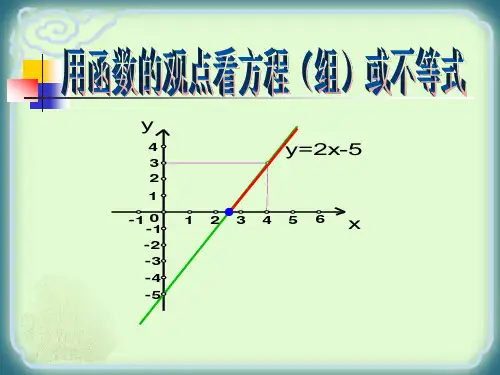
第三节一次函数与方程（组）及一元一次不等式二、核心纲要直线:y = kx+b(k≠0)与x轴交点的横坐标，就是一元一次方程kx+b = 0 (k≠0)的解.求直线y = kx+b与x轴交点时，可令y = 0，得到方程k + B = 0,解方程得x=bk-，直线y=kx+b交x轴于点(bk-,0)，bk-就是直线y =kx+b与x轴交点的横坐标，可令y轴交点的横坐标.注：(1)从“数”看:kx+b=0(k≠0)的解⇔在一次函数y=kx+b(k≠0)中，令y=0时，x的值.(2)从“形”看:kx+b=0(k≠0)的解⇔一次函数y=kx+b(k≠0)的图像与x轴交点的横坐标.2.—次函数与一元一次不等式的关系(1) 任何一次一次不等式都可以转化为ax+b>0或ax + b<0(a，b为常数，a≠0)的形式，所以解一元一次不等式可以看作：当一次函数值大(小）于0时，求自变量相应的取值范围.(2) 函数图像的位置决定两个函数值的大小关系①函数y1的图像在函数y2的图像的上方⇔y1>y2，如下图所示；②函数y1的图像在函数y2的下方⇔y1<y2，如下图所示；③特别说明：函数y 的图像在x 轴上方⇔y >0；函数y 的图像在X 轴下方y <0.3.一次函数与二元一次方程（组）的关系(1)一次函数的解析式：y =kx +b (k ≠0)本身就是一个二元一次方程，直线y =kx +b (k ≠0)上有无数个点，每个点的横纵坐标都满足二元一次方程y =kx +b (k ≠0)，因此二元一次方程的解也就有无数个. (2) —次函数:y = kx +b (k ≠0)① 从“数”看，它是一个二元一次方程； ② 从“形”看，它是一条直线。

4.两条直线的位置关系与二元一次方程组的解 (1) 二元一次方程组1122y k x b y k x b =+⎧⎨=+⎩有唯一的解⇔直线y =k 1x +b 1不平行于直线y =k 2x +b 2⇔k 1≠k 2.(2) 二元一次方程组1122y k x b y k x b =+⎧⎨=+⎩无解⇔直线y =k 1x +b 1平行于直线y =k 2x +b 2⇔k 1=k 2,b 1≠b 2. (3) 二元一次方程组1122y k x b y k x b =+⎧⎨=+⎩有无数多个解⇔直线y =k 1x +b 1与y =k 2x +b 2重合⇔k 1=k 2,b 1=b 2.5.比较两个函数值大小的方法 (1) 画图像，求交点.(2) 过交点作平行于y 轴的直线. (3) 谁高谁大.6.数学思想数形结合和转化思想.本节重点讲解：一个定理，一个证明，两个思想.三、全能突破1.若直线y =(m -3)x +6与x 轴交于点(3,0)，则m 的值为( ) A. 1 B. 2 C. 3 D. 42.如图19-3-1所示，一次函数y =kx +b 的图像经过A 、B 两点，则kx +b ≥0的解集是( ) A. x >0 B. x ≥—3 C. x >2 D. -3≤x ≤23.已知ax +b =0的解是2,则直线y =ax +b 与x 轴的交点坐标是______。

用函数观点看方程与不等式知识梳理1．一元一次方程、一元一次不等式及一次函数的关系一次函数及其图像与一元一次方程及一元一次不等式有着密切的关系，函数y=ax+b （a≠0，a ，b 为常数）中，函数的值等于0时自变量x 的值就是一元一次方程ax+•b=0（a≠0）的解，所对应的坐标（－ba，0）是直线y=ax+b 与x 轴的交点坐标，反过来也成立；•直线y=ax+b 在x 轴的上方，也就是函数的值大于零，x 的值是不等式ax+b>0（a≠0）的解；在x 轴的下方也就是函数的值小于零，x 的值是不等式ax+b<0（a≠0）的解． 2．坐标轴的函数表达式函数关系式x=0的图像是y 轴，反之，y 轴可以用函数关系式x=0表示；•函数关系式y=0的图像是x 轴，反之，x 轴可以用函数关系式y=0表示． 3．一次函数与二元一次方程组的关系一般地，每个二元一次方程组，都对应着两个一次函数，于是也就是对应着两条直线，从“数”的角度看，解方程相当于考虑自变量为何值时两个函数的值相等，以及这两函数值是何值；从形的角度考虑，解方程组相当于确定两条直线的交点坐标，所以一次函数及其图像与二元一次方程组有着密切的联系． 4．两条直线的位置关系与二元一次方程组的解 （1）二元一次方程组1122y k x b y k x b =+⎧⎨=+⎩有唯一的解⇔直线y=k 1x+b 1不平行于直线y=k 2x+b 2 ⇔k 1≠k 2．（2）二元一次方程组1122y k x b y k x b =+⎧⎨=+⎩无解⇔直线y=k 1x+b 1∥直线y=k 2x+b 2 ⇔k 1=k 2，b 1≠b 2．（3）二元一次方程组1122y k x b y k x b =+⎧⎨=+⎩有无数多个解⇔直线y=k 1x+b 1与y=k 2x+b 2重合⇔k 1=k 2，b 1=b 2．5、二次函数与一元二次方程组的关系（1）如果抛物线y ax bx c =++2与x 轴有公共点，公共点的横坐标是x 0，那么当x x =0时，函数的值是0，因此x x =0就是方程ax bx c 20++=的一个根。

用函数观点看方程（组）与不等式
第一课时 一次函数与一元一次方程
学习目标：
1、理解一次函数与一元一次方程的关系；
2、会根据一次函数的图象解决一元一次方程的求解。

学习重点：
用一次函数的图象求解一元一次方程。

学习难点：
一次函数与一元一次方程的关系的发现，归纳和运用。

学习过程：
一、自主学习：
（一）学生看课本P 123，完成下列问题：
（1）方程2x+20=0的解为________。

（2）自变量x 为_________时，函数y=2x+20的值为0？
（3）画出函数y=2x+20的图象，它与x 轴交点的坐标是(_______)。

（4）直线y=2x+20与x 轴交点的横坐标与方程2x+20=0的解有什么关系？
（学生独立思考后可进行小组内讨论、交流，并最终得出结论）。

结论：
求一元一次方程的解就是求一次函数与x 轴交点的横坐标。

（二）看例1，再次验证一次函数与一元一次方程的关系。

二、自主检测：
1、一元一次方程3x-6=0的解为x=2，那么一次函数y=3x-6的函数值为0时，自变量x 的取值为_______。

2、函数y=-21x-3的图象与x
-21x-3=0的解是_________。

3、如图是函数y=2x+2的图象，由图象可知
方程2x+2=0的解是__________。

4、当自变量x 的值满足什么条件时，函数列条件？
（1）y=0 （2）y=-5
三、课堂小结：
本节课你收获了什么？
四、布置作业：
课本P129 1，2
教后感：。